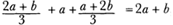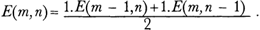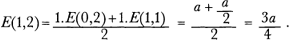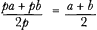De Zeventiende Eeuw. Jaargang 12
(1996)– [tijdschrift] Zeventiende Eeuw, De–
[pagina 171]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Christiaan Huygens' non-probabilistic approach to a calculus of games of chance
| |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 172]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
the proofs of the two most important propositions in Huygens' ‘theory’ are wrong. This has never been noticed before. The failure of Huygens' proofs justifies the assumption that the genesis of Huygens' ‘theory’ of games of chance is independent of the conceptions behind these proofs. Why Huygens superimposed on his ‘theory’ the construction characteristic of his proofs will be discussed below in the last part of this paper, which offers in addition hints for Huygens' connection with an older tradition in treating games of chance.
Amongst all the mathematicians of the 17th century none was more concerned with rigour according to the standards of the great Greek mathematicians than Christiaan Huygens.Ga naar eind5. It can be shown that Huygens himself considered his proofs for the first propositions in de ratiociniis as a paradigm of rigour which can be achieved in algebra.Ga naar eind6. In the light of such standards the complete failure of the proofs for the most important propositions of de ratiociniis in ludo aleae, which is presumably the most influential of all his mathematical papers,Ga naar eind7. is a sensation which cries for an explanation. It is astounding too that nobody within the some 340 years since the publication of this tract has noticed the mistakes contained in it, that generations of mathematicians and historians of mathematics who have scrutinized the tract since the time of Jakob Bernoulli, who wrote extensive commentariesGa naar eind8. on it, have not uttered the slightest objection against it. The tract De ratiociniis in ludo aleae came out as an appendix to Frans van Schooten's Exercitationum Mathematicarum Libri Quinque published in 1657 in Leiden. It is preceded by a letter of van Schooten to the reader and a letter from Christiaan Huygens to Frans van Schooten from April 27, 1657. Both letters serve as a kind of preface. They cover pages 517 to 520 of the book. The tract itself comprises 14 pages. Huygens had prepared it in Dutch. Van Schooten had translated it into Latin, not without some disputes between the two men, as is well known.Ga naar eind9. Evidence for the influence of Huygens' tract De Ratiociniis, which can be considered as one of the most effective pieces ever written in the history of mathematics if one relates its small size to its impact, is the fact that everybody who dealt with games of chance and with the slowly emerging calculus of probabilities in the 17th and 18th centuries referred to Huygens tract, commented on it or tried to solve Huygens' additional five problems and their generalizations.Ga naar eind10.
Huygens bases his ‘theory’ on a fundamental principle, the principle of a just game. Before we engage in understanding justice in a game of chance, we must remember the main motive for engaging in a game of chance. A game of chance changes the distribution of fortunes amongst the participants. You engage in a game of chance because you hope for a gain and you know that you have to pay for this hope with the risk of a loss. A presupposition for the justness of a game of chance is that the sum of the stakes is equal to the sum of the pay-offs of the players, or, in other words, that there is | |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 173]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
no third party like a banker or the owner of a lottery who takes a share of the stakes for his service to organize the game. In the simplest case of such a game we have two players who stake the same amount in order to engage in the game. Afterwards they play the game, the outcome of which is considered to be decided by chance. Whatever game of chance is played, its end, that is to say, who won the game and who is entitled to the loser's stake, which he can add to his own, is clear by unambiguous rules. These rules were known centuries before Huygens.Ga naar eind11. Huygens generalized the situation by admitting that the winner is entitled to only a part of the loser's stake. This part can be less than the whole stake, but, of course, it must be positive. Otherwise the idea of winning a game would be inverted. Huygens gave no reasons for such a generalization. But we can assume that the most prominent problem in gambling motivated such a generalization. The problem of pointsGa naar eind12. presupposes that a game is not decided by just one attempt of e.g. throwing a die, but by a whole series of single attempts. In general the parties involved agree that the winner of the whole game, and by that of all the stakes, is the party which first won a certain number of single games. If the whole game cannot be finished for some reason and the parties have to leave before any of them has reached the necessary number of wins, the stakes have to be divided according to the number of wins the respective parties are lacking. Since the whole game can be interrupted at any time, those concerned with the solution of the problem of points began at least in the 14th century to investigate the new distribution of the stakes after each single game. So it became interesting to know how much of the opponent's stake would go to the side of the winner of a single game, be it the first, the second, and so on up to the last. In general the winner of a single game would receive only a part of his opponent's stake. Using this motivation for Huygens' decision to allow even for the loser of a game a positive amount avoids resorting to a terminology of consolation prizes, which have no explanatory power at all.Ga naar eind13. After these remarks we can begin with Huygens' fundamental principleGa naar eind14., that in gambling the expectation or share that somebody can claim for something is to be estimated as much as that with which, having it, he can arrive at the same expectation or share in a fair game. Huygens' fundamental principle contains the term expectation, which is not explained explicitly. Accordingly, the expectation of a player A engaged in a game of chance in a certain situation is his share of the stakes if the game is not played or not continued. If the game is not played or continued with player A, who will be replaced by a player B, B has to pay A an amount equal to the expectation of A in this situation in order to engage in a just game. Huygens showed how to determine expectation in a simple case by the following example, which at the same time illustrated his principle of a just game: in order to engage in a choice between two closed hands one of which contains three and the other seven coins, it is just according to Huygens to pay five coins. Why is that just? In order to fill the two hands, we need another person ready to give five coins. With these two persons we have the simple original arrangement of the redistribu- | |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 174]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
tion of two equal fortunes, here twice the amount of five coins, into the amounts of seven and three coins. So this is a just game of chance which transforms a distribution of two equal assets into two unequal assets where the sums of the two distributions are equal. The difference between the winner and the loser in a just game, which for 7 and 3 is 4, could be 2, 6, 8 or 10 depending on the winner's share ranging from 6 to 10. Nobody in the middle of the 17th century or earlier asked questions concerning chance by which such a redistribution is achieved. Chance was a self-evident term. It meant uncertain, because unpredictable outcome. Which of two hands holding different amounts of coins contains more coins seemed at least as late as the 16th century to be as unpredictable as the outcome of a game of chess or the result of a competition in crossbow shooting.Ga naar eind15. Nobody before the middle of the 17th century thought about the effect of different skills. The simplest way to avoid this problem was to assume tacitly equal skills of the players involved. But today, when every effort is given to the evaluation of different degrees of abilities in sports or in chess, the case of equal skills seems to be all but self-evident. For Huygens and his two French predecessors, with their intention to subjugate chance to a mathematical calculus, it was essential for theoretical reasons to presuppose equipossibility as something elementary and clear. The reason for this is their conviction that the more complex cases, above all of the problem of points, can be reduced to cases for which throwing a die, tossing a coin, participation in a lottery or choosing between two hands are paradigms for unproblematic equiprobability. Huygens' very first example in the short introduction of his tract illustrates this.Ga naar eind16. If somebody contends to get a six with the first throw of a die, it is uncertain if he wins; but by how much he is closer to a loss than to a win is defined by the thing itself [my emphasis] and is determined by calculation. Huygens and his predecessors lacked a problem which forced them to distinguish between the self-evident equipossible and the contrary of it. Equipossibility seemed to be self-evident at least as long as there were only two possibilities, win or loss, heads or tails. Whenever dice or cards came into consideration, there were more than two alternatives. So mathematicians like Huygens felt obliged to transfer selfevident equipossibility in the case of two alternatives to the case of more alternatives. In this new case of more than two alternatives they referred explicitly to equipossibility. But a generation later, with Jakob Bernoulli, new cases of unpredictability, like dying at a certain age, were taken into considerationGa naar eind17. - cases that seemed to be neither equipossible nor reducible to equipossibility. For the successors of Huygens it began to matter that a more skilled and able player would win more frequently than his opponent in a series of games, they, above all Jakob Bernoulli, began to feel that frequencies were correlated to skills and abilities. Because equipossiblity had not become problematic to him, frequency did not figure in Huygens' tract of 1657.
The first three propositions of the tract contain the theoretical part necessary for the solution of the other eleven. | |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 175]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Huygens' first proposition just supplements his fundamental principle of a just game with a second person or a second player in order to return to the elementary situation of a new distribution of two fortunes which are equal into two different fortunes which add up to the same amount. If it is equally easy to obtain the amount a or b, the value of my expectation is to be declared as It goes without saying that there is no need to presuppose any notion of probability as available at the time in order to explain Huygens' understanding of expectation or his way of determining it.Ga naar eind18. In my opinion Bernoulli, who modified step by step Huygens' main concept of expectation, or of the value of a game, and who introduced a measure of probability into Huygens' calculus of expectations,Ga naar eind19. inspired all the attempts to give Huygens' concept of expectation a probabilistic interpretation. So Bernoulli had generalized Huygens' concept of expectation in such a way that it could be identified either with degree of certainty and eventually with probability or with the product of a certain amount and a factor later identified as the classical measure of the probability of obtaining it. As mentioned above, Huygens had some notion of probability, as is well attested by his later writings dealing with ‘verisimilis’ and ‘vraisemblance’,Ga naar eind20. but he did not connect his understanding of the probable with his notion of expectation. This will be confirmed by the two following propositions, which together with the first proposition offer the complete framework for a calculation of expectations à la Huygens and his predecessors. The second proposition saysGa naar eind21.: If it is equally easy to obtain the amounts a or b or c, the value of my expectation is to be estimated as The proof of the proposition introduces a third player. Any of the three players should have equal possibilities to win a or b or c, since all of them have to stake the same amount. Huygens tries to construct such a situation by the following system of mutual contracts which the first player completes with either of the other two playersGa naar eind22.: Given such a game, that I play with two others under the following condition: all three of us stake x and I complete this contract with one of them, if he wins the game, he shall give me b, and I shall give him b if I manage to win. With the other I agree to play under the condition that if he wins the game he shall give me c, or that I will give him c if I win it. It is clear that this is a just game. Under these conditions I have an equal chance to get b if the first wins, or c if the second wins, or 3x - b - c if I win; in this case I receive 3x, that is all the stakes, from which I concede b to one and c to the other. So if 3x - b - c equals a I have equal chances to obtain a or b or c.It is clear that Huygens used this construction for an evaluation of the expectation x of the player who has equal chances to obtain a or b or c, which is accordingly x = 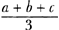 . The value of Huygens' expectation is in this case the same as that of expectation as defined by Jakob Bernoulli a generation after him. As long as the two notions of expectation are consistent, the equalitity of the two values for the different expectations can be taken as a confirmation of the soundness of Huygens' result. However, even if a result seems to be correct according to certain standards, the way it was obtained might still be wrong. . The value of Huygens' expectation is in this case the same as that of expectation as defined by Jakob Bernoulli a generation after him. As long as the two notions of expectation are consistent, the equalitity of the two values for the different expectations can be taken as a confirmation of the soundness of Huygens' result. However, even if a result seems to be correct according to certain standards, the way it was obtained might still be wrong.
| |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 176]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
If we want to exclude possible objections, we have to check if Huygens' construction agrees with the standards of a just game of chance. First we have to find out if the contracts are consistent with the idea of a game of chance. This implies that we have a new distribution of the fortunes or stakes of the three players after the game, which is impossible if the three amounts a, b, and c are all equal. Therefore we must assume that at least one of the three amounts, let us say a, is different from the other two. Since the first player receives the amount a in case of his winning, we can assume a > b and a > c, because otherwise the winner would gain less than at least one of the two losers. In addition we can assume that b > c, or b > c without any loss of generality, because the case b = c is covered by the following proposition 3. Huygens tries to transform, as we have seen, the equipossibility of the three cases that the first player or one of his two opponents win the game into the equality of the chances of the first player to obtain either a or b or c by the system of mutually symmetrical contracts between the first player and his two opponents. Since all three players stake the same amount x we are free, to choose any one of the three players as the first player who makes contracts with the other two. Accordingly, Huygens' construction has to secure equal chances to obtain a or b or c, not just for one but for all three players P1, P2, and P3. If this is so we shall find out by the following pay-off table which presupposes that the sum of the stakes is always a + b + c.
It clearly shows that P1 according to Huygens' construction has three equal chances to obtain a or b or c, but P2 gets a in case of his win and twice b in case of his loss, that is to say in case of the win by P1 or P3. Similarly P3 has one chance for a and two for c. Since we can assume without loss of generality that a > b > c the expectations of the three players, which of course should be as equal as their stakes, are different. In addition it is impossible to make all the contracts mutually symmetrical, because if P2 would receive c in case of a win by P3 that is to say the same amount he gives to P3 in case of his win the sum of the stakes distributed amongst the three players would be a + 2c. So we face a completely asymmetrical situation despite Huygens' intention of a perfect symmetry. In order to avoid such a seemingly paradoxical situation we have a choice between two possibilities: Either we give up Huygens' mutually symmetrical contracts or the principle that winning a game means obtaining more than the others. If we discard the system of mutually symmetrical subcontracts, the situation is remedied completely, but it clearly contradicts Huygens:
| |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 177]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
The second possibility is in accordance with Huygens but contradicts the very idea of a game of chance according to which a winner gains more or at least not less than a loser:
As a result of this analysis we can state that Huygens' proposition 2 holds only if we give up his mutually symmetrical subcontracts or the very meaning of winning a game. We face a similarly unpleasant situation if we look at the proof of Huygens' central proposition 3 which maintainsGa naar eind23.: If the number of cases I have for gaining a is p, and if the number of cases I have for gaining b is q, then assuming that all cases can happen equally easily, my expectation is worth The proof of this central theorem in Huygens' tract runs as follows. There are p + q players. Every one has p cases to win a and q cases to win b. Every player stakes the same amount x, so that the total stakes amount to (p + q).x. We take one player who agrees with p - 1 players that he will give them the amount a in case of his win and that he will receive the amount a in case that one of them shall win the game. With the other q players he contracts to pay each of them the amount b in case of his win and the right to the same amount in case that one of these q players shall win the game. Since each of the p + q players has the same chance to win the game, the first player has p - 1 cases which provide him with the amount a and q cases which give him the amount b and one case where he wins the game and receives the total stakes of (p + q).x of which he has to refund p - 1 players an amount a and q players an amount b. In order to give him p cases to obtain a, what remains has to be equal to a. This leads to the equation Since all the p + q players have to stake the same amount x, in a just game they must have the same expectation. This means that they have p chances for a win of a and q chances for a win of b. Huygens' construction of a system of mutually symmetrical subcontracts must apply not only to one player but to all of them. Therefore we have not only the p + q - 1 contracts mentioned by Huygens, but in total 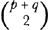 contracts which should be perfectly symmetrical: every player agrees with each of the other p + q - 1 players that he give him the same amount in case he wins as he receives from the other if the other wins. We can assume that the amounts a and b are different, e.g. a > b. Otherwise the stakes and all possible payoffs would be equal, contrary to the very idea of the game. And we can assume that p and q are different, because if they are equal proposition 3 could be reducedGa naar eind24. to proposition 1. contracts which should be perfectly symmetrical: every player agrees with each of the other p + q - 1 players that he give him the same amount in case he wins as he receives from the other if the other wins. We can assume that the amounts a and b are different, e.g. a > b. Otherwise the stakes and all possible payoffs would be equal, contrary to the very idea of the game. And we can assume that p and q are different, because if they are equal proposition 3 could be reducedGa naar eind24. to proposition 1.
| |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 178]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
It can be shown that proposition 3 and this system of perfectly symmetrical subcontracts are incompatible, except that the idea of the game is sacrificed, that is to say that the winner gets less than some of the losers. For the failure of the proof under Huygens' presuppositions it suffices to offer one counterexample like the simple case of p = 2 and q = 1. In this case we have a system of mutually symmetrical contracts between the three pairs of players (P1, P2), (P1, P3), and (P2, P3). The contract between P1 and P2 ensures that P1 gives the amount a to P2 if he wins and that P2 is giving him the same amount a if P2 wins. The same holds for P3 who receives the amount b from P1 if P1 wins and who pays the same amount b to P1 if P3 wins. If P2 wins the game, he will take a because a > b; he shall pay the amount a to P1 and the amount b to P3 according to his contract. In the same way P3 as the winner of the game takes the amount a for himself and pays the amount b to both P1 and P2. But then the total pay-off of 2b + a is less than 2a + b, the sum of the stakes. So it is clear that it is impossible to have a complete system of mutually symmetrical contracts and at the same time to ensure the amount a for the winner, whoever he is, as is shown in the following pay-off table:
In addition to what has been explained above the pay-off table shows that, contrary to equal expectations for all three players, P1 has two chances for a and one for b, whereas P3 has two chances for b and one for a; finally P2 has either three chances for a or two chances for a and one for b, as is the case for P1, depending either on Huygens' assumption that the sum of the stakes is 2a + b or on our respect for the symmetry of the subcontract between P2 and P3. In the first case P2 would have to pay the amount a in order to engage in a game in which he can neither win nor lose, which contradicts the motive to engage in gambling. However, in this case the sum of the stakes of the three players would still be 2a + b, since , but in contradiction to Huygens' presupposition that all players stake the same amount. In the second case, which gives priority to the symmetry of the subcontracts, here between P2 and P3, the expectation of P2 is equal to that of P1 but different | |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 179]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
from that of P3. This means that P3 would have to stake 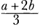 , again in contradiction to Huygens' presupposition. , again in contradiction to Huygens' presupposition.
In order to escape this chaos of contradictions, we have to give up either the principle of mutually symmetrical subcontracts or the principle that the winner gets at least as much as a loser. If we accept the amount b which is less than a for P2 in case of his winning, we obtain the following pay-off table:
If the fact that the winner P2 gets less than the two losers, in contradiction to common sense but in formal accordance with Huygens' text, seems unacceptable, we still can discard the mutual and perfectly symmetrical contracts between each pair of players. So we assume that the winner of a game is always entitled to the amount a, because a > b, and that every player has two chances for a and one for b (Al). As a consequence of A1 the sum of the stakes will be 2a + b (C1). The pay-off table for the case p = 2 and q = 1 is uniquely determined if we begin with the assumption that P2 gets the amount a and P3 the amount b if P1 wins.
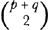 subcontracts which secures for every winner of a game the amount a and each of the p + q players p chances for a win of a and q chances for a win of b. But these subcontracts are not mutually symmetrical. subcontracts which secures for every winner of a game the amount a and each of the p + q players p chances for a win of a and q chances for a win of b. But these subcontracts are not mutually symmetrical.
| |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 180]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
The system can be described in the following way. If the p + q players are numbered from 1 to p + q, the pay-off for the players if player Pj wins the game is that Pj and all the players from Pj + 1 with 1 ≤ i ≤ p - 1 and j + i counted modulo p + q receive the amount a whereas all the other players get b. This system is not mutually symmetrical; for if Pj + 1 wins the game, Pj receives the amount b and not a, as he would in case of a mutually symmetrical contract between Pj and Pp + 1. This new contract system secures for every player the amount a if he wins; in addition he gets (p - 1)-times the amount a and q-times the amount b in the p + q - 1 cases in which one of the others wins the game. Instead of Huygens' pairwise symmetry we have a symmetry in sum or in the average: as often as he pays the amount a he will receive the same amount but not necessarily from the same persons. Huygens either had not seen that or ignored it. To assume that he understood the problem and did not care would make a young man of 27 too cynical for his age. In addition Huygens' theory of games of chance would be valid only if we allow him to pervert the very sense of gambling. At least in the numerical example with three cases for 13 and two for 8, which Huygens chose in order to illustrate proposition 3, the first player as the winner of the game receives the higher amount 13. The assumption that Huygens understood the situation and despite that did not care seems therefore much less convincing than that he had just not seen the consequences of his system of mutually symmetrical subcontracts.
As we have seen, Huygens' system of subcontracts fails completely to provide the conditions necessary for the validity of his propositions 2 and 3. To infer from this very system, the implications of which Huygens obviously had not understood, a juridical background of his concept of expectation seems to be at least questionable. A possible answer to the question why Huygens was so eager to use this system of mutually symmetrical contracts which follow the old legal maxim of the ‘do ut des’, is that he felt obliged to superimpose this construction on the very old practice of distributing assets in order to make it at least look legal or ‘just’. Such a concession may be connected with the fact that quite a few of Huygens' successors in the mathematical treatment of games of chance, including the translator of his tract into EnglishGa naar eind25. published in 1692, preferred to publish anonymously, because they were afraid that their names could be connected with the frivolous atmosphere of a gambling den. Huygens himself was very much aware that some would accuse him of supporting with his tract the frivolity of gamingGa naar eind26., but he hoped that most of his readers would appreciate the utility of his work. The first three propositions of Huygens' tract describe, as we have seen, a practice of distributing fortunes for which the criterium of adequacy was established without reverting to any concept of probability. The third proposition can be interpreted as a special case of the generalized second proposition. The generalized proposition 2 maintains that the expectation, in case of i equal cases of winning any of the i amounts aj, j = 1,...,i, is | |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 181]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
If we assume that the the first p amounts aj are equal to a1 and the remaining i - p are equal to ap + 1, we have the premises of proposition 3. It allows us now to treat an asymmetrical situation in the new distribution of two fortunes. In order to understand this, we introduce two new players who can win either a or b but with unequal chances which are as p to q. Huygens procedes from problems concerning equal cases to those involving unequal casesGa naar eind27. in the same way as he developed the laws of impact in De motu corporum ex percussione, which begins with the impact of two bodies which have equal mass and collide with the same velocity and ends with the impact of bodies with unequal mass colliding with different velocities. This can be illustrated by Huygens' solution of the problem of points. In the simplest case it assumes two parties which have staked the same amount a/2 and agree that the party which first won a certain number of games, say 5, is entitled to take the whole stake a. Huygens did not take much trouble to emphasize that the parties have equal chances of winning a single game. Such a restraint may justify the idea that he saw no problem in assuming something like equal possibility for win and loss in a single game. At least the calculation of the different expectations treats win and loss as two cases with the same weight. If we symbolize by E(m, n) the expectation of the first party to win the whole game when it still lacks m wins of single games and the other party n wins, Huygens' first proposition can be applied: in the next game there is one case, namely that the first party wins it and so reduces the number of lacking wins m by one, and one case in which the second party wins it and so reduces the number of lacking wins m by one. So we have: The formula describes Huygens' successive construction of E(m, n) which for increasing values of m and n shows in reverse order the distribution-process as a dynamical development. Beginning with E(0,k) = a for k ≥ 1, E(l,0) for l ≥ 1, and E(r, r) = a/2 for all r ≥ 1, Huygens is able to calculate successively all values of E(m, n). In proposition 4 he determines E(1,2) according to the rule: In the following three propositions he successively calculates, in the same way, E(1,3), E(2,3), and E(2,4). The same principle which was applied by Huygens (and Pascal) to the solution of the problem of points was used already in a manuscript of 1400 to calculate E(1,2) correctly.Ga naar eind28. The problem of points was treated in a different way, but not solved, in printed Italian arithmetics like Luca Pacioli's Summa de Arithmetica of 1494, Cardano's Practica Arithmetice of 1539 or Tartaglia's General trattato of 1556.Ga naar eind29. Knowledge of the different attempts to solve the problem of points spread slowly outside Italy. Careful research on this problem in textbooks of arithmetic of the second half of the 16th century and in the first half of the 17th century has not yet been carried out. We know at least that people in Paris were familiar with the mathematical | |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 182]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
‘folklore’ of the problem of points. An example for this is given by the notorious Chevalier de Méré, who had confronted Pascal with this and another problem and of whose opinions concerning these problems we posess an account, maybe distorted, by Pascal.Ga naar eind30. At any rate it is not very probable that Huygens had no information about this tradition and it is clear that he was familiar with the idea of gambling which formed the approach described above. In the light of this tradition an obvious question, which, however, is far beyond the scope of this article, is: what justifies the claim of Pascal and Huygens to be the first to approach problems of chance mathematically? That Huygens was in touch with different areas of the low sciences, where the problem of points had been dealt with centuries before, is well known. Another hint for such a connection is provided by the form of Huygens' De Ratiociniis, which resembles the style of publication developed amongst the reckoningmasters and mathematical practitioners in Germany in the beginning of the 17th century.Ga naar eind31. The case of Peter Roth will suffice to demonstrate this. Peter Roth had published in his Arithmetica Philosophica of 1608, in the first part, the solutions of the cubic equation according to Cardano's account in the Ars Magna. published in 1545. In the second part he had solved the hundred cubic problems published by his colleague and competitor Johann FaulhaberGa naar eind32. using up to 28 different methods for the same problem. In the third part he had published some 70 problems leading to equations of degree 4 to 7 without any hint to their solution. With the second part of the Arithmetica Philosophica Roth had made Faulhaber's knowledge about the application of Cardano's rules to the solution of cubic problems public knowledge which freed interested amateurs from the necessity to go to a reckoningmaster like Faulhaber for instruction. But by his third part consisting of problems which led to equations of a degree higher than three he had announced problems without any hint how to obtain their solutions. For instruction in this new domain of problems interested clients would have to consult Roth and pay for it. Huygens' De ratiociniis shows the same formal presentation. A theoretical part consisting of the first three propositions, the complete solution with explanation of the following 11 problems, and in a final part five most demanding problems without any hint to their solution except that he gave the result for three of them in order to indicate that he himself was able to solve these problems. Of course, in contrast to reckoningmasters like Roth or Faulhaber, Huygens was not interested in making money by the instruction of interested clients, but he was interested in non-material rewards like prestige and reputation as the Archimedes of his age.Ga naar eind33. Any hint of a tradition of calculating games of chance before his time would detract from his reputation as a mathematician and make it more difficult for him to clarify his own contribution. Huygens' letter to van Schooten from April 27, 1657, which was published as a preface to his tract, can be read in the same line. Huygens had maintained in it that he did not know if Pascal and Fermat had used the same method as he because the two French mathematicians had kept their approach a secret. So Huygens had to develop his calculus from the very beginning. This is a very distorted account of the real story. In fact, Huygens was informed to some extent about the methods and results of Pascal and Fermat through his correspondence with Carcavy and Mylon, who served as mediators. So Carcavy had confirmed in his letterGa naar eind34. from September 28, 1656 that Pascal used the same princi- | |||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 183]
| |||||||||||||||||||||||||||||||||||||||||||||||||||
ple as Huygens which is a generalized form of Huygens' proposition 3. We may therefore conclude with all caution that Huygens knew more than he was willing to concede about an older tradition of treating games of chance according to which he modelled his approach as reconstructed above. |
|


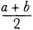 .
.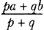 .
.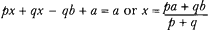 .
.