Logo DBNL
De Zeventiende Eeuw. Jaargang 12 (1996)

De Zeventiende Eeuw. Jaargang 12

(1996)– [tijdschrift] Zeventiende Eeuw, De–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

Huygens's Dioptrica
Fokko Jan Dijksterhuis

In 1979, at the end of the symposium on Huygens's life, Rupert Hall remarked that it was not easy to understand how all the multifarious activities of this man's life fit together.1. The diversity of problems he investigated and the diversity of his approaches has made it difficult to develop a coherent interpretation of Huygens's activities. He was a transitional figure in the development of mathematical physics from Galileo and Descartes to Newton and Leibniz. A pure problem-solver he was called at the symposium; someone who opportunistically approached problems which had drawn his attention from external stimuli. It has been 16 years since and much work on getting a balanced sense of Huygens's activities has been done. Joella Yoder in particular has contributed to our understanding of Huygens with her detailed study of his mechanics.2. She has shown that mathematization of nature was central to Huygens's science. The present paper intends to show how a study of his dioptrics - the mathematical study of refraction - can further add to a coherent picture of the science of Christiaan Huygens.

Although dioptrics was one of Huygens's main interests throughout his life, his contributions to the field are little studied by historians. Huygens's dioptrics was one of the most advanced mathematical theories of lenses and telescopes of the 17th century, but he did not publish it during his lifetime. What interests me, is his focus on practice in his mathematical investigations. Huygens tried to improve the telescope by means of theoretical study. In this regard he continued the work of Johannes Kepler (1571-1630) and René Descartes (1596-1650). In the first part of this paper, I will give a sketch of the development of 17th-century dioptrics which, in my opinion, was focused on practical questions relating to the telescope. Dioptrics not only had got an impulse from the work of craftsmen, but also kept being aimed at yielding practical output, although not very successfully. Secondly, I will give an outline of Huygens's contributions to dioptrics. He directed his rigorous mathematical analysis to practical problems relating to the telescope. He also developed profound practical skills in producing and using telescopes, but in the end he did not succeed in realizing his theoretical designs for perfect telescopes. Finally, I will explicate my views on the consequences of this interpretation for our understanding of Huygens's science.

The telescope and dioptrics, 1600-1650

The invention and subsequent improvement of the telescope in the first half of the 17th century was the sole business of practice. Galileo Galilei (1564-1642) introduced the instrument to science, but did not show a particular interest in its theoretical background. In contrast to mechanical problems, the telescope did not induce



illustratie
1. Spherical aberration of a bi-convex lens. O.C., vol. 1, p. 224.


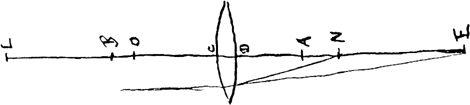
him to scientific reflection towards the workings of the instrument. He discovered, for example, the advantages of adding a diaphragm to telescope lenses, but he did not try to explain its working theoretically.3. Johannes Kepler was the first scholar who thought an optical analysis of the instrument was prerequisite to its use in astronomy. This resulted in the detailed mathematical analysis of the refractional properties of lenses in Dioptrice of 1611.4. It took some time before his work was continued. The astronomers and specialized craftsmen who developed the telescope in the first half of the seventeenth century confined themselves, like Galileo, to practice.

Using the results of his earlier Paralipomena5., in Dioptrice Kepler reinforced the mathematical grip on refraction by analyzing the focal properties of lenses. He used an approximate rule for refraction, which only applied to a limited range of angles of refraction. This rule said that for angles of incidence smaller than thirty degrees the angle of deviation is nearly one third of the angle of incidence.6. With this rule, Kepler roughly determined the focal distance of the basic types of lenses. On the basis of this he explained how configurations of convex and concave lenses produce magnified images of objects seen through them. Kepler also explained how two convex lenses could yield a telescopic effect, which had not been suggested before.7. A telescope consisting of two convex lenses was first built and used by Christoph Scheiner (1573-1650), who discovered its advantages over the initial configuration of a convex and a concave lens.8. Although Kepler did not offer a fully exact dioptrical theory, his was the first mathematical explanation of image formation by telescopes.

Kepler's efforts towards a scientific understanding of lenses were first continued 25 years later by René Descartes.9. La Dioptrique10. offered what Kepler had lacked: an exact law of refraction. With the sine law Descartes was able to show that distortions of images produced by lenses were inherent to the spherical shape of their surfaces. When rays AB, DE (Ill. 1) are refracted by a lens, they will not intersect the axis NOK in one point K but in different points C, F. This phenomenon is called spherical aberration and produces slightly fuzzy images. Descartes proposed alternative shapes, based on conic sections, with which lenses with perfect focal properties might be made. Writing for craftsmen, Descartes also explained how such conical lenses could be ground. Nevertheless, subsequent efforts to actually produce these lenses failed. Descartes' theoretical solution to the problem of imperfect focal properties of telescope lenses, turned out to be impractical. As a matter of fact, the only contribution to the 17th-century development of the telescope from the side of theory, was Kepler's telescope consisting of two convex lenses.

Although far from complete, this sketch of dioptrics in the first half of the 17th century is suitable to show its focus on the telescope. The impulse for Kepler's renewed investigation of dioptrics and its subsequent reinforcement of mathematical analysis had come from the crafts. Additionally, the efforts of Kepler, Descartes and others not mentioned, were aimed at having theory contribute to the practical improvement of the telescope. This pattern recurred in Huygens's dioptrical investigations. His interest in dioptrics arose because he thought he could contribute to the improvement of the telescope. When he subsequently set himself to an extensive treatment of the theory of dioptrics his focus kept being on practice. The rigorously mathematical treatise he produced after a year contained a detailed analysis of the lenses actually used in telescopes. Fifteen years later this was followed by a detailed analysis of spherical aberration, aimed at designing a telescope in which it was neutralized.

Huygens's treatise on dioptrics of 1653

Huygens's interest in dioptrics started at the end of 1652 with a theoretical discovery he made as a result of his study of Descartes's mathematics.11. Descartes had not provided the readers of La Dioptrique with mathematical proofs of his ideas. His mathematical deduction of perfectly focusing surfaces could be found in La Geometrie, where he derived, using the sine law, four classes of ovals which could be used to produce perfect lenses.12. Generally speaking, such ovals are closed curves which may reduce to ellipses and other conical sections in special cases. Huygens's discovery consisted of the discovery that one of Descartes's ovals reduces to a circle in particular circumstances.13. As the shapes of the lenses used in telescopes were based on circles, Huygens expected his discovery to be of practical value. His letters from this period show that it was this expectation which made him pursue his dioptrical investigations. Huygens started inquiring after the particulars of the art of lens grinding and apparently had a craftsman grind him some lenses.14. The practical value of his initial discovery turned out not to be as great as Huygens had expected and he did not return to it after its initial conception.

Yet, Huygens's interest in telescopes had been aroused and he zealously started dioptrical studies. In 1653, Kepler's treatment of spherical lenses was the most advanced which had been published. Various letters of Huygens show that he soon had a grasp of the basics of dioptrics and rapidly advanced beyond Kepler's theory.15. By means of the sine law, Huygens could make exact derivations, whereas Kepler had only been able to give approximations. Moreover, Huygens took the thickness of lenses into account and based his derivations on a mathematical conceptualization of spherical aberration. In this way he established exact rules for the focal distance for any type of lens. At the end of 1653 a first draft of a treatise on dioptrics was ready, containing a systematic, exact and general theory of the properties of spherical lenses. In order to illustrate the way Huygens attacked dioptrical problems, an outline of his theory is given.

In order to account for the spherical aberration of a surface in a mathematical way, Huygens used the concept of ‘punctum concursus’.16. When, for example (Ill.

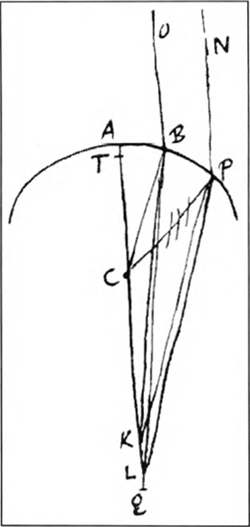
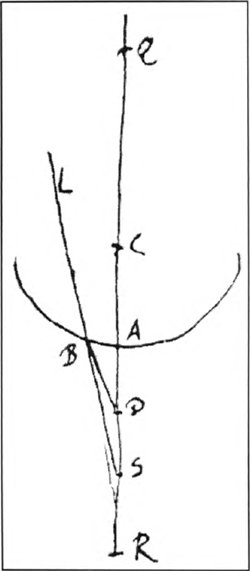
2), parallel rays OB, NP are refracted by a spherical surface ABP, they will not intersect the axis ACQ in one point Q but in different points L, K. Yet, beyond Q no refracted rays will intersect the axis and when a ray OB is nearer to the axis intersection L will increasingly be closer to Q. Huygens called this limit point Q the ‘punctum concursus’ of the refracted rays, which is approximately the focus of the refracted rays. Determination of focal distances now consists of finding expressions for ‘punctum concursus’ Q the characteristics of the incident rays and the refracting surface.

In the case of a bi-convex lens the determination of its focal distance consists of the following steps (Ill. 1). When parallel rays AB, DE are incident on a bi-convex lens OHB, they are refracted twice. To determine the focal distance OK of the lens, the distance to the place where the refracted rays BC, EF intersect the axis NO, the refractions at both surfaces H and O need to be treated separately. The refraction at the anterior surface H involves the refraction of parallel rays at a convex surface. In the eighth proposition of his treatise, Huygens determined the ‘punctum concursus’ Q (Ill. 2) for parallel rays NP, OB refracted by a convex spherical surface ABP.17. Q is found by the relation AC:CQ = n, where AC is the radius of ABP and n is the index of refraction. He then proved that no refracted ray BL, PK intersects the axis NO beyond point Q and, finally, that Q is the limit point of the intersections K, L when the incident rays NP, OB draw nearer to the axis NO. When ABPC is a glass body surrounded by air, the focal distance AQ will be exactly three times the radius AC of the surface. For this particular case, Kepler had found the same result, yet without the exactness Huygens established.

After refraction at the anterior surface the rays are not parallel anymore: they converge towards the focus of this surface. Huygens determined the focal distance of converging rays refracted by a concave surface in the twelfth proposition of his treatise (Ill. 3).18. He derived an expression for the position of ‘punctum concursus’ D, to which the rays LB converge after refraction, by means of three given points S, C and Q.S is the point towards which the rays converge before refraction; C is the center of the refracting surface. Q is the ‘punctum concursus’ for parallel rays coming from the direction of R and can be found by means of the sine law. Huygens stated that D is found by means of the proportionality SQ:SA = SC:SD.

In the sixteenth proposition, Huygens combined the preceding results (Ill. 4).19. On the axis EL, the centers A and B of surfaces C and D are drawn. First, ‘puncta concursa’ E and L for parallel rays of each surface are constructed by means of the eighth proposition: CA:EA = DL:LB = n. Then N, the focus of the lens, is constructed by means of the twelfth proposition: EL:ED = EB:EN. Parallel rays tend to E after refraction at the anterior surface C and they are refracted towards N by the posterior surface D. This was an exact and rigorous determination of the focal distance, or more precisely the ‘puncta concursa’, of a bi-convex lens. In his concluding remarks, Huygens showed that in the case of a glass lens and when the thickness is ignored, the focal distance can be derived from the radii of both surfaces directly. Kepler, ignoring the thickness of the lens and treating only glass lenses, could give a determinate rule only for lenses with equal surfaces.20. In this case, as Huygens showed, the focal distance equals the radius of the surfaces. Although Huygens had arrived at a similar result in this case, his was based on a general and exact determination of focal distances.



illustratie
2. Focal distance of a single convex surface. O.C., vol. 13 (1), p. 33.


Huygens was the first to invoke the sine law to determine the focal properties of lenses. Yet, abstaining from publication, he lost priority to Isaac Barrow (1630-1677), who published his theory of focal distances in Lectiones XVIII (1669).21. Comparing both theories, Huygens's orientation towards practical problems is clear. The properties of lenses were not Barrow's primary concern: he only gave them as an helpful application of his theory. The core of Barrow's theory consisted of a detailed analysis of image formation in spherical surfaces, which included mathematically sophisticated problems like refraction of obliquely incident rays. Huygens, on the other hand, confined himself to problems relating to lenses in tele-

scopes. He treated complex problems like refraction of converging rays, but only because, and in so far as, they were relevant to the working of telescopes. In the second part of his treatise he extended his theory to the magnification of objects seen through a system of lenses. This subject, of direct relevance to the use of telescopes, was not treated by Barrow. Huygens had also planned a discussion of telescopes, like Kepler had given in Dioptrice, but he did not elaborate it. It is likely that Huygens considered the application of his theory of lenses to the use and improvement of telescopes, but at that moment he first turned to the practice of telescope making. Although he did not explicitly apply his theory of lenses to the improvement of telescopes, it is clear that Huygens's focus in dioptrics was on the telescope.

Telescopes and dioptrics in Huygens

From 1654 onwards Huygens and his brother Constantijn acquired the art of grinding and polishing lenses, and built telescopes and microscopes. These activities eventually led to Huygens' discoveries regarding the planet Saturn. The period of telescope building and astronomical observing lasted until the early 1660s. By that time Huygens had invented a new type of ocular consisting of two lenses, nowadays called Huygens's eyepiece. The ocular is the part of a telescope turned towards the eye, which projects the image produced by the objective lens into the eye. Compound oculars had been made before by craftsmen, but Huygens had invented a particular configuration. Evidently he had tried to optimize it by theoretical analysis, but he had to admit that the optimal configuration could only be found by means of trial and error.22. His analysis provided no more than broad directives for the size and mutual distances of the lenses. We may conclude that this practical achievement did arise out of Huygens's theory only indirectly.

When, in the 1660s, Huygens turned to theoretical study again, his aim was using it to improve the telescope. He had the idea that the influence of spherical aberration on the quality of an image produced by a telescope could be reduced by configuring the lenses properly. The idea that this could be possible had occurred to him in the early 1650s. In his treatise of 1653, he remarked that the spherical aberration of a plano-convex lens is considerably less when its plane side is turned towards the object as compared to when the convex side is turned towards the object.23. Apparently the position of a refracting surface in relation to light rays influenced the amount of aberration, and the aberration of one lens might be decreased by another lens. In 1665 Huygens set out for a detailed investigation of spherical aberration in order to design a telescope better than any telescope made before, which can match those with conical lenses.24.

Huygens' analysis of spherical aberration is an example of his skill to apply mathematics to concrete objects. It involved finding a relationship between the curvature of a lens and the amount of aberration of a ray at a particular distance from the axis. I will not treat this analysis in detail. The problem was so complex, that Huygens arrived at a theoretical solution for only a few particular configurations of lenses. Its practical application, which had to wait a few years, unfortunately proved disappointing.25. Besides, in the meantime Huygens' analysis had led to



illustratie
3. Focal distance of converging rays. O.C., vol. 13 (1), p. 71.


another idea, which he announced with an ‘Eureka’ so typical of him.26. In 1669 he had discovered how to simulate the properties of a hyperbolical lens by means of a lens compounded of two spherical lenses. Unfortunately, Huygens's high hopes soon were to vanish. Before he could put his new invention to practice Isaac Newton (1642-1727) thwarted his plans. That year Newton published his theory of different refrangibility of colored light rays.27. The colored fringes which disturbed images by telescopes are an example of this. Until then, Huygens had not paid

serious attention to these fringes and now they turned out to diminish all advantages of his inventions. So, Huygens looked up his notes and decidedly crossed out the once victorious ‘Eureka’ together with a large part of his theorems.

Dioptrica: science and technology

In my opinion, Huygens's dioptrics was part of a tradition of practice-oriented optics in the first decades of the 17th century. In this tradition theory was applied to the practical problems of using and improving the telescope. Huygens built on the work of Kepler and Descartes and he might have had the clearest perception of the consequences of such an approach. Huygens did not publish his theory and neither did similarly practical-minded students of dioptrics. The few works on geometrical optics which went through press after Descartes's La Dioptrique were little practicalminded, like Barrow's Lectiones XVIII. It is questionable whether publication would have made much difference to the development of the telescope. If necessary, knowledge obtained by men like Huygens probably found its way to users and designers of telescopes through other channels. In the 1660s Huygens, for example, communicated his theory to the group around Jean Picard (1620-1682) by means of copies of his manuscript. The influence of this to their telescopic activities is, however, hard to determine.

Huygens' dioptrics as well as 17th-century dioptrics in general was relatively unsuccessful in contributing to the improvement of the telescope. Yet, it is important to realize that his dioptrics is an example of 17th-century efforts to realize utilitarian ideals. Huygens was not unique, his dioptrics is part of a broader development in early modern science in which science and technology came closer to each other. In England for example, a group around Christopher Wren (1632-1723) and later Robert Hooke (1635-1703) approached dioptrics in a way, which would be worth comparing with Huygens's. In this paper I want to draw attention to the possible significance of Huygens's practical-mindedness in his dioptrics for his science in general. Dioptrics was one of the first subjects he treated extensively and it would remain one of his main concerns throughout his life. His dioptrics was one of his early efforts to mathematize nature, and shows his ability to do so. In his dioptrics, his mathematizing of nature was also connected with a focus on practical problems. Huygens was not a ‘vernufteling’28. like Stevin had been, as his roots were in scholarly science, not in the crafts. But he might be called a scientistengineer: first of all a scientist, yet with a clear focus on technology.

Let me conclude with a tentative remark on how Huygens's practicalmindedness might shed more light on his scientific personality. Huygens is known as a problem-solver in questions relating to the mathematization of nature. A very skilled problem-solver, but lacking a unifying program for his various projects. It has been said that Huygens would never write a ‘Principia’. How could he have? Has anybody ever heard of a ‘Principia Telescopii’ or ‘Principia Horologii’? Engineers and artisans realize that nothing is ever perfect, that every accomplishment is part of an ever-lasting process of improvement. Looking at Huygens's mathematical analysis of the properties of lenses in the 1650s, 1660s and 1680s, a pattern of increasing exactitude is discernible. A mathematical analysis of this sort



illustratie
4. Focal distance of a bi-convex lens. O.C., vol. 13 (1), p. 87.


is never finished, because there always remain parameters to be accounted for. Does a consideration of this sort bring into coherence our picture of Huygens as a problem-solver? I think it is promising to view Huygens as a scientist-engineer. Yet, the above statements have still to be substantiated and, of course, an exceptional personality like Huygens can hardly be expected to be reduced to one characteristic ever.

Vorige Volgende

Over dit hoofdstuk/artikel

auteurs