Tabu. Jaargang 26

[p. 103]

Optimality Theory: achtergronden en toepassingen
Helen de Hoop

0 Inleiding

Optimality Theory (van nu af aan OT) is een theorie van taal en grammatica, die vooral via de fonologie in de taalkunde is doorgebroken door een manuscript uit 1993 van de fonoloog Alan Prince en de mathematisch natuurkundige Paul Smolensky (Prince en Smolensky 1995).^* In OT kan een grammatica opgevat worden als een verzameling gelijktijdige, ‘zachte’ welgevormdheidscondities. Dat condities gelijktijdig van toepassing zijn op (representaties van) zinnen, is een bekend uitgangspunt in de generatieve syntaxis, maar dat ze zacht zijn, oftewel conflictueus, opent nieuwe mogelijkheden voor de generatieve grammatica, wat bevestigd wordt door een groot aantal studies, niet alleen binnen de fonologie, maar recentelijk ook binnen de syntaxis. Daarmee is OT in elk geval een interessante taalkundige theorie die verdere aandacht verdient.

Wat misschien niet iedereen weet, is dat OT voortkomt uit het connectionisme, een computationele theorie die geïnspireerd is door de structuur van het menselijk brein. Ons brein bestaat uit miljoenen neuronen die met elkaar in verbinding staan in zogenaamde neurale netwerken. Klassieke cognitiewetenschappers ontkennen niet dat er een verband moet zijn tussen deze fysieke organisatie van het brein en cognitieve processen zoals perceptie, geheugenopslag, taalverwerking, etc., maar hebben ook geen theorie over die relatie. Kunstmatige neurale netwerken (connectionistische modellen) zijn weliswaar abstracte vereenvoudigingen van natuurlijke neurale netwerken, maar analyses van de relatie tussen cognitieve verwerking en kunstmatige neurale netwerken maken de stap naar natuurlijke neurale netwerken allicht kleiner.

In een connectionistisch model worden ingewikkelde processen uitgevoerd door eenvoudige communicatie tussen eenheden, units, die een soort van abstracte neuronen voorstellen. Connectionisme staat dus dichter bij neurowetenschappen dan symbolische theorieën. Computationele inzichten voortvloeiend uit de ontwikkeling van connectionistische PDP-modellen (zie §1) hebben op hun beurt theoretische neurowetenschappers geïnspireerd. Daarmee is duidelijk geworden dat deze modellen een bijdrage kunnen leveren aan de theorievorming over de relatie tussen neurale structuur en neurale verwerking. Dat maakt een wiskundig uit het connectionisme afgeleide theorie als OT extra interessant: het is een theorie die niet alleen een bijdrage kan leveren aan de taalkunde, maar ook een brug kan slaan tussen taalkunde als puur symbolische theorie en connectionistische, neurowetenschappelijke theorieën.

Smolensky, een PDP-er van het eerste uur, aan wiens brein ook de voorloper van OT, harmonieuze grammatica (zie §3), ontsproten is, benadrukt in Smolensky (1995) dat symbolische theorieën (zoals bijvoorbeeld de generatieve taalkunde) en connectionistische beschouwd moeten worden als benade-

* Ik bedank de studenten van het werkcollege ‘Optimality in Syntax’ (Groningen, tweede trimester '95/'96) wier vragen en opmerkingen hebben bijgedragen aan de totstandkoming van dit artikel, en Jack Hoeksema en Ron van Zonneveld voor commentaar op een eerdere versie.

[p. 104]

ringen van één en hetzelfde cognitieve systeem, doch op verschillende niveaus van beschrijving. Het beschrijvingsniveau van connectionisten ligt weliswaar dichter bij de neurale realiteit maar het is nog altijd abstracter dan deze. Smolensky presenteert expliciete principes voor zijn nieuwe cognitieve architectuur ICS (wat staat voor Integrated Connectionist/Symbolic architectuur) die duidelijk moeten maken dat connectionisme niet alleen in staat is hogere cognitieve processen te verklaren, maar ook dat connectionistische principes op hun beurt symbolische theorieën kunnen aanvullen en verrijken.

Smolensky hecht er veel waarde aan dat ICS niet een voorbeeld is van een puur implementationele strategie, waarbij inzichten uit symbolische theorieën domweg geïmplementeerd worden in connectionistische netwerken. In Smolensky's benadering leveren connectionistische principes op hun beurt een essentiële bijdrage aan symbolische theorieën. Hij laat dit zien met betrekking tot wat hij een van de sterkste gebieden van symbolische theorievorming noemt, de generatieve grammatica. Het feit dat condities zacht zijn, bijvoorbeeld, volgt automatisch uit connectionistische principes, en werpt een geheel nieuw licht op taalkundige problemen en theorievorming.

1 Parallelle gedistribueerde verwerking

Een belangrijk type connectionistische modellen wordt gevormd door de zogenaamde PDP-modellen (PDP staat voor Parallel Distributed Processing). PDP-modellen liggen aan de basis van OT, en daarom zal ik enkele van de karakteristieke eigenschappen van PDP-modellen hier kort bespreken (zie voor een uitgebreidere introductie Rumelhart, Hinton en McClelland 1986).

Het specificeren van een PDP-model begint altijd met het specificeren van een verzameling processing units en waar deze voor staan. In principe kunnen deze units gebruikt worden om allerlei uiteenlopende elementen te representeren (bijvoorbeeld eigenschappen, letters, woorden, concepten of abstracte elementen waarover betekenisvolle patronen kunnen worden gedefinieerd), maar het kenmerkende van gedistribueerde (distributed) connectionistische modellen is, dat de units te zamen patronen vormen waaraan een betekenis kan worden toegekend. De representatie van een propositie is dan bijvoorbeeld niet vastgelegd op één unit, maar als het ware verspreid over vele units, units die tegelijkertijd deel uitmaken van de representatie van andere proposities.

Een ander voorbeeld betreft de representatie van letters in een connectionistisch netwerk. Als elke letter van het alfabet gerepresenteerd zou worden door één specifieke unit, dan zouden we spreken van een lokaal representatieschema. Maar als de units slechts onderdelen van letters representeren, zodat de letter T bijvoorbeeld weergegeven wordt als de gezamenlijke activiteit van de units die staan voor ⊥ en ⎴, dan spreken we van een gedistribueerde representatie. Het aantrekkelijke van zo'n systeem is dat de letters E en F in hun representatie dichter bij elkaar liggen dan de E en de O, omdat de eerste twee letters meer kenmerken gemeen hebben.

[p. 105]

Alle verwerking wordt gedaan door de units. Hun taak bestaat eenvoudig uit het ontvangen van input van andere units, en het berekenen en doorsturen van een output. Aangezien units tegelijkertijd hun taak kunnen uitvoeren, is het systeem inherent parallel. Er zijn drie typen units in een model: input units, die input ontvangen van buiten, output units, die signalen naar buiten zenden, en verborgen units, die onzichtbaar zijn voor uitwendige systemen.

Behalve een verzameling processing units, hebben we ook een representatie nodig van de staat van activatie waarin een systeem verkeert op een zeker tijdstip t. In PDP-modellen wordt het activatiepatroon van een verzameling processing units op een tijdstip t weergegeven als een vector a(t). Een vector is niets anders dan een serie getallen en dit geval staat elke component van deze vector voor de activatiewaarde van een unit u_i op tijdstip t: a_i(t) (zie Jordan 1986 voor een uitgebreide introductie van de algebra van vectoren en matrixen in het kader van PDP-modellen).^1. Bekijk ter illustratie eens het volgende zeer eenvoudige PDP-model met één output unit u die input ontvangt van de n units v: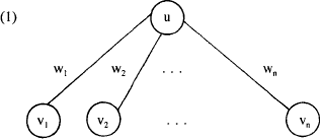

Een n-dimensionale vector v (een vector met n componenten) zal de activatie weergeven van de input units. Elke input unit wordt geassocieerd met een getal dat de activatiewaarde van de unit geeft. Stel dat we vier input units hebben met respectievelijk de activatiewaarden +3, -1, 0, en +2, dan geven we de activatie van deze input units weer als een vector v = [+3, -1, 0, +2]. Elke connectie tussen een input unit en de output unit kan ook geassocieerd worden met een getal: dit getal geeft het gewicht van de connectie. Hoe groter het gewicht, hoe zwaarder of sterker de connectie. De verzameling gewichtjes voor de verschillende connecties in (1) kan ook weer als een vector, de gewichtsvector w, weergegeven worden, bijvoorbeeld w = [+1, +1, -2, +2]. In een model met meer output units heeft elke output unit op die manier zijn eigen gewichtsvector.

Een belangrijke eigenschap van connectionistische modellen is dat kennis is opgeslagen in de connecties tussen de units, en niet in de units zelf. Met andere woorden, we kunnen op een gegeven moment de actieve representatie van een model opslaan als de gewichten van de connecties in het systeem. Met behulp van die opgeslagen gewichten kan dan op elk gewenst moment de representatie opnieuw gecreëerd worden.

1. Activatiewaarden kunnen continu of discreet zijn. Als ze discreet zijn, dan kunnen ze bijvoorbeeld twee verschillende waarden aannemen, zoals 0 of 1. We kunnen in ons voorbeeld de output unit ook zo manipuleren dat er een output waarde 1 gegeven wordt als het inproduct positief is, en een waarde 0 als het inproduct negatief is. Zo'n unit wordt dan wel een drempel unit genoemd. Als activatiewaarden continu zijn, dan kunnen ze elk willekeurig reëel getal aannemen (onbegrensd continu), of bijvoorbeeld elk reëel getal tussen een minimum en een maximum (begrensd).

[p. 106]

Wat we verder nodig hebben bij het specificeren van een PDP-model is een output functie voor elke unit die de staat van activatie op een zeker tijdstip omzet in een output signaal. Stel bijvoorbeeld dat in het model in (1) de activatie van elke input unit wordt vermenigvuldigd met het gewicht van de connectie van deze unit met de output unit, en dat deze producten bij elkaar opgeteld de activatiewaarde van de output unit geven:

(2)	a	u = v.w
	b	u =[+3, -1, 0, +2].[+1, +1, -2, +2] =
		[+3.+1] + [-1.+1] + [0.-2] + [+2.+2] = +6

We berekenen dus een getal u dat de activatiewaarde van de output unit geeft en dat gelijk is wat het inproduct (v.w) van de inputvector en de gewichtsvector genoemd wordt. Het inproduct van twee vectoren geeft een indicatie van hoe dicht de vectoren elkaar naderen. In een eenvoudig PDP-model, zoals hier geschetst, geeft de output activatiewaarde een indicatie van hoe dicht de inputvector de in het systeem opgeslagen gewichtsvector nadert. Het is namelijk zo dat het inproduct groter wordt naarmate twee vectoren dichter bij elkaar liggen.^2. Dat gegeven kunnen we mooi gebruiken. Als we namelijk inputvectoren met een constante lengte achtereenvolgens het model laten passeren, dan zal de output unit het sterkst reageren (d.w.z. met de grootste activatiewaarde) op de inputvector die het dichtst ligt bij de gewichtsvector. Met andere woorden, als een output unit sterk actief wordt, weten we dat de inputvector de in het systeem opgeslagen kennis (in de vorm van de gewichten van de connecties tussen de units) benadert. Als we die gewichten niet kennen, dan kunnen we dus iets leren door verschillende inputvectoren te laten passeren en te kijken welke inputvector de grootste activatiewaarde van de output unit geeft.

Met elke unit u_i is een outputfunctie geassocieerd, f_i(a_i(t)), die de activatiewaarde van de unit, a_i(t), afbeeldt op een output signaal o_i(t) (dus f_i(a_i(t))-=o_i(t)). In sommige modellen zal de outputwaarde exact gelijk zijn aan de activatiewaarde van de unit. In die gevallen is f een identiteitsfunctie (f(x) = x). Het is ook mogelijk dat de outputfunctie f een soort drempelfunctie is, zodat een unit pas effect heeft op een andere unit als de activatiewaarde boven een zekere drempel uitkomt.

We hebben gezien dat units met elkaar verbonden zijn (de connecties). De totale input van een unit kan vaak verkregen worden door eenvoudig de inputs van de binnenkomende units te vermenigvuldigen met het gewicht van de connectie en ze op te tellen. In dat geval kan het totale connectiepatroon weergegeven worden door het gewicht van elke connectie te specificeren. Wanneer er meer output units zijn, kan het handig zijn om zo'n connectiepatroon weer te geven met een matrix W waarbij een knoop w_ij staat voor de zwaarte (het gewicht, een getal) en het type (positief of negatief) van de connectie van unit u_j naar u_i. Matrixen vormen de basis van veel PDP modellen die vectoren als input nemen en vectoren als output leveren, aangezien matrixen verzamelingen vectoren op elkaar afbeelden.

2. Dit is zo omdat het inproduct in verband staat met de hoek tussen twee vectoren, en wel als volgt: v.w = ∥v∥.∥w∥.cosθ, waarbij ∥v∥ de lengte van v geeft, dat is de wortel van het inproduct v.v. Bij een hoek van 90^o is de cosinus 0. Met andere woorden, hoe kleiner de hoek is, hoe groter het inproduct v.w.

[p. 107]

Beschouw bijvoorbeeld een eenlaags PDP-model, dat kan worden weergegeven als in (3):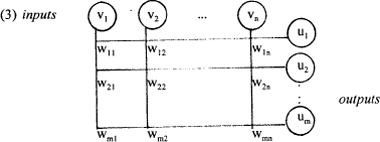

De outputvector u wordt gegeven door u = vW, waarbij de componenten van u de inproducten van v met de horizontale vectoren van W (de rijen van de matrix) zijn. Vermenigvuldiging van een vector en een matrix levert dus een nieuwe vector op. Bijvoorbeeld: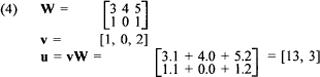

Uit het voorbeeld valt af te lezen dat het product van een n-dimensionale vector v en een m × n matrix W een m-dimensionale vector u oplevert.

Als alle waarden van W en de outputfuncties van de units ingesteld zijn, dan kan een input patroon op een output patroon afgebeeld worden. Vaak is het zo dat neurale netwerken een leerproces ondergaan waarna ze zelf deze waarden kunnen invullen. Dit wordt wel gezien als de belangrijkste eigenschap van connectionistische modellen: het feit dat ze in staat zijn op basis van voorbeelden (input data) een bepaald gedrag te leren. Het doel van zo'n leerproces in PDP-modellen is dus niet het formuleren van expliciete regels, maar de verwerving van de gewichtswaarden van de connecties, waardoor een netwerk zich kan gedragen alsof het de expliciete regels kent. Bij de karakterisering van een PDP-model hoort dus ook de specificatie van een leerregel waarmee connectiepatronen aangepast kunnen worden op basis van ervaring. Vrijwel alle leerregels waarmee de gewichten van connecties kunnen worden aangepast, zijn gebaseerd op Hebb's (1949) eenvoudige regel: Wanneer unit A en unit B gelijktijdig actief zijn, vermeerder dan het gewicht van de connectie tussen A en B. Om ook negatieve activatiewaarden te kunnen verwerken, kan de regel enigszins aangepast worden: Pas het gewicht van de connectie tussen units A en B aan, evenredig met het product van hun gelijktijdige activatie. Ook verfijndere aanpassingsregels van connectiewaarden, waarbij bijvoorbeeld patronen het gewicht van de connecties die ze delen met andere, gelijkende patronen vermeerderen (zoals voorgesteld door Smolensky 1986) hebben als basis deze Hebb-regel.

[p. 108]

2 Concepten en compositionaliteit

Al eerder werd opgemerkt dat over een aantal units gedistribueerde representaties de mogelijkheid bieden om verwante concepten of elementen te representeren als gedeeltelijk overlappende vectoren (denk bijvoorbeeld aan het lettervoorbeeld uit §1). In die zin zijn representaties in de vorm van vectoren alles behalve willekeurig, maar het probleem is dat er niet direct een manier voorhanden is om deze niet-willekeurige structuren systematisch te verwerken in grotere verbanden. Dit wordt vaak gezien als een fatale tekortkoming van connectionisme: het gebrek aan een mechanisme dat op een systematische wijze complexe representaties kan verwerken.

In dit verband kan het nuttig zijn even stil te staan bij Smolensky's (1991) koffie-voorbeeld. Stel dat we de gedistribueerde representatie van kopje met koffie weergeven als de positieve activiteit over een aantal ‘micro-kenmerken’ (om het voorbeeld hanteerbaar te houden, zijn de kenmerken niet echt ‘micro’) zoals o.a.

◊	staand ding waar iets in kan
◊	hete vloeistof
◊	brandgeur
◊	contact tussen bruine vloeistof en porselein
◊	oortje
◊	porseleinen oppervlak
◊	bruine vloeistof in de vorm van een kopje

Tegelijkertijd worden andere units niet geactiveerd, bijvoorbeeld units die staan voor de ‘micro-kenmerken’ ◊ vliegt en ◊ harig. Wat gebeurt er nu als je van deze connectionistische representatie van kopje met koffie de representatie van kopje zonder koffie aftrekt? Onderstaande kenmerken worden dan niet langer geactiveerd:

◊	staand ding waar iets in kan
◊	oortje
◊	porseleinen oppervlak

Dan houd je als het goed is de connectionistische representatie van koffie over. Dat wordt dan:

◊	hete vloeistof
◊	brandgeur
◊	contact tussen bruine vloeistof en porselein
◊	bruine vloeistof in de vorm van een kopje

Het zal duidelijk zijn dat wat we in feite krijgen niet de connectionistische representatie van koffie als algemeen concept is, maar de connectionistische representatie van koffie in de specifieke context van ‘in een kopje’. Met andere

[p. 109]

woorden, de compositionele structuur van kopje met koffie is wel aanwezig, maar deze is niet gelijk aan de context-onafhankelijke representaties van respectievelijk kopje, koffie, en met in een syntactische structuur gecombineerd tot iets als MET (kopje, koffie). Als we het willen hebben over de connectionistische representatie van koffie in dit gedistribueerde schema, dan gaat het in feite over een familie van vectoren, waarbij de representatie van koffie in een context van ‘in een kopje’ een sterke gelijkenis zal vertonen met de representatie van koffie in een context van ‘in een kan’, maar niet exact hetzelfde is.

Het opbreken van een complexe structuur in zijn constituenten kan wel bij benadering worden gedaan in het voorbeeld hierboven, maar is niet precies en uniek gedefinieerd. Smolensky (1991) spreekt in dit verband van zwakke compositionaliteit. De complexe representaties zijn wel degelijk opgebouwd uit de representaties van de delen (ze zijn niet atomair of willekeurig, zoals Fodor and Pylyshyn 1988 beweren), maar een precieze formalisatie blijft voorlopig achterwege.

Hiermee hebben we dus nog niet een manier gevonden om complexe structuren te representeren en te manipuleren op een structuurgevoelige wijze, terwijl het belang daarvan zowel door tegenstanders van connectionistische benaderingen (met name Fodor en Pylyshyn 1988) als door Smolensky (1991) wordt ingezien. Smolensky houdt vol dat gedistribueerde representaties compositioneel kunnen zijn zonder dat ze gebruik maken van mentale syntactische structuren (de Language of Thought). Een niet-willekeurige representatie van een complex gestructureerd object kan met andere woorden een betekenisvolle structuur hebben die niet gelijk staat aan een strikt syntactische structuur. Als we symbolische verwerking in een PDP-model willen inbedden, dan is de vraag hoe vectoren gebruikt kunnen worden bij de representatie van symbolische structuren en hoe PDP-netwerken structuurgevoelige verwerking kunnen bereiken. Er zijn de laatste tijd verschillende technieken ontwikkeld waarmee complex gestructureerde objecten wel in connectionistische systemen geïmplementeerd kunnen worden, en een van de belangrijkste is Smolensky's tensorproduct-theorie (zie o.a. Smolensky 1991, 1995).

Volgens Smolensky komt het probleem in feite neer op het vinden van een afbeelding van een verzameling gestructureerde objecten (bijvoorbeeld taalkundige bomen) op een verzameling vectoren waarbij de verschillende relaties tussen de constituenten bewaard moeten blijven, in die zin dat een representatie van een complex object gegenereerd kan worden als een combinatie van de representaties van de delen, maar ook dat die delen weer teruggevonden kunnen worden, als men dat wenst.

Van Gelder (1990) betoogt in overeenstemming daarmee dat het verschil tussen klassieke, symbolische benaderingen en connectionisme niet gelegen is in het verschil tussen gestructureerde en ongestructureerde representaties, zoals vaak beweerd wordt (o.a. Fodor en Pylyshyn 1988), maar in twee verschillende benaderingen van het begrip compositionaliteit. De gebruikelijke compositionele systemen die wij kennen zijn allemaal aaneenschakelend in de zin dat een complexe expressie de verschillende constituenten letterlijk bewaart in de expressie zelf. De constituenten worden geordend zonder dat er iets aan

[p. 110]

veranderd wordt, zoals in het voorbeeld: Als A en B welgevormde expressies zijn, dan is A&B een welgevormde expressie. A is hier onveranderd aanwezig in de complexe expressie A&B en ook direct zichtbaar. Formele talen uit de wiskunde, logica en informatica zijn allemaal compositioneel in deze zin, evenals natuurlijke talen in geschreven vorm (in gesproken taal veranderen woorden wel degelijk qua klank, afhankelijk van de context). Van Gelder beargumenteert dat dergelijke aaneenschakelingen weliswaar altijd compositioneel zijn, maar dat het omgekeerde niet geldt. Dat wil zeggen, er bestaat ook functionele compositionaliteit zonder aaneenschakelingen. Smolensky's tensorproduct-representaties zijn namelijk functioneel compositioneel zonder aaneenschakelend te zijn. Oftewel, de representatie van een complex object kan eenduidig worden opgebouwd uit de representaties van de delen, waarbij de delen ook weer terug te vinden zijn indien men dat wil, maar zonder dat die delen letterlijk aanwezig of zichtbaar zijn in de representatie van het complexe object. Smolensky (1995) merkt wel op dat het semantische principe van compositionaliteit dat de betekenis van een complexe expressie afleidt van de betekenissen van de delen en de syntactische structuur in deze benadering nog steeds gestipuleerd moet worden, net als in klassieke benaderingen.

3 Tensorproducten

Het spreekt vanzelf dat het simpelweg optellen van vectoren (een gebruikelijke operatie in connectionistische modellen) niet functioneel compositioneel is. Weliswaar kunnen we een complex object genereren als we de representaties van de delen kennen (bijvoorbeeld, u+v = [1, 2, 3] + [4, 5, 7] = [5, 7, 9], maar de delen waaruit deze complexe vector u+v is opgebouwd zijn niet terugvindbaar als we dat willen (immers, [5, 7, 9] is net zo goed de som van twee vectoren p = [2, 6, 3] en q = [3, 1, 6]). Smolensky komt daarom op het idee om de machtiger operatie van tensorproduct-formatie te gebruiken. Het tensorproduct van een n-dimensionale vector u en een m-dimensionale vector v is de n×m-dimensionale vector w waarvan de componenten bestaan uit alle paarsgewijze producten van de componenten van u en v (het tensorproduct van u en v in het voorbeeld hierboven is dus de negendimensionale vector w = u⨂v = [4, 8, 12, 5, 10, 15, 7, 14, 21]). Een tensorproduct van twee vectoren lijkt op het meer bekende uitproduct van twee vectoren, maar het voordeel van tensorproducten is dat het resultaat zelf weer een vector is (bij uitproducten is dat een matrix), waardoor tensorproduct-formatie recursief kan worden toegepast (tensorproducten kunnen zelf ook weer bij vectoren opgeteld worden, of tensorproducten met andere vectoren vormen).^3.

Met Smolensky's idee om tensorproduct-formatie te gebruiken, is het doel nog niet bereikt. Smolensky's andere minstens zo belangrijke idee is om gestructureerde objecten op te breken in plaatsen/rollen (roles) en plaats- of rolbezetters (fillers). Laten we eens bekijken hoe dit idee van decompositie in combinatie met tensorproduct-formatie toegepast kan worden om recursieve symbool structuren, zoals taalkundige bomen, te definiëren in ICS. Smolensky

3. We hebben gezien dat voor een algemene m×n matrix W en een n-dimensionale vector v het product Wv een m-dimensionale vector u oplevert, waarvan de componenten gegeven worden door de inproducten van v met de horizontale vectoren van W. Het product van twee matrixen is alleen gedefinieerd als het aantal kolommen van de eerste matrix gelijk is aan het aantal rijen van de tweede matrix; vermenigvuldiging van een r×s matrix en een s×t matrix levert een r×t matrix op. Het omgekeerde van een n×m matrix W is een m×n matrix die geschreven wordt als W^T. Een vector [1, 2, 3] kan net zo goed een matrix met één kolom genoemd worden. Het omgekeerde van een n-dimensionale vector v levert een matrix met een rij v^T op. Het product v^Tu (waarbij u elke n-dimensionale vector kan zijn) is een getal, dat gelijk is aan het inproduct van de vectoren v en u (ga na). Nemen we nu het product uv^T, dat een legaal product is omdat het aantal kolommen in u overeenkomt met het aantal rijen in v^T, dan is het resultaat niet een getal, maar een n×n matrix. Een product van de vorm uv^T wordt het uitproduct van de vectoren u en v genoemd.

[p. 111]

gaat uit van binary branching (bomen zijn altijd tweevertakkend), waarbij twee onderling onafhankelijke primitieve vectoren r₀ en r₁ de linker- en rechtertakrollen representeren.^4. De complexe structuur [Petra [schaduwt Els]] wordt als volgt gerealiseerd door een vector a: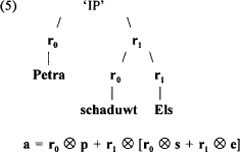

In bovenstaand voorbeeld denoteren p, s, en e de representaties voor Petra, schaduwt en Els, respectievelijk. Tensorproducten binden dus steeds een rol (de linker- of de rechtertak in de boom) aan een vector die de constituent representeert die die rol vervult (oftewel, die op die plaats in de boom staat). De resulterende tensorproduct-vectoren worden bij elkaar opgeteld en leveren aldus de vector voor het gehele gestructureerde object. Omdat r₀ en r₁ onafhankelijke vectoren zijn, elk geassocieerd met één specifieke rol, kan elke complexe tensorproduct-representatie van deze vorm teruggebracht worden tot de twee vectoren waaruit ze is opgebouwd: dit kunnen namelijk niet twee willekeurige vectoren zijn. Ze moeten respectievelijk van de vorm r₀⨂x en r₁⨂y zijn, en er is maar een mogelijkheid als r₀ en r₁ onafhankelijk van elkaar zijn. Op deze manier kan de hele structuur van een complex object teruggevonden worden, als men dat zou willen.

Smolensky (1991, noot 13, p.227) doet uit de doeken hoe hij op het idee gekomen is om tensorproducten te gebruiken om gedistribueerde representaties voor complexe objecten op te bouwen uit de representaties van hun delen en de representaties van de rollen die deze delen bezetten. Hij bespreekt daartoe de relatie tusen de representatie van een electron en een atoom in moderne natuurkunde. Een atoom als geheel wordt gerepresenteerd door een vector die de som is van vectoren die elk een specifiek electron in zijn orbitaal representeren. Met andere woorden, de vector die het geheel representeert is de som van de tensorproducten van paren vectoren die de bezetter en de rol onafhankelijk van elkaar representeren. Het lijkt redelijk om electronen in die zin als ‘constituenten’ van atomen te bestempelen. Zijn de constituenten werkelijk aanwezig als je ze niet meteen kunt zien, maar eerst een operatie moet toepassen om ze terug te vinden? Smolensky (1991, p.227): ‘We can analyze the system by breaking up the vector for the whole into vectors for the parts, and in general that's a good way to do the analysis; but nature doesn't do that in updating the state of the system from one moment to the next.’

Smolensky (1991) noemt zijn tensorproduct-representaties sterk compositioneel, in tegenstelling tot de zwakke compositionaliteit van het koffievoorbeeld

4. Vectoren zijn onderling onafhankelijk als geen van hen herschreven kan worden als de lineaire combinatie van de andere. De vectoren [1, 2] en [3, 6] bijvoorbeeld zijn afhankelijk omdat [3, 6] = 3.[1, 2]. De vectoren [1, 0] en [0, 1] zijn daarentegen onafhankelijk.

[p. 112]

uit §1, omdat de constituenten gebonden zijn aan specifieke structurele rollen. Dit gold niet voor de elementen waaruit de representatie van kopje met koffie was opgebouwd. Deze elementen waren weliswaar gelijktijdig aanwezig, maar niet aan syntactische rollen gebonden. Smolensky's ICS (zie §0) past sterke compositionaliteit toe: symbolische representaties worden gerealiseerd via tensorproduct-formatie. Grammatica's worden beschouwd als functies die symbolische inputstructuren afbeelden op symbolische outputstructuren. In ICS worden inputs en outputs gerealiseerd als tensorproduct-representaties, en connectionistische verwerking wordt gebruikt om de outputs te berekenen op grond van de inputs.

4 Harmonieuze grammatica

Smolensky's tensorproduct-representaties vormen samen met de notie relatieve welgevormdheid, oftewel harmonie, de basisideeën van zijn theorie van taal en grammatica. Het samenbrengen van het begrip welgevormdheid uit de taalkunde en het begrip welgevormdheid (harmonie) uit het connectionisme levert een interessante en vruchtbare nieuwe benadering van grammatica op.

De relatieve welgevormdheid of harmonie van een activatievector in een connectionistisch netwerk is een numerieke maat die aangeeft in hoeverre de vector welgevormd is met betrekking tot een verzameling welgevormdheids-condities (die als kennis in het systeem opgeslagen zijn) (Smolensky 1986, 1995). Bekijk eens een heel eenvoudig voorbeeld (vergelijkbaar met (1) uit §1):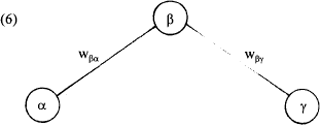

Stel dat in dit voorbeeld de connectie van α naar β een negatief gewicht heeft van -6: w_βα=-6. Zo'n connectie kan opgevat worden als een conditie: als α actief is, dan mag β dat niet zijn. Op dezelfde manier kan de connectie van γ naar β opgevat worden als een positieve conditie indien w_βγ=+3. Deze laatste conditie is zwakker dan de eerste, omdat het gewicht kleiner is. Als α en γ beide actief zijn, dan is β dus blootgesteld aan twee conflictueuze condities. Als ze precies even actief zijn (hun activatiewaarden zijn gelijk), dan zal de sterkste (de negatieve in dit geval) winnen.

Stel dat we een activatiepatroon x hebben waarin zowel α als β actief zijn, met respectievelijk de activatiewaarden 1 en 2. De conditie Als α actief is, dan mag β dat niet zijn wordt dan geschonden en het getal van de negatieve harmonie kan als volgt berekend worden:

[p. 113]

(7)	Hβα(x) = aβwβαaα = 2.-6.1 = -12

In (7) hebben we de harmonie van x met betrekking tot één connectie, de connectie van α naar β, berekend. Als nu bijvoorbeeld de activatiewaarde van γ in x gelijk is aan 1, dan kunnen we ook H_βγ berekenen (in (8a)) en vervolgens de totale harmonie van x (in (8b)):

(8)	a	Hβγ(x) = aβwβγaγ = 2.3.1 = 6
	b	Hβα(x) + Hβγ(x) = -6

We zien dat het activatiepatroon x voldoet aan de zwakkere conditie, maar tegelijkertijd de sterkere conditie schendt, wat in dit geval leidt tot een negatieve harmonie. Als we een patroon y zouden bekijken dat gelijk is aan x, behalve dat a'_β gelijk is aan -2, dan zien we dat dit patroon de zwakkere conditie schendt en voldoet aan de sterkere, en de harmonie van dit patroon is gelijk aan +6. We kunnen daarom zeggen dat y welgevormder is dan x met betrekking tot deze twee condities (omdat de harmonie van y groter is dan de harmonie van x).

De totale harmonie van een activatiepatroon x in een netwerk met een gewichtsmatrix W is de som van de harmoniewaarden van x met betrekking tot alle individuele connecties:

(9)	DEF.	De welgevormdheid of harmonie van een activatievector x is:
		H(x) = ΣβαHβα = Σβαaβwβαaα = x^TWx

In ons voorbeeld was y harmonieuzer dan x, wat min of meer betekent dat een activatiestroom eerder y zal genereren dan x, om op die manier een activatiepatroon te creëren met maximale harmonie. Dit proces waarbij de spreiding van activatie resulteert in een patroon met maximale harmonie, wordt door Smolensky harmonie- maximalisering genoemd, oftewel parallelle voldoening aan zachte condities (de condities worden zacht genoemd omdat ze overstemd kunnen worden door sterkere condities). Harmonie-maximalisering is een essentieel theorema in ICS omdat het voorziet in een manier om op een hoger niveau van analyse te redeneren over cognitieve processen. Laat me dit toelichten.

Stel dat we een inputvector opleggen aan een PDP-model. Deze inputvector blijft onveranderd aanwezig gedurende de verwerking en maakt deel uit van de totale staat van activatie: de inputvector i is een deel van de activatievector x, omdat de input units deel uitmaken van de totale verzameling processing units in het netwerk. We kunnen x opvatten als een vervolmaking van de inputvector i. De outputvector o is op dezelfde wijze een onderdeel van het totale activatiepatroon x, omdat de componenten van de outputvector gegeven worden door de activatiewaarden van de output units, die eveneens weer deel uitmaken van de totale verzameling processing units. Met andere woorden, een gedeelte van de vervolmaking van een inputvector i tot een activatiepatroon x kan opgevat worden als een functie f die de input i op een

[p. 114]

optimale (meest harmonieuze) output o afbeeldt. Smolensky noemt een aantal eigenschappen waaraan een PDP-model moet voldoen, wil het een harmonieus netwerk genoemd worden (zie Smolensky 1995). Een en ander leidt tot het theorema van harmonie-maximalisering dat als volgt geformuleerd kan worden:

(10)	Harmonie-maximalisering (THEOREMA):
	In harmonieuze netwerken zal op ieder moment van verwerking de harmonie van het totale activatiepatroon stijgen of gelijk blijven. Verder is het zo dat voor een uitgebreide verzameling activatieregels, de activatie zich uiteindelijk installeert (settles) als de vector (uit de verzameling vectoren x die als vervolmakingen van de input i beschouwd kunnen worden) die H(x) maximaliseert.

Hiermee kunnen we op basis van een symbolische inputstructuur I een symbolische outputstructuur O specificeren, zonder dat we hoeven te refereren aan het connectionistische niveau van activatievectoren en gewichtsmatrixen:

(11)

Harmonieuze grammatica kent aan iedere gegeven symbolische structuur I een output symbolische structuur O toe (die een element is van de verzameling mogelijke outputstructuren voor I) waarvan de harmonie of welgevormdheid maximaal is. Verder geldt dat hoe hoger de uiteindelijke harmoniewaarde van O is, hoe welgevormder I, volgens de grammatica.

Van dit laatste principe (hoe hoger H, hoe welgevormder I) zullen we een voorbeeld zien in de toepassing van harmonieuze grammatica op het gebied van Franse onaccusatieven in de volgende subparagraaf. Het is niet moeilijk nu al in te zien dat een dergelijk principe ook de verklaring van graduele welgevormdheidsoordelen mogelijk maakt (stel bijvoorbeeld dat H(x)=0 een grammaticaliteitsoordeel ? voor I betekent).

Een harmonieuze grammatica specificeert dus een input/output functie zodanig dat de output de vervolmaking van de input is die de harmoniefunctie maximaliseert of optimaliseert. Vandaar dat deze meest welgevormde output optimaal genoemd wordt met betrekking tot de input, waarmee ook de benaming voor de niet-numerieke opvolger van harmonieuze grammatica, Optimality Theory, alvast verklaard is.

De harmoniefunctie van een systeem vangt de kennis van dat systeem in een verzameling conflictueuze, zachte condities van variërerende sterkte. Een harmonieuze grammatica kan daarom opgevat worden als een verzameling zachte welgevormdheids-condities. Dat deze condities zacht zijn, heeft verreikende consequenties: als alle mogelijke outputstructuren de sterkste conditie schenden, dan telt deze conditie niet mee bij de beslissing welke outputstructuur het meest welgevormd is. Oftewel, een outputstructuur kan nooit verworpen worden omdat er te veel of te belangrijke condities geschonden worden; een outputstructuur kan slechts om een reden verworpen worden, en dat is: er

[p. 115]

is een betere outputstructuur voorhanden in de verzameling van mogelijke outputstructuren.

Het is wellicht niet overbodig erop te wijzen dat de mogelijke outputstructuren met betrekking tot een gegeven input (de zogenaamde kandidatenverzameling) niet één voor één door het netwerk getest worden om te kijken welke optimaal is. De verzameling mogelijke outputstructuren kan in principe oneindig zijn, maar de parallelle verwerking van de input met betrekking tot de in het systeem opgeslagen condities, zorgt ervoor dat de harmonie van het totale activatiepatroon alleen maar stijgt tot het een zeker maximum bereikt waarop de vector zich installeert (zie het theorema van harmonie-maximalisering in (10)). Het één voor één bekijken van mogelijke kandidaten is een proces dat wij (als buitenstaanders) kunnen uitvoeren om bijvoorbeeld te analyseren hoe het connectiepatroon er uit moet zien waarmee het netwerk, gegeven een bepaalde input, tot een bepaalde output komt.

4.1 Een toepassing: Franse onaccusatieven

Een bekende klassificatie die een grote rol blijkt te spelen bij uiteenlopende taalkundige data is de onderverdeling van intransitieve werkwoorden in enerzijds onaccusatieve oftewel ergatieve werkwoorden, en anderzijds onergatieve werkwoorden. Subjecten van de onaccusatieve klasse werkwoorden doen in gedrag vaak denken aan objecten van transitieve werkwoorden. Daarom wordt wel aangenomen dat subjecten van onaccusatieve werkwoorden op het niveau van D-structuur direct object zijn van het werkwoord, oftewel intern argument, terwijl subjecten van onergatieve werkwoorden ook basisgegenereerd zijn als subjecten, oftewel externe argumenten. Laten we een concreet voorbeeld bekijken. Een van de tests in het Frans om te bepalen of een werkwoord onaccusatief is of niet, heeft betrekking op het gedrag van het betreffende werkwoord in een zogenaamde Object Raising context. Objecten van transitieve werkwoorden kunnen naar voren geplaatst worden in bepaalde contexten (zie (12a)) in tegenstelling tot subjecten van transitieve werkwoorden (zie (12b)). Voor onaccusatieve werkwoorden geldt dat subjecten zich gedragen als de objecten van transitieve werkwoorden en wel verplaatst kunnen worden ((12c)), terwijl de subjecten van onergatieve werkwoorden zich gedragen als de subjecten van transitieve werkwoorden, waarvoor verplaatsing niet mogelijk is ((12d)):

(12)	a	La vérité est facile à faire dire aux enfants
	b	*Les enfants sont faciles à faire dire la verité
	c	La glace est facile à faire fondre
	d	*Les étudiants sont faciles à faire travailler

Voor het Nederlands zijn er drie welbekende tests om uit te vinden of een bepaald intransitief werkwoord tot de klasse van onaccusatieven dan wel tot de klasse van onergatieven behoort. Ten eerste kan men kijken naar de hulpwerk-

[p. 116]

woord selectie van het werkwoord; onaccusatieven selecteren als hulpwerkwoord zijn, onergatieven hebben:

(13)	a	Petra is gearriveerd / gevallen
	b	Petra heeft gelachen / geslapen

Ten tweede zijn onpersoonlijke passiefconstructies alleen mogelijk met onergatieve werkwoorden:

(14)	a	*Er wordt gearriveerd / gevallen
	b	Er wordt gelachen / geslapen

En ten derde zijn adjectivale ge-deelwoorden alleen mogelijk met onaccusatieve werkwoorden:

(15)	a	de zojuist gearriveerde trein / de gevallen jongen
	b	*de gelachen / geslapen jongen

Dit laatste komt overeen met het gebruik van ge-deelwoorden van transitieve werkwoorden; deze hebben ook altijd betrekking op het object of interne argument van het werkwoord en niet op het subject of externe argument:

(16)	de gewurgde man

Immers, de constructie in (16) kan alleen maar verwijzen naar de man die gewurgd werd, niet naar de man die wurgde.

Uit bovenstaande drie tests valt af te leiden dat de Nederlandse werkwoorden arriveren en vallen onaccusatief zijn, terwijl lachen en slapen tot de onergatieve werkwoorden gerekend kunnen worden. In de literatuur is vaak beweerd dat niet alledrie deze tests even betrouwbaar zijn. Zaenen (1993) beargumenteert bijvoorbeeld dat de tweede test niet geschikt is om onaccusativiteit te testen, omdat de mogelijkheid om onpersoonlijke passieven te gebruiken afhangt van de aspectuele eigenschappen van de hele zin. Hoekstra en Mulder (1990), echter, gebruiken juist deze test voor het klassificeren van onaccusatieve en onergatieve werkwoorden, en betogen dat de eerste test niet betrouwbaar is, omdat niet alle ergatieve werkwoorden zijn selecteren.

Voor het Frans valt een soortgelijke onduidelijkheid waar te nemen. Legendre (1989) onderscheidt maar liefst tien tests om te bepalen of een intransitief werkwoord onaccusatief of onergatief is, en deze tests blijken maar zeer ten dele te overlappen: het ene werkwoord komt bij alle tien de tests als onaccusatief uit de bus; het andere slechts bij eentje. Op basis hiervan zou Legendre kunnen stellen dat het ene werkwoord onaccusatiever is dan het andere, maar in plaats daarvan betoogt ze dat een werkwoord onaccusatief is als het zich onaccusatief gedraagt in tenminste één van de tien tests. Een dergelijke regel is niet toereikend om juist de complexe overlappingen in

[p. 117]

klassificaties te verklaren, die het ene werkwoord in meer contexten onaccusatief maken dan het andere.

Dit is nu juist wat een connectionistisch netwerk gebaseerd op harmonieuze grammatica heel goed kan (Legendre, Miyata, en Smolensky 1990a,b). In plaats van het gebruik van twee mogelijkheden (onaccusatief of ergatief) en harde condities die op dit onderscheid gebaseerd zijn, biedt de connectionistische benadering van Legendre et al. de mogelijkheid om zowel syntactische als semantische neigingen of voorkeuren te formaliseren als zachte condities. Daarmee kan vrijwel het hele, complexe patroon van data beschreven worden en wordt een voor de hand liggende verklaring geboden voor enerzijds het graduele karakter van onaccusatieve/onergatieve categorieën (het feit dat sommige werkwoorden ‘onaccusatiever’ zijn dan andere) en anderzijds het graduele karakter van de grammaticaliteitsoordelen in verschillende contexten.

Het doel van Legendre et al. is niet om de taalkundige data uitgebreid te bespreken, maar slechts om te laten zien hoe harmonieuze grammatica toegepast kan worden om deze data te verklaren. De algemene methodologie is als volgt. Harde welgevormdheidscondities van de vorm (17a) uit de taalkunde, kunnen vervangen worden door zachte welgevormdheids-condities van het type (17b):

(17)	a	Schending van conditie X levert een ongrammaticale structuur op
	b	Schending van conditie X vermindert de welgevormdheid van de structuur met een constante CX

De constanten C_X in de zachte regels van harmonieuze grammatica zouden het formalisme hopeloos log maken (het is ondoenlijk om als theoreticus de precieze getalletjes uit te dokteren, waar deze constanten voor staan), ware het niet dat een goed connectionistisch netwerk deze getallen zelf kan berekenen op basis van taalkundige data en een geschikte leerregel (zie §1).

Een verzameling relevante kenmerken wordt geïdentificeerd om de taalkundige structuren uit de dataverzameling te beschrijven en hierop gebaseerde zachte welgevormdheidscondities worden als connecties in een netwerk geïmplementeerd. Het netwerk krijgt als input gecodeerde taalkundige structuren aangeboden, en produceert als output een getal dat geïnterpreteerd kan worden als een maat van welgevormdheid, een acceptabiliteitsoordeel. Vervolgens wordt het netwerk getraind met de verzameling linguïstische data. Het doel hiervan is het vinden van de juiste gewichten van de connecties, die dan weer geïnterpreteerd kunnen worden als de constanten C_X in de regels (17b). Het netwerk krijgt de input (gecodeerde (tensorproduct-representaties van)) linguïstische structuren en de gewenste output (de doelwaarden die overeenstemmen met de acceptabiliteitsoordelen van informanten met betrekking tot de inputstructuren) aangeboden, en moet op basis hiervan zelf de connecties gaan invullen/bijstellen. Dit wordt het trainen of leren van het netwerk genoemd.^5. Het leren van een netwerk kan vaak beschreven worden als het vinden van een zodanige aanpassing van de gewichten van de connecties dat het netwerk de volgende keer dat het netwerk hetzelfde patroon tegenkomt een iets kleinere

5. In dit geval gaat het om gesuperviseerd leren, omdat bij elke input ook de gewenste output gegeven wordt. Bij ongesuperviseerd leren krijgt een netwerk alleen maar de input en moet dan bijvoorbeeld zelf leren om op elkaar gelijkende patronen in dezelfde klasse af te beelden.

[p. 118]

fout maakt in het afbeelden van de input op de output (wat inhoudt dat het verschil tussen de outputwaarde die het netwerk berekent en de gegeven doelwaarde van de output kleiner wordt). Bedenk dat elke gewichtswaarde in het netwerk een variabele is die de gemaakte fout kan beïnvloeden. Gewichtswaarden kunnen worden aangepast met een leerregel die aangeduid wordt als de delta-regel of gradient descent leerregel (zie Rumelhart et al. 1986). Daarmee wordt de fout die het netwerk maakt, na elke aanpassing een beetje kleiner. Met een standaard back propagation algoritme worden patronen vergeleken en wordt het verschil tussen de doelwaarde en de door het netwerk gerealiseerde waarde met behulp van de delta-regel geminimaliseerd. Het trainen van het netwerk is dus een computationele procedure om de numerieke constanten C_X in de zachte condities van de vorm (17b) in te vullen. Als we die waarden hebben gevonden, dan kunnen we het netwerk analyseren, waarmee een bijdrage geleverd kan worden aan de analyse en theorievorming op een hoger, taalkundig niveau van beschrijving.

Legendre et al. gebruiken 760 input zinnen, die alle gecodeerd zijn met betrekking tot vier aspecten: context (er zijn vier mogelijke contexten, o.a. de Object raising context), semantische kenmerken van het argument (2 kenmerken, te weten volitionality ‘controleerbaarheid, opzettelijkheid’ en animacy ‘leven’), semantische kenmerken van het predikaat (te weten, teliciteit en progressiviteit) en het individuele werkwoord dat in de zin gebruikt wordt (er zijn 143 mogelijke werkwoorden). Deze vier aspecten leveren 151 variabelen op (4+2+2+143) die ieder een eigen input unit krijgen in het netwerk (als een context unit de waarde 1 krijgt, dan krijgen de andere drie 0; de vier units die de semantische kenmerken representeren, krijgen elk een waarde tussen 0 en 1; van de units voor de individuele werkwoorden, krijgt er een de waarde 1, en de andere 142 krijgen de waarde 0). Het structurele kenmerk D-structuur subject/D-structuur object wordt niet expliciet in de input zin gerepresenteerd. Voor dit kenmerk maakt het netwerk gebruik van twee hidden units, een voor beide mogelijkheden. De 151 input units die de vier aspecten van de gecodeerde input zinnen representeren hebben allemaal een directe connectie met de hidden units. Omdat de twee hidden units twee complementaire structurele eigenschappen representeren, mag alleen de hidden unit met de hoogste activatiewaarde (de winnaar) zijn activatiewaarde doorsturen naar de output unit.

Verder zijn er conjunctie-units die de zachte condities representeren (bijvoorbeeld, Als de Object raising context-unit actief is, dan moet de hidden unit die het D-structuur object representeert ook actief zjn): in totaal zijn dat er 175 (32 hiervan representeren algemene grammaticale condities zoals die in het voorbeeld; de 143 andere representeren de lexicale voorkeuren van individuele werkwoorden voor het structurele kenmerk D-structuur subject/D-structuur object - deze condities kunnen geïnterpreteerd worden als een lexicale markering van de werkwoorden voor het kenmerk onaccusatief/onergatief).

De totale input van de output unit is de som van de bijdragen van de conjunctie-units, de context units en de winnende hidden unit. De outputfunctie

[p. 119]

van de output unit is een monotoon stijgende, sigmoïde functie (f(x) = 1/1+e^-x), die de totale input afbeeldt op een waarde tussen 0 en 1. Deze waarde kan geïnterpreteerd worden als een schatting van de welgevormdheid van de input zin.^6.

Na training maakte het netwerk slechts twee grote fouten in de schatting van de welgevormdheid van de 760 zinnen (bijvoorbeeld, de outputwaarde van het netwerk was 0.7 = +?, terwijl het welgevormdheidsoordeel van de informanten 0.3 = -? was). De gewichten van de zachte condities konden dus met succes automatisch bepaald worden, waarna een taalkundige analyse van het netwerk kon plaatsvinden.

Een benadering zoals hier uiteengezet, is veelbelovend, omdat zowel syntactisch als semantisch gemotiveerde welgevormdheidscondities en bovendien condities met betrekking tot de relatie tussen syntaxis en semantiek te zamen een complex patroon van data en welgevormheidsoordelen kunnen verklaren.

Wat pure connectionisten tegen hebben op een model als dit, is dat er zoveel door theoretici geknutseld wordt. Het aantal mogelijke condities (conjuncties tussen input units) wordt bijvoorbeeld sterk gereduceerd tot een verzameling taalkundig gemotiveerde condities, waardoor het niet meer duidelijk is hoe een netwerk automatisch dezelfde resultaten zou kunnen bereiken op basis van alleen input data en connectionistische leerregels. Dat hoeft natuurlijk ook niet volgens Smolensky. Harmonieuze grammatica bevat een verzameling universele condities die niet aangeleerd hoeven te worden, maar die deel uitmaken van een aangeboren component Universele Grammatica. Deze condities zelf hoeven niet geleerd te worden op basis van de input data, alleen hun gewichten (in harmonieuze grammatica) of hun rangschikking (in OT). Het idee van een universele verzameling welgevormdheidscondities is niet nieuw in de taalkunde, maar het feit dat deze condities zacht zijn, brengt een taalkundige theorie binnen handbereik (namelijk harmonieuze grammatica of Optimality Theory) waarin noties als gemarkeerdheid, relatieve welgevormdheid, en syntactische en semantische voorkeuren met succes deel uit gaan maken van de kern van de theorie en niet langer verbannen worden naar de periferie.

6. Het hoog(-cognitief)-niveau netwerk dat hier beschreven wordt, is afgeleid van een laag(-cognitief)-niveau netwerk en is daarmee isoharmonieus, zoals aangetoond door Legendre et al. (1990a): de lokale units in het hoog-niveau netwerk corresponderen met gedistribueerde representaties in het laag-niveau netwerk en de harmonie van corresponderende toestanden in de twee netwerken is gelijk.

5 Optimality Theory

Optimality Theory (OT) kan beschouwd worden als een niet-numerieke variant en opvolger van harmonieuze grammatica. Smolensky (1995): ‘Phonological applications of harmonic grammar led Alan Prince and myself to a remarkable discovery: in a broad set of cases, at least, the relative strengths of constraints need not be specified numerically.’ Met andere woorden, op het moment dat de gewichten van de connecties bekend zijn, kan een ordening van sterk naar zwak aangebracht worden in de condities, die een numerieke specificatie overbodig maakt. Het blijkt namelijk, dat de gewichtswaarden zo liggen dat elke conditie sterker is dan alle zwakkere condities te zamen, oftewel: Condi-

[p. 120]

ties kunnen nooit overstemd worden door zwakkere condities, hoeveel dat er ook zijn. Condities kunnen daarom ondergebracht worden in strikte dominantie-hiërarchieën die het specificeren van expliciete gewichtswaarden overbodig maken voor taalkundige analyse.

Wanneer taalkundigen als onderdeel van UG een universele verzameling van conflictueuze condities weten te formuleren, dan kan cross-linguïstische variatie in de rangschikking van deze condities een verklaring bieden voor de verschillende wijzen waarop talen de conflicten tussen de condities oplossen, d.w.z. hoe het kan dat talen verschillen in wat de optimale output voor een gegeven input is. Deze manier om taaltypologische verschillen te analyseren als het resultaat van alternatieve rangschikking in dominantie-hiërarchieën, biedt volop mogelijkheden voor verklaringen en voorspellingen van mogelijke patronen in natuurlijke talen. Dit kan het best geïllustreerd worden aan de hand van een concreet voorbeeld van een dergelijke studie in de volgende subparagraaf.

5.1 Een toepassing: Casus-systemen

De notie ergativiteit wordt niet alleen gebruikt voor een bepaald type intransitieve werkwoorden (de onaccusatieve of ergatieve werkwoorden uit §4.1), maar in de eerste plaats voor een bepaald type talen waarin de Casusdistributie zodanig is dat objecten van transitieve werkwoorden samen met subjecten van intransitieve werkwoorden een natuurlijke klasse vormen. In talen als het Nederlands en het Engels (ook wel nominatieve talen genoemd) krijgen subjecten van transitieve en intransitieve zinnen beide nominatieve Casus, terwijl objecten van transitieve zinnen accusatieve Casus ontvangen. In ergatieve talen daarentegen, dragen subjecten van transitieve werkwoorden ergatieve Casus, terwijl subjecten van intransitieve werkwoorden dezelfde Casus ontvangen als objecten van transitieve werkwoorden, namelijk absolutieve Casus. Een voorbeeld uit de ergatieve taal Yup 'ik (een Inuit-taal, gesproken in Alaska):^7.

(18)	a	Angutem tangrr-aa arnaq
		manERG ziet vrouwABS
		‘De man ziet de vrouw’
	b	Arnaq yruar-tuq
		vrouwABS danst
		‘De vrouw danst’

In de generatieve literatuur zijn verschillende analyses bekend die het verschil tussen nominatieve en ergatieve talen trachten te verklaren. In een wat traditionelere analyse wordt de nominatieve Casus in nominatieve talen gelijkgesteld aan de absolutieve Casus in ergatieve talen: beide zijn altijd aanwezig op een of ander argument in elke finiete zin, en beide hebben de neiging de morfologisch minst gemarkeerde Casus te zijn in de verschillende talen. Van recentere

7. Alle voorbeelden uit Inuit-talen in deze paragraaf zijn overgenomen uit Bok-Bennema (1991).

[p. 121]

oorsprong zijn analyses die nominatieve Casus gelijkstellen aan ergatieve Casus (beide zijn het ‘hoogst’ in de boom) en accusatieve aan absolutieve (Bobaljik 1992, Chomsky 1992, Laka 1993).

In Legendre, Raymond en Smolensky (1993) worden nominatieve en ergatieve Casus ook samen genomen onder de noemer C₁, en accusatieve en absolutieve Casus als C₂. Een derde type abstracte Casus, C₄, wordt eenvoudigweg gebruikt voor alle typen lagere Casus, zoals oblique Casus, maar ook voor argumenten die impliciet blijven. Het doel van Legendre, Raymond en Smolensky is te verklaren hoe verschillende taalsystemen bepaalde argumentstructuren afbeelden op optimale Casus-realisaties in de outputstructuur. Als input nemen ze eenvoudige predikaat-argumentstructuren, waarbij elk argument in de input gelabeld is met zijn thematische rol (in dit artikel worden alleen A=agent en P=patient als mogelijke labels gebruikt) en of het argument hoog of laag prominent is in het discussiedomein. Hoge prominentie wordt weergegeven met een hoofdletter; lage met een kleine letter. Al met al zijn intransitieven dus gelabeld als A of P, transitieven als AP, passieven als aP, en antipassieven als Ap (voorbeelden volgen later in de tekst). De output die door een grammatica wordt toegekend aan een input bestaat uit de input argumenten zelf plus een waarde voor ieder argument dat de abstracte Casus van dat argument weergeeft (-₁, -₂ of -₄). Een bijkomende assumptie is dat kandidatenverzamelingen van mogelijke outputs niet toestaan dat twee argumenten in één structuur dezelfde kern-Casus C₁ of C₂ ontvangen (dus, *A₁P₁, *A₂P₂, etc.).

De volgende acht condities worden verondersteld universeel te zijn en de afbeelding van inputs op outputs te beïnvloeden:

(19)	a	A → C1	:	A-argumenten ontvangen C1
	b	P → C2	:	P-argumenten ontvangen C2
	c	A ↛ C2	:	A-argumenten ontvangen geen C2
	d	P ↛ C1	:	P-argumenten ontvangen geen C1
	e	α ↛ C4	:	A- en P-argumenten ontvangen geen C4
	f	α → C2	:	Er is een argument dat C2 ontvangt
	g	X → C1	:	Hoog prominente argumenten ontvangen C1
	h	x ↛ C12	:	Laag prominente argumenten ontvangen geen C1 /C2

Met behulp van deze condities kan afgeleid worden dat normale transitieve zinnen met als input AP (een hoog prominente A en een hoog prominente P) altijd de output A₁P₂ opleveren, onafhankelijk van de rangschikking van de condities. Immers, alle mogelijke output kandidaten schenden conditie (g), maar alleen A₁P₂ voldoet aan alle andere condities. De output A₁P₂ moet dus wel de optimale output zijn voor alle mogelijke rangschikkingen van de condities.

Beschouw de intransitieve inputs A en P. Mogelijke outputs voor A zijn A₁, A₂ en A₄, voor P zijn dat P₁, P₂ en P₄. Aan de condities (a), (c) en (g) wordt voldaan door de output A₁; aan (f) wordt voldaan in het geval van A₂. Met andere woorden, (f) staat hoger in de hiërarchie dan (a), (c) en (g) in ergatieve talen, maar niet in nominatieve talen. Ga na dat de output A₄ nooit optimaal

[p. 122]

kan zijn. Voor P-inputs geldt dat P₂ de optimale output is, tenzij (g) hoger in de hiërarchie staat dan (b), (d) en (f). Dat laatste is blijkbaar het geval in nominatieve talen.

Laten we nu eens bekijken wat de optimale outputs zijn voor inputs met laag prominente A-argumenten (passiefconstructies) en die met laag prominente P-argumenten (antipassiefconstructies). De drie sterkste condities in de rangorde van nominatieve talen zijn volgens de hypothese (g) >> (h) >> (f) (waarbij >> staat voor strikt domineren). Zie de tabel in (20): (20a) laat zien wat de optimale output is voor intransitieven, (20b) voor passieven, en (20c) voor wat we antipassieven zouden kunnen noemen:

(20) Conditietabel voor nominatieve talen, bijvoorbeeld Nederlands
Input		Output	X→C1	x↛C12	α→C2
A	☞	A1			*
		A2	*
P	☞	P1			*
		P2	*
aP		a1P2	*	*
		a2P1		*
	☞	a4P1			*
		a4P2	*
Ap		A1p2		*
	☞	A1p4			*
		A2p4	*

Uit de tabel valt af te lezen dat aan het A-argument van een passiefconstructie C₄ wordt toegekend (inderdaad is het in het Nederlands zo dat de agens in een passief hetzij weggelaten wordt hetzij lexicale Casus krijgt van de prepositie door) terwijl het P-argument nominatieve Casus draagt:

(21)	Els1 wordt (door Petra4)4 geschaduwd

Voorbeelden van een ‘antipassiefconstructie’ in een nominatieve taal als het Nederlands zijn voorbeelden waarbij het P-argument weggelaten wordt of een oblique/lexicale Casus draagt (bijvoorbeeld uitgedeeld door een prepositie), en het A-argument nominatieve Casus draagt:

[p. 123]

(22)	Petra1 eet (van de appel4)4

In ergatieve talen is de rangorde van de drie sterkste condities net even anders: conditie (g) wordt nu gedomineerd door de andere twee, (h) en (f). In een tabel:

(23) Conditietabel voor ergatieve talen, bijvoorbeeld Inuit
Input		Output	x↛C12	α→C2	X→C1
A		A1		*
	☞	A2			*
P		P1		*
	☞	P2			*
aP		a1P2	*		*
		a2P1	*
		a4P1		*
	☞	a4P2			*
Ap		A1P2	*
		A1P4		*
	☞	A2P4			*

In ergatieve talen krijgt het laag prominente A-argument van passieven C₄ en het P-argument C₂; in antipassieven is het het laag prominente P-argument dat C₄ krijgt, terwijl het A-argument C₂ draagt. Het A-argument in een passiefconstructie draagt oblique Casus of wordt weggelaten (zie (24) uit het Labrador Inuit), terwijl ditzelfde geldt voor het P-argument in een antipassiefconstructie (zie (25a), Inuit, en (25b), Labrador Inuit):

(24)		Kivgak2 (kingminut4)4 kee-jau-vok
		De knecht wordt (door de honden) gebeten
(25)	a	Hansi2 inun-nik4 tuqut-si-vuq
		Hansi heeft mensen vermoord
	b	(Ujarqamik4)4 tigu-si -voq
		Hij nam (een steen)

[p. 124]

Een juiste rangschikking van slechts drie universele welgevormdheidscondities is dus al voldoende om de verschillen in Casusdistributie tussen nominatieve en ergatieve talen in intransitieven, passieven en antipassieven te verklaren. De andere condities worden in Legendre, Raymond en Smolensky (1993) aangewend om een derde type talen te beschrijven, het Lakhota-type talen met als optimale outputs A₁, P₂, a₁P₂, A₁p₄. Uit de condities kunnen ook universele implicaties worden afgeleid over de mogelijke combinaties van intransitieven, passieven en antipassieven die in een taal aangetroffen kunnen worden.

6 Conclusie

OT biedt een algemene methodologie om specifieke grammatica's af te leiden van universele welgevormdheidscondities. Cross-linguïstische variatie blijkt dan overeen te komen met de verzameling talen die op basis van universele condities tot de theoretische mogelijkheden behoren. Maar ook binnen één taal kunnen complexe patronen verklaard worden door de interactie van universele condities te bestuderen. Een voorbeeld van zo'n studie is Grimshaw (1995), waarin de distributie van hoofden in Engelse zinnen, inversie van subjecten en hulpwerkwoorden, en het voorkomen van do en that, verklaard worden met behulp van een handje vol conflictueuze condities in de juiste rangorde.

Een van de voordelen van zachte condities is dat ze algemeen en universeel geformuleerd kunnen worden. Harde condities moeten vaak aangepast worden om schendingen te kunnen verklaren: ze worden minder algemeen geformuleerd of er wordt aangenomen dat ze gered kunnen worden door lege categorieën of door aan te nemen dat ze in sommige gevallen pas op een later niveau van computatie (LF meestal) een rol gaan spelen.

In dit artikel heb ik vooral willen laten zien waar de succesvolle zachte condities vandaan komen. Ze komen niet uit de lucht vallen omdat taalkundige feiten er zo mooi mee verklaard kunnen worden, maar ze waren er al ruim voordat Smolensky eraan dacht zijn welgevormdheidstheorie (Smolensky 1986) te gaan toepassen op natuurlijke taal.^8.

8. Jack Hoeksema merkt op dat conflictueuze regels al vaker zijn voorgesteld in de taalkunde. Dat is zo, maar het aardige van de hier geschetste theorie is dat de conflictueuze aard van de condities volgt uit onafhankelijk onderbouwde connectionistische concepten en technieken.

[p. 125]

Bibliografie

Bobaljik, J.D. (1992) Nominally Absolutive is not Absolutely Nominative. Proceedings of WCCFL XI, CSLI, Stanford.

Bok-Bennema, R. (1991) Case and Agreement in Inuit, proefschrift Katholieke Universiteit Brabant.

Chomsky, N. (1992) A Minimalist Program for Linguistic Theory. MIT Occasional Papers in Linguistics #1. MITWPL, Cambridge, MA.

[p. 126]

Fodor, J.A., en Z.W. Pylyshyn (1988) Connectionism and Cognitive Architecture: A critical analysis. Cognition 28, 3-71.

Gelder, T. van (1990) Compositionality: A Connectionist Variation on a Classical Theme. Cognitive Science 14, 355-384.

Grimshaw, J. (1995) Projection, Heads, and Optimality. Ms. Rutgers University, New Brunswick NJ (te verschijnen in Linguistic Inquiry?).

Hebb, D.O. (1949), The Organization of Behavior. Wiley, New York.

Hoekstra, T. en R. Mulder (1990) Unergatives as Copular Verbs; Locational and Existential Predication. The Linguistic Review 7, 1-79.

Jordan, M.I. (1986) An Introduction to Linear Algebra in Parallel Distributed Processing. In D.E. Rumelhart, J. McClelland, and the PDP Research Group, Parallel Distributed Processing. Explorations in the Microstructure of Cognition. Volume 1: Foundations. MIT Press, Cambridge, MA.

Laka, I. (1993) Unergatives that Assign Ergative, Unaccusatives that Assign Accusative. In J.D. Bobaljik & C. Philips (eds.), Papers on Case & Agreement, MIT Working Papers in Linguistics 18, MITWPL Cambridge, MA.

Legendre, G. (1989) Unaccusativity in French. Lingua 79, 95-164.

Legendre, G., Y. Miyata en P. Smolensky (1990a) Harmonic Grammar - A formal multi-level connectionist theory of linguistic well-formedness: Theoretical foundations. Proceedings of the Twelfth Annual Meeting of the Cognitive Science Society, 388-395.

Legendre, G., Y. Miyata en P. Smolensky (1990b) Harmonic Grammar - A formal multi-level connectionist theory of linguistic well-formedness: An application. Proceedings of the Twelfth Annual Meeting of the Cognitive Science Society, 884-891.

Legendre, G., W. Raymond en P. Smolensky (1993) An Optimality-Theoretic Typology of Case and Grammatical Voice Systems. Proceedings of the 19th Meeting of the Berkeley Linguistics Society.

Rumelhart, D.E., G.E. Hinton, and J.L. McClelland (1986) A General Frame work for Parallel Distributed Processing. In D.E. Rumelhart, J. McClelland, and the PDP Research Group, Parallel Distributed Processing. Explorations in the Microstructure of Cognition. Volume 1: Foundations. MIT Press, Cambridge, MA.

Prince, A. en P. Smolensky (te verschijnen), Optimality Theory: Constraint Interaction in Generative Grammar. In Linguistic Inquiry Monograph Series. MIT Press, Cambridge, MA.

Smolensky, P. (1986) Information Processing in Dynamical Systems: Foundations of Harmony Theory. In D.E. Rumelhart, J. McClelland, and the PDP Research Group, Parallel Distributed Processing. Explorations in the Microstructure of Cognition. Volume 1: Foundations. MIT Press, Cambridge, MA.

Smolensky, P. (1991) Connectionism, Constituency, and the Language of Thought. In B. Loewer and G. Rey (eds.) Meaning in Mind. Fodor and his Critics. Basil Blackwell, Oxford, UK & Cambridge, MA.

Smolensky, P. (1995) Constituent Structure and Explanation in an Integrated Connectionist/Symbolic Cognitive Architecture. In C. Macdonald and G.

[p. 127]

Macdonald (eds.) Connectionism: Debates on Psychological Explanation, Basil Blackwell, Oxford, UK.

Zaenen, A. (1993) Unaccusativity in Dutch: Integrating Syntax and Lexical Semantics. In J. Pustejovski (ed.) Semantics and the Lexicon. Kluwer Academic Publishers, Dordrecht.