Tabu. Jaargang 21
(1991)– [tijdschrift] Tabu–
[pagina 175]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Monotonie en domeinselectie in statistische beweringen
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 176]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 Monotonie-eigenschappen van determinatorenIn eerste instantie gaan wij in dit artikel uit van de interpretatie van determinatoren zoals die is ontwikkeld in de theorie van Gegeneraliseerde Kwantoren. Determinatoren worden opgevat als uitdrukkingen die een relatie leggen tussen twee verzamelingen individuen, gegeven door respectievelijk het naamwoord dat samen met de determinator het subject vormt en het predikaat (maar cf. paragraaf 5 voor een andere visie). In (1a) bijvoorbeeld drukt alle de inclusierelatie uit tussen de verzameling kinderen en de verzameling zingende individuen. Deze relatie is expliciet gemaakt in (1b):
Zoals gebruikelijk in de modeltheoretische semantiek worden alle uitdrukkingen geïnterpreteerd met betrekking tot een bepaald model. We kunnen de semantiek van determinatoren dan algemeen opschrijven als volgt:
Dankzij de opvatting van determinatoren als relaties kunnen we de semantische eigenschappen van determinatoren onderzoeken met behulp van noties ontleend aan de theorie van relaties. Eén van de eigenschappen die in dit soort onderzoek een rol spelen betreft monotonie. We kunnen monotonie-eigenschappen in principe definiëren voor het linker- of het rechterargument. In dit artikel zullen we ons beperken tot monotonie in het rechterargumentGa naar eind2. . Een determinator is rechts monotoon stijgend wanneer hij voldoet aan het volgende criterium:
Met andere woorden, een determinator is rechts monotoon stijgend wanneer je inferenties kunt maken naar grotere verzamelingen. We zeggen van zulke kwantoren dat zij zijn gesloten onder supersets. Parallel hieraan kunnen we de eigenschap van dalende monotonie definiëren als in (4):
Rechts monotoon dalende kwantoren staan dus afleidingen toe naar kleinere verzamelingen: zij zijn gesloten onder deelverzamelingen. De monotonie-eigenschappen van determinatoren kunnen op eenvoudige wijze worden vastgesteld. We hebben eerder al gezegd dat we voorlopig aannemen dat het eerste argument van de kwantor het naamwoord is dat samen met de determi- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 177]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nator het subject vormt. Dit levert dus de verzameling A. De verzameling B correspondeert met de denotatie van het predikaat, dat het tweede argument van de kwantor vormt. Rechts monotonie kunnen we testen door de verzameling die correspondeert met het tweede argument van de kwantor te vergroten, respectievelijk te verkleinen. Stel dat de verzameling van individuen die luid zingen een deelverzameling is van de verzameling van individuen die zingen. Dan gelden voor monotoon stijgende en dalende kwantoren de volgende inferentiepatronen. De pijltjes drukken uit dat we uit de waarheid van de zin links van de pijl de waarheid van de zin rechts van de pijl kunnen afleiden:
Deze inferenties zijn bekend uit de literatuur over dit onderwerp (cf. Barwise and Cooper 1981, Zwarts 1986 e.a.), dus we hoeven hier niet lang bij stil te staan. We merken alleen op dat volgens deze standaardtest uidrukkingen als 80% van, de helft van, tweederde van, etc. rechts monotoon stijgend zijn, omdat zij gesloten zijn onder supersets. Er zijn echter ook voorbeelden die erop lijken te wijzen dat dergelijke uitdrukkingen helemaal niet monotoon stijgend zijn, maar eerder niet-monotoon, d.w.z. noch monotoon stijgend, nog monotoon dalend. Het gaat hier om constructies die veelvuldig voorkomen in statistische uitspraken. In dit artikel behandelen we twee typen van dit soort ongeldige inferentiepatronen. De twee constructies worden descriptief gelabeled als ‘veilig vrijen’ en ‘brieven met spelfouten’, naar aanleiding van de volgende voorbeelden. De doorgestreepte pijl drukt uit dat uit de waarheid van de eerste zin niet die van de tweede zin kan worden afgeleid, noch andersom:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 178]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Volgens de standaardanalyse verwachten we dat ongeldige afleidingen van dit type betekenen dat de determinator noch monotoon stijgend, noch monotoon dalend is. We zeggen dan kortweg dat de kwantor rechts niet-monotoon is. Maar dit is natuurlijk in tegenspraak met het gegeven dat proportionele determinatoren het gedrag vertonen van rechts monotoon stijgende kwantoren (zie (5c), (5d) en (5e)). De vraag die zich opdringt is of (7) en (8) werkelijke voorbeelden tegen het monotoon stijgende karakter van proportionele determinatoren zijn, of dat het slechts schijnbare tegenvoorbeelden betreft. Wij stellen ons op het standpunt dat het hier inderdaad slechts schijnbare tegenvoorbeelden betreft en zullen deze visie in de volgende paragrafen toelichten. De reden dat wij deze voorbeelden in verschillende secties behandelen is dat wij de mening zijn toegedaan dat er verschillende oorzaken ten grondslag liggen aan de ongeldigheid van de inferenties onder (7) en (8). Wij zullen eerst voorbeelden van het type ‘veilig vrijen’ nader onderzoeken en vervolgens de constructies van het type ‘brieven met spelfouten’ bespreken. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 ‘Veilig vrijen’De ongeldige inferentie onder (9a) lijkt een tegenvoorbeeld te vormen tegen het monotoon stijgende karakter van 80% van:
Het adverbium veilig lijkt een belangrijke rol te spelen in het niet doorgaan van de inferentie, gegeven de geldigheid van (7b), waarin het bijwoord veilig is vervangen door zijn tegenhanger onveilig. Als verklaring voor de ongeldigheid van (9a) kan worden aangevoerd dat niet-vrijen ook veilig vrijen is, zodat het heel goed mogelijk is dat een aanzienlijk deel van de Nederlandse jeugd veilig vrijt juist doordat zij niet vrijt. Voor onveilig vrijen geldt uiteraard niet zoiets: je kunt alleen onveilig vrijen door ook daadwerkelijk te vrijen, en dat op een onveilige manier te doen. Dit verklaart de geldigheid van de inferentie onder (9b). Het volgende Venn diagram laat één en ander duidelijk zien: 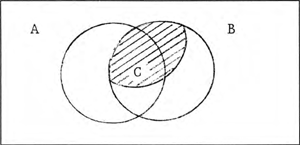 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 179]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In dit diagram geeft A de verzameling van de Nederlandse jeugd weer, B is de verzameling individuen die vrijen, C is de verzameling individuen die echt vrijen en wel op een veilige wijze. Het zal duidelijk zijn dat het complement van C onder B, d.w.z. B-C, nu de verzameling individuen omvat die vrijen op een onveilige wijze. De verzameling individuen die veilig vrijen omvat echter naast C ook alle individuen die niet vrijen, dus de hele verzameling E-B. De denotatie van veilig vrijen is in dit perspectief dus de verzameling C∪(E-B). Wanneer we nu de ongeldige inferenties onder (9a) en (9b) opschrijven in termen van verzamelingenleer ziet dat er als volgt uit:
Voor (10b) maakt dit onmiddellijk inzichtelijk waarom de inferentie geldig is: B-C is een deelverzameling van B, de determinator is monotoon stijgend, en dus gesloten onder supersets. Dit is voldoende om de conclusie in kwestie te mogen trekken. Voor (10a) is nu ook duidelijk dat C∪(E-B) géén deelverzameling is van B: individuen die lid zijn van deze verzameling hoeven expliciet niet de eigenschap B te hebben. Ondanks het monotoon stijgende karakter van de kwantor hoeft het dus geen verbazing te wekken dat de afleiding onder (10a) ongeldig is. Sterker nog: de ongeldigheid van (10a) heeft niets te maken met monotonie-eigenschappen! Merk op dat voorafgaand aan de monotonietests onder (5) en (6) expliciet wordt vermeld dat we aannemen dat de verzameling van individuen die luid zingen een deelverzameling is van de verzameling van individuen die zingen. Wanneer nu wordt gesteld dat de verzameling individuen die veilig vrijen helemaal geen deelverzameling is van de individuen die vrijen zijn we ver verwijderd van een adequate test voor monotonie-eigenschappen, omdat niet is voldaan aan de conditie dat er twee verzamelingen B en B' zijn die in een deelverzamelingsrelatie tot elkaar staan. We kunnen hieruit concluderen dat dergelijke contexten geen tegenvoorbeeld vormen voor de assumptie dat uitdrukkingen als 80% van rechts monotoon stijgend zijn. De lering die we hieruit moeten trekken is dat kennelijk niet alle adverbia de eigenschap hebben dat zij verzamelingen afbeelden op deelverzamelingen. Hiermee wordt het inferentiepatroon onder (9) een discussie over de lexicaal-semantische eigenschappen van het modificerende adverbium. Overigens is het verschijnsel dat hier wordt gesignaleerd tamelijk wijd verbreid. Een vergelijkbare situatie doet zich voor in (11), waarbij echter het ‘negatieve’ onvoldoende aanleiding geeft tot ongeldige inferenties, terwijl bij het ‘positieve’ voldoende in (11a) de inferentie wel doorgang vindt: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 180]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ook hier geldt weer dat ‘onvoldoende onderwijs’ ook kan betekenen ‘geen onderwijs’, wat aanleiding geeft tot een vergelijkbare situatie als onder (10) geschetst. Het contrast tussen veilig/onveilig enerzijds en voldoende/onvoldoende anderzijds maakt duidelijk dat we de specifieke lexicale kenmerken van dit type adverbia niet algemeen kunnen ophangen aan negatie: in sommige gevallen zal het ‘positieve’ adverbium het inferentiepatroon ongeldig maken, in andere gevallen zal dat gebeuren door zijn ‘negatieve’ tegenhanger. Kenmerkend voor alle voorbeelden is echter dat bij één van de adverbia de inferentie wel doorgang vindt. Dit ligt wel voor de hand: slechts één van beide adverbia zal het complement van de verzameling B erbij betrekken. Zijn tegenhanger zal dan, als een reguliere modificator, een deelverzameling van B selecteren. Hoewel we dus semantisch wel een mouw kunnen passen aan het probleem van de onverwacht ongeldige inferenties is het de vraag of we toch niet het type bewering zwaarder mee moeten laten wegen. De statistische uitspraken in onze voorbeeldzinnen zijn beweringen over een deel van een onderzochte populatie. Bij statistische uitspraken wordt meestal de onderzochte populatie -of een representatieve steekproef daaruit- tevoren nauwkeurig gedefinieerd. Het zou dan ook een beetje flauw zijn om te beweren dat onder de 80% van de Nederlandse jeugd die veilig vrijt ook dat deel van de jeugd valt dat helemaal niet (dus op de veiligst mogelijke wijze) de liefde bedrijft. De steekproef wordt namelijk zo samengesteld, dat alle leden van de groep de te onderzoeken eigenschap hebben. Doel van onderzoek is niet om de vraag te beantwoorden óf de Nederlandse jeugd vrijt, maar bedoeld wordt om na te gaan of er door de vrijenden overwegend veilig wordt gevrijd. Een laatste opmerking bij de voorbeelden onder (9) heeft betrekking op de voorkeur van deze zinnen voor een generische of habituele interpretatie. Dat wil zeggen: de zinnen doen uitspraken over de seksuele gewoontes van de Nederlandse jeugd, eerder dan over een incidentele handeling. We zullen zien dat dit een gemeenschappelijk kenmerk is van de ‘veilig vrijen’ voorbeelden en de constructies van het type ‘brieven met spelfouten’. Ook bij niet-generische interpretaties blijven de eerder gesignaleerde verschillen in inferentiepatroon echter bestaan:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 181]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Door de toevoeging van het bijwoord van tijd gisteravond wordt de mogelijkheid uitgesloten dat het hier om een beschrijving van de seksuele gewoontes van de Nederlandse jeugd gaat. Daarentegen wordt een concrete, eenmalige situatie beschreven. Aangezien de semantiek van veilig/onveilig dezelfde blijft geldt ook hiervoor nog steeds de situatie zoals die is geschetst onder (10) en verkrijgen we dezelfde inferentiepatronen. In de volgende paragraaf zal blijken dat dit een belangrijk verschil is met de ongeldige inferentiepatronen gelieerd aan ‘brieven met spelfouten’. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 ‘Brieven met spelfouten’In paragraaf 1 gaven we aan dat er naast het type ‘veilig vrijen’ nog andere constructies zijn waarin de inferenties die we vanuit het standaardmodel verwachten geen doorgang vinden. Als voorbeeld noemden we (8), hier herhaald als (13):
De ongeldigheid van de inferentie kan nu echter niet worden verklaard uit de semantiek van de adverbiale modificator, zoals voorgesteld voor de constructie van het type ‘veilig vrijen’. Hoewel niet-vrijen kan worden aangemerkt als een deelverzameling van veilig vrijen, kan het niet-schrijven van brieven uiteraard niet kan worden beschouwd als een deelverzameling van het schrijven van brieven met spelfouten.Ga naar eind4. Kennelijk is hier iets anders aan de hand. Opmerkelijk bij dit type monotonieproblemen is dat ze zijn gebonden aan een habituele interpretatie van de zin. De betekenis van (13) kan worden geparafraseerd als ‘Voor de helft van de schoolkinderen geldt dat als zij brieven schrijven, dit brieven met spelfouten zijn’. Deze parafrase maakt de intuïtie expliciet dat er een soort als..dan constructie, gelieerd aan een (impliciete) kwantificatie over gebeurtenissen, ten grondslag ligt aan de ongeldigheid van de inferentie in (13). Dat de habituele interpretatie verantwoordelijk is voor de ongeldigheid van de inferentie blijkt uit voorbeelden waarin een dergelijke gewoontelezing is geblokkeerd:
Door de toevoeging van het bijwoord van tijd gisteren wordt het onmogelijk een gewoontelezing te creëren, maar wordt een specifieke gebeurtenis beschreven zoals die op die dag plaats vond. De inferentie is nu niet langer ongeldig, want wanneer het een feit is dat minstens de helft van de schoolkinderen de eigenschap heeft dat zij gisteren brieven met spelfouten hebben geschreven, dan kan het niet anders of zij hebben gisteren brieven geschre- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 182]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ven.Ga naar eind5. Merk op dat deze observatie in scherp contrast staat met de interpretatie van (12). Dit wijst erop dat het type ‘veilig vrijen’ zich onderscheidt van het type ‘brieven met spelfouten’. Het contrast veilig/onveilig heeft te maken met de lexicaal-semantische eigenschappen van het adverbium, terwijl de ongeldigheid van (13) berust op de habituele interpretatie van de zin. Over de vraag waarom bepaalde zinnen een voorkeur hebben voor een habituele lezing en andere niet hebben zich reeds vele taalkundigen gebogen (vergelijk Dahl 1975, Schubert en Pelletier 1987, Carlson 1989 en anderen). In een definitief antwoord wordt door de literatuur niet voorzien. Voor een deel lijkt hier sprake te zijn van een pragmatische kwestie waarbij de centrale vraag is of het voor de hand ligt om bepaalde uitspraken als ‘regel’ of ‘generalisatie’ op te vatten. Gegeven het feit dat de twee typen constructies die in dit artikel worden besproken veelvuldig voorkomen in statistische uitspraken waarin het ‘algemene’ gedrag van de Nederlandse jeugd of van schoolkinderen onderwerp van discussie is wordt aan deze pragmatische eis duidelijk voldaan. Hoewel we dus niet altijd precies kunnen aangeven waar de habituele interpretatie van zinnen als (13) vandaan komt hebben we doorgaans vrij goede intuïties over het voorkomen van dergelijke lezingen. De vraag die hieruit voortvloeit is dan hoe we deze habituele interpretatie precies representeren en op welke manier we monotonie-eigenschappen in habituele zinnen uitwerken. Aan deze kwestie is de volgende paragraaf gewijd. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 Monotonie in habituele zinnenIn de literatuur merkt men op dat generische en habituele interpretaties veelal een relationele structuur vereisen. Dat vinden we terug in de als..dan-constructies die corresponderen met een (impliciete) kwantificatie over gebeurtenissen: ‘als ze vrijen, vrijen ze veilig’, ‘als ze brieven schrijven, schrijven ze brieven met spelfouten’. Naast deze relationele habituele interpretaties lijken er inherent habituele eigenschappen te zijn zoals roken, drinken, zwemmen en mogelijk ook vrijen en schrijven. Met deze inherent habituele eigenschappen corresponderen duidelijk geen als..dan constructies. Wanneer iemand de slechte gewoonte heeft om te roken, dan betekent dat niets anders dan dat de persoon in kwestie met zekere regelmaat een rokertje opsteekt (cf. bijvoorbeeld Kleiber 1987 en De Swart 1987 voor discussie over het onderscheid tussen relationele en niet-relationele gewoontes). Om de impliciete kwantificatie over gebeurtenissen die kenmerkend is voor habituele zinnen expliciet te maken kunnen we een beroep doen op generieke operatoren of kwantoren, zoals die in de literatuur zijn ingevoerd (cf. Carlson 1978, Gerstner en Krifka 1989 en anderen). Voor zinnen als (15a) gebruiken we een tweeplaatsige kwantor GEN2, die leidt tot een relationele interpretatie: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 183]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De kwantor GEN2 drukt een relatie uit tussen de verzameling gebeurtenissen waarin Anneke brieven schrijft en de verzameling gebeurtenissen waarin Anneke brieven met fouten schrijft. Wanneer we GEN2 lezen als ‘gewoonlijk’ of ‘meestal’Ga naar eind6. betekent dit dat een gebeurtenis waarin Anneke brieven schrijft er bijna altijd zo uitziet dat zij brieven met fouten schrijft. (15c) formuleert de waarheidscondities zo dat het aantal gevallen waarin Anneke brieven zonder fouten schrijft kleiner is dan één of ander contextafhankelijk getal m. Dit correspondeert in grote lijnen met de betekenis die wij aan een zin als (15a) toekennen. Inherent habituele predikaten, waarvoor geen relationele interpretatie geldt, kunnen worden weergegeven met een eenplaatsige generieke operator GEN1:
In plaats van een relatie te leggen tussen twee verzamelingen gebeurtenissen drukt GEN1 uit dat Marieke de gewoonte heeft om te drinken. Een dergelijke uitspraak heeft in onze samenleving doorgaans betrekking op de gewoonte alcohol te drinken, en zo zullen we deze zin dan ook opvatten. Hoeveel en hoe vaak Marieke moet drinken om haar deze complexe eigenschap toe te kunnen kennen blijft vaag. Het wordt niet precies vastgelegd door de operator GEN1 en in veel gevallen is het afhankelijk van context en situatie. Om die reden voeren we in (16c) een norm n in die deze contextafhankelijkheid opneemt in de waarheidscondities van de zin: de zin is waar wanneer de frequentie waarmee Marieke drinkt hoog genoeg is om van een gewoonte te kunnen spreken. Het zal duidelijk zijn dat er meer te zeggen valt over de representatie van habituele eigenschappen, maar we hebben genoeg aan (15b) en (16b) om de monotonie-eigenschappen van habituele zinnen te kunnen bestuderenGa naar eind7.. Neem aan dat de zinnen onder (17) telkens een habituele interpretatie krijgen. Op grond van de volgende inferentiepatronen kunnen we stellen dat zowel de GEN1 als de GEN2-operator monotoon stijgend is:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 184]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De gewoonte te roken en te drinken kan worden beschouwd als een meer beperkte eigenschap dan de gewoonte te roken. De inferentie onder (17a) wijst erop dat GEN1 is gesloten onder extensie. Op dezelfde manier kunnen we stellen dat het schrijven van brieven met spelfouten en grammaticale fouten mag worden beschouwd als een deelverzameling van het schrijven van brieven met spelfouten. Ook GEN2 is dus gesloten onder supersets. Merk op dat hoewel zowel GEN1 als GEN2 in dit verband worden beschouwd als monotoon stijgende kwantoren, we niet automatisch de inferentie kunnen maken van GEN1 naar GEN2 of andersom. Met andere woorden, (18) is ongeldig in beide richtingen:
Immers, wanneer Marieke doorgaans wijn drinkt als ze (alcohol) drinkt volgt daar nog niet uit dat zij voldoende vaak en veel drinkt om haar de gewoonte toe te kennen dat zij drinkt. Met andere woorden, het kan zijn dat er vrijwel geen situaties zijn waarin Marieke wel (alcohol) drinkt maar iets anders dan wijn, terwijl de frequentie waarmee zij drinkt toch niet voldoet aan de conditie onder (16c). In zijn algemeenheid kunnen we dus niet zomaar overstappen van GEN1 naar GEN2 of andersom. In de zinnen onder (16)-(18) staan telkens eigennamen in subjectpositie. Aangezien dit artikel echter gaat over monotonie-eigenschappen van proportionele determinatoren als 80% van, de helft van, etc. gaan we nu over tot het bestuderen van voorbeelden met gekwantificeerde NPs in subjectpositie. In plaats van gewoontes van specifieke personen beschouwen we in dergelijke zinnen de gewoontes van de helft van de Nederlandse jeugd of van 80% dan wel tweederde van de studenten:
De geldige en ongeldige inferentiepatronen onder (19) kunnen nu eenvoudig worden verklaard met behulp van de monotonie-eigenschappen van habituele zinnen, zoals die zijn toegelicht aan de hand van (16)-(18). In (19a) is sprake van een relationele gewoonte, die we kunnen beschrijven met behulp van GEN2 (cf. 15). Aangezien GEN2 monotoon stijgend is geldt voor elk individu dat de gewoonte heeft brieven met spelfouten en stijlfouten te schrijven dat dit individu de gewoonte heeft brieven met spelfouten te schrijven. Hieruit kunnen we eenvoudig afleiden dat de verzameling individuen die de gewoonte hebben brieven met spelfouten en stijlfouten te schrijven een deelverzameling | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 185]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
is van de verzameling individuen die de gewoonte hebben brieven met spelfouten te schrijven:
De twee verzamelingen B en B' die in (19a) corresponderen met de denotatie van het predikaat voor en na de pijl staan dus in een deelverzamelingsrelatie tot elkaar. Dit maakt (19a) een geschikte context om monotonie-eigenschappen van de determinator in te testen. Het feit dat inferentie naar een grotere verzameling is toegestaan bevestigt het karakter van 80% van als een rechts monotoon stijgende kwantor. Eenzelfde redenering verklaart de geldige inferentie onder (19b). Ook daar geldt dat de gewoontes in een inclusierelatie tot elkaar staan, zoals we in (17) hebben gezien. We mogen hieruit afleiden dat de verzameling individuen die de gewoonte heeft te roken en te drinken een deelverzameling is van de verzameling individuen die de gewoonte heeft te drinken. Ook in (19b) staan dus de denotaties van het predikaat voor en na de pijl in een inclusierelatie tot elkaar, en bevestigt het doorgang vinden van de inferentie het monotoon stijgende karakter van de determinator. Het ongeldige inferentiepatroon in (19c) is nauw verwant aan dat in (18). Uit de uitspraak dat een bepaald individu gewoonlijk wijn drinkt mogen we niet afleiden dat dit individu de gewoonte heeft te drinken. Hieruit volgt onmiddellijk dat de verzameling individuen die gewoonlijk wijn drinken geen deelverzameling is van de verzameling individuen die de gewoonte hebben te drinken. Aangezien we alleen van een adequate monotonietest kunnen spreken wanneer de denotaties van het predikaat voor en na de pijl in een inclusierelatie tot elkaar staan kunnen we uit (19c) niet concluderen dat proportionele determinatoren niet-monotoon zijn. Het zal inmiddels duidelijk zijn dat het type voorbeeld dat we descriptief hebben gelabeled als ‘brieven met fouten’ van het type van (19c) is. De overgang van het habituele ‘brieven met fouten schrijven’ naar het eveneens habituele ‘brieven schrijven’ kan worden opgevat als een overgang van een GEN2 naar een GEN1 kwantor. In zijn algemeenheid dient dat te worden beschouwd als een ongeldige inferentie. De verzamelingen van individuen die die gewoontes hebben staan dan ook niet in een deelverzamelingsrelatie tot elkaar, zodat de ongeldigheid van (13) slechts een schijnvoorbeeld is tegen het monotoon stijgende karakter van de helft van. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 DomeinselectieEen complicerende factor voor de analyse van statistische beweringen is dat het eerste en het tweede argument van de kwantor niet altijd overeenkomen met respectievelijk het naamwoord en de VP, zoals we hebben aangenomen in sectie 1. Vergelijk (21a) (= 5c) en (21b): | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 186]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In sectie 1 hebben we betoogd dat volgens de standaardopvatting over gegeneraliseerde kwantoren in (21a) het eerste argument van de kwantor wordt gegeven door het naamwoord, en in dit geval dus bestaat uit de hele populatie van kinderen. De betekenis is dan:
oftewel, de intersectie van de verzameling kinderen en de verzameling luid zingenden bevat 80% van de kinderen. Het is echter de vraag of dit juist is. Eén van de moeilijkheden bij het interpreteren van statistische uitspraken is, dat (21a) ambigu is tussen de interpretaties (22) en (23):
(23) is de betekenis van (21b). In (23) is het eerste argument van de kwantor samengesteld uit het naamwoord en een deel van het predikaat. Merk op dat de betekenissen van (22) en (23) verschillend zijn: uit (23) volgt niet dat 80% van de kinderen zong. De interpretatie in (23) is dus duidelijk anders dan wat de standaardopvattingen over kwantificatie voorspellen. De ambiguïteit van (21a) als gerepresenteerd in (22) en (23) wijst erop dat we soms ons domein van kwantificatie anders moeten kiezen dan de standaardanalyse suggereert. Het is een voor de hand liggende gedachte om de argumentstructuur van de kwantor in (21a) te analyseren op dezelfde manier als die van focusadverbia (vgl. Rooth 1985). Bezie de volgende voorbeelden (hoofdletters duiden op sterk intonationeel accent):
(24a) en (24b) hebben verschillende waarheidscondities. Een eenvoudige semantiek voor de zinnen onder (24) wordt gegeven in (26):
Laten we de rechterargumenten van de supersetrelatie het domein noemen, en de linkerargumenten de denotatie. Het focusaccent in (24a) en (24b) bepaalt niet alleen het linkerargument, maar ook het rechter. Men kan zich voorstellen dat er een procedure in de syntaxis is die het gefocusseerde element in de zin vervangt door een variabele van het juiste type. Rooth | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 187]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(1985) heeft een iets andere analyse voorgesteld. Om hier niet ter zake doende redenen neemt hij aan dat slechts een VP modificator is. De superset relatie die slechts uitdrukt is er dan niet één tussen verzamelingen individuen, maar tussen verzamelingen eigenschappen. Het resultaat voor (24a) is dan dat de verzameling met als enige lid de eigenschap Marie aan Suze voorstellen een superset is van de verzameling eigenschappen van Jan van de vorm iemand aan Suze voorstellen. Voor (24b) wordt dat, dat de verzameling met als enige lid de eigenschap Marie aan Suze voorstellen een superset is van de verzameling eigenschappen van Jan van de vorm Marie aan iemand voorstellen. Het aardige is dat de denotatie, het linker lid van de superset relatie, in alle gevallen gelijk is. Het enige wat verandert is het domein. Iets dergelijks kan worden gedaan voor (25). Hoewel de kwantor 80% van gewoon verzamelingen individuen als argumenten neemt, kunnen we ook hier de denotatie constant houden, en alleen het domein met de wisselende intonatie doen veranderen. (28a) en (28b) zijn de betekenissen van respectievelijk (25a) en (25b), met parafrases (27a) en (27b):
Wat we nu kunnen zien is dat hoewel de kwantor 80% van wel degelijk een rechts monotoon stijgende kwantor is, in (28a) het resultaat 80% van de kinderen zingt niet bereikt kan worden: laten we het rechter lid groeien tot alle zingende kinderen, dan blijft er over dat 80% procent van de zingende kinderen een zingend kind is. En hoewel dat waar is, zegt het niets over het percentage zingende kinderen ten opzichte van de verzameling kinderen. Merk overigens op dat we in het algemeen uit de vaststelling dat 80% van de X Y zijn, niet kunnen concluderen dat 20% van de X niet-Y zijn. Dat deze conclusie op pragmatische gronden getrokken wordt, mag blijken uit het voorbeeld van iemand die wedt dat hij 80% van de kegels om zal gooien en ze vervolgens allemaal omkegelt. Uiteraard mogen we dan zeggen dat hij zijn weddenschap wint. Opnieuw geldt dat het statistische karakter van de beweringen in niet geringe mate bijdraagt tot de keuze van het domein waarover wordt gekwantificeerd. We hebben boven al vermeld dat het gebruikelijk is om een steekproef zo samen te stellen dat alle leden van de groep de te onderzoeken eigenschap hebben. Doel van onderzoek is niet het beantwoorden van de vraag of de Nederlandse jeugd vrijt, en of de kinderen in kwestie zingen respectievelijk brieven schrijven. Bedoeld wordt na te gaan of er door de vrijenden overwegend veilig wordt gevrijd, door de zingenden vooral luid wordt gezongen en door de brieven schrijvenden meestal foutloos wordt geschreven. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 188]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Men kan zich nu nog afvragen waarom (21a) ambigu is, aangezien hard niet gefocusseerd is. Focus is echter een sterk aan de pragmatiek gelieerd fenomeen, wat mag blijken uit de volgende voorbeeldenGa naar eind8.:
(29a) en (29b) hebben dezelfde waarheidscondities, maar andere gebruikscondities. Dit mag blijken uit het feit dat (29a) een antwoord kan zijn op de vraag ‘Wie houdt er van Marie?’ en (29b) op de vraag ‘Van wie houdt Jan?’, maar niet vice versa. (29c) is een lastiger geval. Hoewel het lijkt dat houden van de enige tweeplaatsige relatie is die er tussen Jan en Marie bestaat, kan dit niet juist zijn. Als Jan van Marie houdt, is het ook zo dat Jan van Marie houdt of de pest aan haar heeft. Wat (29c) uitdrukt kan niet op dezelfde wijze geanalyseerd worden als de zinnen in (24). (29d) beweert dat Jan niet van Marie houdt, en suggereert dat Jan van iemand anders houdt. Die suggestie is geen logisch gevolg (zie: ‘Jan houdt niet van MARIE, sterker nog, hij houdt van niemand!’). Op dezelfde wijze suggereert (29e) dat Jan wel van andere meisjes houdt. Die suggestie wordt gewekt doordat de spreker, als deze had willen uitdrukken dat Jan helemaal niet van meisjes hield de modificator met krulletjes weg had kunnen laten: volgens het eerste Griceaanse maxime van kwantiteit kan de luisteraar van (29e) concluderen dat de sterkere bewering ‘Jan houdt niet van meisjes’ niet waar is volgens de spreker. Dit Griceaanse principe heeft tot gevolg dat modificatoren per default een focusinterpretatie krijgen: als er geen ander afwijkend focusaccent is, of enige andere aanwijzing van het tegendeel, mag worden aangenomen dat de modificator in focus staat (vgl. Gabbay and Moravcsik 1978). (21a) krijgt nu dus per default de interpretatie (28a). Maar het blijft een pragmatische default regel, waarvan makkelijk afgeweken kan worden. Dit verklaart de ambiguïteit. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6 ConclusieIn dit artikel hebben we de monotonie-eigenschappen van proportionele determinatoren als 80% van, de helft van, tweederde van onder de loep genomen. We hebben gezien dat zij volgens de standaardtest rechts monotoon stijgend zijn. In veel statistische uitspraken ontstaan echter schijnbare tegenvoorbeelden tegen deze claim, omdat bepaalde inferenties ongeldig blijken te zijn. Wij betogen dat dit in alle gevallen te maken heeft met de argumentstructuur van de zinnen in kwestie. Een context is alleen een adequate test voor rechts monotonie wanneer de denotaties van het predikaat voor en na de pijl in een inclusierelatie tot elkaar staan. Zowel in de voorbeelden van het type ‘veilig vrijen’ als in de habituele lezingen van zinnen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 189]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
van het type ‘brieven met spelfouten schrijven’ wordt niet aan deze conditie voldaan. Het niet doorgaan van de inferentie in dergelijke contexten heeft dan ook niet te maken met de monotonie-eigenschappen van de kwantoren in kwestie. Tenslotte hebben wij een paragraaf gewijd aan constructies waarin de argumentstructuur niet in overeenstemming is met de standaardopvattingen. Wij betogen dat domeinselectie cruciaal is in een adekwate interpretatie van statistische beweringen. Op grond van deze observaties concluderen wij dat er vooralsnog geen steekhoudende argumenten zijn om proportionele determinatoren in statistische beweringen niet-monotoon te verklaren. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 190]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Referenties
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

