Logo DBNL
Tabu. Jaargang 20 (1990)

Tabu. Jaargang 20

(1990)– [tijdschrift] Tabu–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

Een procedure voor redeneren met kwantoren
Edith Kaan, Mark Kas en Rick Ruhland

0 Inleiding*

In Kas en Hoekstra (1989) en Hoekstra en Kas (1990) wordt het LISP-programma De Behulpzame Bibliothecaris (verder aan te duiden als BB) beschreven. Dit programma kan vragen met daarin gekwantificeerde uitdrukkingen beantwoorden. De vragen moeten betrekking hebben op de stand van zaken in een bepaald domein, in dit geval een bibliotheek. Het programma kan overweg met een vraag als ‘Zijn alle boeken aanwezig?’, waarin alle boeken de gekwantificeerde uitdrukking is. Maar ook de kwantoren geen N, een N, de n N, minstens n N, hoogstens n N, de meeste N, enkele N, beide N en n N kunnen door BB verwerkt worden.

Om tot een antwoord te komen kan het programma van twee strategieën gebruikmaken, namelijk zoeken plus tellen en redeneren. In de volgende paragraaf zal in grote lijnen worden uiteengezet hoe deze strategieën in de oorspronkelijke versie van BB worden toegepast. Zoals echter al in Kas en Hoekstra (1989) is vastgesteld, kende deze versie van BB de nodige beperkingen. Ook deze beperkingen zullen in paragraaf 1 ter sprake komen.

Vervolgens zullen we in paragraaf 2 voorstellen doen om de redeneercomponent van BB te verbeteren. Door deze verbeteringen wordt het mogelijk om meer kwantoren te gebruiken bij het afleiden van nieuwe uit oude antwoorden. Dit levert een praktisch voordeel op, omdat BB hierdoor beter gaat redeneren en dus meestal1 sneller een antwoord zal geven. In theoretisch opzicht zijn de verbeteringen interessant, omdat ze ons meer inzicht verschaffen in de relaties tussen verschillende kwantoren.

We sluiten dit artikel af met enkele conclusies, problemen en vingerwijzingen voor nader onderzoek.

1 Korte beschrijving van BB

1.1 De principes van BB

Het doel van het maken van BB was te onderzoeken of en hoe de theorie der gegeneraliseerde kwantoren (GK, zie e.g. Barwise and Cooper (1981), Van Benthem (1986), Zwarts (1981, 1983, 1986)) was om te zetten in computerprogrammatuur. Het idee hierachter was dat de theorie der GK het juiste kader zou kunnen verschaffen om een computer gekwantificeerde uitdrukkingen te laten verwerken. Indien die onderstelling juist zou blijken te zijn, dan zou daarmee het onderzoek naar de constructie van zogenoemde Natuurlijke-Taal-Interfaces (NTI's) een stapje in de goede richting hebben gezet. Immers, een

volwaardige NTI zou ook gekwantificeerde uitdrukkingen moeten kunnen verwerken. En het waren nu juist die gekwantificeerde uitdrukkingen die in het verleden voor de nodige problemen zorgden in natuurlijke taal verwerkende systemen. Zo gebruikten bijvoorbeeld Warren and Pereira (1982) een soort predikaatlogica om gekwantificeerde uitdrukkingen te representeren. Hierdoor kregen de kwantoren a, some en the[singular] alle drie dezelfde representatie, namelijk het predikaat exists (overeenkomend met de existentiële kwantor uit de predikaatlogica). De theorie der GK ontleent nu juist haar bestaansrecht aan het feit, dat een dergelijke representatie te grof is en onvoldoende recht doet aan de semantische verschillen tussen de kwantoren die in natuurlijke taal voorkomen.

In BB worden de natuurlijke taal kwantoren dan ook niet omgezet in een of andere (predikaatlogische) representatie, maar worden zij simpelweg gerepresenteerd in natuurlijke taal. Een kwantor als alle wordt bijvoorbeeld gerepresenteerd als ALLE, enkele als ENKELE, enz. De semantiek van deze kwantoren wordt bepaald door hun semantische definitie. Alvorens we de semantische definities kunnen presenteren, moeten we eerst even ingaan op het zoeken en tellen van BB.

2.2 Zoeken en tellen

Zoals in de inleiding al is vermeld, werkt BB op een bepaald domein. Dat domein bestaat uit een klein gedeelte van de bibliotheek van de Groningse Letterenfaculteit. Deze bibliotheek bestaat uit een cluster van een groot aantal afdelingsbibliotheken. In BB bestaat de Letterenbibliotheek uit de bibliotheken van de vakgroepen Nederlands, Engels en Frans. In totaal zijn er 25 boeken door deze bibliotheken aangeschaft. De aangeschafte boeken kunnen zich in één van de volgende vier toestanden bevinden: aanwezig, uitgeleend, bij-binder en gejat. Er wordt in BB dus een onderscheid gemaakt tussen aangeschaft en aanwezig: aangeschaft is de default-waarde voor ieder boek in de bibliotheek (ieder boek is ooit aangeschaft), aanwezig wil zeggen dat het boek daadwerkelijk op de plank staat.

Het boekenbestand wordt door BB in een bepaalde structuur opgeborgen (zie voor een gedetailleerde beschrijving Kas en Hoekstra (1989)). Wanneer nu een gebruiker een vraag stelt aan BB, dan wordt uit zijn vraag een rijtje met relevante gegevens gedestilleerd. Zo'n rijtje heet in het programma een catlijst (‘categorieënlijst’). De abstracte structuur van een catlijst is als in (1), waarin tc staat voor taalcode, d.i. de code die de bibliotheek van een bepaalde vakgroep heeft. Zo hebben boeken in de bibliotheek van Nederlands de code 32, die van Frans de code 22 en die van Engels de code 36. rc staat voor rubriekscode, d.i. de code die iedere rubriek heeft. Zo heeft de rubriek syntaxis de code 19 en de rubriek semantiek de code 20. naam staat voor de achternaam van de auteur en titel voor de titel van het boek.

(1) (<tc> <rc> <naam> <titel>)

Als de gebruiker één of meer van deze gegevens niet in zijn vraag vermeldt, wordt in de catlijst op de daarmee corresponderende plaatsen een vraagteken geplaatst. Zie (2) en (3).

(2) a Zijn alle boeken van Chomsky over syntaxis met als titel ‘Aspects of the Theory of Syntax’ bij Nederlands aanwezig?
  b = > catlijst = (32 19 (CHOMSKY) ‘Aspects of the Theory of Syntax’)
 
(3) a Zijn er enkele boeken over semantiek van Wierzbicka uitgeleend?
  b = > catlijst = (? 20 (WIERZBICKA)?)

Nadat de gebruiker een vraag als (3a) heeft ingetypt, gaat BB twee dingen doen. Allereerst wordt het aantal boeken geteld dat zich in de gevraagde toestand bevindt. Na (3a) worden bijvoorbeeld alle uitgeleende boeken over semantiek van Wierzbicka geteld. Het getal dat dit telwerk oplevert wordt in BB aangeduid als ait (= ‘aantal in toestand’). Vervolgens gaat het programma ook alle aangeschafte boeken van Wierzbicka over semantiek tellen. Dit laatste getal gaat in BB door het leven als aib (= ‘aantal in bestand’).

We zijn nu voldoende toegerust om de semantische definities te bespreken. De vraag in de theorie der GK is altijd: aan welke voorwaarden moet de stand van zaken in het domein voldoen, wil een uitspraak over dat domein waar zijn? Vertaald naar BB is de vraag: wat moet de stand van zaken in de bibliotheek zijn om een gestelde vraag met ja te beantwoorden? Voor vraag (2a) met de gekwantificeerde uitdrukking alle boeken kunnen we deze voorwaarde definiëren als in (4).

(4) aib = ait

Immers, wanneer het aantal aanwezige boeken van Chomsky enz. precies gelijk is aan het aantal ooit aangeschafte boeken van Chomsky enz., dan is het zo dat alle boeken van Chomsky enz. aanwezig zijn. Als (4) waar is, kan BB dus ja antwoorden op de gestelde vraag. Geldt (4) niet, dan zal BB nee antwoorden.2

Op deze wijze zijn voor alle kwantoren in BB de waarheidscondities gedefinieerd. Ze zijn hieronder in (5) samengebracht. Voor de volledigheid zijn de overeenkomstige semantische definities uit Zwarts (1986a) in de derde kolom geplaatst. In (5) staat N voor nomen en n voor een willekeurig getal > = 0.3

(5)

Kwantor BB definitie Zwarts (1986a)
Geen N ait = 0 {X c U: Kard (∥N∥U ∩ X) = 0}
Een N ait ≥ 1 geen definitie
De n N aib = ait = getal {X c U: Kard (∥N∥U - X) = 0} en Kard (∥N∥U ∩ X) = n}
Het N aib = ait = 1 geen definitie
Enkele N ait ≥ 2 {X c U: Kard (∥N∥U ∩ X) ≥ 2}
Beide N aib = ait = 2 {X c U: Kard (∥N∥U - X) = 0} en Kard (∥N∥U ∩ X) = 2}
Minstens n N ait ≥ getal {X c U: Kard (∥N∥U ∩ X) ≤ n}
Hoogstens n N ait ≤ getal {X c U: Kard (∥N∥U ∩ X) ≥ n}
De meeste N (0.5* aib) < ait {X c U: Kard (∥N∥U - X) > Kard (∥N∥U ∩ X)
Alle N aib = ait {X c U: Kard (∥N∥U - X) = 0}
n N ait ≥ getal {X c U: Kard (∥N∥U ∩ X) = n}4

1.3 Redeneren

In het bovenstaande hebben we laten zien hoe BB door middel van zoeken en tellen een antwoord op een vraag kan vinden. Maar BB kan nog meer! Wanneer een vraag door middel van zoeken en tellen is beantwoord, wordt de vraag met het gegeven antwoord in de vorm van een item opgeslagen op het zogenoemde blackboard. Het blackboard is als het ware het geheugen van het programma. Een blackboard-item ziet er in abstracto als volgt uit:

(6) (<catlijst> <kwantor> <toestand> <antwoord> <aib> <ait> <getal>)

Het blackboard-item van vraag (3a) ziet eruit als in (7).

(7) ((? 20 (WIERZBICKA)?) ENKELE UITGELEEND NEE 20?)

Omdat ait 0 was en de semantische definitie van enkele zegt dat ait > = 2 voor een bevestigend antwoord, heeft BB nee geantwoord op vraag (3a). Al deze gegevens zijn op het blackboard terug te vinden. Verder bevat het

blackboard-item de catlijst, de toestand (in dit geval uitgeleend), de waarde van aib (in dit geval 2; er zijn dus in totaal twee boeken uitgeleend, maar blijkens de waarde van ait zijn die boeken niet van Wierzbicka) en de waarde van getal (in dit geval?. Getal krijgt een waarde indien een samengestelde kwantor als minstens 3 wordt gebruikt).

Stel dat de gebruiker nu (8) zou vragen.

(8) Zijn alle boeken van Wierzbicka over semantiek uitgeleend?

Het antwoord op deze vraag is af te leiden uit het antwoord op vraag (3a). Als we immers hebben vastgesteld dat het niet zo is, dat er enkele boeken van Wierzbicka over semantiek zijn uitgeleend, dan is het ook niet zo dat alle boeken van Wierzbicka over semantiek zijn uitgeleend. Uit het antwoord nee op (3a) kunnen we het antwoord op (8) afleiden: dat moet ook nee zijn. Dit verband tussen de twee vragen, de kwantoren en de antwoorden is weergegeven in regel (9). Hierin is Q1 de kwantor in de eerstgestelde vraag (=(3a)), Ant1 het antwoord op die vraag, Q2 de kwantor in de tweede vraag (= (8)) en Ant2 het afgeleide antwoord.

(9) ALS Q1=enkele & Ant1=nee & Q2=alle DAN Ant2=nee

In (3a)-(8) was sprake van een gelijkblijvend vraaggebied.5 Het ging immers in beide vragen over de boeken van Wierzbicka over semantiek. Indien (3a) gevolgd zou zijn door vraag (10) zouden we te maken hebben gehad met een kleiner wordend vraaggebied, en indien (3a) gevolgd zou zijn door (11) met een groter wordend vraaggebied.

(10) Zijn er minstens 3 boeken van Wierzbicka over semantiek met als titel ‘The Semantics of Grammar’ uitgeleend?
(11) Is er een boek van Wierzbicka uitgeleend?

Vraag (10) is namelijk specifieker dan vraag (3a), terwijl vraag (11) juist betrekking heeft op een grotere verzameling boeken dan vraag (3a).

Voor kleiner en groter wordende vraaggebieden gelden weer andere afleidingsregels dan voor gelijkblijvende vraaggebieden. Het voert in het bestek van dit artikel echter te ver om daar dieper op in te gaan.6

De conclusie is dus dat er antwoorden kunnen worden afgeleid uit eens gestelde vragen en gegeven antwoorden. We moeten ons echter wel bedenken dat dit niet altijd zo hoeft te zijn. Bezie het volgende geval.

(12) a Is er bij Engels een boek van Chomsky aanwezig?
  b JA ER ZIJN ZELFS 3 BOEKEN BIJ ENGELS VAN CHOMSKY AANWEZIG
(13)   Zijn alle boeken van Chomsky bij Engels aanwezig?

Op (12a) heeft BB ja geantwoord. Dit wil zoveel zeggen als: er is inderdaad minstens 1 boek van Chomsky bij Engels aanwezig (zie de semantische definitie van een in (5)). Uit dit gegeven kunnen kunnen we evenwel geen antwoord op (13) afleiden. We weten immers alleen dat er minstens 1 boek aanwezig is, maar niet of ook alle andere ooit aangeschafte boeken op de planken staan. Uit (12a) + (12b) is dus geen antwoord op (13) af te leiden. Er zit voor BB niets anders op dan het antwoord op (13) te vinden door middel van zoeken en tellen.

De afleidingsregels van BB zijn alle gerepresenteerd als in (9). Deze wijze van representeren is weliswaar heel helder en zorgt voor een snel werkend programma, maar levert toch ook problemen op. Deze zullen worden besproken in de volgende paragraaf.

1.4 Beperkingen van BB

Hoewel het bovenstaande wellicht de indruk wekt dat BB een perfecte interface vormt tussen een bibliotheekbezoeker en het bibliotheekbestand, is dit zeker niet het geval. De in Kas en Hoekstra (1989) en Hoekstra en Kas (1990) beschreven versie van BB kent een aantal serieuze beperkingen. Om er een paar te noemen: BB bevat geen goede ontleedcomponent (parser). Het programma kan daardoor maar met een bepaald type zinnen overweg. Ook voor de representatie van het boekenbestand en het doorzoeken daarvan is geen gebruik gemaakt van de slimme technieken die hiervoor in de afgelopen jaren ontwikkeld zijn. Dit betekent dat het programma veel te traag is om met een serieus boekenbestand overweg te kunnen. Een derde beperking is de manier waarop de afleidingen worden gemaakt. Deze beperking is het onderwerp van de rest van dit artikel.

Het maken van afleidingen vindt in BB plaats aan de hand van redeneerschema's die bestaan uit regels zoals (9). Dergelijke redeneerschema's zijn declaratief. Dat wil zeggen: ze geven een opsomming van alle mogelijke combinaties. Wie die opsommingen beziet, wordt al snel door de gedachte bevangen dat er een of ander systeem ten grondslag moet liggen. Wij vroegen ons af: Waarom kunnen sommige afleidingen wel en andere niet worden gemaakt? Een antwoord op deze vraag is in theoretisch opzicht interessant, omdat het ons iets zegt over de wijze waarop de verschillende kwantoren zich tot elkaar verhouden. De opsommingen als zodanig zeggen ons daarover uiteraard niets.

Het grote voordeel van uitvoerige opsommingen is, dat ze het programma makkelijker maken. We kunnen grofweg stellen: hoe langer de opsommingen, hoe eenvoudiger het programma dat met die opsommingen moet werken. Behalve de omstandigheid dat ze ons niets wijzer maken over de verhoudingen tussen de kwantoren, is er nog een ander nadeel. In een declaratieve representatie kunnen kwantoren als minstens n N, hoogstens n N, de n N, n N, enz. nooit worden opgenomen. Het aantal waarden van n is immers on-

beperkt en dus niet op te nemen in een opsomming.

Kwantoren als minstens n N nopen de programmeur ertoe de declaratieve benadering in te ruilen voor een procedurele. Procedures bestaan uit reeksen instructies. Dit in tegenstelling tot de declaratieve redeneerschema's, die uitsluitend uit reeksen gegevens bestaan. Door nu in het programma de procedures op te nemen die de afleidingen beregelen, slaan wij twee vliegen in één klap. Op de eerste plaats kunnen nu ook kwantoren als minstens N in de afleidingen worden betrokken en ten tweede kan het aantal kwantoren waarmee BB overweg kan, moeiteloos worden uitgebreid. Het enige dat nodig is, is dat de nieuwe kwantor met zijn definitie in het lexicon van BB wordt opgenomen. De procedure zorgt er vervolgens voor dat de kwantor bij het maken van afleidingen wordt betrokken. Deze voordelen wegen ruimschoots op tegen het nadeel dat het programma ingewikkelder wordt en dat niet meer in één oogopslag te zien is welk antwoord er zal worden afgeleid.

In de volgende paragraaf zullen we de procedure uit de doeken doen die het redeneerschema voor gelijkblijvende vraaggebieden moet vervangen.

2 Een procedurele representatie van BB's redeneercomponent

2.1 Inleiding

Bij het zoeken naar een procedurele representatie van de redeneercomponent zijn we van de volgende gedachte uitgegaan. Een vraag met een kwantor (Q1) creëert te zamen met het antwoord op die vraag (Ant1) een soort zoekruimte. Om uit Q1 + Ant1 nu een antwoord op een tweede vraag met een kwantor (Q2) af te kunnen leiden, moet Q2 in die zoekruimte ‘passen’. Het gaat er dus om een procedure te ontwerpen die de zoekruimte gecreëerd door Q1 + Ant1 definieert en die kan beslissen of Q2 al dan niet in deze ruimte past. Deze procedure zal worden gegoten in de vorm van een algoritme, weergegeven in een stroomschema. Het stroomschema is opgenomen in de bijlage. De theoretische basis ervan zal in paragraaf 2.2 en 2.3 worden gelegd. In paragraaf 2.4 zullen we een aantal voorbeelden van de werking van de procedure laten zien.

2.2 Zewit- en zenit-gebieden

Welke zoekruimte creëert Q1 + Ant1? Stel dat de vraag ‘Zijn alle boeken aanwezig?’ bevestigend is beantwoord. Q1 is dus alle en Ant1 is ja. We weten dan zeker dat elk aantal boeken aanwezig is dat groter of gelijk is aan 2 en kleiner of gelijk is aan aib, dat wil zeggen: twee boeken zijn aanwezig, drie boeken zijn aanwezig, ...., aib boeken zijn aanwezig. Voor Q1=alle + Ant1= ja geldt dus: 2 = < zoekruimte = < aib. We noemen deze zoekruimte een zewit-gebied. Zewit staat voor zeker wel in toestand. In (14a) is het zewit-

gebied van alle + ja in beeld gebracht.

Is Q1 een en Ant1 ja, dan weten we zeker dat er één boek aanwezig is. Er kunnen best meer boeken aanwezig zijn, maar daar kan niets met zekerheid over gezegd worden. Q1=een + Ant1=ja creëert dus ook een zewitgebied, namelijk 1 = < zoekruimte = < 1, oftewel: zoekruimte = 1. Zie (14b).

Een geheel andere situatie ontstaat wanneer Q1 enkele is en Ant1 nee. We weten dan zeker dat elk aantal boeken dat groter of gelijk is aan 2 niet aanwezig is. Q1 = enkele + Ant1 = nee creëert dus een soort negatieve zoekruimte. Deze zoekruimte noemen we een zenit-gebied (zenit = zeker niet in toestand). Zie (14c).

(14) /// = zeker wel aanwezig = zewit-gebied
  \\\ = zeker niet aanwezig = zenit-gebied
  niet-gearceerd = onbekend



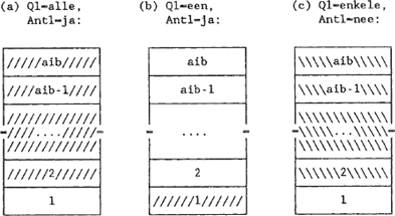illustratie

Op deze wijze kan voor elk van de kwantoren uit (5) worden nagegaan wat hun zewit- en zenit-gebied is. In (15) en (16) zijn alle gegevens samengebracht. Zr staat voor zoekruimte.

(15)

Q1 Ant1 zenit
geen N nee 1 ≤ zr ≤ 1
een N ja 1 ≤ zr ≤ 1
de n N ja 1 ≤ zr ≤ n & aib=n
het N ja 1 ≤ zr ≤ 1 & aib=1
enkele N ja 1 ≤ zr ≤ 2
beide N ja 1 ≤ zr ≤ 2 & aib=2
minstens n N ja 1 ≤ zr ≤ n
hoogstens n N nee 1 ≤ zr ≤ n+1
de meeste N ja 1 ≤ zr ≤ 0.5*aib+1
alle N ja 2 ≤ zr ≤ aib
n N ja 1 ≤ zr ≤ n

(16)

Q1 Ant1 zenit
geen N ja aib ≥ zr ≥ 1
een N nee aib ≥ zr ≥ 1
de n N nee aib ≥ zr ≥ n & aib=n
het N nee aib ≥ zr ≥ 1 & aib=1
enkele N nee aib ≥ zr ≥ 2
beide N nee aib ≥ zr ≥ 2 & aib=2
minstens n N nee aib ≥ zr ≥ n
hoogstens n N ja aib ≥ zr ≥ n+1
de meeste N nee aib ≥ zr ≥ 0.5* aib+1
alle N nee aib ≥ zr ≥ aib
n N nee aib ≥ zr ≥ n

Aan de hand van (15) en (16) kunnen verschillende observaties worden gedaan. De eerste is, dat het rechtergetal in de formules bij alle kwantoren in zowel hun zewit- als hun zenit-gebied hetzelfde is. We zullen dit getal het z-getal noemen.

Het tweede dat opvalt is dat geen N en hoogstens n N zich afwijkend gedragen ten opzichte van de andere kwantoren. Beide kwantoren creëren, in tegenstelling tot de andere kwantoren, een zewit-gebied bij een nee-antwoord en een zenit-gebied bij een ja-antwoord. Erg verbazend is dit overigens niet. Immers, geen N en hoogstens n N zijn monotoon dalende kwantoren, terwijl alle andere monotoon stijgend zijn.

Verder kunnen we nog constateren dat sommige kwantoren een extra voorwaarde bij zich hebben. Dit blijken precies de zogenoemde presuppositionele kwantoren te zijn: de n N, het N en beide N. Deze kwantoren eisen dat het vraaggebied in kwestie een bepaald aantal elementen bevat. Wanneer aan deze voorwaarde niet is voldaan, kan de kwantor niet geïnterpreteerd worden.7

Voordat er nu geredeneerd kan worden, moeten we ook nog vaststellen op welke wijze Q2 in de zewit- en zenit-gebieden gecreëerd door Q1 + Ant1 moet passen. We kunnen daar kort over zijn. Een Q2 krijgt hetzelfde z-getal als een Q1. Er is dus geen verschil tussen het z-getal van enkele als Q1 of als Q2. Om nu een antwoord te kunnen afleiden moet het z-getal van Q2 binnen het zewit- of zenit-gebied gecreëerd door Q1 liggen. Een voorbeeld zal duidelijk maken hoe dit in zijn werk gaat.

Stel dat de vraag ‘Zijn alle boeken aanwezig?’ met ja is beantwoord, en dat aib = 10. Dan is er dus het volgende zewit-gebied gecreëerd: 1 = < zr = < 10. Wanneer vervolgens de vraag ‘Zijn er enkele boeken aanwezig?’ wordt gesteld, wordt er gekeken of het z-getal van enkele ( = 2) past binnen het gecreëerde zewit-gebied, dus 1 = < 2 = < 10. Dit is inderdaad het geval en dus kan de vraag ‘Zijn er enkele boeken aanwezig?’ met ja worden beantwoord.

In dit voorbeeld creëerden Q1 + Ant1 een zewit-gebied. Er kan echter ook een zenit-gebied ontstaan, bijvoorbeeld wanneer de vraag ‘Zijn alle boeken aanwezig?’ met nee zou zijn beantwoord. In een dergelijk geval moet

gekeken worden of het z-getal van Q2 groter of gelijk is aan dat van Q1. Als dat het geval is, dan luidt het antwoord op de tweede vraag nee (met uitzondering van geen N en hoogstens n N).

2.3 Twee basiskwantoren: minstens n en hoogstens n

2.3.1 Monotone stijgers: type M en type PK

We hebben hierboven gezien dat het verschil in de verhouding tussen zewiten zenit-gebieden precies correspondeert met een verschil in monotonieeigenschappen van de kwantoren. De kwantoren laten zich dus op natuurlijke wijze in twee groepen onderverdelen. Binnen de groep van de monotone stijgers moeten we nog de subklasse van presuppositionele kwantoren onderscheiden. Deze subklasse zullen we aanduiden als kwantoren van het type PK.

De zewit- en zenitgebieden van de monotone stijgers hebben alle de volgende structuur:

(17) a zewit: 1 = < zr = < n
  b zenit: aib > = zr > = n

Dit is evenwel precies de definitie van minstens n N. Dat klopt ook, want alle monotone stijgers kunnen ‘omgeschreven’ worden naar een formule met minstens:

(18) een = minstens 1
  de n = minstens n & aib = n
  het = minstens n & aib = 1
  enkele = minstens 2
  beide = minstens 2 & aib=2
  de meeste = minstens 0.5*aib+1
  alle = minstens aib
  n = minstens n

Van dit gegeven zullen we in de redeneerprocedure gebruikmaken. De kwantoren in (18) die niet van het type PK zijn, zullen we aanduiden als kwantoren van het type M (‘minstens’).

2.3.2 Monotone dalers: type H

Van de monotoon dalende kwantoren is iets minder makkelijk in te zien hoe ze gekarakteriseerd moeten worden. Een voorbeeld kan helpen dat inzicht te laten ontstaan.

Stel dat iemand vraag (19a) heeft gesteld en dat BB daarop met (19b) heeft geantwoord.

(19) a Zijn er minstens 3 boeken aanwezig?
  b JA ER ZIJN MINSTENS 3 BOEKEN AANWEZIG

We weten nu zeker dat er in ieder geval 3 boeken aanwezig zijn. De situatie is precies tegenovergesteld wanneer vraag en antwoord zouden zijn zoals in (20).

(20) a Zijn er hoogstens 3 boeken aanwezig?
  b JA ER ZIJN HOOGSTENS 3 BOEKEN AANWEZIG

We weten nu namelijk niet of er één, twee of drie boeken aanwezig zijn. Het enige dat we zeker weten is dat het vierde (vijfde, enz.) boek niet aanwezig is. Het zenit-gebied van hoogstens begint dus pas bij vier, dat wil zeggen drie + één. Dit vinden we dan ook terug in de zenit-formule voor hoogstens n N: aib > = zr > = n+1.

Een soortgelijke redenering kan worden gehouden met betrekking tot geen N. Als is bevestigd dat er geen boeken aanwezig zijn, dan weten we zeker dat boek-1, boek-2, enz. niet aanwezig zijn. Ook geen N begint dus als het ware te tellen bij n+1, waarbij voor geen geldt dat n=0. Geen N kan dus als een variant van hoogstens N worden opgevat, namelijk als hoogstens 0 N.

We zullen hoogstens n N en geen N kwantoren van het type H noemen. Hun algemene zewit- en zenit-formule is:

(21) a zewit: 1 = < zr = < n + 1
  b zenit: aib >= zr > = n + 1

2.4 De procedure in actie

In 2.2 en 2.3 hebben we de theoretische basis gelegd voor de procedure die afleidingen moet kunnen maken bij gelijkblijvende vraaggebieden. In de bijlage is het stroomschema van de procedure opgenomen. In deze paragraaf zullen we enkele voorbeelden behandelen om een idee te geven van de werking van de procedure.

Het eerste voorbeeld is te vinden in (22). Hierin is (a) de eerste vraag die door de gebruiker is gesteld, (b) het antwoord dat daarop is gegeven nadat BB gezocht en geteld heeft, (c) het item dat op het blackboard is gezet na de beantwoording van de vraag, (d) de tweede vraag van de gebruiker en (e) het antwoord dat BB heeft afgeleid met behulp van de gegevens van het blackboard-item.

Voorbeeld 1.

(22) a Zijn er geen boeken over syntaxis bij Frans aanwezig?
  b INDERDAAD ER ZIJN GEEN BOEKEN OVER SYNTAXIS BIJ FRANS AANWEZIG
  c ((22 19??) GEEN AANWEZIG JA 0 0?)
  d Is er een boek over syntaxis aanwezig?8
  e NEE HOOR

In het boekenbestand van de vakgroep Frans zijn geen boeken over syntaxis opgenomen. We zien dit terug in het blackboard-item (waarvan in (23) de structuur voor het gemak nog een keer wordt herhaald), dat vermeldt dat aib en ait beide 0 waren.

(23) (<catlijst> <kwantor> <toestand> <antwoord> <aib> <ait> <getal>)

De procedure begint bij start (blok 1). Via de vraag of Q2 (= de tweede kwantor = een) van het type PK is (blok 6) en de vraag of Q1 (= eerste kwantor = geen) van het type M of PK is (blok 12), komen we bij de vraag of Q1 van het type H is (blok 17). Dat is het geval. Daarom gaan we vanuit blok 17 we naar blok 18. Daar wordt gevraagd of het antwoord dat op het blackboard staat nee is. Dat is niet het geval. En dus gaan we vanuit blok 18 naar blok 14. Daar stellen we vast dat Q2 van het type M is. Dit gegeven voert ons naar blok 8. Daar wordt gevraagd of de ait groter is dan zQ2, hetgeen staat voor ‘het z-getal van de tweede kwantor’. Ait is 0 en het z-getal van een is 1. 0 is niet groter dan 1 en daarom gaan we naar blok 9, waar wordt gevraagd of ait=zQ2. Omdat dit niet zo is, kunnen we ook dat blok meteen via de nee-lijn verlaten. In blok 10 wordt gevraagd of het z-getal van een groter is dan dat van geen. Dat is niet het geval, want het z-getal is van beide 1. De vraag of zQ2=zQ2 in blok 11 kan dan ook met ja worden beantwoord, waarna het programma ervoor zorgt dat de woorden NEE HOOR op het scherm verschijnen.

 

Voorbeeld 2.

(24) a Zijn er minstens 9 boeken bij Nederlands aanwezig?
  b JA ER ZIJN MINSTENS 9 BOEKEN BIJ NEDERLANDS AANWEZIG
  c ((32???) MINSTENS AANWEZIG JA 13 9 9)
  d Zijn er minstens 8 boeken aanwezig?
  e JAZEKER
  f Zijn er hoogstens 8 boeken aanwezig?
  g INTEGENDEEL
  h Zijn er hoogstens 9 boeken aanwezig?
  i INDERDAAD

Dit voorbeeld heeft betrekking op de situatie die in paragraaf 2.3.2 is behandeld. We zien dat het antwoord op vraag (24a) is verkregen door zoeken en tellen. Uit het blackboard-item kunnen we opmaken, dat er bij Nederlands dertien boeken zijn (aib = 13) en dat er daarvan negen aanwezig zijn (ait=9). Welnu, als er minstens 9 boeken aanwezig zijn, dan zijn er ook minstens 8 boeken aanwezig. De procedure zorgt (blijkens (24e)) voor het juiste antwoord. Beslissend voor dit antwoord is blok 8, het blok waar wordt gevraagd of ait > zQ2. In dit geval dus of 9 > 8. Dit is inderdaad zo en daarom wordt JAZEKER als antwoord gegeven.

Dat op vraag (24f) geheel in overeenstemming met wat we zouden verwachten INTEGENDEEL wordt geantwoord, komt doordat de procedure een andere route neemt dan bij de beantwoording van (24d). Hoogstens 8 is immers een kwantor van het type H. Na blok 14 (type Q2 = H?) gehad te hebben, gaat de procedure verder met de vraag in blok 15: ait < zQ2? Met andere woorden: precies het tegenovergestelde van de vraag die bij minstens 8 werd gesteld. Het z-getal van hoogstens 8 is 9, namelijk 8 + 1 (zie (21a)). Omdat 9 niet kleiner is dan 9 gaat de procedure naar blok 21 en levert INTEGENDEEL als antwoord af.

Het is nu eenvoudig in te zien waarom (24h) met INDERDAAD wordt beantwoord. Het beslissende blok is weer 15: ait < zQ2? En dat is zo, want 9 < 6 (=9+1).

 

Voorbeeld 3.

(25) a Zijn er enkele boeken van Heim?
  b NEE
  c ((32 ? (HEIM) ?) ENKELE AANGESCHAFT NEE 11?)
  d Is er een boek van Heim?
  e JAZEKER

De procedure kan meer afleidingen maken dan strikt logisch gezien mogelijk is. Vraag (25a) is, na zoeken en tellen, ontkennend beantwoord. Hieruit kunnen we afleiden dat er één boek of geen boeken van Heim door de bibliotheek zijn aangeschaft, maar we weten niet welke van deze twee situaties het geval is. Van een vraag als (25d) zou het antwoord dan ook eigenlijk via zoeken en tellen gevonden moeten worden. De door ons ontworpen procedure heeft echter zoveel gegevens tot haar beschikking, dat toch een antwoord kan worden afgeleid. Beslissend is de vraag in blok 24: ait = zQ2? We weten dat ait = 1 (zie het blackboard-item) en ook dat het z-getal van een 1 is. Het antwoord op de vraag is dus ja en de verbaasde gebruiker ziet JAZEKER op het scherm verschijnen.

3 Conclusie

Wij hebben in dit artikel laten zien dat een procedure kan worden ontworpen die antwoorden afleidt uit vragen met daarin gekwantificeerde uitdrukkingen. Het blijkt dus mogelijk te zijn de declaratieve redeneercomponent van BB althans ten dele om te zetten in een procedurele. We hebben daarbij dankbaar gebruikgemaakt van inzichten afkomstig uit de theorie der gegeneraliseerde kwantoren.

De procedure heeft als nadeel dat de overzichtelijkheid van de redeneerschema's verloren gaat. Het grote (en ook doorslaggevende) voordeel is evenwel, dat met één en dezelfde procedure een veel groter aantal kwantoren kan worden betrokken bij het maken van afleidingen. De uitbreiding van de redeneercomponent met andere kwantoren is nu een fluitje van een cent geworden. In BB hoeven slechts de semantische definitie en het z-getal van de kwantor te worden opgenomen om de kwantor volledig te betrekken bij het spel der afleidingen. In een declaratieve benadering zou zo'n uitbreiding veel meer voeten in de aarde hebben, omdat voor iedere kwantor afzonderlijk zou moeten worden vastgesteld of een afleiding mogelijk is. In de procedurele benadering hoeven we ons daarover echter niet druk te maken, omdat de procedure generaliseert over de eigenschappen van de kwantoren.

Hoewel dit resultaat tot tevredenheid stemt, zijn er voldoende redenen om nog niet rustig achterover te gaan zitten. Er zijn nog (minstens) drie belangrijke kwesties die om behandeling vragen. De eerste is de behandeling van kwantoren die noch monotoon stijgend noch monotoon dalend zijn (de zogenoemde continue kwantoren (zie Zwarts (1986a)). De tweede is de integratie van de groter en kleiner wordende vraaggebieden in de procedure. De derde heeft betrekking op een kwestie die in dit artikel niet ter sprake is gekomen, namelijk het verband tussen kwantoren, de predikaten aanwezig, uitgeleend, etc. en de antwoorden. Het is immers duidelijk dat een positief antwoord op de vraag ‘Zijn alle boeken uitgeleend?’ een negatief antwoord op de vraag ‘Is er een boek aanwezig?’ impliceert. Pas wanneer deze kwesties zijn opgelost, zullen we de beschikking hebben over een complete redeneercomponent. De drie kwesties behoeven evenwel nog grondige doordenking. Wij hopen er bij een latere gelegenheid op terug te komen.

Bibliografie

Barwise, J., and R. Cooper (1981). ‘Generalized Quantifiers and Natural Language’, in: Linguistics and Philosophy 4: 159-219.
Van Benthem, J. (1986). Essays in Logical Semantics, Dordrecht.
Hoekstra, E., en M. Kas (1990). ‘The Interpretation of Natural Language Quantifiers: A System for Reasoning with Natural Language’ in: Literary and Linguistic Computing 5, nr. 2 (te verschijnen).
De Jong, F., en H.J. Verkuyl (1985). ‘Generalized Quantifiers: the Properness of their Strength’, in: J. van Benthem en A. ter Meulen (eds.) Generalized Quantifiers in Natural Language (GRASS 4), Dordrecht: 21-43.
Kas, M., en E. Hoekstra (1989). De Behulpzame Bibliothecaris. Een LISP-programma voor het interpreteren van en het redeneren met gekwantificeerde uitdrukkingen. Verslag vakgroep alfa-informatica, Groningen.
Warren, D.H., and F.C.N Pereira (1982). ‘An Efficient Easily Adaptable System for Interpreting Natural Language Queries’, in: American Journal of Computational Linguistics 8: 110-119.
Zwarts, F. (1981). ‘Negatief Polaire Uitdrukkingen I’, in: GLOT 4: 35-132.
Zwarts, F. (1983). ‘Determiners: a relational perspective’, in: A. ter Meulen (ed.) Studies in Modeltheoretic Semantics (GRASS 1), Dordrecht: 37-62.
Zwarts, F. (1986a). Categoriale grammatica en algebraïsche semantiek, proefschrift RU Groningen.
Zwarts, F. (1986b). ‘Polariteit: de reikwijdte van een lexicale eigenschap’, in: C. Hoppenbrouwers e.a. (eds.), Syntaxis en lexicon, Dordrecht: 157-192.

Bijlage: Het stroomschema van de procedure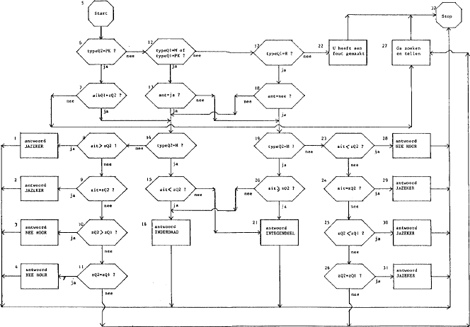



illustratie


Vorige Volgende

Over dit hoofdstuk/artikel

auteurs


taalkunde