Tabu. Jaargang 14

[p. 1]

[Nummer 1]

Een kategoriale beschrijving van het Nederlands
Joop Houtman

0. Inleiding

Dit artikel bevat een voorstel voor een kategoriale beregeling van een groot aantal lastige verschijnselen in de Nederlandse syntaxis. Het bouwt voort op recent werk van Steedman (cf. Steedman 1983), maar probeert een groter terrein te bestrijken, althans wat de beschrijving van het Nederlands aangaat.

Met Steedman (cf. ook Ades & Steedman 1982) maak ik gebruik van een nondirektioneel kategoriaal systeem, d.w.z. een systeem waarin de onderlinge volgorde van een funktor en zijn argument in principe vrij is. (Voor een nuttige inleiding tot de kategoriale grammatika, cf. het overzicht in Levelt 1973: 91-102.) Tot het hulpvocabulaire van het systeem behoren naast de primitieve (d.w.z. niet-samengestelde) kategorieën, waartoe het speciale symbool S (voor: zin) behoort, ook alle symbolen van de vorm X/Y, waar X en Y zelf ook kategorieën zijn. Een element van de kategorie X/Y vormt, in kombinatie met een element van de kategorie Y een groep van de kategorie X. In zo'n groep is het element van de kategorie Y het argument en het element van de kategorie X/Y de funktor.

Het belang van een dergelijke onderverdeling in funktoren en argumenten blijkt vooral in de semantiek, waar de semantische typen in het ideale geval een preciese weerspiegeling zijn van de syntaktische kategorieën. (cf. Montague 1973). In dit artikel wordt op het semantische aspekt echter niet verder ingegaan.

De voornaamste vraag in dit artikel is stellig hoe, gegeven een plausibele toewijzing van kategorieën aan de lexicale elementen, de kombinatieregels geformuleerd moeten worden om de grammatikale woordvolgorde te krijgen in Nederlandse hoofd- en bijzinnen, waarbij traditioneel problematische verschijnselen als de verbale verstrengeling in de eindgroep niet uit de weg worden gegaan. Daarbij zal blijken, dat het gebruik van een nondirektioneel systeem voor het Nederlands vruchten afwerpt, omdat vaak meerdere volgorden van funktor en argument mogelijk zijn (voor verwante analyses van het Engels, zie Flynn 1981,

[p. 2]

Ades & Steedman 1982). Bijvoorbeeld:

(1)	Wie eet appels?	(hoofdzin)
(2)	wie appels eet	(bijzin)

Met Hoeksema 1980 maak ik een onderscheid tussen VP₀ (finiete VP), VP₁ (infiniete VP zonder te - een zgn. ‘kale’ infinitief-groep), VP₂ (infiniete VP met te) en VP₃ (voltooid deelwoord-groep). Werkwoorden zijn al die lexicale elementen die reduceerbaar zijn tot een VP-kategorie. Reduceerbaarheid kunnen we aldus definiëren:

RED.:	(i)	X is reduceerbaar tot X
	(ii)	X/Y is reduceerbaar tot X
a	(iii)	Als X reduceerbaar is tot Y, en Y tot Z, dan ook X tot Z.

Volgens deze definitie is dus de reduceerbaarheidsdefinitie reflexief en transitief. Enkele voorbeelden: (VP₁/NP/NP is reduceerbaar tot VP₁, en dus een werkwoord, maar S/VP₂ is geen werkwoord, omdat het niet reduceerbaar is tot VP₂.

In dit artikel wordt, in navolging van Ades & Steedman (1982), de afkorting X$ gebruikt voor iedere kategorie die reduceerbaar is tot X.

Voor het subjekt wordt de kategorie S[-H]/VP₀ gepostuleerd, waarbij het kenmerk [-H] aangeeft, dat de betreffende S een bijzin is. In hoofdzinnen is de kategorie van de persoonsvorm van de vorm S$/(S[-H]/VP₀), die reduceerbaar is tot S, de kategorie van hoofdzinnen, terwijl de overeenkomstige kategorie in bijzinnen de vorm S[-H]$ heeft. Deze dubbele kategorisering van de persoonsvorm is ingevoerd en beargumenteerd in Steedman (1982: 28-29). Het komt er op neer dat de verschillen in woordvolgorde in hoofd- en bijzinnen wordt opgehangen aan een verschil in kategorisering van het finiete werkwoord in deze twee omgevingen. Het effekt van de kategorietoewijzing is, dat in hoofdzinnen de persoonsvorm een groep vormt met het subjekt, zodat een VP konstituent niet opgebouwd kan worden. Als evidentie voor het afwezig zijn van een groepsverband tussen de persoonsvorm en de erop volgende objekten in hoofdzinnen en het aanwezig zijn van zo'n verband tussen de persoonsvorm en de eraan voorafgaande objekten in

[p. 3]

de bijzin voert Steedman het kontrast in nevenschikkingsmogelijkheden in de volgende zinnen aan:

(3)	a	*Jan of wint of verliest.
	b	Ik denk dat Jan of wint of verliest.
(4)	a	*Jan en snoeit de rozen en plant de tulpen.
	b	.., dat Jan en de rozen snoeit en de tulpen plant.

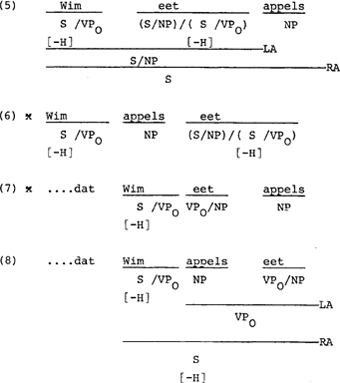
Verder is het effekt van de dubbele kategorisering, dat in hoofdzinnen de persoonsvorm de hoofdfunktor is en in bijzinnen het subjekt. Ter illustratie volgen nu de afleidingen van enkele hoofd- en bijzinnen.

[p. 4]

Door de zo dadelijk te geven kondities op applikatie is het mogelijk de zinnen (6) en (7) uit te sluiten zonder daarmee de acceptabele zinnen (5) en (8) te verwerpen. Kortheidshalve korten we in hoofdzinnen de kategorie S[-H]/VP_O af tot NP_s als in (9).

In hoofdstuk 1 komt applikatie aan de orde. Er worden kondities geformuleerd waaraan voldaan moet zijn voordat de applikatieregels werken. Hoofdstuk 2 gaat over funktie-kompositie, een mechanisme dat aangesproken moet worden als de funktor en zijn bijbehorende argument niet naast elkaar staan. In hoofdstuk 3 wordt ingegaan op verschijnselen, die in de transformationele taalkunde bekend staan onder de termen Extrapositie en V-raising. Tevens worden de verschijnselen Accusativus cum Infinitivo en Infinitivus pro Participio aan de orde gesteld. Tenslotte wordt in hoofdstuk 3 een voorstel gedaan voor een metaregel, die nodig is om zinnen met V-klusters af te leiden.

1. Applikatie

Applikatie is, zoals we in de inleiding gezien hebben, konkatenatie van twee woorden of woordgroepen, waarbij de noemer van de funktorkategorie gelijk is aan de kategorie van het argument. De kategorie van de gehele woordgroep is gelijk aan de teller van de funktorkategorie.

Applikatie ie een mechanisme dat ingeperkt moet worden, omdat er funktoren zijn die hun argument altijd links of altijd rechts zoeken. In 1.1 komt rechts-applikatie aan de orde, in 1.2 links-applikatie.

[p. 5]

1.1. Rechts-applikatie

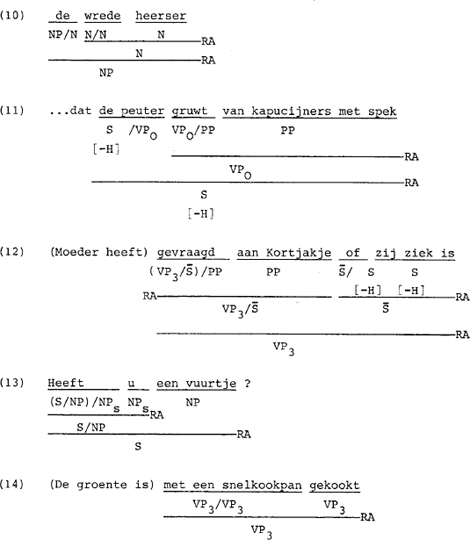
We spreken van rechts-applikatie als het argument rechts van de funktor staat. Zoals onderstaande gegevens laten zien, hoeft er aan deze regel maar één beperking gesteld te worden.

[p. 6]

De zinnen (10) t/m (17) laten zien dat rechts-applikatie mogelijk is, behalve als tegelijkertijd geldt dat de teller van de funktor gelijk is aan VP (ga dit na voor VP₁ en VP₂) en het argument een NP is.

De regel voor rechts-applikatie luidt aldus:

RA X/Y Y → X, tenzij X=VP en Y=NP

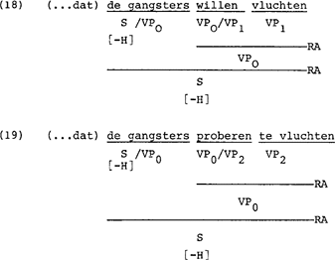
Een probleem duikt op als we voorbeelden met willen en proberen met elkaar vergelijken.

[p. 7]

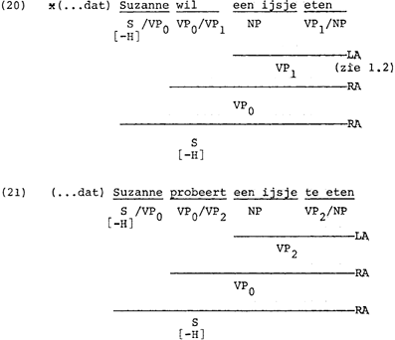
Zoals zin (18) laat zien, kunnen we niet de rechts-applikatie VP₀/VP₁ VP₁ → VP₀ uitsluiten om de ongrammatikaliteit van (20) te verklaren. In 1.2 zal blijken dat ook NP VP₁/NP → VP₁ niet gemist kan worden. Om zin (20) uit te filteren moeten we een feature toevoegen aan de kategorie van willen. Ik stel voor het feature [+L] als volgt in te voeren: willen → VP₀/VP₁[+L]. [+L] betekent in dit geval dat het argument van willen in het lexikon moet staan.

Vluchten in (18) voldoet aan die eis, een ijsje eten in (20) niet. De klasse van werkwoorden die het feature [+L] verlangen van hun argument is precies de klasse van Verb-raising werkwoorden, ook wel hulpwerkwoorden genaamd. Zoals nog zal blijken is een transformationele regel van werkwoordsverheffing onnodig in het onderhavige kader.

In de kategorie voor willen als persoonsvorm in de hoofdzin moet het feature juist niet aanwezig zijn, gezien de grammatikaliteit van (22). Willen moet hier ook niet gespecificeerd worden voor [-L]: (S/VP₁ [-L])/NP_s, omdat ook (23) een grammatikale zin is.

[p. 8]

1.2. Links-applikatie

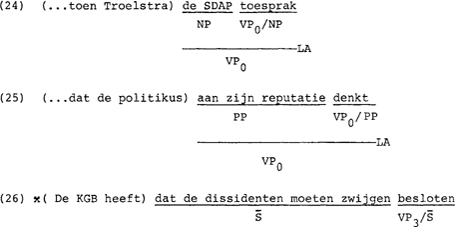
Bij links-applikatie staat het argument links van de funktor. Het is van toepassing op komplementen bij de VP, behalve op S̄-komplementen. We zien dit in (24) t/m (27).

[p. 9]

Links-applikatie komt ook voor bij een groep funktoren van de vorm S$, zoals te zien is in (28) t/m (30).

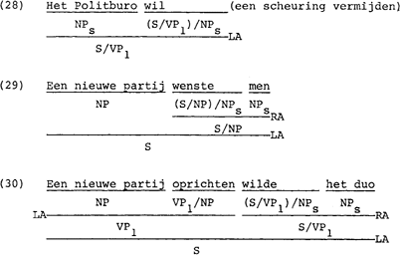
Links-applikatie bij deze groep funktoren is niet onbeperkt. In zin (31) zien we dat meervoudige toepassing van de regel ongrammatikaliteit oplevert.

We sluiten de zin uit d.m.v. het feature [αTOPIC]. De funktor heeft het feature [-TOPIC] voor de toepassing van de applikatie. De resultante krijgt het feature [+TOPIC] en is daarmee uitgesloten voor ver-

[p. 10]

dere deelneming aan de regel.

Niet alle kategorieën kunnen als argument bij deze groep funktoren optreden. De zinnen (32) en (33) laten zien dat VP₀ en VP₂ als argument uitgesloten moeten worden.

De behandelde voorbeelden rechtvaardigen het postuleren van de volgende regels.

LA	1	Y	VP/Y	VP →	, tenzij	Y=S̄
	2	Y	S$/Y →	S$	, tenzij	Y=VP0 of VP2
			[-TOPIC]	[+TOPIC]

2. Funktorkompositie

Bij funktorkompositie worden twee funktoren samengesteld tot één funktor. Als de noemer van de eerste funktor gelijk is aan de teller van de tweede funktor, dan bestaat de kategorie van de samengestelde funktor uit de teller van de eerste en de noemer van de tweede funktor. Ook als de funktoren in een andere volgorde staan is kompositie in principe mogelijk. Schematisch ziet het er als volgt uit:

a.	X/Y Y/Z → X/Z
b.	Y/Z X/Y → X/Z

Funktorkompositie is bv. nodig als tussen een funktor en zijn argument nog een andere funktor staat. We behandelen achtereenvolgens rechtse kompositie (2.1) en linkse kompositie (2.2).

[p. 11]

2.1. Rechtse kompositie

Bij rechtse kompositie hoort het bovenstaande regelschema a. Doordat in het Nederlands meerdere volgordes vaak een grammatikaal resultaat opleveren, wordt dit mechanisme veelvuldig gebruikt.

In (35) is X een variabele over alle kategorieën. In verband met de voegwoorden is een kleine aanpassing van LA nodig maar dat is voor dit betoog niet belangrijk.

[p. 12]

De voorbeelden wijzen uit dat de regel voor rechtse kompositie onbeperkt is.

2.2 Linkse kompositie

Linkse kompositie komt overeen met regelschema b onder 2.

De zinnen (38) t/m (43) wijzen erop dat deze regel slechts werkt als de hoofdfunktor, in dit regelschema de rechter funktor, van de vorm S$ is.

[p. 13]

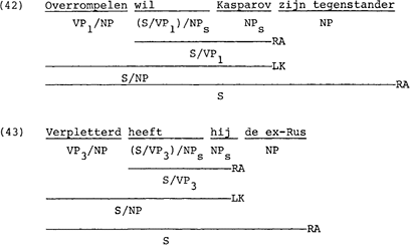
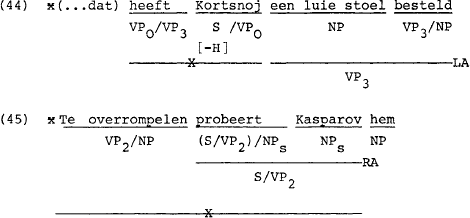
In (44) en (45) blijkt dat linkse kompositie uitgesloten moet worden als de tweede funktor van de vorm VP₀$ of VP₂$ is, en in (46) zien we dat we de regel ook moeten uitsluiten als de hoofdfunktor gespecificeerd is voor [+TOPIC]. Op grond daarvan hanteren we het feature [αTOPIC] zoals dat ook al bij LA (p. 9) gebruikt werd.

[p. 14]

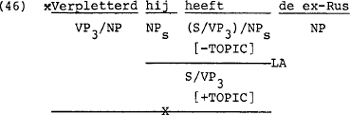
De regel voor linkse kompositie volgt nu onderaan in het overzicht van de tot nu toe ontwikkelde regels.

RA		X/Y	Y	→ X	,	tenzij X=VP en Y=NP
LA	1	Y	VP/Y	→ VP	,	tenzij Y=S̄
	2	Y	S$/Y	→ S$	,	tenzij Y=VP0 of VP2
			[-TOPIC]	[+TOPIC]
RK		X/Y	Y/Z	→ X/Z
LK		Y/Z	S/Y	→ S/Z	,	tenzij Y=VP0 of VP2
			[-TOPIC]	[+TOPIC]

Opvallend zijn de overeenkomsten tussen LA 2 en LK. Beide regels hebben de konditie dat Y niet VP₀ kan zijn en beide regels hebben een topic-restriktie. In de calculus van Lambek (1958; 1961) is de regel X/Y → (X/Z)/(Y/Z) afleidbaar, een versie van zijn kompositieregel, waaruit blijkt dat in zo'n systeem LK beschouwd kan worden als een speciaal geval van LA 2. De afleiding geschiedt op basis van de axioma's en de inferentieregels. In het regelschema dat hier ontwikkeld is, is een dergelijke afleiding niet mogelijk. Er gelden geen andere dan de gegeven regels. Bovendien rechtvaardigen de kondities op applikatie en kompositie zo'n algemene regel niet. De vergelijking met het systeem van Lambek laat echter wel zien dat de overeenkomsten tussen LA 2 en LK niet toevallig zijn.

3. Toetsing van het regelsysteem

In dit hoofdstuk worden de mogelijkheden van het hiervóór ontwikkelde regelsysteem getoetst aan een aantal weerbarstige verschijnselen. In 3.1 komen ‘extrapositie’ en ‘V-raising’ aan de orde, in

[p. 15]

3.2 Accousativus cum infinitivo en Infinitivus pro participio en in 3.3 wordt een metaregel geformuleerd die noodzakelijk is voor de afleiding van zinnen met V-klusters.

3.1 ‘Extrapositie’ en ‘V-raising’

3.1.1 Verplichte ‘extrapositie’

In deze paragraaf behandelen we zinnen waarin volgens transformationele grammatika's de transformatie extrapositie toegepast is. Door een juiste kategorisering van de verschillende elementen zijn de bovenstaande regels in staat de verplichte ‘extrapositie’ adekwaat te beschrijven.

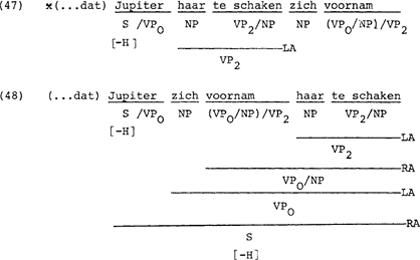
Twee werkwoorden, waarbij in een T.G. extrapositie verplicht is, zijn zich voornemen en dwingen. Door toekenning van de kategorie (VP₀/NP)/VP₂ aan voornemen en dwingen is de extrapositie-volgorde de enige acceptabele volgorde.

[p. 16]

Zin (49) wordt uitgesloten omdat zich hier niet als argument van voornemen fungeert maar als argument van te schaken en omdat haar het argument is bij voornemen. De uitsluiting kan geschieden door een feature [+WEDERKEREND] onder de NP-positie in de kategorie voor voornemen.

Dwingen gedraagt zich net als voornemen. We zien dit door in (47) t/m (49) zich te vervangen door hem en voornemen door dwingen.

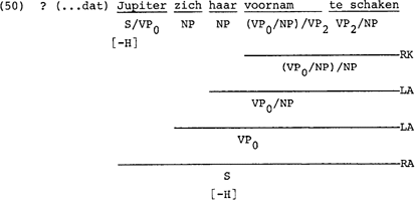
De volgende zin waarover ik geen duidelijk grammatikaliteitsoordeel heb wordt door het regelsysteem geaccepteerd.

3.1.2 ‘V-raising’ of ‘Extrapositie’

In sommige gevallen -weer in transformationele termen- is V-raising optioneel. In deze gevallen is extrapositie verplicht als V-raising niet optreedt. Proberen is een werkwoord waarbij dit van toepassing is.

[p. 17]

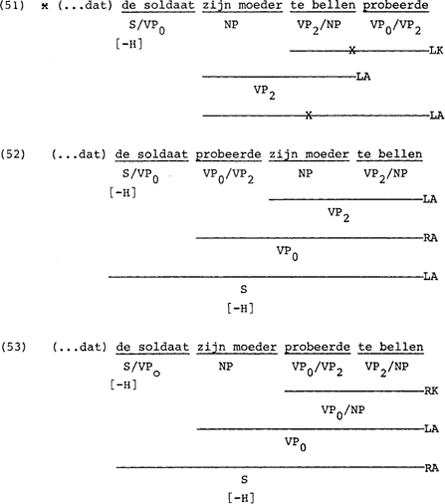
Als we willen zouden substitueren voor proberen (en te wordt geschrapt), dan zou alleen volgorde (53) grammatikaal zijn als gevolg van het feature [+L] in de argumentspositie van willen. We kunnen dus stellen dat (52) grammatikaal is door het ontbreken van een feature [αL] in de argumentspositie van proberen.

Zin (51) laat zien dat LA 1 nog de konditie nodig heeft dat Y ≠ VP₂.

[p. 18]

3.1.3 Verplichte ‘V-raising’ + te

Voor de beschrijving van verplichte V-raising + te is het nodig de argumentsposities van de betreffende werkwoorden te voorzien van het feature [αL]. Het gaat om werkwoorden als dienen, die in de volgordes van (51) en (52) een ongrammatikale zin opleveren en alleen in de volgorde van (53) een korrekt resultaat te zien geven. Een illustratie hiervan zien we in (54) t/m (56).

3.1.4 ‘V-raising’ met losse infinitieven als komplement

Voorbeelden hiervan worden gevonden in zinnen met de uitdrukking

[p. 19]

zich laten gaan. Door laten te kategoriseren als (VP₁/NP)/VP₁ wordt (57) korrekt beschreven. De motivatie voor juist deze kategorisering voor laten komt in 3.2 aan de orde.

3.2 Twee verschijnselen

3.2.1 Accusativus cum infinitivo

De volgende konstruktie staat traditioneel bekend onder de term accusativus cum infinitivo.

(58)	Ik zie haar lopen

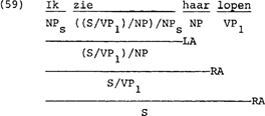
Haar is het logisch objekt bij zien en het logisch subjekt van lopen. Haar en lopen kunnen niet in een funktierelatie tot elkaar staan. Dit is het gevolg van het feit dat lopen een niet vervoegde vorm is en daarom de kategorie VP₁ toegekend krijgt. Haar is, gezien de objektsvorm waarin het staat, een argument bij zien. De oplossing voor deze konstruktie is dat ook lopen een argument bij zien is. Eenzelfde soort redenering geldt voor zin (57) in 3.1.4 waarbij zich, laten en gaan respektievelijk vergeleken moeten worden met haar, zien en lopen. We krijgen nu de analyse:

[p. 20]

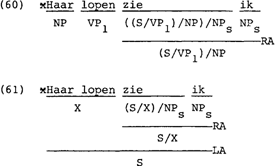
Door deze analyse kunnen we nu verklaren waarom (60) ongrammatikaal is. Als haar en lopen in een funktierelatie tot elkaar stonden, dan was de woordgroep haar lopen van een bepaalde kategorie, zeg X, maar dan zou de struktuur in (61) het regelsysteem niet in staat zijn de zin uit te sluiten.

3.2.2 Infinitivus pro participio

Het verschijnsel infinitivus pro participio wordt gekenmerkt door het feit dat, daar waar de aanwezigheid van een hulpwerkwoord van tijd tevens de aanwezigheid van een voltooid deelwoord suggereert, de plaats van dit deelwoord ingenomen wordt door een infinitief.

(62)	De spookrijder heeft de tegenliggers zien aankomen

Om de berekening in orde te krijgen moeten we recht doen aan onze intuïties dat zin(62) weergeeft dat de spookrijder gezien heeft dat er tegenliggers aankwamen m.a.w. dat zien in feite een voltooide tijd aangeeft. Zien krijgt (o.a.) de kategorie (VP₃/NP)/VP₁[+L]. (VP₃/VP₁ [+L])/NP voldoet niet omdat LA niet werkt op funktoren van de vorm VP$/NP.

Zin (62) geeft met gezien op de plaats van zien een ongrammatikaal resultaat. De theorie verantwoordt dit door als enige kategori-

[p. 21]

seringen voor gezien toe te laten: VP₃/NP en VP₃/S̄.

Andere voorbeelden van de infinitivus pro participio-konstruktie zijn (63) en (64).

Voor proberen en geprobeerd moeten in dit verband de volgende kategoriseringen gelden (ga dit na voor (65) t/m (69)):
proberen ↑ VP₃/VP₂[+L]; geprobeerd ↑ (VP₃/NP, VP₃/VP₂)

(65)	Hij heeft haar proberen te bellen
(66)	x̶Hij heeft proberen haar te bellen
(67)	Hij heeft het geprobeerd
(68)	Hij heeft geprobeerd haar te bellen
(69)	Hij heeft geprobeerd haar te bellen

3.3 V-klusters

We hebben bij zin (62) gezien dat de keuze van de kategorie voor zien o.a. bepaald werd door de blokkade van de linkse applikatie voor funktoren van de vorm VP$/NP (waarbij $ in dit geval niet nul is).

[p. 22]

We kunnen ons afvragen of regel LA verruimd moet worden om deze applikatie toe te staan. We zouden dan analyse (70) hebben i.p.v. (71).

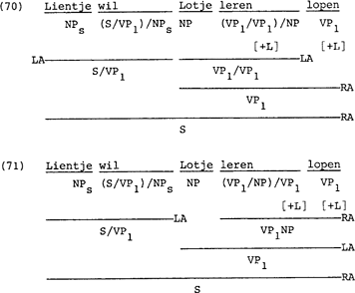
In (72) blijkt echter dat de kategorie (VP₁ VP₁+L]) /NP tot gevolg heeft dat deze ongrammatikale zin geaccepteerd wordt. Bij de kategorisering (VP₁/NP)/VP₁[+L] in (73) wordt de zin geblokkeerd.

In (74) wordt een grammatikale zin niet geaccepteerd, die volgens de kategorisering in (75) niet geblokkeerd wordt. Op grond hiervan is de kategorisering van leren in (73) en (75) beter en is een verruiming van de regel voor linkse applikatie niet nodig.

[p. 23]

Bij de beschouwing van grotere V-klusters als in (76) stuiten we op een probleem. De bestaande regels kunnen de zin niet afleiden.

[p. 24]

De regel van Lambek die in paragraaf 2.2 genoemd werd, X/Y → (X/Z)/(Y/Z), zou er voor zorgen dat zin (76) afgeleid kan worden. In dezelfde paragraaf hebben we echter ook gezien dat op grond van de beperkingen die opgelegd zijn aan de regels, zo'n algemene regel niet kan gelden.

We kunnen echter met behulp van de volgende regel de zin afleiden. De regel zullen we hier metaregel (MR) noemen, omdat er sprake is van kategoriewisseling van elementen en niet van kategoriebepaling van samengevoegde elementen.

[p. 25]

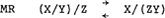
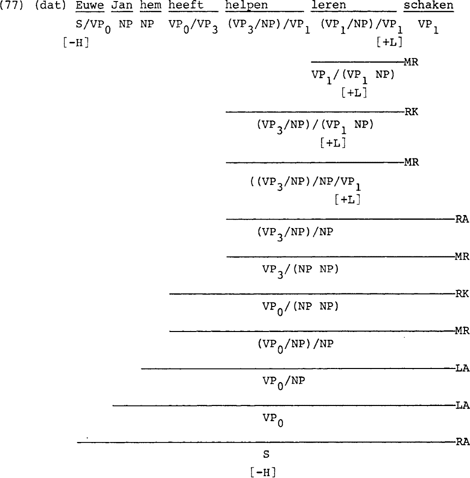
Zin (78) lijkt voor moeilijkheden te gaan zorgen. Weliswaar is de rechtsapplikatie van helpen schaken en Jan niet mogelijk, maar door de metaregel lijkt de volgende analyse niet te vermijden.

[p. 26]

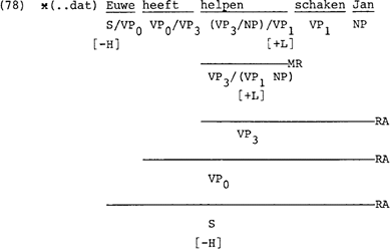
De hier ontwikkelde regels laten evenwel geen applikatie toe van meerdere elementen tegelijk. Een kategorie X/(Z Y) zal dus altijd eerst omgezet moeten worden in (X/Y)/Z voordat applikatie met de argumenten Y en Z kan plaatsvinden.

Als men een systeem kiest waarin wel meervoudige applikatie mogelijk is, dan is de konditie nodig dat in de regel VP/(Z Y) Z Y → VP, Y en Z geen NP mogen zijn.

Noten

Graag bedank ik Ineke Schuurman, Jack Hoeksema, Marjan van den Hoek en Ron van Zonneveld voor hun aandeel in de totstandkoming van dit artikel.

Bibliografie

Ades, A.E. & M.J. Steedman (1982)	‘On the order of words’. In: Linguistics and Philosophy 4, p. 517-558
Flynn, M.J. (1981)	Structure building operations and word order, dissertatie, University of Massachusetts.
Hoeksema, J. (1980)	‘Verbale verstrengeling ontstrengeld’. In: Spektator 10.3. p. 221-249

[p. 27]

Lambek, J. (1958)	‘The mathematics of sentence structure’. In: American Mathematical Monthly 65, p. 154-169
Lambek, J. (1961)	‘On the calculus of syntactic types’. In: R. Jakobson (ed) Structure of language and its mathematical aspects, Providence
Levelt, W.J.M. (1973)	Formele grammatica's in linguistiek en taalpsychologie, deel II, Deventer
Montague, R. (1973)	‘The proper treatment of quantification in ordinary English’. In: K.J.J. Hintikka, J.M.E. Moravcsik & P. Suppes (eds), Approaches to Natural Language, Dordrecht, p. 221-242
Steedman, M.J. (1983)	A categorial syntax for subject and tensed verb in English and some related languages. Paper University of Warwick