Tabu. Jaargang 12

[p. 86]

Enkele stellingen omtrent metrische representaties
J. Hoeksema

Sinds enkele jaren hebben veel fonologische artikelen een ander uiterlijk gekregen. Reeds bij de eerste vluchtige blik vallen de metrische boompjes op, die door de tekst zijn gestrooid. Het is voor mij, als betrekkelijke buitenstaander op dit terrein, verbazingwekkend dat er voor het verschijnen van Liberman & Prince (1977) zo weinig en erna zo buitengewoon veel is gewerkt met hiërarchische metrische strukturen. Men kan zich, met Van Zonneveld (1982) afvragen, of de ouderwetse methode van cijfertoekenning aan vokalen echt zo veel slechter is als welke metrische theorie dan ook - maar dat wil ik hier niet doen. Wat mij hier interesseert is een meer abstrakte vraagstelling, namelijk, in hoeverre een representatie in de vorm van een metrische boomstruktuur en een representatie in de vorm van een reeks cijferwaarden onderling vertaalbaar zijn. Wanneer zou blijken, dat dit heel goed mogelijk is, dan betekent dat niets minder, dan dat beide representaties in principe gelijkwaardig zijn, zoals ook bijvoorbeeld een boomstruktuur en een benoemde haakjesstruktuur gelijkwaardige representaties zijn. Daarmee is vanzelfsprekend nog niet gezegd dat de twee representaties ook even bruikbaar of doorzichtig zijn - dat is een zaak die de gebruikers, i.c. de fonologen moeten beslissen.

Hoewel ik in het merendeel van mijn betoog gebruik zal maken van de metrische strukturen die Liberman & Prince hebben voorgesteld, kunnen de konklusies ook worden uitgebreid naar alternatieve metrische theorieën, die doorgaans gebruik maken van een rijker nonterminaal vokabularium. Liberman & Prince maken gebruik van metrische strukturen die zich laten karakteriseren door het nonterminale vokabularium¹ {R, S, W} en de herschrijfregels

(1)	a.	R → a (waar α een willekeurig terminaal element is)
	b.	R → S W
	c.	R → W S
	d.	S → W S
	e.	S → S W
	f.	W → S W
	g.	W → W S
	h.	S → a
	i	W → a

1 R staat voor root, S voor strong en W voor weak. R is het startsymbool.

[p. 87]

Elke metrische representatie die welgevormd is, is een struktuur die wordt gegenereerd door de bovenstaande regels. Om misverstanden te voorkomen: niet elke struktuur die door de regels in (1) wordt gegenereerd is een akseptabele metrische struktuur. Liberman & Prince maken gebruik van knooptoelaatbaarheidsprincipes als ‘a right node is strong iff it braoenes om uit de overdaad door (1) geschapen de relevante deelverzameling van akseptabele metrische strukturen te halen. Aangezien mijn stellingen voor alle door (1) gegenereerde atrukturen opgaan, gaan ze uiteraard ook op voor de genoemde deelverzameling.

Een voorbeeld van een metrische struktuur is:

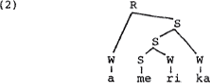
Het aksentpatroon van het woord Amerika, in (2) weergegeven in de vorm van een metrisch boompje, zou in een SPE-achtig kader als volgt zijn weergegeven:

(3)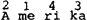

In Liberman & Prince (1977: 259) wordt een eenvoudig algoritme gegeven dat op basis van een metrische boomstruktuur als in (2) de bijbehorende getallenrepresentatie in (3) uitrekent:

(4)	‘If a terminal node t is labeled w, its stress number is equal to the number of nodes that dominate it, plus one. If a terminal node t is labeled s, its stress number is equal to the number of nodes that dominate the lowest w dominating t, plus one.’

Liberman & Prince presenteren dit algoritme min of meer terloops en hechten er geen enkele theoretische waarde aan. Dit is zonder meer terecht, want de afbeelding op een getallenrepresentatie geeft slechts een ruwe weergave van de oorspronkelijke metrische struktuur. Dit blijkt onder andere uit hun voorbeeld (13), hier herhaald als (5):

[p. 88]

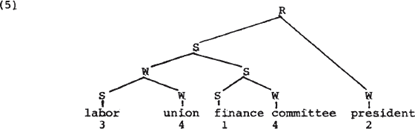
Men ziet hoe in dit geval aan twee woorden dezelfde waarde is toegekend, hoewel uit de metrische struktuur valt af te leiden dat ze niet dezelfde status hebben: union wordt immers gedomineerd door 2 W-knopen, terwijl committee door slechts 1 W-knoop wordt gedomineerd.

Ernstiger nog is in mijn ogen het feit dat de inverse van het algoritme geen funktie is. Anders gezegd, er kunnen met een gegeven getallenrepresentatie meerdere metrische strukturen korresponderen. Laat ik dit illustreren aan de hand van de twee strukturen in (6):

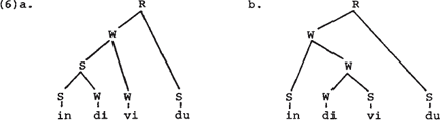
Volgens algoritme (4) komen beide metrische strukturen overeen met een en dezelfde getallenrepresentatie, namelijk:

(7)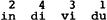

Men kan zich afvragen of een getallenrepresentatie in het algemeen niet minder zegt dan een hiërarchische representatie in de vorm van een metrische boomstruktuur. Dit blijkt echter niet het geval te zijn. Er bestaat een elegante en eenvoudige methode om in een aantal stappen van een metrische boomstruktuur een getallenrepresentatie af te leiden en vice versa. Hiertoe maken we gebruik van een formele eigenschap van het soort strukturen dat door de regels in (1) wordt gegenereerd. Deze strukturen worden namelijk volledig gekenmerkt door de verzameling van alle paden van terminale knopen naar de topknoop of wortel, geordend volgens

[p. 89]

de links-rechts volgorde van de terminale knopen. Om een voorbeeld te geven; de metrische atruktuur in (8) is isomorf met de geordende verzameling van zijn blad-naar-wortel paden in (9):

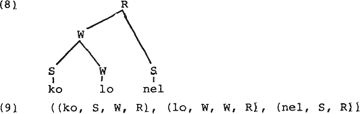
Laten we verwijzen naar een representatie als in (9) van een boom A met P(A). Nu kunnen we de bedoelde eigenschap van metrische boomstrukturen verwoorden in de volgende stelling:

(10)	Pad-Boom Stelling
	Elke metrische boom A wordt uniek gekarakteriseerd door P(A), de geordende verzameling van zijn blad-naar-wortel paden.

De Pad-Boom stelling is niet triviaal, omdat er strukturen zijn, die er niet aan voldoen. Beschouw de twee strukturen in (11).

Beide boomstrukturen hebben precies dezelfde paden. Een grammatika die zowel (11)a als (11)b genereert voldoet dus niet aan de Pad-Boom Stelling, of, anders gezegd, heeft niet de Pad-Boom eigenschap.

Hoe weten we nu wanneer een gegeven grammatica de Pad-Boom eigenschap heeft? Dit wordt uiteengezet in de volgende stelling.

(12)	Stelling
	Een herschrijfgrammatika G heeft de Pad-Boom eigenschap als elke produktieregel van de vorm A → α1...αn is, waar αi ≠ αi+1 voor elke i, zodanig dat 1 ≤ i<n, A een hulpsymbool en αi een hulp- of eindsymbool is.^2

Ga na dat de grammatika in (1) voldoet aan de eisen die in bovenstaande stelling worden genoemd. In feite voldoet elke

2 Men kan zich afvragen of de implikatie in stelling (12) kan worden aangesterkt tot een ekwivalentie. Dit is niet het geval. Men neme een simpel tegenvoorbeeld, en het wordt duidelijk waarom: de grammatika met produktieregels R → AA, A → a en R als startsymbool. Deze grammatika genereert de taal {aa} en heeft de Pad-Boom eigenschap, hoewel hij niet voldoet aan de eisen in (12) Dit komt omdat aa, de enige zin van de taal, niet ambigu is, en dus maar één struktuur heeft:

(1)		R
	A		A
	a		a

[p. 90]

metrische theorie er aan, aangezien de knopen relationeel geïnterpreteerd worden. Een konfiguratie als [WW] of [SS] wordt expliciet uitgesloten (cf, Liberman & Prince 1977: 256), omdat W geïnterpreteerd wordt als: zwakker dan haar zuster. De konfiguratie [WW] zou dan gelezen moeten worden als: de zusterknopen zijn zwakker dan elkaar - een paradox. Aangezien deze relationele interpretatie alle mij bekende metrische theorieën aankleeft, mag stelling (10), de Pad-Boom Stelling, als gerechtvaardigd worden beschouwd.

Nu moet ik nog aantonen dat stelling (12) korrekt is. Dit gaat waarschijnlijk het gemakkelijkst met een plaatje. Nemen we een willekeurige boom A:

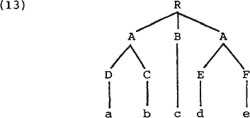
We kunnen P(A) als volgt representeren in de vorm van een diagram, waarbij de kolommen overeen komen met de paden:

Vervolgens moeten we laten zien, dat een diagram zoals (14) op een unieke wijze om te zetten valt in boomstrukturen als (13). Hiervoor gebruiken we de volgende methode. Werk de horizontale rijen van boven naar beneden af en zet een scheidingsstreep tussen voorkomens van ongelijke symbolen. Trek de scheidingslijnen door naar onderen. Deze methode levert voor diagram (14) het volgende aangepaste diagram op;

[p. 91]

We hebben nu per kolom maximaal ononderbroken reeksen van hetzelfde symbool. Een dergelijk diagram laat zich heel eenvoudig afbeelden op een boomdiagram: laat elke maximaal ononderbroken reeks van het symbool α korresponderen met een knoop met het label α in de boomstruktuur. Wanneer twee maximaal ononderbroken reeksen α...α en β...β een kolom gemeen hebben, en α...α zit in een hogere horizontale rij dan β...β dan domineert in de boomstruktuur de knoop α, die het korrelaat is van de rij α...α in het diagram, de knoop β die het korrelaat is van de rij β...β.

Het valt nu ook gemakkelijk in te zien, waarom produkties van de vorm A → ...αⁱα^j..., waarbij α_i = α_j uitgesloten dienen te worden in stelling (12). Immers, als er bij het konstrueren van een boom gebruik is gemaakt van een dergelijke produktie, dan is er een horizontale rij in het diagram van zijn paden, waarin een maximaal ononderbroken reeks symbolen α...α overeen komt met twee knopen in de boom, nl. α_i en α_j, in plaats van met precies een knoop.

Hiermee is de geldigheid van stelling (12) voor onze doeleinden afdoende aangetoond. We gaan nu over naar de volgende stap in ons betoog.

Ik heb laten zien, dat een metrische boomstruktuur volledig gekarakteriseerd wordt door de geordende verzameling van paden van bladeren naar de wortel. Dit houdt in, dat een representatie waarin elk terminaal element als kenmerk het pad van de hem direkt dominerende knoop naar de top meekrijgt ekwivalent is aan de representatie in de vorm van een metrische boom. Dus:

(16)	ko(S, W, R) lo(W, W, R) nel(S, R)

in plaats van (8). Aangezien R steeds het laatste element is in elk kenmerk, kunnen we het per konventie weglaten. Dit geeft ons in plaats van (16) de volgende representatie:

[p. 92]

(17)	ko(S, W) lo(W, W) nel(S)

Omdat we op zoek. waren naar een getallenrepresentatie vervangen we vervolgens elke S door O en elke W door 1. Dit levert een representatie met getallen in het tweetallig stelsel³ op:

(18)	ko(01) lo(11) nel (O)

Getallen in het tweetallig stelsel kunnen we omzetten in getallen in het tientallig stelsel. Resultaat:

(19)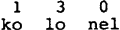

Als laatste stap tellen we bij ieder getal 1 op, zodat het hoofdaksent overeenkomt met het kenmerk 1:

(20)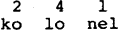

Hiermee is het bestaan aangetoond van een tamelijk simpel algoritme van hiërarchische metrische representaties naar getallenrepresentaties en vice versa. We drukken dit uit in de volgende stelling:

(21)	Stelling
	Er bestaat een bijektie tussen hiërarchische metrische strukturen en getallenrepresentaties à la SPE.

Voor metrische theorieën die meer prosodische kategorieën toestaan dan Liberman & Prince moet als tussenstap niet van binaire getallen gebruik gemaakt worden, maar van getallen in het n-tallig stelsel - waar n het aantal hulpsymbolen is. Zolang het aantal prosodische kategorieën eindig is, kan men dus altijd een representatie met natuurlijke getallen geven.

Om een indruk te geven van het soort cijferwaarden dat mijn algoritme toekent aan terminale eindrijen zal ik het toepassen op voorbeeld (5). We krijgen dan:

(22)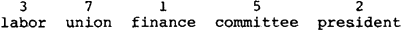

Men kan zich natuurlijk afvragen of dit nog wel ‘realistische’ representaties zijn, aangezien een waarde als 7 wel erg hoog lijkt. Er is echter niets tegen om de cijferwaarden als zuiver relatief te interpreteren - zoals Van Zonneveld (1982) voorstelt. De cijferwaarde van union dient dan enkel om aan te geven dat dit woord zwakker benadrukt is als alle andere. In dat

3 Crit Cremers heeft me gewezen op een probleem in verband met binaire getallen dat ik aanvankelijk over het hoofd had gezien. In het tweetallig stelsel zijn 0001, 001, 01 en 1 ekwivalent.
Niettemin is het aantal nullen voor de eerste 1 wel degelijk van belang voor het bepalen van het bijbehorende pad. Gelukkig valt dit aantal in alle gevallen te rekonstrueren, zij het enigszins moeizaam. We kunnen een funktie definiëren die voor elk binair getal in een fonologische representatie de relevante rij nullen en enen aflevert.
Laat i₁...i_n een reeks binaire getallen zijn in normaalvorm (dwz.: i_k is 0 of begint met een 1, voor elke k, 1 ≤ k ≤ n), die geassocieerd is met een reeks fonologische eenheden a₁...a_n. Laat c_n (i) staan voor de rij van de laatste n cijfers van i. Laat voorts |i| het aantal cijfers van i zijn. Laat m het grootste getal zijn, zodanig dat c_m(i_k) = c_m(i_k+1) of c_m(i_k-1). Neem eerst het geval dat c_m(i_k-1) ≠ c_m(i_k Dan definiëren we: V(i_k) 0^c_p-1(i_k+1), waar c_p(i_k+1) = 1^0*^c_m(i_k+1), indien m = |i_k| en V(i_k) = i_k in het andere geval. Het geval waar c_m(i_k+1) ≠ c_m(i_k) gaat analoog, met verwisseling van k-1 en k+1. In het geval dat c_m(i_k-1) = c_m(i_k+1) definiëren we: V(i_k) = 0^c_p-1(i_k-1) waarbij c_p als boven - indien |c_p(i_k-1)| > |c_p(i_k+1)| en tevens m = |i_k|. Indien echter c_p(i_k+1) > |c_p(i_k-1)| en m = |i_k|, dan definiëren we: V(i_k) = 0^ c_p-1 (i_k+1). Indien m ≠ |i_k|, dan geldt: V(i_k) = i_k. Ga na, dat |c_p(i_k+1)| = |c_p|(i_k-1)| is uitgesloten wegens maximaliteit van m.

[p. 93]

geval maakt het niets uit, of union de waarde 7 krijgt, of 77. Overigens kan men aan (22) ook zien, dat roijn bezwaar tegen het numeriek gelijkstellen van union en committee volgens het algoritme van Liberman & Prince is ondervangen.

Hiermee ben ik bijna aan het slot van mijn verhaal gekomen. Ik heb mij in het voorgaande gekoncentreerd op de onderlinge vertaalbaarheid van twee representaties voor aksentpafcronen. Niets heb ik gezegd over regels. Het ligt echter voor de hand - gezien de gelijkwaardigheid van de twee systemen - dat regels die zijn geformuleerd voor hiërarchische systemen ook te gebruiken zijn in numerieke systemen. Het is dan wel zo gemakkelijk om gebruik te maken van binaire getallen. Laat me ter illustratie het voorbeeld van de Lexiaal Category Prominenee Rule geven (cf. Liberman & Prince 1977: 304):

(23)	LCPR: in a metrical configuration [N1, N2], N2, is strong iff it branches.

Aangezien vertakking bij Liberman & Prince - en meer in het algemeen bij alle systemen in de Chomsky-normaalvorm - gelijk staat aan het niet direkt domineren van terminale elementen, kunnen we de volgende herformulering in ons binaire numerieke systeem overwegen:

(24)

LCPR (numeriek): laat a (..,ω) en b (..,ω) twee aangrenzende elementen zijn, met a links van b en ω de maximale rij over {0, 1} die a en b aan de staart van hun numerieke kenmerk gemeen hebben. Nu geldt: a heeft het numerieke kenmerk (.., 0, ω) dan en slechts dan als b het numerieke kenmerk (l, ω) heeft.

[p. 94]

(Vakgroep Nederlandse Taalkunde, RU Groningen)

[p. 95]

Verwijzingen

Booij, G.E.,
(1977)	Dutch Morphology. Lisse.
(1978)	‘Fonotactische restricties in de generatieve fonologie’. Spektator 9, 29 - 46.
(1982)	‘Hiërarchische fonologie’. Oratie, Amsterdam.
Chomsky, N. en M. Halle,
(1968)	The Sound Pattern of English. New York.
Dijkstra, J.M.,
(1981)	‘De stress scale’. Ongepubl. werkstuk, ATW Groningen.
Kahn, D.,
(1976)	Syllable-based generalisations in English phonology. IULC.
Kiparsky, P.,
(1966)	‘Ueber den Deutschen Akzent’. Studia Grammatica VII, 69 - 98.
Liberman, M. en A. Prince,
(1977)	‘On stress and linguistic rhythm’. Linguistic Inquiry 8:2, 249 - 336.
Montague, R.,
(1974)	Formal Philosophy. Uitgegeven door R, Thamason, New Haven en Londen.
Nes, J.J. van,
(1981)	‘Een klemtoonpatroon voor het nederlands’. Ongepubl. werkstuk, ATW Groningen.
Neijt, A. en W. Zonneveld,
(1981)	‘De aantrekkingskracht van -baar’. GLOT 4:2, 215 - 228.
Selkirk, E.O.,
(1980)	‘The role of prosodie categories in English word stress’. Linguistic Inquiry 11:3, 563 - 605.
Wheeler, D.W.
(1981)	Aspects of a categorial theory of phonology. Ongepubl. diss., Univ. of Massachusetts at Amherst.
Zonneveld, R.M. van,
(1980)	‘De hoofdaccentregel, stressers, strippers, magneten en een ritmische hangmat’. Th. Janssen en N.F. Streekstra (red.), Grenzen en Domeinen in de grammatica van het Nederlands, Groningen, 181 - 205.
(1982)	in dit nummer.