De Nieuwe Taalgids. Jaargang 70
(1977)– [tijdschrift] Nieuwe Taalgids, De–
[pagina 541]
| |||||||||||||||
Tussen taalkunde en filosofieGa naar voetnoot*I. Semantiek in de taalkunde en filosofie0. Inleiding.De titel van dit artikel is een reflectie van de titel van een boek dat ik ter recensie kreeg voorgelegd. Het boek is geschreven door Pieter A.M. Seuren en heet Tussen taal en denken; een bijdrage tot de empirische funderingen van de semantiek. Het verscheen bij Oosthoek, Scheltema & Holkema te Utrecht in 1975 en telt 345 bladzijden. Het is een moeilijk boek. Dat is toe te schrijven aan de ingewikkeldheid van de behandelde stof, maar ook aan de ingewikkelde behandeling van die stof. Bij de presentatie van zijn ideeën schuwt Seuren de polemiek niet. Er is veel degengekletter met illustere tegenstanders die het volle pond krijgen. Daardoor wordt het zicht op wat Seuren werkelijk te vertellen heeft soms wat verduisterd. De keuze is in zo'n geval òf het boek zeer oppervlakkig te bespreken òf nader in te gaan op de gestelde problemen. In het laatste geval krijgt de reactie op een boek een voorlichtend en organiserend aspect, en op basis daarvan een kritisch-evaluerend aspect. De huidige stand van zaken op het gebied van de theorievorming over semantiek geeft aanleiding tot een beschouwing waarbij het eerste aspect nogal sterk wordt belicht voordat het tweede aspect aan de beurt komt. Dit artikel valt in twee delen uiteen. Het eerste deel bevat, na een korte oriëntatie op de hoofdzaken van Seurens boek, een overzicht van belangrijke ontwikkelingen in de semantische theorievorming zowel in de taalkunde als in de filosofische logica. Tegen de achtergrond van dit overzicht volgt dan in het tweede deel een nadere bespreking en evaluatie van Seurens positie. Deel I kan dus zelfstandig gelezen worden. Deel II verschijnt in de volgende aflevering. Daarin is ook de bibliografie opgenomen. | |||||||||||||||
1. Tussen taal en denken?Met de titel van het boek - of liever, met de suggestie die er van uitgaat - heb ik nogal wat moeite. Seuren situeert zijn werk in een tussengebied en vertrekt vanuit een empirisch vak, de taalkunde. De ondertitel geeft aan dat hij een empirische kant uit wil gaan. Men verwacht dan ook aan de andere zijde van de brug tussen taal en cognitie een empirische bedrijvigheid, zoals onderzoek naar het geheugen, of iets algemener, onderzoek van informatieverwerkende systemen, of onderzoek binnen de cognitieve psychologie. Seuren heeft zijn werk echter bewust gesitueerd tussen taalkunde en filosolfie (p. XIX). Onder dit laatste valt wat men wel aanduidt met de termen ‘logische semantiek’ en ‘filosofische logica’. Een ontmoeting dus tussen een empirisch vak en een niet-empirisch vak, wat - gezien de empirische doelstelling - wel ten voordele van de taalkunde moet uitvallen. Daarmee kent Seuren de taalkunde (of liever, zijn taalkunde) een voortrekkersrol toe die vooral daar speelt waar cognitief-psychologische kwesties aan de orde komen. Zeer globaal en nog voorlopig geformuleerd gaat het in het boek om het volgende. Seuren is niet tevreden met de manier waarop binnen het transformationele kader | |||||||||||||||
[pagina 542]
| |||||||||||||||
semantiek wordt bedreven. Hij wendt zich tot de filosofie waar veel aan semantiek is gedaan, met name bij de constructie van formele talen. Semantiek houdt er in het interpreteren van syntaktische systemen, ook wel calculi genoemd, met het oog op de toepassing van dergelijke systemen op (een deel van) de werkelijkheid. De relatie tussen elementen van dergelijke calculi en de werkelijkheid waarover men wil spreken, heeft in deze semantiek veel aandacht. Omdat deze relatie wel gezien wordt als een verwijzingsrelatie, spreekt men wel van ‘referentiële semantiek’. Seuren nu is van mening dat hij beschikt over een bruikbaar syntaktisch systeem - namelijk een generatief-semantische syntaxis - dat hem meer in de buurt brengt van de logische semantiek dan enige taalkundige semantiek. De logische semantiek wordt echter nogal gedomineerd door een filosofische stroming, het empirisme, terwijl transformationalisten doorgaans rationalistisch geöriënteerd zijn (vaak gebruiken deze laatsten de term ‘mentalisme’ om hun filosofische gezindheid te openbaren). Allerlei noties uit de logische semantiek zijn door genoemde empiristische dominantie besmet en moeten worden herzien in het licht van de doelstelling die Seuren aan zijn semantische theorie heeft meegegeven. Het eigenlijke probleem van de semantiek is voor Seuren de vraag ‘Hoe komt het dat we de zinnen van onze taal verstaan, zoals we ze verstaan?’. Semantische representaties (SR) van zinnen zijn bij Seuren uitdrukkingen uit een generatief-opgezette calculus, de zgn. semantische syntaxis. Hun interpretatie ligt niet in de werkelijkheid an sich, maar in de mentale sfeer. Spreekt een empirist over toepassingsgebied waarin hij de entiteiten die hij in zijn ontologie toelaat, herbergt, een mentalist zal hier liever werken met mentale ruimtes. Heeft een empirist het over een entiteit in de werkelijkheid, een mentalist zal spreken over de mentale representatie van die entiteit, etc. Deze mentalisering van de referentiële semantiek waarbij de geïdealiseerde spreker-hoorder bovendien wordt geduwd in de richting van een taalgebruiksmodel (de mentale ruimte heeft een tijdsas en een geheugen), levert volgens Seuren empirische winst op. Allerlei tekortkomingen in logische analyses van natuurlijke taal kunnen worden verbeterd. De mentalistische oplading van allerlei noties uit de referentiele semantiek brengt Seuren nu zeer dicht in de buurt van de cognitieve psychologie: hij moet zich immers - gezien zijn hoofdvraag - bezighouden met wat zich in het hoofd afspeelt. Daarmee verricht hij verkennend onderzoek in die richting. Maar juist hier wreekt zich de opgelegde beperking, want waar Seuren zich een moeizame weg baant door het struikgewas van de menselijke cognitie, waren al ettelijke wegen uitgezet in een gebied dat o.a. door Levelt (1973III) reeds samenvattend was beschreven. Op het globale niveau waarop ik thans de hoofdlijn van Seurens betoog bespreek, doen zich drie punten voor waar Seuren kritiek kan verwachten, behandeld in deel II. Het eerste punt betreft de presentatie van zijn argumenten ten gunste van zijn versie van de generatieve semantiek. Al discussiërend met Chomsky ontwikkelt Seuren zijn semantische syntaxis als basis voor zijn semantische theorie. Van transformationele zijde is mogelijk kritiek te verwachten op de weergave van allerlei kwesties en op de voorstellen betreffende de inrichting van de syntaxis van een natuurlijke taal. Dit punt betreft de eerste twee hoofdstukken die ongeveer een-derde van het boek in beslag nemen. In paragraaf 3 zal mijn bespreking van het boek zich daarop richten. Het tweede punt betreft het gedeelte van het boek waar Seuren uitvoerig ingaat op | |||||||||||||||
[pagina 543]
| |||||||||||||||
twee problemen die volgens hem de referentiele semantiek achtervolgen sinds Frege ze stelde door aan te tonen dat referentie en betekenis niet te identificeren zijn. Aan de hand van discussie over voorstellen tot oplossing van deze problemen brengt Seuren de lezer op de hoogte van een aantal opvattingen in de filosofische logica. Mogelijke kritiek op dit punt zal zich richten op de vraag of de weergave van wat zich in de filosofisch-logische literatuur als belangrijke problematiek aandient, correct, overzichtelijk en voldoende is. In paragraaf 4 zal mijn bespreking van het boek zich daarop richten. Het derde punt betreft de ontwikkeling en de illustratie van Seurens eigen semantische theorie. De vraag hierbij is of Seuren een werkelijk alternatief te bieden heeft voor bestaande theorieën. In paragraaf 5 zal ik deze vraag aan de orde stellen. | |||||||||||||||
2. Linguïstische en semiotische betekenisopvattingen.Het is mijn bedoeling in deze paragraaf een aantal termen te verduidelijken die in alle discussies over belangrijke semantische kwesties gehanteerd worden of op de achtergrond worden voorondersteld. Deze verduidelijking is nodig om een aantal redenen. Ten eerste heerst er veel verwarring waardoor allerlei begrippen door elkaar gaan lopen. Alleen daarom is het al gewenst te proberen allerlei begrippen eens precies op een rijtje te zetten. Ten tweede wordt het beter mogelijk bepaalde belangwekkende ontwikkelingen in de semantische theorievorming van de laatste tijd te schetsen. Ten derde kan de waarde van Seurens boek tegen de achtergrond van de gegeven schets beter worden geschat. De termen die in de loop van deze paragraaf zullen worden toegelicht, hebben een interpretatie die bepaald wordt door de invalshoek tot semantische theorievorming. Maar deze kan filosofisch, technisch, disciplinair of van andere aard zijn. Zo figureren er in de vakliteratuur opposities als:
Mijn bedoeling is vanuit een bepaald gezichtspunt de genoemde opposities te verduidelijken. Dit gezichtspunt houdt in dat elke semantische theorie semiotisch moet worden doorgelicht. | |||||||||||||||
2.1. De semiotische traditie.Onder semiotiek versta ik hier de algemene theorie van tekens en systemen van tekens (ofwel talen), zoals die vooral in en door het werk van Carnap (o.a. in Carnap 1958) vorm heeft gekregen. De term ‘taal’ heeft betrekking op formele èn natuurlijke talen. De bedoelde theorie is algemeen omdat men wil generaliseren over alle denkbare en feitelijke talen. Een taal wordt daarbij gezien als een systeem van tekens die uitdrukkingen van een bepaalde taal vormen. Deze uitdrukkingen hebben betrekking op datgene waarover men met behulp van de taal in kwestie wil praten. | |||||||||||||||
[pagina 544]
| |||||||||||||||
Een essentieel uitgangspunt is daarbij een zeer strenge, principiële scheiding tussen het systeem van tekens enerzijds en de interpretatie van die tekens anderzijds, tussen syntaxis en semantiek. De gedachte die hier aan ten grondslag ligt is dat tekens (symbolen) dienen te worden beschouwd als dingen die op zichzelf genomen niets betekenen. Net als gekleurde kralen kun je ze aaneenrijgen in bepaalde configuraties. Het spreekt bijna vanzelf dat bij de ontwikkeling van formele talen de vrijheid tot manipuleren van betekenisloze symbolen tot bepaalde configuraties nogal de nadruk heeft gekregen. In dit soort talen kan men immers zelf bepalen welke uitdrukkingen men als welgevormd wil beschouwen en welke men wil uitsluiten als uitdrukking van de taal in kwestie. Men construeert daartoe een systeem van regels, een calculus, die exact bepaalt welke uitdrukkingen formeel welgevormd zijn. De regels van de calculus opereren slechts op de vorm van de gebruikte en toegelaten tekens en uitdrukkingen. Het begrip ‘welgevormdheid’ is dan ook een zuiver syntaktisch begrip ontstaan in de semiotiek. Het is in dit verband dan ook wenselijk te benadrukken dat de notie ‘grammaticaliteit’ (= welgevormdheid), die Chomsky in de taalkunde op de voorgrond bracht, regelrecht kan worden herleid tot werk uit de jaren dertig en veertig op semiotisch gebied.Ga naar voetnoot1 Daarbij is het zijn kennelijke bedoeling voor natuurlijke talen een zodanige calculus te ontwikkelen dat deze exact de welgevormde uitdrukkingen van een natuurlijke taal kan genereren. Bij natuurlijke talen is er uiteraard geen sprake van een vrije constructie van een calculus, meer van een reconstructie door hypothesevorming met een mogelijkheid tot empirische toetsing. Chomsky past dus geheel in de semiotische traditie van het construeren van grammatica's voor systemen van tekens die bedoeld zijn om over iets te praten. In dit licht kan men ook zien zijn voortdurend benadrukken van de scheiding tussen syntaxis en semantiek.Ga naar voetnoot2 Een calculus bestaat uit minstens de volgende twee componenten: (i) een alfabet waarin de gebruikte tekens worden opgesomd; en (ii) een eindige verzameling formatieregels die vastleggen welke uitdrukkingen (tekens of samenstelsels van tekens) welgevormd zijn in de gegenereerde taal. In de wiskunde en de logica worden calculi geaxiomatiseerd door aan (i) en (ii) de volgende componenten toe te voegen: (iii) een eindige verzameling axiomata, d.w.z. uitdrukkingen die als waar worden aangenomen zonder dat geprobeerd wordt hun geldigheid aan te tonen; en (iv) een eindige verzameling transformaties, d.w.z. afleidingsregels die opereren op axiomata en op de resultaten van transformaties.Ga naar voetnoot3 De constructie van een calculus wordt bepaald door de doeleinden die je hebt. Een | |||||||||||||||
[pagina 545]
| |||||||||||||||
algebraïcus zal zijn calculus zo inrichten dat deze geschikt is voor uitspraken over de verzameling van getallen. Een algebra met symbolen die geïnterpreteerd worden als ‘verliefd zijn op’, of ‘grillig’ is weinig zinvol. Maar in principe zou men een algebraïsche calculus kunnen gebruiken om uitspraken te doen over andere verzamelinger. Men dient dan echter een bijbehorende semantiek te ontwerpen. Ik zal nu heel beknopt een voorbeeld geven van een (niet-axiomatische) calculus met een semantiek die geschikt is om een geografische constellatie weer te geven, en daarna met een semantiek die betrekking heeft op een politieke situatie. Daarmee zal dan het begrip ‘interpretatie’ (van de tekens en de uitdrukkingen) voor de doeleinden van dit artikel voldoende worden toegelicht. Stel, we hebben een calculus C met een alfabet bestaande uit de letters a, b, c, en d, alsmede uit de hoofdletters R en S. Nemen we vervolgens aan een regel die stipuleert dat elke hoofdletter moet worden voorafgegaan en gevolgd door slechts één kleine letter. Dan zijn aRb, aSa, bRd, etc. welgevormde uitdrukkingen in C, terwijl Rsa, baS etc. onwelgevormd zijn. Om nu C te interpreteren, moeten we een domein kiezen waarop we de tekens uit C van toepassing laten zijn. Nemen we in beschouwing een verzameling P met de elementen Amsterdam, Haarlem, Zand voort en Halfweg, en we beperken ons daarbij tot de relaties ‘ligt ten oosten van’ en ‘is verder verwijderd van het Noordzeestrand dan’. We stipuleren vervolgens dat de waarde van de letter a Amsterdam is, van b Halfweg, van c Haarlem en van d Zandvoort; de hoofdletter R staat voor ‘ligt ten oosten van’ en de hoofdletter S voor ‘is verder verwijderd van het Noordzeestrand dan’. Onder deze zgn. valuatie is rRc een ware uitspraak, terwijl dRa, aSa, en cRc onware uitspraken zijn. Een bijzondere situatie ontstaat wanneer men wil dat de calculus alleen maar ware uitspraken oplevert. In ons voorbeeld moet C dan worden ingeperkt. Dat kan door de stipulatie dat de eerste letter in een welgevormde uitdrukking ten opzichte van de laatste letter altijd vroeger in het Nederlandse alfabet moet voorkomen. De aldus herziene calculus, zegt C′, telt nu alleen nog maar ware uitspraken. Het begrip ‘interpretatie’ omvat nu verschillende elementen. In ons geval, (a) de verzameling P, (b) de daarin beschouwde relaties, en (c) de valuatie van de kleine letters met waarden uit P. Als we de interpretatie in ons voorbeeld I noemen, dan zegt men dat de uitspraak aRd waar is onder I. Men zegt ook wel dat I een model levert voor C′. We ontdoen C′ nu van zijn interpretatie I en zoeken een andere bijbehorende semantiek. Stel dat we de verzameling Q willen beschouwen, bestaande uit vier naoorlogse premiers van Nederland. Nemen we als waarde voor a Den Uyl, voor b De Jong, voor c Zijlstra, en voor d Drees Sr. We beschouwen in Q de relaties ‘is premier geworden na’, gesymboliseerd door R, en ‘is van een andere politieke partij dan’, gesymboliseerd door S. Noem deze interpretatie (dat wil dus zeggen, keuze van het domein, keuze van de relaties, waardetoekenning) I′. Dan is onder I′ elke uitspraak van C′ waar. Een uitspraak als bRd betekent De Jong is premier geworden na Drees Sr; bSc betekent ‘De Jong is van een andere politieke partij dan Zijlstra’. Ook I′ is een model voor C′.
In de hierboven gegeven voorbeelden is er sprake van een calculus, een interpretatie en | |||||||||||||||
[pagina 546]
| |||||||||||||||
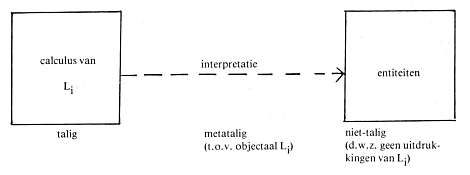
de werkelijkheid waarop de calculus van toepassing is. In Diagram 1 is dit in een eenvoudig schema weergegeven. Naar aanleiding van dit schema zal ik een aantal punten bespreken die van belang zijn.
Diagram 1
Ten eerste, de relatie tussen calculus en interpretatie is die tussen objecttaal en metataal. Dat wil zeggen, de interpretatie van een calculus wordt vastgelegd met behulp van een systeem van regels of stipulaties dat zelf ook deeluitmaakt van een taal. De interpretatietaal is echter principieel onderscheiden van de calculustaal. Zo is de uitspraak aRd een uitspraak van de calculus C′, terwijl de uitspraak (R) (R) aRd is waar onder I dan en dan alleen als Amsterdam ten oosten van Zandvoort ligt behoort tot de metataal voor C′. Ten tweede, de interpretatie legt de relatie vast tussen datgene waarop de calculus van toepassing is en de calculus. De waarden van de gebruikte tekens van een calculus worden gevonden in de werkelijkheid, waarmee hier bedoeld wordt alles wat het geval is geweest, is of zal zijn en alles wat denkbaar is. Bij de constructie van formele talen beperkt men zich tot werkelijkheidsgebieden van bescheiden aard, zoals in de algebra tot de verzameling van getallen. De gebruikelijke term voor het werkelijkheidsgebied dat men op het oog heeft is de term ‘domein’. Het is het gebied waarop de interpretatie betrekking heeft. In de beide voorbeelden waren het de verzamelingen P en Q die de waarden bevatten van de kleine letters uit C′ alsmede de paren tussen welke de relaties R en S gelden. De meest gangbare formele verantwoording van de relatie tussen calculus en werkelijkheid(sgebied) is de verzamelingstheoretische. Hierbij staat de notie ‘functie’ centraal. De valuatie als onderdeel van de interpretatie is een functie van syntaktische elementen naar entiteiten buiten de calculus. Ik kom hierop nog uitvoeriger terug. Ten derde, met één calculus kan men, zoals ik hierboven al heb laten zien, verschillende werkelijkheidsgebieden bestrijken. We zagen dat P en Q extreem kleine en oninteressante verzamelingen zijn. Het was dan ook vrij eenvoudig tot een interpretatie te komen al is de vorming van het CDA voor I′ een complicatie nu Zijlstra en De Jong partijgenoten zijn geworden. Maar de calculus die men hoopt te construeren voor de semantiek van natuurlijke talen dient alle mogelijke werkelijkheidsgebieden te bestrijken. Vandaar ook het streven naar één universeel bruikbare calculus waarmee men alle | |||||||||||||||
[pagina 547]
| |||||||||||||||
domeinen en subdomeinen kan bestrijken. Men kan de predikatenlogica (en als onderdeel daarvan de propositielogica) zien als een poging een geformaliseerde calculus te ontwikkelen. In dit verband moet nadrukkelijk worden gesteld dat een calculus die alleen de ware zinnen van een taal oplevert, vaak niet te vinden is. Zo bestaat er zelfs geen calculus die alle rekenkundige waarheden voortbrengt. Wel is er een calculus ontwikkeld, het predikaatlogisch axiomasysteem, die logische ware zinnen genereert, d.w.z. zinnen die waar zijn in elk model (ofwel, onder elke interpretatie). Het is deze calculus geweest die in de tweede helft van de jaren '60 bij taalkundigen zo sterk in de belangstelling kwam te staan door het werk van generatieve semantici als McCawley. Volgens MCawley hadden logici - ook al construeerden ze calculi voor hun niettaalkundige doeleinden, o.a. voor de precisering van concepten als ‘afleidbaarheid’ en ‘geldigheid’ - bij hun werk toch impliciet een beroep gedaan op hun intuities over de natuurlijke taal. Uitbreiding van hun beperkte axiomasysteem zou volgens hem de basis opleveren van een grammatica. Ten vierde, de noties ‘betekenis’ en ‘waarheid’ zijn zeer nauw met elkaar verbonden. Men kan de interpretatie van een calculus het best zien als een systeem van regels die de waarheidscondities vastleggen van elke zin uit die calculus. In de woorden van Carnap (1968:22): ‘In this way the sentences are interpreted by the rules, i.e. made understandable, because to understand a sentence, to know what is asserted by it, is the same as to know under what conditions it would be true. To formulate it in still another way: the rules determine the meaning or sense of the sentences’ (cursivering van Carnap). Een uitspraak als (R) is een duidelijk voorbeeld van de regels die Carnap hier op het oog heeft. Regels als (R) zijn zo belangrijk omdat ze de gelegenheid bieden tot verificatie door toetsing van gestelde waarheidscondities aan het werkelijkheidsgebied in kwestie. Merk in dit verband ook op dat Seurens hoofdprobleem ‘Hoe komt het dat we zinnen verstaan zoals we ze verstaan?’ in rechtstreeks verband te brengen is met Carnaps notie ‘interpretatie’. Tenslotte, de keuze van de domeinen en de daarop gerichte interpretatie, leidt noodzakelijkerwijs tot een ontologie, d.w.z. tot de vraag welke entiteiten men toestaat als waarden van de geïnterpreteerde elementen van de calculus. Stel dat we bij onze interpretatie I′ van C′ als waarde van d niet Drees Sr maar de aartsengel Gabriël hadden genomen. Dan doet zich direct de vraag voor of Gabriël wel past in een verzameling waartoe Den Uyl, Zijlstra en De Jong behoren. Is Gabriël een mogelijke waarde onder I′? Deze vraag is een vraag naar het bestaan van een entiteit en de daarmee verbonden karakteristieke eigenschappen die in het domein van interpretatie van belang kunnen zijn. Als Gabriël niet bestaat, dan kan het onjuist geacht worden de zin aRd onwaar te noemen. Het begrip ‘waarheid’ is er niet op van toepassing. Het zal ook duidelijk zijn dat de ontologische kwestie in verband staat met waarheidscondities. Sommige mensen zullen er op staan de waarheidscondities empirisch te toetsen. Het is echter beslist lastig een deugdelijk waarheidscriterium te ontwikkelen om het bestaan van Gabriël aan te tonen. | |||||||||||||||
2.2. De lexicografische traditie.Tegenover de betekenisanalyse waarbij een strikt onderscheid geldt tussen een talige syntaxis en een niet-talig domein van interpretatie, staat een type analyse dat o.a. door Quine (1961) werd besproken bij zijn beschouwingen over de synonymie van uitdrukkingen als bachelor en unmarried man. Quine | |||||||||||||||
[pagina 548]
| |||||||||||||||
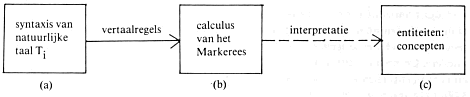
karakteriseert deze linguïstisch-lexicografisch georiënteerde betekenisanalyse als het leggen van een definiërende synonymierelatie tussen definiendum en definiens. Wat er in dit type analyse gebeurt, demonstreert hij in (1a) (1a) bachelor =df unmarried man De vraag die men zich ten aanzien van (1a) moet stellen is de vraag naar de status van unmarried man. Het antwoord luidt natuurlijk: het is een uitdrukking in het Engels net als bachelor zelf. Maar in feite wordt in (1a) het probleem ‘Wat betekent bachelor?’ verschoven naar het definiens waarvan de betekenis zelf ook in het woordenboek staat: bij unmarried en man vindt men de constituerende deelbetekenissen. Er ontstaan bij deze werkwijze situaties waarbij in het woordenboek een woord zowel in het definiendum als in het definiens voorkomt. Hierdoor ontstaat circulariteit. Elke lexicografische benadering moet wel circulair zijn omdat ze binnen de taal blijft. Ze fundeert de semantiek van de taal niet, maar legt de interne semantische organisatie van de taal bloot, en heeft dus een andere (maar ook zeer nuttige) functie dan een semantiek die buiten de taal treedt. Beide benaderingswijzen sluiten elkaar niet principieel uit. Wel is het zo dat de taalkundige semantiek vooral lexicografisch gericht is geweest, terwijl de logische semantiek vooral semiotisch, in termen van Diagram 1, heeft geopereerd. Van beide kanten zijn ook voorzieningen getroffen naar de andere richting. Zo introduceerde Carnap (1964) zgn. betekenispostulaten om de interne semantische organisatie van zijn systeem te expliciteren. Analoog aan (1a) treedt bij hem op een regel als ‘For all x, if x is a bachelor, then x is an unmarried man’. In de semantiek van Katz en Fodor (1964) komt men lemmata tegen die gebaseerd lijken op de lexicografische benadering die hierboven geschetst is. Hun alternatief voor (1a)is(1b): (1b) bachelor; (Animate) (Male) (Unmarried)... De puntkomma geeft hier een synonymierelatie aan tussen bachelor en een verzameling semantische markers. In Katz en Fodor (1964) dat aansloot op het syntaktische model van Chomsky (1957) mag overal waar bachelor voorkomt in de gegenereerde boomstruktuur het lexikale item worden vervangen door de markers. Dit punt nu is voor mijn schets van groot belang, want hier komt een belangrijk gegeven over de ontstaansgeschiedenis van de transformationele semantiek naar voren. Wat er in (1b) gebeurt is weinig anders dan een vertaling op basis van synonymie, althans zo lijkt het in het werk van Katz en Fodor. De markers in (1b) zijn in elk geval talige entiteiten: het zijn elementen van een representatietaal. Maar Katz en Fodor (1964) hebben sterk de indruk gewekt dat definiendum en definiens in (1b) niet wezenlijk van elkaar verschilden in status (Bar-Hillel 1967:546). David Lewis (1972) spreekt in dit verband over een weinigzeggende vertaling van het Engels in het Markerees een taal opgebouwd uit Katziaanse markers. Het rechterdeel van het lemma (1b) is een voorbeeld van een uitdrukking in het Markerees. Voor Lewis is (1b) weinig anders dan een simpele vertaling van een uitdrukking uit het Engels in een kreupel soort pseudo-Engels. Het Markerees is een taal en heeft dus een syntaxis waarvan de regels zijn uit te drukken in een calculus. Een analyse gebaseerd op (1b) leidt dus in feite tot een situatie zoals geschetst in Diagram 2. | |||||||||||||||
[pagina 549]
| |||||||||||||||
Diagram 2
Het bezwaar tegen een analyse als in (1b) is dat niets wordt toegevoegd aan wat men al weet van het woord bachelor. Volgens Lewis is een lemma als (1b) te vergelijken met een vertaling van het Nederlandse woord roos in het Latijnse rosa. Ik zal hieronder proberen duidelijk te maken dat Lewis met zijn kritiek wel een bestaande situatie op het oog had, maar dat deze situatie toch veel ingewikkelder in elkaar zit dan hij voorstelde. Daardoor snijdt zijn kritiek op de taalkunde veel minder hout dan men op het eerste gezicht denkt. Op basis van Katz en Fodor (1964) heeft zich via Katz en Postal (1964) in de tweede helft van de jaren '60 de Katziaanse semantiek verder ontwikkeld, culminerend in het samenvattende werk Katz (1972). Katz heeft zich daarin - overigens zonder erg veel succes - in allerlei bochten gewrongen om de evidente tekortkomingen in de oorspronkelijke formuleringen van zijn theorie te overwinnen. Hij trekt iets in de richting van de semiotiek en als gevolg daarvan is het duidelijk dat een lemma als (1b) bij hem niet zonder meer kan worden beschouwd als een simpele vertaling. In de volgende paragraaf zal dit enigszins verduidelijkt worden. Een andere, overtuigender aanpassing aan de ontwikkelingen in de logische semantiek vindt men in het werk van o.a. Jackendoff (1972; 1976). Ook hierop kom ik nog terug. | |||||||||||||||
2.3. Het Markerees en het Aspects-model.Voor een taalkundige is het niet moeilijk een analyse als in (1b) te verbinden aan een linguïstische traditie op het gebied van de woordsemantiek, de componentiële analyse. Dit type analyse is gebaseerd op het idee dat woordbetekenissen samengesteld zijn uit kleinere eenheden die door onderlinge vergelijking van woorden kunnen worden geïdentificeerd. De meest bekende benamingen voor deze subeenheden zijn: betekeniselementen, features, componenten en markers. Tegenover de componentiële analyse staat de zgn. ongelede analyse. Het verschil tussen beide types analyse is naar mijn mening niet wezenlijk. Markers zoals in (1b) worden verzameld in een lemma voor een bepaald lexikaal item. Maar zoals reeds opgemerkt, kunnen betekenispostulaten het ongelede item in verband brengen met andere items. Lemmata zijn eigenlijk weinig anders dan Carnaps betekenispostulaten (Pollmann en Verkuyl 1976).Ga naar voetnoot4 In de componentiële analyse wordt een woordbetekenis beschouwd als een abstracte entiteit die wordt gepresenteerd als een gestruktureerde verzameling markers. Deze markers nu representeren in de Katziaanse semantiek niet-talige entiteiten, nl. concepten. Daarom heet dit soort semantiek ook wel conceptualistische semantiek. Als | |||||||||||||||
[pagina 550]
| |||||||||||||||
zodanig opponeert deze semantiek wel met de zgn. referentiële semantiek die past in Diagram 1. Globaal gesproken valt deze oppositie samen met het onderscheid tussen de disciplines taalkunde en logica, althans in de jaren '60. In de jaren '30 is er bij Bloomfield bijvoorbeeld sprake van referentiële semantiek, waarbij onder invloed van het zgn. behaviorisme betekenis werd gelijkgesteld met datgene waarnaar wordt verwezen. De representatie van betekeniseenheden vindt plaats met behulp van een taal die hierboven werd aangeduid als het Markerees. Het Markerees heeft een syntaxis: er zijn regels nodig om te bepalen welke markers met andere mogen optreden in welgevormde uitdrukkingen van het Markerees. Bovendien is er sprake van een domein van toepassing, nl. de concepten. Als zodanig zou men dus kunnen zeggen dat het Markerees wel degelijk valt binnen het semiotisch schema in Diagram 1. Met enige goede wil kan men het werk van Katz e.a. ook wel als zodanig opvatten. In het dictionary van Katz en Fodor (1964) liggen de markers opgeslagen: ze behoren tot het alfabet van de Katziaanse calculus. Projectieregels formeren deze markers tot grotere eenheden, die op hun beurt ook weer tot nog grotere eenheden samenklonteren tot het eindresultaat, een zin uit het Markerees, is verkregen. In dit verband kan ook benadrukt worden dat in Katz en Fodor (1964) de selectie beregeld werd in het dictionary. Selectie beperkt in dit geval de syntaxis van het Markerees: vastgesteld wordt dat bepaalde combinaties van markers niet welgevormd zijn in het Markerees. De stelling die ik hier ontwikkel, is dat men de Katziaanse semantiek uit de beginjaren '60 kan zien als een semiotische calculus met een bijbehorende semantiek die past in Diagram 1. Deze stelling berust in eerste instantie op de zoëven genoemde goede wil. Maar er zijn sterker steunpunten te vinden. Immers, men dient te verklaren hoe het komt dat de situatie in de transformationele taalkunde in de jaren '60 niet ten onrechte de indruk wekte te passen in het schema van Diagram 2. Naar mijn mening kan het volgende als een verklaring dienen. Chomsky is zeer goed bekend met semiotisch werk (zie o.a. Chomsky 1975). Zoals al opgemerkt kan zijn opvatting over een syntaxis als een systeem van regels dat bepaalt welke uitdrukkingen welgevormd zijn en welke niet, vrij direct worden herleid tot inzichten in ontwikkelingen in de wiskunde en logica. Zijn Syntactic Structures (1957) kan worden gezien als voorstel, of liever een programma tot het inrichten van een calculus voor het Engels (of andere natuurlijke talen).Ga naar voetnoot5 Chomsky zelf is niet erg geïnteresseerd in semantiek: hij is primair syntakticus. Daardoor concentreert zijn werk zich vooral op het linkerdeel van Diagram 1. In de beginjaren '60 kwamen Katz en Fodor met hun semantische theorie. De fusie met Chomsky vond plaats rond 1964. Chomsky's aandeel was een semantiekloze calculus toegesneden op het Engels, Katz' aandeel was, zoals gezegd een min of meer compleet semiotisch systeem (compleet in de zin van Diagram 1). Het aanknopingspunt was de Chomskyaanse P-marker, de boomstruktuur met lexikale items, woordgroepen en grammatische relaties. Katz' syntaxis was in hoge mate defect: voor de formatie van woordgroepbetekenissen waren zijn projectieregels beslist niet voldoende. Vandaar dat Chomsky's syntaxis te hulp werd geroepen. Dat ging als volgt. Zodra er een syntakti- | |||||||||||||||
[pagina 551]
| |||||||||||||||
sche structuur in Chomsky's calculus werd gegenereerd, werd er als het ware een fotokopie van gemaakt die werd doorgezonden naar de Katziaanse component. Daar kon de syntaktische struktuur gebruikt worden als een verzameling paden waarlangs de betekenissen van onderop naar boven werden geleid. Indien men de eerder al genoemde goede wil laat varen, kan men zeggen dat Katz' systeem parasiteerde op de calculus van Chomsky. Immers, de belangrijkste syntaktische apparatuur van de calculus werd geleend van Chomsky; slechts de projectieregels zijn typerend voor de Markerees-calculus. Door de symbiose van Chomsky en Katz ontstond binnen het transformationele model de situatie zoals geschetst in Diagram 3.
Diagram 3
Het schema in Diagram 3 is o.m. van toepassing op het zgn. Aspects-model. Hierbij is (a) de syntaktische component en (b) de semantische component. Door de relatief zeer grote aandacht voor de inrichting van de syntaktische component bleef men in het algemeen steken bij (b); men kwam nauwelijks toe aan de relatie tussen (b) en (c). Men kan nu ook Lewis' kritiek beter begrijpen: hij richt haar op de preoccupatie met (a) en (b). Aan de andere kant is er toch wel degelijk aandacht besteed aan de relatie tussen (b) en (c). Iemand als Bierwisch is daar een voorbeeld van.Ga naar voetnoot6 Maar zoals gezegd, men concentreerde zich voornamelijk op (a) en (b), met als gevolg dat de indruk gewekt werd dat de transformationele semantiek in de lexicografische traditie van Diagram 2 paste. Ook taalkundigen waren zich in die tijd niet altijd bewust van de feitelijke situatie. Onthullend in dit verband is het gebruik van de term ‘interpretatieve regel’ voor wat in feite vertaalregels zijn. Interpretatie in semiotische zin kan pas plaats vinden bij de overgang van (b) naar (c), maar daar is het in de eerste jaren na Aspects niet van gekomen. De meeste taalkundigen waren bezig met transformaties en met de inrichting van de basiscomponent. Kenmerkend voor de fusieproblemen was dat zowel Chomsky als Katz een eigen opslagplaats hadden. Het dictionary van Katz was semantisch, Chomsky's lexicon was onderdeel van de syntaxis. Rond 1965 had het transformationele model dus twee opslagplaatsen voor lexikale informatie. In later werk zijn lexicon en dictionary min of meer samengesmolten, maar nog in Katz (1972) vindt men sporen van de vroegere scheiding. Katz heeft zich in zijn geschriften nogal opgeworpen als dé representant van de ware transformationele semantiek. Maar als gevolg van de interne controverse bij de | |||||||||||||||
[pagina 552]
| |||||||||||||||
transformationalisten in de periode kort na het verschijnen van Aspects heeft zich een alternatief ontwikkeld in het werk van Jackendoff (1972; 1976) en enkele anderen. Het past in het kader van de zgn. Uitgebreide Standaard Theorie (EST). Ook Jackendoff's positie is in overeenstemming te brengen met het schema in Diagram 3, al zijn er ten aanzien van de relatie tussen (a) en (b) en die tussen (b) en (c) zeer belangrijke verschillen met Katz. Bij Jackendoff is er sprake van een vrij direkte vertaling van syntaktische strukturen uit (a) in uitdrukkingen van een soort predikaatlogische calculus waarin Grubers systeem van thematische relaties is verwerkt. Het lemma van werkwoorden speelt bij deze vertaling een centrale rol omdat de semantische informatie geassocieerd met werkwoorden de vorm krijgt van een zgn. propositionele functie (zie Verkuyl 1976a). De semantische representatie van Jackendoff beoogt mede te verantwoorden wat logici aanduiden als ‘de logische vorm van zinnen’, d.w.z. die struktuur die een taalgebruiker in staat stelt logische gevolgtrekkingen te maken en die hem in staat stelt semantische relaties te leggen tussen zinnen, zoals synonymie, inconsistentie, antonymie, etc. Component (b) is dus bij Jackendoff niet de Markerees-calculus van Katz, al zijn er wel enkele elementen uit terug te vinden (zie bijv. Jackendoff 1976:91; 1972:41, 378). In Diagram 4 is Jackendoffs positie weergegeven.
Diagram 4
Het spreekt vanzelf dat de verhouding tussen (b) en (c) bij Jackendoff anders ligt dan bij Katz. Jackendoff's semantische component maakt een interpretatie in de semiotische zin zeer wel mogelijk, terwijl bij Katz maar niet duidelijk wil worden hoe hij precies het verband ziet tussen het Markerees en het domein van concepten waarop de markers betrekking hebben.Ga naar voetnoot7 | |||||||||||||||
[pagina 553]
| |||||||||||||||
2.4. Referentie, empirisme, extensionalisme en intensionalisme.De semantiek die past binnen het schema van Diagram 1 kan men globaal aanduiden als ‘referentiële semantiek’. Men geeft met die term te kennen dat referentie een belangrijke factor is in de semantische theorie, zo niet de belangrijkste. Een uitdrukking uit een calculus verwijst naar iets buitentaligs (d.w.z. buiten de taal van die calculus) en dit buitentalige zal medebepalend zijn voor wat men ‘betekenis’ noemt. In de praktijk heeft de term ‘referentiële semantiek’ echter een specifiekere inhoud gekregen. Men heeft dan op het oog een empiristisch opgezette semiotische semantiek. En nog specifieker: een semantiek gekenkmerkt door een zeer strenge formele werkwijze, ontwikkeld in de mathematische logica. Een van de grote namen die in dit verband de richting aangeeft is Rudolf Carnap. Het empirisme is hier op te vatten als een kennistheoretische stroming die in de wetenschapsfilosofie een grote invloed heeft gehad, juist door het werk van Carnap in de dertiger en veertiger jaren. Hoezeer Carnaps wetenschapsfilosofie bepalend is geweest voor de semantiek, kan men vinden in een recent overzichtswerk, Koningsveld (1976), waarin heel fraai de parallellie zichtbaar wordt gemaakt tussen de problemen die zich voordoen bij het construeren van een wetenschappelijke theorie en die welke zich voordoen bij het construeren van een semantiek behorend bij een calculus. Het empirisme - althant in zijn strenge vorm - staat zeer afwijzend tegenover het aannemen van abstracte entiteiten in de waarneembare werkelijkheid, zoals eigenschappen, relaties, begripsinhouden, proposities, getallen, etc. Een empiristische ontologie wordt daarom zo eenvoudig mogelijk gehouden. Bestaanskwesties worden daarbij gekoppeld aan het ‘linguistic framework’ dat men hanteert voor het doen van uitspraken over de werkelijkheid. In termen van een calculus houdt dat in dat men met de keuze van de te gebruiken tekens een toegestane uitdrukkingen ontologisch kleur bekent (Carnap spreekt hier van ‘commitment’). Een voorbeeld hiervan is de calculus C′ uit § 2.1 die formeel kon worden uitgewerkt als een predikaatlogisch systeem. Een empiristische semanticus die werkt met regels als (R) zal de relatie ‘ligt ten oosten van’ niet zien als een abstracte entiteit die inhoudelijk kan worden beschreven. Hij struktureert de werkelijkheid a.h.w. door de bril van verzamelingstheoretische noties en als zodanig wordt de genoemde relatie gezien als een verzameling van paren waartussen die relaties geldt. De relatie wordt als het ware weggewerkt naar de leden van de gegeven verzameling plaatsen (Carnap 1964: § 4). Volgens Carnap (1970:73) zijn er twee soorten vragen over het bestaan van dingen: If someone wishes to speak in his language about a new kind of entities, he has to introduce a system of new ways of speaking, subject to new rules; we shall call this procedure the construction of a linguistic framework for the new entities in question. And now we must distinguish two kinds of questions of existence: first, questions of the existence of certain entities of the new kind within the framework; we shall call them internal questions; and second, questions concerning the existence or reality of the system of entities as a whole, called external questions. (Cursivering Carnap) Carnap betoogt nu dat de externe vraag ‘devoid of cognitive content’ is (p. 77) en dat het accepteren van de realiteit van dingen in de werkelijkheid niets meer is dan het accepteren van de regels die de beweringen van de taal constitueren en van regels die deze beweringen testen, accepteren of verwerpen (p. 74). Hij zegt verder: | |||||||||||||||
[pagina 554]
| |||||||||||||||
Generally speaking, if someone accepts a framework for a certain kind of entities, then he is bound to admit the entities as possible designata. Thus the question of the admissibility of entities of a certain type or of abstract entities in general as designata is reduced to the question of the acceptability of the linguistic framework for those entities (p. 81) Als wetenschapsfilosoof was Carnap voornamelijk geïnteresseerd in de constructie van formele wetenschappelijke talen waarin observaties, hypotheses en wetten kunnen worden geformuleerd. Maar wat hij zegt over formele talen gaat natuurlijk ook op voor de predikaatlogische calculus die gebruikt wordt voor de semantische representatie van uitdrukkingen uit de natuurlijke talen. En we zien dan ook dat de grote controverses in de semantiek zich afspelen juist op het punt van de ontologie. Het is op dit punt dat de bekende tegenstelling tussen extensionalisme en intensionalisme aan de orde kan komen. Voor een juist begrip van de kwesties die zich voordoen, wijs ik van tevoren op het volgende: (i) de tegenstelling tussen extensionalisme en intensionalisme valt soms samen met de tegenstelling tussen een empiristisch opgezette semantiek en een niet-empiristisch opgezette semantiek. Als zodanig kan men het werk van empiristen of in de empiristische traditie werkende logici als Carnap, Quine, Lewis, Cresswell en Montague (ondanks hun onderlinge verschillen) stellen tegenover het werk van iemand als Katz, en ook Seuren (Katz en Nagel 1974). (ii) de tegenstelling tussen extensionalisme en intensionalisme valt zeker samen met een tegenstelling tussen empiristen onderling die men zou kunnen aangeven als een controverse tussen preciezen (o.a. Quine en iemand als Nelson Goodman) en rekkelijken (o.a. Cresswell, Lewis, Montague). Deze laatste tegenstelling is verreweg de belangrijkste en ik zal me in dit deel van het artikel er ook toe beperken. Zij speelt zich geheel af binnen het ‘linguistic framework’ van een empiristisch opgezette semantiek. De kernvraag is in hoeverre men concessies mag doen aan het opnemen van abstracte entiteiten in dit framework. Extensionalisten willen de notie ‘betekenis’ laten samenvallen met de notie ‘extensie’ op grond van een beginsel dat inhoudt dat als a = b men het syntaktische element b overal mag substitueren voor a in elke uitdrukking van een calculus. In § 2.5 zal ik dit nader toelichten. Intensionalisten zeggen dat dit beginsel zeker in het geval van natuurlijke talen niet te handhaven is. De extensie van een uitdrukking Ei uit een calculus is datgene waarnaar verwezen wordt door Ei, de referent. De notie ‘referentie’ is echter te algemeen en te vaag. Zo bevat ze bij Strawson (1961) ook aspecten die betrekking hebben op de spreker. De term ‘extensie’ is in de technische, verzamelingstheoretische zin het best op te atten als de functiewaarde van een functie die vaak wordt aangeduid als de valuatie V. Gegeven een uitdrukking Ei uit een calculus, kan men de extensie weergeven als V(Ei). De valuatie V is een functie met als argumentwaarden syntaktische eenheden uit een calculus en als functiewaarden niettalige entiteiten. De aard van deze extensies is nogal afhankelijk van het soort syntaktische categorie waartoe de uitdrukking in kwestie behoort. Meestal onderscheidt men drie extensionele niveau's:(α)verzamelingen, (β) individuen (dingen, elementen), en (γ) waarheidswaarden. Dit laat zich het eenvoudigst illustreren aan de hand van een zin uit de natuurlijke taal (waarvan we de syntaxis nu even zien als een formele calculus). In een zin als: | |||||||||||||||
[pagina 555]
| |||||||||||||||
(2) Jaap zag mijn stoel is de extensie van de soortnaam stoel de verzameling van alle stoelen), de extensie van zien de verzameling van alle paren van individuen X en Y zodanig dat X Y ziet. Op het extensionele niveau (β) is de extensie van mijn stoel mijn stoel (die ik op het oog heb), de extensie van Jaap is Jaap. Het derde niveau is het zinsniveau: de extensie van zin (2) is de waarheidswaarde ‘Waar’ als (2) waar is en de waarheidswaarde ‘Onwaar’ als (2) onwaar is. Het laatste type extensie levert nogal vaak moeilijkheden op voor onze intuïtie: het lijkt natuurlijker als extensie van (2) te nemen het met (2) corresponderende concept. Seuren blijkt er ook moeilijkheden mee te hebben. Aan de andere kant biedt deze benadering de gelegenheid de nadruk te leggen op de voorwaarden die in de werkelijkheid (of een werkelijkheidsgebied) vervuld moeten zijn, wil een zin waar zijn. In het voetspoor van Wittgenstein, Tarski en Carnap kan men menen dat wanneer men een zin begrijpt, men ook weet onder welke voorwaarden deze zin waar is. Het zinsniveau is het meest geschikt om dit aspect te verantwoorden. Daarom offert men gaarne een stukje intuïtie op. In de volgende paragraaf zal ik laten zien hoe intensionalisten er alsnog naar streven om te verantwoorden dat met een zin een bepaalde begripsinhoud correspondeert. De noties ‘extensie’ en ‘intensie’ zijn voor het eerst heel precies in een verzamelingstheoretisch kader gebracht door Carnap (1964). | |||||||||||||||
2.5. Identiteitsbeweringen en ondoorzichtige conteksten; de noodzaak van intensies.Een zuiver extensionalistisch opgezette semantiek impliceert dat men de notie ‘betekenis’ wil wegwerken ten gunste van de notie ‘extensie’. Een zeer simpel voorbeeld van een zuiver extensionalistisch opgezette calculus is de algebra. Stel, je hebt een uitdrukking in een algebraïsche calculus, zeg a + b = c en het is ook het geval dat b = e + f. Dan moet het krachtens een wet die geldt voor elke extensionalistische semantiek, mogelijk zijn de uitdrukking e + f te substitueren voor b in elke uitspraak waarin b optreedt. Dat wil zeggen, gegeven de waarheid van b = e + f geldt: (3) a + b = c ⇔ a + e + f = c waarbij ‘⇔’ staat voor de relatie ‘is logisch equivalent met’. Men doet. hierbij buiten de algebra om een beroep op een universeel geldende afspraak die vastlegt wat men onder ‘=’ verstaat. Het symbool b staat voor een bepaalde getalswaarde en als deze identiek is met de som van twee andere waarden dan is substitutie onder behoud van de waarheidswaarde van a + b = c toegestaan. In de algebra is kennelijk geen interesse voor de vorm van de gebruikte tekens wat betreft hun interpretatie. Wel uiteraard onder het oogpunt van syntaktische operaties als optellen, aftrekken, etc. Bekende voorbeelden van substitutie zijn gevallen als 42 + 162 = 16 + 256 = 272. Belangrijk hierbij is dat de waarheidswaarde als verankeringspunt wordt aangehouden. Stel dat a + b in ons voorbeeld staat voor 6 + 8, c voor 15, en e + f voor 3 + 5, dan is a + b = c onwaar. Dan moet ook als logisch gevolg van (3) het rechtergedeelte a + e + f = c ook onwaar zijn. Het is echter duidelijk dat de vorm van de symbolen, behalve bij syntaktische operaties, ook een andere rol kan spelen voor de gebruiker van de calculus. Het hangt uiteraard af van zijn doeleinden. Een wiskundeleraar kan opgelucht over tenminste enig besef van wiskundig inzicht zin (4) gebruiken en met enig verwijt over dezelfde persoon (5): | |||||||||||||||
[pagina 556]
| |||||||||||||||
(4) Piet gelooft dat 162 = 162 Beide zinnen kunnen waar zijn. Piet kan namelijk slecht zijn in rekenen en toch geloven dat hij goed gerekend heeft in het geval van (5), terwijl hij geen enkele moeite heeft met de logische wet a = a. Substitueerbaarheid heeft kennelijk haar grenzen. Algebraïci houden zinnen als (4) en (5) natuurlijk buiten hun calculus. Zij streven naar een zuiver extensionalistische opzet. Hun interpretatiedomein is dan ook relatief eenvoudig: alleen getalswaarden zijn van belang. Door het werk van Frege is men zich er echter van bewust geworden dat een zuiver extensionalistische benadering toch al snel tot moeilijkheden leidt. Vergelijk bijvoorbeeld: (4') 162 = 162 Uitspraak (4') is een voorbeeld van een logische wet. Het is een identiteitsbewering van de vorm a = a. Uitspraak (5') heeft een andere status ondanks het gebruik van het symbool ‘=’. Kennelijk is er een soort ‘meerwaarde’ aanwezig in de vorm van de uitspraken, die overblijft als men de onderlinge substitueerbaarheid verdisconteert. Dat wil zeggen, de vorm ‘162’ en de vorm ‘256’ hebben iets dat niet meedoet met de substitutie. In de algebra lost men het verschil tussen (4') en (5') op door een onderscheid aan te brengen tussen verschillende soorten ‘=’. In zin (4') is sprake van een echte identiteitsbewering, in (5') gaat het om een operatie. Frege demonstreerde het probleem van de identiteitsbeweringen met voorbeelden uit de natuurlijke taal die inmiddels klassiek zijn geworden. Vergelijk: (6) De Avondster is de Avondster Het probleem is: als zin (7) waar is dan mag de Morgenster in elke zin van het Nederlands vervangen worden door de Avondster. Doet men dat dan ook in (7) dan is het resultaat zin (6). Maar beide zinnen hebben een geheel andere status. Zin (6) is net als (4') een voorbeeld van een logische wet, terwijl (7) net als (5') nieuwe informatie kan geven. De conclusie is dat er ‘iets’ in de vorm van de gesubstitueerde symbolen moet zitten dat niet meedoet met de substitutie. Dit ‘iets’ heet bij Frege ‘Sinn’. Zou men het niet verantwoorden dan zou (7) een uitspraak a priori zijn en daarmee nooit gebruikt kunnen worden om iemand te leren dat de Avondster dezelfde planeet is als de Morgenster. Tegenwoordig wordt Frege's ‘Sinn’ meestal ‘intensie’ genoemd. Net als bij ‘extensie’ geldt dat men ook hier het best deze term kan opvatten als een technische, verzamelingstheoretische term, zoals gebruikt in het werk van o.a. Carnap (1964), Lewis (1972), Montague (1973). Zie in dit verband ook Verkuyl (1974). Het extensionaliteitsaxioma dat substitueerbaarheid garandeert bij identiteit van extensies, leidt zoals gezegd tot moeilijkheden in gevallen als (4) en (5). Men spreekt dan meestal van zgn. opake of ondoorzichtige conteksten. De identiteitsbewering is hier ingebed in het complement van een werkwoord. Werkwoorden als geloven hebben de eigenschap de substitueerbaarheid te blokkeren. Het ‘geloof-systeem’ van de spreker en dat van het subject van geloven kunnen verschillen. Quine's voorbeelden in dit verband zijn Tom believes that Cicero denounced Catiline en Tom believes that | |||||||||||||||
[pagina 557]
| |||||||||||||||
Tully denounced Catiline. Als Tom niet weet dat Cicero en Tullius een en dezelfde persoon zijn kan de ene zin waar zijn en de andere onwaar (Quine 1960; 1961). Ook modale uitdrukkingen kunnen moeilijkheden opleveren bij de substitueerbaarheid onder identiteit. Een bekend voorbeeld is hier: (8) a. 9 is noodzakelijk groter dan 7. Zin (8c) volgt niet logisch uit de twee premissen. Dit is toe te schrijven aan de aanwezigheid van noodzakelijk in (8a) en (8c). Ook hier spreekt men van ondoorzichtige conteksten. Modale operatoren hebben net als werkwoorden van het type geloven de eigenschap dat ze een bepaald bereik hebben binnen welk gebied de substitueerbaarheid niet goed mogelijk is. Mede als gevolg van de discussie over de moeilijkheden bij substitueerbaarheid is in de laatste twintig jaar een ontwikkeling op gang gekomen die geleid heeft tot het ontstaan van de zgn. intensionele logica. Men kan deze logica in het algemeen omschrijven als die uitbreiding van de klassieke formele logica die intensies hanteert als functies van zgn. indices naar extensies (d.w.z. klassen, individuen en waarheidswaarden). Een index is een n-tupel van contekstuele factoren die het taalgebruik mede bepalen. Lewis (1972) representeert een index als een reeks coördinaten. Deze coördinaten verantwoorden steeds wisselende contekstuele kenmerken die mede bepalend zijn voor de extensies. Zo is er een sprekerscoördinaat in verband met zinnen als Ik ben ziek, een tijdscoördinaat in verband met zinnen als Vandaag is het Woensdag, een plaatscoördinaat, en nog enkele, waaronder een mogelijke werelden-coördinaat in verband met modale uitdrukkingen. De recente opbloei van de modale logica is te danken aan Kripke's formele precisering van de vrijwel vergeten Leibniziaanse notie ‘mogelijke wereld’. Zeer kort samengevat is hiermee bedoeld een situatie of stand van zaken. De waarheid van uitspraken wordt nu gerelativeerd met betrekking tot dergelijke standen van zaken. Iets is noodzakelijk waar als het waar is in alle denkbare en werkelijke standen van zaken en voor alle tijden. Contingente waarheden gelden voor enkele werelden en tijdstippen. Een zin als Den Uyl is oppositieleider was waar in de periode vlak voor 1973 en onwaar in de periode 1973-mei 1977. Men kan nu zeggen dat de notie ‘intensie’ ten opzichte van de notie ‘extensie’ een enorme verruiming inhoudt. Een voorbeeld kan hier verduidelijkend werken. De extensie van de uitdrukking de huidige wereldkampioen schaken is op dit ogenblik de Russische schaker Karpov. De intensie van de huidige wereldkampioen schaken is een zgn. individueel concept dat beschouwd dient te worden als een functie die op basis van een aantal gegevens uit de verzameling van index-coördinaten de gewenste extensie oplevert. Daarmee wordt het volgende bedoeld (en hierbij beperk ik me nu even tot de mogelijke-werelden-coördinaat en de tijdscoördinaat). Stel dat I de verzameling is van alle werelden en J de verzameling van alle tijdstippen. Dan kan men zeggen dat de wereldkampioen anno 1950 met die twee verzamelingen in verband te brengen is: de wereld van toen en die periode behoren tot resp. I en J. Bij een individueel concept worden I en J als het ware opengehouden. Met andere woorden, de reële ‘looptijd’ van het intensionele object is in feite begonnen op het moment dat de eerste wereld-kampioen schaken werd uitgeroepen. (Men kan het concept evenwel uitbreiden naar | |||||||||||||||
[pagina 558]
| |||||||||||||||
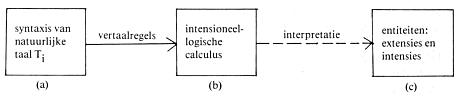
het verleden en naar de toekomst.) Het belangrijke punt is dat men bij vervanging van de variabelen voor werelden en tijden door de geëigende waarden, direct terechtkomt bij de juiste extensie. Neemt men als waarden de stand van zaken in 1950 dan is de extensie van het intensionele object ‘de huidige wereldkampioen schaken’ Botwinnik. Neemt men als waarden de stand van zaken in 1936 dan is de extensie Euwe. De intensie is dus te zien als een generalisatie over alle mogelijke extensies van een uitdrukking. Het grote voordeel van deze generalisatie is dat men nu de mogelijkheid heeft problemen als die in (6) en (7) op te lossen. Verschillende intensionele objecten kunnen immers dezelfde extensie hebben. De index corresponderend met de Avondster ziet er anders uit dan die welke correspondeert met de Morgenster. Maar in beide gevallen is er sprake van dezelfde extensie. De intensionele logica heeft een duidelijke empiristische achtergrond en herkomst. Vandaar de zeer nauwe relatie tussen extensie en intensie. Dat wil zeggen gegeven intensies komt men altijd bij extensies uit en deze extensies kunnen worden gedetermineerd in termen van waarheidscondities. De extensie blijft als het ware de spil waar alles om draait: de valuatie V voert van syntactische categorie naar de corresponderende extensie op een van de drie extensionele niveau's. Tegelijkertijd bepalen wereld, tijd, plaats, en andere factoren welke extensie zich voordoet als manifestatie van het corresponderende intensionele object. In de zgn. Montaguegrammatica is een intensionele logica opgenomen als een der componenten, dit in verband met de bekende problemen betreffende de substitueerbaarheid onder identiteit. Het is beslist niet doenlijk in dit korte bestek in te gaan op de technische beschrijving van een Montaguegrammatica. Hiervoor zij verwezen naar Partee (1975). Voldoende is in dit verband te wijzen op het feit dat een Montaguegrammatica in zijn standaardvorm past in Diagram 5.
Diagram 5
De syntaxis van Montague is verwant aan de zgn. categoriale grammatica's. Deze verschillen van de Chomsky-syntaxis o.m. daarin dat het lexicon als uitgangspunt wordt genomen. Lexikale items worden gespecificeerd wat betreft hun mogelijkheden van optreden met andere categorieën zodanig dat ze samen een nieuwe hogere categorie vormen. De grammatica bevat regels die vastleggen met welke andere categorieën dergelijke eenheden kunnen worden gevormd, tot de hoogste S is bereikt. Een categoriale grammatica werkt - in termen van een boomstruktuur - als het ware van onderen naar boven. Aangetoond is overigens dat Chomsky's syntaxis en Montague's syntaxis in zwak generatieve capaciteit equivalent zijn: ze genereren dezelfde zinnen van de natuurlijke taal. Vertaalregels vormen de uitdrukkingen van Li om in uitdrukkingen van de intensionele logica. Montague is hier erg explicicet. Trouwens zijn hele systeem is van een | |||||||||||||||
[pagina 559]
| |||||||||||||||
onovertroffen rigoureuze preciesheid. Uitdrukkingen uit de intensionele calculus (b) worden tenslotte geïnterpreteerd in de bekende semiotische zin van het woord: (b) en (c) corresponderen met Diagram 1. Opmerkelijk is nu dat de positie van de transformationele grammatica en die van de Montaguegrammatica wat betreft de relatie tussen taal en datgene waarover met behulp van die taal gesproken wordt, niet zoveel verschillen; althans, hoeven te verschillen. Zowel in Diagram 4 als in Diagram 5 is sprake van zowel vertaalregels die de relatie tussen (a) en (b) leggen, als interpretatieregels die de relatie tussen (b) en (c) bepalen. Vooral in de laatste jaren is er enige convergentie te bespeuren tussen beide richtingen. | |||||||||||||||
2.6. Empirisme, rationalisme, mentalisme, fysicalisme en idealisme.Een laatste punt dat in deze paragraaf enige aandacht vraagt is de kennistheoretische en ontologische status van de entiteiten waarnaar verwezen wordt door een calculus. Zoals opgemerkt is het technische middel in een empiristische opgezette semantiek de verzamelings-theoretische notie ‘functie’. Bij de vraag hoe de toegelaten entiteiten perceptueel en cognitief door de waarnemende en denkende taalgebruiker worden verwerkt en hoe dit in een algemene theorie over taal moet worden verantwoord, belandt men midden in een eeuwenoude filosofische discussie over de relatie tussen zintuiglijke gegevens en het daarop opererende cognitieve systeem enerzijds en de werkelijkheid anderzijds. Deze discussie heeft kennistheoretische aspecten en ontologische aspecten die niet altijd uit elkaar worden gehouden. Chomsky (o.a. 1974) stelt dat het taalverwervende kind bij de opbouw van zijn grammatica gebruik maakt van en gestuurd wordt door zeer restrictieve principes van het cognitieve systeem waarmee het ter wereld is gekomen. Deze principes werken universeel en kunnen worden toegeschreven aan biologische eigenschappen van de menselijke soort. Syntaktisch onderzoek naar de menselijke taal is volgens Chomsky een belangrijk (zo niet het belangrijkste) middel tot inzicht in de struktuur van dit cognitieve systeem. Het benadrukken van de hoge organisatiegraad van onze cognitie, maar vooral van de gedachte dat dit systeem al in grote trekken is gevormd bij de geboorte en dat het na een relatief geringe stimulering als zelfstandig informatieverwerkend systeem opereert, brengt Chomsky binnen een opvatting die hijzelf zowel rationalistisch als mentalistisch heeft genoemd in de loop van zijn werk. Op dit punt doet zich een grote verwarring voor. Een empirist als Quine is er volledig van overtuigd dat de mens bij zijn geboorte de beschikking heeft over complexe aangeboren mentale mechanismes. Quine verstaat onder empirisme ‘just the insistence upon couching all criteria in observation terms. By observation terms I mean terms that are or can be taught by ostension, and whose application in each particular case can therefore be checked intersubjectively’ (Quine 1976:58; zie echter ook Chomsky 1974: 200 vv). Quine benadrukt hier het punt dat alle kennis die wij hebben omtrent de werkelijkheid direct of indirect afhankelijk is van onze zintuigen. Een dergelijk standpunt hecht uiteraard veel waarde aan criteria ter beoordeling van uitspraken van het type (R) waarin waarheidscondities ten aanzien van bepaalde uitdrukkingen uit een calculus worden vastgelegd. Het feit dat de geest als regulerend mechanisme de waarneming van entiteiten kan | |||||||||||||||
[pagina 560]
| |||||||||||||||
beïnvloeden, heeft binnen het empirisme geleid tot een tegenstelling op het ontologische vlak die men zou kunnen karakteriseren als een oppositie tussen mentalisme en fysicalisme. Ik zal proberen met een voorbeeld duidelijk te maken waar het in het verband van dit artikel om gaat. Stel, we hebben als betekeniselement van het woord tomaat een element ROOD aangenomen dat als uitdrukking dienst doet in een calculus van het type (b) uit diagram 4. Dan is de vraag wat wordt uitgedrukt door ROOD. Carnap (1966:20) schetst heel duidelijk de tegenstelling die hier aan de orde is: ..., the properties of things are not meant as something mental, say images or sense-data, but as something physical that the things have, a side or aspect or component or character of the things. If an observer sees that this table is red, then the table has the character Red and the observer has the corresponding character Red-Seeing. By the property Red we mean the first, not the second; we mean that physical character of the thing which the physicist explains as a certain disposition to selective reflection, not that psychological character of the observer which the physiologist explains as a certain disposition to a specific reaction by the sensory part of the nervous system. Men dient dit citaat te zien als een onderdeel van een zeer uitvoerige discussie tussen empiristen onderling over de relatie tussen ‘the world of physics’ en ‘the world of sense’ (Russell o.a. 1969; 1970). Het strenge fysicalistische standpunt van iemand als Carnap is zeker te begrijpen als reactie op het Duitse idealisme waar de subjectivering van het wereldbeeld nogal griezelige vormen had aangenomen. Carnap verdedigt de opvatting dat (c) in Diagram 4 en 5 direct in verband dient te worden gebracht met ‘something objective that is found in nature’ (1966:21). Als zodanig vertegenwoordigt Carnap een heel strenge vorm van het logisch empirisme die op dit ogenblik overigens niet meer en vogue is, ook niet bij empiristen. Allerlei ontwikkelingen in de psychologische functieleer hebben geleid tot een afzwakking van het strenge fysicalisme. Russells opvatting brengt (c) in Diagram en 5 meer in verband met het cognitieve systeem van de taalgebruiker en probeert van daar uit de relatie tot de fysische wereld te specificeren. Men kan deze opvatting met recht mentalistisch noemen. Wie dan ook een mentalistische opvatting zonder meer stelt tegenover een empiristische opvatting, wekt verwarring doordat niet duidelijk wordt waar de anti-empiristische kritiek eigenlijk betrekking op heeft. Wie zich zonder meer bekent tot een mentalistische semantische theorie, loopt gevaar terecht te komen in de valkuilen van een vaag idealisme dat stelt ‘whatever exists, or at any rate whatever can be known to exist, must be in some sense mental’ (zie Russell 1970: 19 vv). Het gaat in deze kwestie dus om drie groeperingen: fysicalisten à la Carnap (1966), mentalistische empiristen zoals Russell, en buiten het empirisme opererende mentalisten. Seuren behoort tot deze laatste groep. Zoals gezegd is Chomsky's positie niet zo duidelijk. Hij noemt zijn aanname van een complex, aangeboren mentaal mechanisme rationalistisch, en als zodanig plaatst hij zich buiten het empiristisch kader. Maar het is heel goed mogelijk dat hij met zijn ontologie behoort tot de vierde, nog niet genoemde groepering, de fysicalisten (ook wel realisten genoemd) die niet-empiristisch zijn. Meningsverschillen worden vaak pas interessant als de betreffende oppositie zo scherp mogelijk wordt gesteld. Zo ook hier. Al heeft men extreme vertegenwoordigers, de praktijk is dat men behoorlijk veel water in de wijn vindt. Zo hebben we gezien dat intensionele objecten hun intrede doen in een overwegend empiristisch kader (Monta- | |||||||||||||||
[pagina 561]
| |||||||||||||||
gue is overigens nogal neutraal ten aanzien van ontologische kwesties). Wel is het zo dat men daarbij als veiligheidsmaatregel deze abstracte objecten altijd verbindt met extensies, zodat er altijd controleerbaarheid mogelijk is in termen van intersubjectieve waarheidscriteria: de entiteiten zijn altijd te localiseren met behulp van een temporeel en spatieel coördinatenstelsel in het domein van de interpretatie. Een mentalisering van een calculus van het type (b) in Diagram 4 en 5 houdt onder meer in dat men noties als ‘domein van interpretatie’, ‘waarheid’, ‘bereik van variabelen’, etc. enigszins subjectiveert. Dit ‘enigszins’ geeft de mate aan waarin men ten opzichte van het fysicalistische standpunt in de richting van de mentalistische opvatting gaat. Bij mentalisering is bijv. het domein van de interpretatie van uitdrukkingen uit de calculus niet langer een in de fysische werkelijkheid te lokaliseren werkelijkheidsgebied waar de dingen an sich zijn, maar een in de menselijke geest aanwezige cognitieve ruimte waarin de entiteiten die men in (c) van Diagram 4 en 5 toelaat, voorkomen. Een zeer interessante hypothese over zo'n cognitieve ruimte wordt ontwikkeld in Clark (1973). Zijn notie ‘perceptuele ruimte’ heeft betrekking op de cognitieve organisatie die ten grondslag ligt aan onze interne (mentale) representatie van perceptuele ervaringen die we hebben met ruimte en tijd. Zij heeft de vorm van een coördinatenstelsel met punten, lijnen en vlakken die als referentiemogelijkheid dienst doen en met richtingen. Het is betrekkelijk eenvoudig Jackendoffs systeem van semantische representaties, d.w.z. zijn predikaatlogische calculus, te laten opereren in termen van dergelijke cognitieve ruimten (zie Verkuyl 1967b). In het algemeen kan men in de psycholinguistische literatuur waarnemen dat enige beïnvloeding van Chomskyaanse zijde op dit punt heeft plaatsgevonden: de aanname van een complex cognitief systeem waarvan hef taalvermogen deel uitmaakt, heeft als natuurlijke consequentie het inzicht dat dit systeem relatief autonoom dient te zijn ten opzichte van informatie uit de waarneembare werkelijkheid. De empiristische soep wordt kennelijk niet zo heet gegeven als zii ten tijde van Carnap werd opgediend.
Utrecht, Instituut De Vooy h.j. verkuyl |
|