De Vraagbaak. Almanak voor Suriname 1928



[pagina 28]
Formules voor het berekenen van den inhoud. Der meest voorkomende vlakken (O) en lichamen (I) Vierkant of Quadraat. O = a², waarin a de zijde.
Rechthoek. O = a x b, waarin a en b de zijden.
Parallelogram. O = a x h, waarin a basis en h de hoogte.
Driehoek.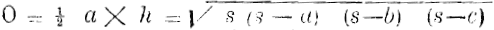 , waarin h de hoogte, s = ½ (a + b + c en a, b en c de zijden.
Trapezium. O = (a + b) x h/s waarin a en b de evenwijdige zijden en h de loodrechte afstand tusschen de evenwijdige zijden
Cirkel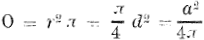 waarin r de straal, d de dia meter, a de omtrek en π = 3.14(15927).
Cirkelsegment (bij benadering)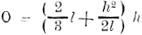 , waarin l de koorde en h de pijl.
Eclips. O = a b π, waarin a de helft der korte en b de helft der lange as.

[pagina 29]
Parabool. O = ⅔g h, waarin g eene koorde loodrecht op de as en h het door die koorde afgesneden stuk der as.
Kubus of Teerling. I = a³, waarin a de zijde.
Prisma en Cylinder. I = O x h, waarin O het grondvlak en h de hoogte,
Piramide en Kegel. I = ⅓ O x h (Als boven),
Afgeknotte Piramide en Kegel.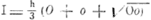 , waarin O het grondvlak, o het bovenvlak, en h de loodrechte afstand tusschen beide vlakken.
Bol. O = 4π r², I = 4/3 π r³, waarin r de straal, π = 3.14 (15927)
Inhoud van een vat. a, Wanneer de hoepels, cirkelvormig gebogen zijn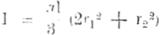 b, Wanneer ze parabolisch gebogen zijn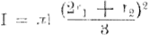 I = binnenlengte v.h. vat; r₁ = binnenstraal bij het spongat; r₂ = binnenstraal a/b boven en benedenkant v/h vat.