Spiegel der Letteren. Jaargang 7

[p. 161]

[Nummer 3]

Schaken met De Castelein

I

Alle poëzie is onnatuurlijk taalgebruik. De kans dat de volzinnen in een krant zich vanzelf ordenen tot vijfvoetige jamben is één op het miljard, heel de verheven inhoud ten spijt. De terugkeer van dezelfde klankgroep na telkens tien lettergrepen is even waarschijnlijk als een struik met altijd één decimeter tussen roos en roos. De hoeveelheid menselijke mededelingen die juist voltooid zijn na veertien volle regels, geen woord meer, geen syllabe minder, valt in het niet bij de bergen sonnetten uit de wereldliteratuur. Er is geen kunst zonder kunnen, er is geen poëzie dan krachtens de moeilijkheden die een dichter zich oplegt. In het overwinnen daarvan ligt driekwart van zijn talent, en in het schijnbaar moeiteloos overwonnen-zijn driekwart van de bekoring voor anderen. Die moeilijkheden zijn niet eeuwig en overal dezelfde, van tijd tot tijd noch van taal tot taal. De rederijker had zijn eigen spelregels, ánders dan de middeleeuwer, de gouden-eeuwer, de Tachtiger of de Vijftiger. Nog onnatuurlijker misschien, maar wie waagt zich aan die beslissing? Wij zijn immers niet enkel toeschouwer, ook deelgenoot. Gewoonte heeft een schijn van natuurlijkheid die het voorschrift mist. Maar wat als voorschrift begon, kan gewoonte wórden. En voorbije gewoonte, eenmaal geformuleerd, doet lateren vaak als voorschrift aan. Hebben de rederijkers elkaar en zichzelf echt zoveel voorgeschreven? Rondeel, ballade, refrein en lied zijn eigenlijk vrij eenvoudig. Pas als Matthijs de Castelein zich tegen het slot van zijn ‘Const’ nog bondig bezighoudt met dobbelsteerten, ketendichten, ricqueracken en baguenauden, wordt de zaak ingewikkeld. Maar dan gaat ook deze meester een zeker voorbehoud tonen, al geeft hij meteen zelf een voorbeeld van onnatuurlijk taalgebruik in het kwadraat: zijn schaakbord.

In de eerste druk van De Const van Rhetoriken¹, postuum verschenen: ‘Te Ghendt. / By Ian Cauweel, thaluer dōderstrate in de

1 Ik mocht gebruik maken van het fraaie exemplaar uit de Stadsbibliotheek van Haarlem.

[p. 162]

Cau-/we, oft op den houck vander hooghpoort / neuē dē Iinghele. An̅o. M.D.LV.’, is dit schaakbord als eenzijdig bedrukt, uitvouwbaar blad, gemerkt P, opgenomen tussen, pagina 224 en 225, dus na vel 14, gemerkt O, en vóór vel 15, gemerkt Q. Behalve deze duidelijke aanwijzing voor de binder, staat bovendien onderaan blz. 224 nog in cursief: ‘Hier volghd het Schaeckberd.’ Al heeft de druktechniek deze plaatsing stellig mede bepaald, er is geen ernstige onregelmatigheid ontstaan; dat bewijst de inleiding tot de Rethorike extraordinaire, die als een soort inhoudsopgave op rijm te vinden is in de balladen 216 en 217, op blz. 221:

Hier zuldy gaen lesen dan vry zōder swichtē,
Om aerbeids verlichten, of God maeghd beletten,
Intricate baladen, die menighen ontstichten,
Dobbel steerten, ende Keten dichten,
Vremde Sneden, Scaeckberd, vry van smetten,
Veersen in dichte, Simpletten, Dobbletten,
Ricqueracken, Baguenauden, als qua iuweelen,
Met twee stocken, al dichten hart om setten,
Limen, of Deffianchen, ende Aude Rondeelen.

Dbeghin ende hende van zomighen spelen,
Benedicite, zal ick quelen, metter Gratien.
Superflue dicht, en sal u niet veruelen,
Parabolen, Cocorullen en magh ick niet helen,
Moralen, Regheldicht, noch Comparatien.
Endel-veers, Spraken, ende Interrogatien,
Epitaphien, Prouerbien ick verclare,
Gheraedsels, ende Eed der rethorijcscher natien
Ende dit heete ic Rethorike extraordinare.

Na deze didaktische tekst volgen inderdaad als voorbeelden op de blz. 222-224: ‘Sesse baladen, in eene; Balade intricaet; Ander Balade intricaet, sterckere dan de voorgaende; Dobbel steerten; Kéten-dicht; Ander vremde Snede’; deze laatste benaming staat ook nog op de blz. 225-226. Dáár had het schaakbord dus moeten staan; het is uit hoofde van de bindtechniek precies anderhalve bladzijde te vroeg geplaatst. Verderop echter, nadat De Castelein nog een kleine veertig voorbeelden van andere dichtvormen gegeven heeft, komt hij in ballade 223 (blz. 241) nog even op het schaakbord terug om zijn kunstgenoten te waarschuwen voor de grootste moeilijkheid ervan:

[p. 163]

 

Nopende tSchaeckberd dat vueren staet,

 

Vvild ghy tsghelijcks maken om dijns zins verlichten

 

Beghind an tcruce eerst dats minen raet:

 

Vvant daer af dependéren alle dander dichten.

Er is in deze teksten weinig belangrijks en in het geheel niets, dat een verklaring inhoudt voor de vreemde aanduiding boven het bord: ‘Honderd achte’. Men heeft gemeend dat het wees op het aantal lettergrepen van een kolom horizontaal plus een baan verticaal². Maar ten eerste is er dan het feit dat het niet klopt: bij staand rijm zijn er per vakje zes lettergrepen, bij slepend rijm zeven; het getal 108 kan enkel ontstaan uit vier regels met staand rijm en twaalf regels met slepend rijm, een verhouding van één tegen drie. Op het gehele bord zouden er dan 16 vakjes met staand en 48 met slepend rijm moeten zijn, maar in werkelijkheid zijn het er 24 en 40. Ten tweede wordt er in rederijkerstheorieën enkel gesproken over het aantal syllaben per versregel, en over het aantal versregels per gedicht. En ten derde betreft het hier niet eens één gedicht, maar twee tezamen. Waarom eigenlijk, en waarom maar twee? Is er een ander voorbeeld te vinden, dat rederijkers het aantal syllaben van een tekst opgeven, of van een paar teksten bijeen? Zo lang dat ontbreekt, is een verklaring van deze aard zinledig, nog afgezien van de constatering dat ze in dit geval niet klopt met de feiten. De mening dat de fout dan in de feiten zit, is een al te goedkope uitweg³. Verschillende andere pogingen echter leveren evenmin een bruikbaar resultaat op: noch bij bladzijde 108, noch bij ballade 108 is enige aansluiting te vinden of te forceren, tenzij men z'n heil zoekt in de toepasselijke slotregel hiervan:

Hy es den besten dichtere die best stellen can.

Maar het nummer kan De Castelein niet bekend zijn geweest: blijkens de ‘VVaerschvwijnghe tot den Lezer’ (blz. 252) werd het door de uitgever toegevoegd. Om diezelfde reden zal men ook met ballade 216, toevallig tweemaal 108, niets kunnen beginnen; het zou bovendien ballade 217 moeten zijn daar men zich bij 190 in de telling heeft ver-

2 Zowel de Bibliotheca Belgica, C. 154, (Gand-La Haye 1880-1890) beweert dit, alsook J. van Leeuwen in zijn proefschrift: Matthijs de Castelein (Utrecht 1894; blz. 113.)

3 Aldus Van Leeuwen: ‘In ieder geval is het Schaeckberd niet geheel in den haak, en heeft de Castelein de eischen van het schaakbord blijkbaar opgeofferd aan die der ballade.’ (Diss. blz. 113)

[p. 164]

gist. Het schaakbord is ook niet het 108ste van de reeks voorbeelden die van ballade 162 af de Const onderbreken en toelichten: het staat op of nabij de 80, op een totaal van 116. Is het dan soms een aanduiding geweest, door De Castelein met geheel andere bedoeling aangebracht op het handschrift waar de ‘VVaerschvwijnghe’ het over heeft, en ten onrechte gedrukt? Als het alleen maar 108 betekent, waarom staat het er dan niet in cijfers? Maar als het in letters op het manuscript heeft gestaan, hééft het er dan wel gestaan? Misschien moeten we met onze veronderstellingen een heel andere kant op. Kan het geen toespeling zijn op de acht maal acht vakjes, en tegelijk een woordspeling in de trant van: Geef acht, of: Neemt u in acht? Maar wát dan met die honderd? Mag men menen dat men voor het goed oplossen van het schaakraadsel niet slechts veel of zeer veel, maar honderdvoud acht moet slaan op de spelregels? Is dat taalkundig onmogelijk? Maar is bij taalspel ooit iéts onmogelijk? Of heeft er, overeenkomstig de opmerkelijke plaatsing, een soort spreuk gestaan, als titel of als motto, zoiets als ‘Houd ende achte’ of ‘Houd u in achte’, dat door verkeerd lezen gedegradeerd is tot een getal⁴? Kan zelfs de meest-nabije uitwijkvorm: ‘Houdend achte’ geen fraaie veelvoudige woordspeling zijn: ‘het achttal bevattende’, dus gebaseerd op het getal acht, en tegelijk: ‘gedurig acht gevende’, en dit laatste weer tweeledig bedoeld, zowel op de dichterlijke spélregels als op de zedelijke lééfregels, waarmee dan tevens weer de inhoud wordt samengevat van het gehele complex balladen? En past dit niet voortreffelijk bij de man die met een zinrijke woordspeling zijn naam opnam in zijn kenspreuk: ‘Wacht wel 't slot, castelein’: bewaak goed het u toevertrouwde kasteel; maar ook: let goed op het einde - opnieuw het grote thema waarvan al deze balladen slechts variaties zijn?

Wij weten het niet, we zullen het wel nooit weten. En voorlopig berustende in die onwetendheid, moeten we maar doen als stond er de raad, goed acht te slaan op die acht maal acht. Want zonder het uiterst nauwkeurig in acht nemen van die acht kwadraat gegevens, is er zeker geen kans op resultaat.

4 De vorm ‘in acht houden’ wordt in WNT, deel I, kolom 618 vermeld, zij het met een enkel, niet erg bewijskrachtig citaat uit Cats.

[p. 165]

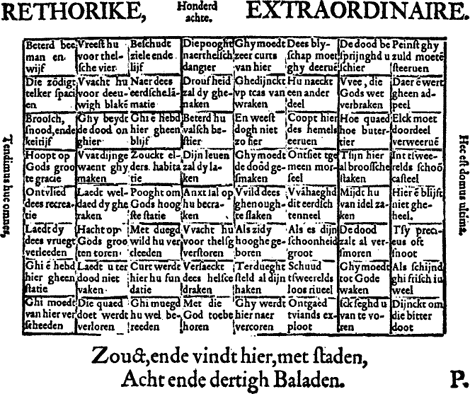II

Men kan het retoricale schaakbord van De Castelein lezen zoals het vóór ons ligt, horizontaal. Dan vindt men acht balladen van acht versregels, alle gekenmerkt door hetzelfde rijmschema

a b a b b c b c

De afwisseling van staand en slepend rijm is daarbij niet steeds eender. De bovenste ballade bezit vier staande en vier slepende rijmen, de derde ook. In de overige zes balladen treft men telkens twee staande tegen zes slepende rijmwoorden aan.

Het is ook mogelijk het schaakbord verticaal te lezen, van boven naar beneden, wat eigenlijk wel zo goed past bij de normale plaatsing van regels poëzie onder elkaar. Dan vindt men opnieuw acht balladen van elk acht verzen en met het eendere rijmschema

a b a b b c b c

Ook hier zijn zes balladen met twee staande en zes slepende rijmen;⁺

+ De oorspronkelijke grootte van het Schaakbord in de editie-1555 is 156 mm breed en 104 mm hoog.

[p. 166]

tegengesteld daaraan zijn de zesde en de achtste kolom, aangezien de balladen daar zes staande en maar twee slepende rijmwoorden bezitten.

Het ligt voor de hand nu ook nog de diagonalen te volgen. De beide balladen die dan ontstaan, gehoorzamen eveneens aan het reeds gevonden rijmschema. De ene heeft een rijmverhouding van vier en vier; de andere evenwel, die links-onder begint, heeft als enige uitzondering niets dan vrouwelijk rijm:

Ghi moedt van hier verscheeden
Laedt u ter dood niet vaken
Met duegd wild hu vercleeden
Anxt sal op hu becraken
Ghy moedt de dood gesmaken
Coopt hier des hemels eeruen
Vvee, die Gods wet verbraken
Peinst ghy zuid moetē steeruen.

Uit deze strofische structuur, voorlopig al achttien maal aangetroffen, mag men de gevolgtrekking maken dat Matthijs de Castelein één bepaalde achtregelige versvorm heeft bedoeld, waarin rijm a twee maal, rijm b vier maal, en rijm c twee maal aanwezig is. Door de plaatsing van rijm b op het einde van de tweede, vierde, vijfde en zevende regel, zijn de twee helften van de ballade ten nauwste met elkaar verbonden en in wezen elkaars spiegelbeeld. In de voortgaande reeks van gekruiste rijmen schept het gepaarde rijm van het vierde en het vijfde vers een opmerkelijk en suggestief effect van innerlijke samenhang. Het is geen toevallige strofe, maar één die De Castelein in zijn Const van Rhetoriken duidelijk bespreekt en met talrijke voorbeeelden toelicht. Op blz. 76 zegt hij in ballade 190⁵:

Een facteur moet weercken ter minster schade
By wijsen rade, daer ic toe wille poghen,
En stellen eerst de snede van daudste balade,
Die eerst was vonden ind sweerelds trade,
Daermen noch boucken af vindt en prologhen:
Dan willick eene ander snede toghen,
Vvaer af tverstand van u werdt vercreghen licht,
Ic hebze uut aude facteurs ghesoghen,
Ende heedt ghecruust oft ouersleghen dicht.

5 Het is de eerste ballade met dit nummer; de tweede met ditzelfde nummer vindt men in de druk van 1555 op blz. 100. Tussen deze twee balladen in ligt een reeks voorbeelden, vandaar de vergissing.

[p. 167]

In de uitvoerige voorbeelden op blz. 77-100 treft men steeds de eendere strofe van acht regels met het eendere rijmschema aan, al is het aantal syllaben van de versregels veel groter. Zo min als bij het schaakbord is hier de verhouding van staande en slepende rijmen blijkbaar een wezenlijk element. Bij de toetsing van de vindbare mogelijkheden naar hun definitieve aanvaardbaarheid zal men daar dan ook niets mee mogen doen.

Voorlopig moeten wij dus volstaan met maar één spelregel: steeds een ‘balade van achten’ en wel ‘ghecruust oft ouersleghen dicht’.

III

De gelijkheid van de gevonden balladen gaat echter veel verder dan het rijmschema alleen: ook de rijmklànk zelf immers is bij herhaling identiek. De eerste horizontale ballade komt met al haar rijmen nauwkeurig terug in de derde ballade: -ijf -ier -ijf -ier -ier -eeruen -ier -eeruen.

Evenzo wordt de tweede ballade herhaald in de vierde en bovendien in de vijfde en de zevende: -acien -aken -atie -aken -aken -eel -aken -eel.

Tenslotte hebben de zesde en de achtste ballade beide de eendere reeks: -eeden -oren -eeden -oren -oren -oot -oren -oot.

Aldus beschouwd heeft men te maken met drie verschillende groepen van onderling gelijkvormige balladen. En aangezien elke ballade met drie rijmklanken uitkomt en zij tezamen het gehele veld bestrijken, staan er in totaal negen rijmen op het spel.

De drie rijmen van de eerste ballade, die daar achtereenvolgens twee maal, vier maal en twee maal worden gebruikt, komen ook voor in de derde ballade; in totaal dus: 4, 8 en 4 maal.

De drie rijmen van de tweede ballade, die daar achtereenvolgens twee maal, vier maal en twee maal worden gebruikt, komen ook voor in de vierde, vijfde en zevende ballade; in totaal dus: 8, 16 en 8 maal.

De drie rijmen van de zesde ballade, die daar achtereenvolgens twee maal, vier maal en twee maal worden gebruikt, komen ook voor in de achtste ballade; in totaal dus: 4, 8 en 4 maal.

Van de negen verschillende rijmen, waar De Castelein mee speelt, vindt men derhalve vier rijmen elk vier maal; vier rijmen elk acht maal; één rijmklank zestien maal.

Om ze gemakkelijker te kunnen onderscheiden, worden de vier viertallen rijmen verder aangeduid als: a, e, i en o;

[p. 168]

de vier achttallen rijmen als: p, q, r en s;

het ene zestienvoudige rijm als: z.

De plaatsing van deze negen rijmklanken op het bord van 64 vakken is uiterst regelmatig.

De rijmen a, e, i en o bevinden zich met hun viertallen elk in één van de vier hoeken: figuur I.

De rijmen p, q, r en s bevinden zich met hun achttallen binnen twee paar horizontale en twee paar verticale stroken, zoals men zich nog wel kan herinneren uit de gelukkige jaren van het matje-vlechten figuur II.

De zestien rijmen z doen hiervoor bepaald niet onder met hun strakke patroon dat horizontaal en verticaal eveneens vier banen omvat en in het midden een onwrikbaar blok van vier gelijke vakken oplevert: figuur III.

Het samenvoegen van deze drie figuren tot de eenheid van het schaakbord, geeft de rijmstructuur daarvan onmiskenbaar duidelijk weer: figuur IV.

Maar deze duidelijkheid bereikt haar maximum, wanneer men de rijmen a, e, i en o aangeeft door grijs, de rijmen p, q, r en s door wit, en het zestienvoudige rijm z door zwart. Er ontstaat dan een geometrische compositie: figuur V, een abstract tegeltableau dat onmiddellijk antwoord geeft op de vraag, hoe veel recht het wel heeft zichzelf een schaakbord te noemen, namelijk géén. Het rijmschema van de ‘balade ghecruust oft ouersleghen’, met juist in het midden een gepaard rijm, heeft een figuur doen ontstaan welke horizontaal, verticaal en langs de twee diagonalen symmetrisch blijkt en zich daarmee wezenlijk onderscheidt van de bekende zwart-wit-structuur, figuur VI, waarvan de symmetrie beperkt is tot de beide diagonalen als as. Toch is het niet waarschijnlijk, dat De Castelein de naam schaakbord énkel heeft gebruikt vanwege het eendere aantal van acht maal acht vakjes. Wie dat meent, onderschat het vernuft van de bourgondische eeuw.

IV

In de schaarse publikaties, totnutoe aan dit schaakbord gewijd, zijn de achtendertig balladen waar De Castelein op doelt, wat al te vlot gevonden. Aan de acht horizontale, acht verticale en twee diagonale gedichten, waarmee wel iedereen begint - en eindigt, heeft zowel de Bibliotheca Belgica (C. 154; Gand-La Haye 1880-1890) als de heer J. van Leeuwen in zijn proefschrift over Matthijs de Castelein (Utrecht 1894) een reeks van twintig andere toegevoegd, die stuk voor stuk verwerpelijk

[p. 169]

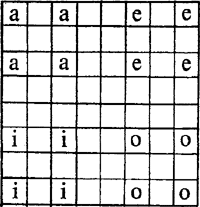
Figuur I
Plaatsing van de vier rijmen die elk vier maal aanwezig zijn.

Figuur II
Plaatsing van de vier rijmen die elk acht maal aanwezig zijn.

Figuur III
Plaatsing van het rijm dat zestien maal voorkomt.

Figuur IV
Overzicht van alle negen rijmen tezamen.

Figuur V
Overzicht van de negen rijmen in grijs, wit en zwart.

Figuur VI
Een gewoon schaakbord, maar met letters en cijfers volgens Dr. J. van Leeuwen.

[p. 170]

zijn. De blokjes in de zeven figuren van de Bibliotheca Belgica, de letteraanduidingen bij Van Leeuwen (blz. 112) geven precies dezelfde achttallen versregels op, maar zonder verwijzing van de ander naar de een, of van hen beiden naar een oudere derde. Toch is er, naar het schijnt, bij deze gelijke opgave ook nog een misverstand.

Zoals de blokjes in de Bibliotheca Belgica⁶ geplaatst zijn, suggereren ze achtereenvolgens: acht hele kolommen; acht hele banen; acht maal twee halve kolommen; acht maal twee halve banen: twee maal twee halve kolommen 4 en 5; twee maal twee halve banen 4 en 5; en tenslotte twee diagonalen. Weliswaar staat nergens in ronde woorden dat men de blokjes zó moet lezen, maar gezien de afwisseling van verticaal en horizontaal, gezien ook de twee gevallen met de vermelding ‘2 ballades’ verticaal langs de linkerzijde van het schaakbord, ligt dit het meest voor de hand. Nu is het aan elkaar plakken van twee halve balladen wel een handeling vol eenvoud, maar toch niet als kenmerk van het ware. Zestien balladen, stuk voor stuk middendoor geknipt en daarna koppen aan koppen, staarten aan staarten weer gehecht, leveren altijd zestien teksten van acht regels op. De vraag rijst evenwel, in hoeverre dit chirurgijnswerk nog op schaken gelijkt. Maar vóór men tijd verspilt op zoek naar geen antwoord, kan men beter eerst nagaan of de teksten wel gehoorzamen aan de spelregel van het rijm. De eerste helft van de eerste verticale ballade, gepaard aan de eerste helft van de tweede verticale ballade, getoetst aan figuur IV, leidt tot het rijmschema:

a r a r p z p z

Dat zijn vier verschillende rijmklanken, waarbij uiteraard ook de noodzakelijke gelijkheid van de vierde en de vijfde versregel ontbreekt. En bij balladen, gemaakt van twee parallelle vershelften uit de vierde en de vijfde kolom, staan we voor de reeks

p z p z p z p z

Dat zijn maar twee verschillende rijmen, en zelfs hier ontbreekt de gelijkheid van de verzen 4 en 5. Daarmee is de Bibliotheca Belgica wel schaakmat. De bijdrage door de heer Van Leeuwen bestaat in een vermakelijke variant op dit verloren spel. Immers ‘de vakken der horizontale rijen van links naar rechts aanwijzend met de cijfers 1-8, die der verticale van beneden naar boven met de letters a-h’, zoals hij op blz. 112 schrijft, dwingt hij ons, allerlei teksten van onder naar boven te lezen. Na de voor-de-hand-liggende acht verticalen en acht horizontalen te hebben genoemd, geeft hij achtereenvolgens:

6 Het zijn telkens uiteraard acht blokjes, hoewel de tekst het heeft over ‘38 ballades de 4 vers chacune’.

[p. 171]

8 balladen overeenkomstig		{ 1. a b c d	{ 1. e f g h	enzovoort;
8 balladen overeenkomstig		{ 2. a b c d	{ 2. e f g h
8 balladen overeenkomstig		{ 1. a b	{ 5. a b
8 balladen overeenkomstig		{ 2. a b	{ 6. a b	enzovoort
8 balladen overeenkomstig		{ 3. a b	{ 7. a b
8 balladen overeenkomstig		{ 4. a b	{ 8. a b
2 balladen	{ 4. a b c d	{ 4. e f g h
2 balladen	{ 5. a b c d	{ 5. e f g h
2 balladen	{ 1. d e	{ 5. d e
2 balladen	{ 2. d e	{ 6. d e
2 balladen	{ 3. d e	{ 7. d e
2 balladen	{ 4. d e	{ 8. d e
(en tenslotte 2 diagonalen.)

Is het al duister, wat er voor schaak schuilt in dit samenrijgen van vier kwartballaden, bij scherp toezien wordt alles nog duisterder. Want met wélke rijmschema's is de lezer nu af-, De Castelein nu op-gescheept! Het eerste voorbeeld, nagespeeld in figuur IV, blijkt:

i r i r q z q z

derhalve vier rijmklanken en geen middenbinding. Het voorbeeld van de tweede groep wordt:

i r q z i r q z

derhalve vier rijmklanken, geen middenbinding, en een zo vreemdsoortig rijmschema dat het zelfs bij De Castelein niet vóórkomt. Het voorbeeld van de derde groep wordt:

g z q z q z q z

en met dit schema is al afgerekend. Het voorbeeld van de vierde groep wordt:

r r z z r r z z

en daar behoeft wel geen woord aan te worden verdaan.

In feite laat dus zowel de Bibliotheca Belgica als de heer Van Leeuwen ons na achttien balladen in de steek. Hun grondfout ligt in de verwaarlozing van het bindende tweetal rijmen midden-in. Uitgaande van die noodzaak, zal men moeilijk een aanvaardbare ballade kunnen vinden die niet in de vierde en de vijfde versregel gebruik maakt van teksten uit de twee aan elkaar grenzende middenkolommen of middenbanen. En hieruit mag men afleiden dat zo'n ballade, van zijkant of bovenkant naar het midden komende, via dit midden zal voortgaan naar de overzijde. Zo lang de onmogelijkheid hiervan niet is gebleken,

[p. 172]

zullen we ook dit als voorschrift aanvaarden. Het retoricale schaakbord is hiermee onderworpen aan twee spelregels:

1.	een vast rijmschema;
2.	een gestadige opschuiving door acht parallelle kolommen of banen.

We zullen eens nagaan, wat dit oplevert.

V

De veelvuldige symmetrie in het schaakbord van De Castelein, dat immers precies gelijk blijft indien men het een kwart, een halve of drie-kwart slag draait, heeft een wiskundig gevolg dat van groot belang is voor het onderzoek naar de daarin opgenomen balladen. Dit namelijk, dat iedere aanvaardbare versvorm die men aantreft, noodwendig minstens vier maal, meestal zelfs acht maal aanwezig moet zijn.

Wat geldig is voor een horizontale reeks in de bovenste helft, is ook geldig voor het spiegelbeeld daarvan in de onderste helft van het bord. Wat geldig is voor een horizontale reeks van links naar rechts, moet ook geldig zijn voor een verticale reeks van boven naar beneden, voor een horizontale reeks van rechts naar links, en voor een verticale reeks van beneden naar boven.

Verdubbeld dus door z'n spiegelbeeld, en bovendien verviervoudigd door de draaiing met respectievelijk 90, 180 en 270 graden, levert één gevonden resultaat onmiddellijk acht resultaten op. Er is echter een uitzondering, en wel daar waar de ballade gelezen wordt langs de diagonalen. Doordat hier telkens twee van de mogelijkheden samenvallen, zijn er niet acht, maar in totaal slechts vier. Voegt men alle mogelijkheden uit alle mogelijke richtingen bijeen, dan moet de hoeveelheid balladen, in dit schaakbord ondergebracht, dus voldoen aan de formule: 8 × + 4.

Onder zijn opgave heeft De Castelein zelf meegedeeld, hoeveel volwaardige gedichten hij aanwezig achtte:

Zouct, ende vindt hier, met staden,
Acht ende dertigh Baladen.

Maar juist wanneer men ‘met staden’, derhalve bedaard, systematisch en met kalm overleg te werk gaat, zal men 38 moeten houden voor een vrij zonderling getal. Het is niet deelbaar door 4, het kan dus geen uitkomst zijn van de viervoudige symmetrie. Men moet daarom veronderstellen, dat de auteur hetzij de retrograden, hetzij de verticalen, hetzij allebeide heeft uitgesloten.

Nu staat er verticaal langs de rechter- en de linkerkant van zijn

[p. 173]

schaakbord een latijnse spreuk, die in dit verband het overwegen wel waard is: Hec est domus ultima; en: Tendimus huc omnes. Bij een dichtwerk dat voortdurend over sterflijkheid, dood en graf handelt, wekken die spreuken geen verbazing: Wij zijn allen op weg hierheen; en: Dit is de laatste woning. Toch is het niet ondenkbaar, dat de eerste persoon meervoud, die in ‘tendimus’ is opgenomen, niet enkel de mensen betreft maar ook de balladen. En in zo'n geval zou ‘domus’, behalve het graf als laatste behuizing, ook het vakje van de laatste versregel betekenen. Aldus aanduidende dat links én rechts het eindpunt ligt, zou de dichter zowel de normale leesrichting als de retrograde hebben bedoeld. Het aantal balladen waar het om gaat, is dan eigenlijk niet langer 38, maar twee maal 19.

In de gelijkvormige structuur van boven- en benedenhelft van dit schaakbord is echter geen mogelijkheid denkbaar, die zich niet zou weerspiegelen. Iedere aanvaardbare reeks boven het midden, moet ook aanwezig zijn beneden het midden. Een oneven aantal, zoals 19, kán daarom niet juist zijn. Op grond hiervan zullen we moeten concluderen, dat De Castelein zijn aantal van 38 niet kan hebben bedoeld voor de twee horizontale richtingen vice versa gezamenlijk, noch voor de twee verticale richtingen vice versa gezamenlijk.

Er is dus een derde spelregel: de retrograden tellen niet mee.

Er zijn nu nog maar twee mogelijkheden open: of één horizontale plus één verticale richting; of slechts één enkele richting, bijvoorbeeld van links naar rechts, horizontaal. Indien de spreuk langs de linkerzijde bedoeld was geweest om ons tot deze opvatting te verplichten, had er niet ‘huc’ moeten staan, maar ‘hinc’. Als leesfout in middeleeuws schrift, als drukfout in een zestiende-eeuws boek dat niet eens door de auteur zelf ter perse is gelegd, lijkt het geenszins onmogelijk. En al verliezen die latijnse woorden, gewijzigd, ook hun toepasselijkheid op de dood, ze worden allerminst zinledig: juist in de linkerkolom immers vindt men allerlei versregels als: Ontvlied dees recreatie; en: Ghi moedt van hier verscheeden.

Maar dit zijn louter veronderstellingen. Indien we voorlopig de linkerkolom als uitgangspunt kiezen bij het verdere onderzoek, is dat slechts een werkhypothese, een hulpmiddel terwille van de gewenste overzichtelijkheid, geen voorschrift, geen wet, en dus allerminst gelijkwaardig aan de drie nu geldende spelregels:

1.	een vast rijmschema;
2.	een regelmatige volgorde van de gebruikte kolommen of banen;
3.	geen retrograden.

[p. 174]

VI

Beperkt men zich tot deze drie spelregels alleen, dan blijkt al gauw dat er vele honderden, zelfs vele duizenden mogelijkheden bestaan. Na elk der acht versregels uit de eerste kolom zou immers elk der acht versregels uit de tweede kolom kunnen worden gekozen. Dat maakt reeds 64 verschillende variaties. En deze zijn reëel, want bij dit eerste paar opeenvolgende verzen is er nog geen beperkend rijmschema, terwijl ook hun betekenis of zinsbouw geen moeilijkheden oplevert. Dat komt doordat De Castelein al de vakjes van zijn schaakbord heeft gevuld met zelfstandige, zoveel mogelijk in zichzelf besloten syntactische eenheden, die bovendien ongeveer gelijk zijn van inhoud. Kiest men naar willekeur een handvol versregels uit, dan krijgt men weinig anders te lezen dan dat het leven kort duurt, snel voorbijgaat, hachelijk en jammerlijk is; dat de dood ieder bedreigt, niemand ontziet of spaart, niet kan worden uitgesteld; dat men het aardse moet verzaken, de deugd betrachten, de hel vrezen en zich richten naar God. Het zijn geen opzienbarende denkbeelden, nieuw van visie of bewogen van persoonlijke zielenood. Integendeel: het is de algemene en gemiddelde vergankelijkheidsmoraal van de christelijke middeleeuwen in heel West-Europa, het is de zin van alle dodendansen, van ettelijke refreinen in 't vroede, van dozijnen liederen, de zin ook van de Elckerlyc.

De Castelein heeft deze strekking ernstig en waardig onder woorden gebracht, zo beknopt mogelijk, met maar zes of zeven lettergrepen per keer, in 28 gevallen als een gebiedende wijs, in 25 gevallen als een hoofdzin met daarin dikwijls nog de formule: ghy moet. Aldus zijn 53 van de 64 vakjes gevuld; de overige elf bevatten zinsconstructies die zich zonder onoverkomelijke bezwaren kunnen voegen bij een voorafgaande of volgende imperatief of hoofdzin, en maar nauwelijks variatie brengen in de heersende monotonie van het doodsvermaan: een vorm overigens, niet ongepast voor de monotone heerschappij van het dood-gaan en de dood.

Kan men na elk van de eerste acht versregels dus op acht manieren een tweede versregel kiezen, ten aanzien van de derde is men vanwege het rijm niet meer zo vrij. Wie met rijm a of i begonnen is, moet nu doorgaan met a of i, en heeft in de derde kolom dus maar twee mogelijkheden. Wie met rijm r begonnen is, kan in de derde kolom nog kiezen uit vier. Dit systeem van hetzij twee, hetzij vier mogelijkheden bij de overgang van elke vorige naar elke volgende kolom, betekent dat iedere versregel uit kolom 1, die door toevoeging van zeven achtereenvolgende regels uitgroeit tot een aanvaardbare ballade, de beschik-

[p. 175]

king heeft over een aantal mogelijkheden waarvan het minimum ligt in de formule 2⁷, het maximum in de formule 4⁷.

Om concreet te zijn: bij het rijmschema a p a p p e p e, dat op twee plaatsen kan beginnen en op 2⁷ manieren kan worden voortgezet, zijn er dus 2⁸ = 256 verschillende mogelijkheden.

Bij het rijmschema r z r z z s z s, dat op vier plaatsen kan beginnen en op 4⁷ manieren kan worden voortgezet, zijn er 4⁸ = 65.536 verschillende mogelijkheden, die allemaal aan de drie spelregels voldoen.

En dit is nog niet alles. Er zijn nog méér rijmschema's, en daarvoor gelden wiskundige formules waarin niet alle acht factoren óf een 2 óf een 4 zijn. Tussen het minimum-schema met maar 256 variaties en het maximum-schema met 65.536 variaties in, zijn er nog rijmschema's te vinden met 2⁶ × 4² = 1.024; met 2⁴ × 4⁴ = 4.096; en met 2² × 4⁶ = 16.384 mogelijkheden. Aldus gaat het totale aantal de honderdduizend ver te boven.

Zo lang men zich houdt aan niet anders dan de drie spelregels, bevindt men zich nog in een rijk van haast onafzienbare mogelijkheden. Dat is een werkelijkheid die zich niet laat weerleggen. Immers, ook de volgende tekst is in alle betekenissen een redelijke ballade, al springt men wat wild van vakje naar vakje in kolom na kolom:

Beterd bee man en wijf	kolom 1 vak 1
Laedt weldaed dy gheraken	kolom 2 vak 5
Ghi ēd hebd hier gheen blijf	kolom 3 vak 3
Versaeckt dees helsce draken	kolom 4 vak 7
Ghy moedt de dood gesmaken	kolom 5 vak 4
Hu naeckt een ander deel	kolom 6 vak 2
Mijdt hu van idel zaken	kolom 7 vak 5
Daer ē wert gheen adpeel.	kolom 8 vak 2

Men moet aannemen dat Matthijs de Castelein zich hiertegen zou hebben verzet, niet echter omdat de inhoud onzin of de vorm geen goede ballade van achten zou zijn. Indien het getal 38 dat hij noemt, zoveel minder is dan de vele tienduizenden vindbare en op zichzelf ook bruikbare variaties, ligt de oorzaak dáárin, dat hij allerlei onordelijke sprongen heeft willen vermijden als tegenstrijdig aan de strenge voorschriften van het schaakbord.

Er zal dus tenminste een vierde spelregel moeten zijn, die onze vrijheid verder beperkt.

[p. 176]

VII

Men kan veronderstellen dat De Castelein bedoeld heeft schaak te spelen met een pion. Dit houdt dan in, dat men, kolom na kolom van links naar rechts opschuivende, telkens ten hoogste drie mogelijkheden heeft: schuin naar boven, horizontaal, of schuin naar beneden. In zeven kolommen zou dat nog kunnen leiden tot het respectabele aantal van 3⁷, ware het niet dat het dwingende rijmschema telkens één of zelfs twee mogelijkheden uitsluit. Deze beperking geldt echter meer voor de bovenste en onderste banen van, het bord, waar zich de bescheiden rijmen a, e, i en o bevinden, dan voor de middenbanen met de enorme mogelijkheden van het zestienvoudige rijm z. Een simpele proef op de som brengt het bewijs.

Wij zetten onze pion binnen de eerste kolom op het vierde vakje van boven. ‘Hoopt op Gods groote gracie’ staat er bemoedigend. Het is een rijm r dat in totaal acht maal vóórkomt.

Vanuit dit vakje kunnen we op drie manieren verder, namelijk naar kolom 2 vak 3 (rijm p); naar kolom 2 vak 4 (rijm z); en naar kolom 2 vak 5 (rijm z).

De derde versregel, te ontlenen aan kolom 3, moet eindigen op de rijmklank van de eerste regel, dus r. Vanuit kolom 2 vak 3 zijn er twee van zulke vakjes bereikbaar, namelijk kolom 3 vak 2; en kolom 3 vak 4.

Vanuit kolom 2 vak 4 zijn er ook twee van zulke vakjes bereikbaar, namelijk kolom 3 vak 4; en kolom 3 vak 5.

Vanuit kolom 2 vak 5 zijn er eveneens twee van zulke vakjes bereikbaar, namelijk ook kolom 3 vak 4; en kolom 3 vak 5.

Nu is de ballade nog maar drie versregels ver, en reeds zijn er zes mogelijkheden:

een met kolom 3 vak 2 als derde versregel;

een met kolom 3 vak 4 als derde versregel, en in de tweede regel rijm p;

twee met kolom 3 vak 4 als derde versregel, en in de tweede regel rijm z;

twee met kolom 3 vak 5 als derde versregel, en in de tweede regel rijm z.

Het toevoegen van de vierde versregel vermeerdert uiteraard het aantal mogelijkheden nog, al houdt de plicht om te rijmen op de tweede versregel deze uitbreiding in bedwang. Aldus:

na kolom 3 vak 2 kan de vierde versregel worden ontleend aan kolom 4 vak 1, of aan kolom 4 vak 3; hier zijn derhalve twee mogelijkheden;

[p. 177]

na kolom 3 vak 4 bestaat er voor het volgende rijm p maar een mogelijkheid, namelijk kolom 4 vak 3;

na kolom 3 vak 4 zijn er voor het volgende rijm z twee mogelijkheden, namelijk kolom 4 vak 4; of kolom 4 vak 5;

na kolom 3 vak 5 zijn er voor het volgende rijm z dezelfde twee mogelijkheden: kolom 4 vak 4; of kolom 4 vak 5.

Gecombineerd met de reeds vastgestelde variaties tot en met de derde versregel, ontstaat nu voor de halve ballade het volgende aantal:

1 × 2 plus 1 × 1 plus 2 × 2 plus 2 × 2, tezamen 11 mogelijkheden. Daarvan is kolom 4 vak 1 bereikt langs maar één weg;

kolom 4 vak 3 bereikt langs twee wegen;

kolom 4 vak 4 bereikt langs vier wegen;

kolom 4 vak 5 bereikt langs vier wegen.

Nu zal echter de vijfde versregel moeten rijmen op de vierde. Bij kolom 4 vak 1 bestaat daartoe slechts de horizontale opschuiving naar kolom 5 vak 1; het aantal van 1 blijft dus gelijk.

Bij kolom 4 vak 3 bestaat er evenmin enige keuze dan kolom 5 vak 3; het aantal van 2 blijft dus ook gelijk.

Kolom 4 vak 4 heeft in het hart van het schaakbord echter twee mogelijkheden, zodat het aantal van 4 nu wordt verdubbeld tot 8.

Ditzelfde geldt van kolom 4 vak 5; ook daar wordt 4 tot 8.

De ballade, gevorderd tot en met de vijfde versregel, heeft dus reeds 1 + 2 + 8 + 8 = 19 variaties.

Wie nu voorzichtig verderschuift, kan metterdaad constateren dat er voor het voltooien van de ballade vanuit kolom 5 vak 1 nog vier verschillende mogelijkheden bestaan:

dat er voor de voltooing vanuit kolom 5 vak 3 nog zes verschillende mogelijkheden bestaan; rekening houdende met de twee verschillende wegen daarvóór, bezitten wij dus twaalf varianten;

dat er voor de voltooiing vanuit kolom 5 vak 4 nog elf mogelijkheden bestaan, namelijk 3 met eindrijm e en 8 met eindrijm s; gecombineerd met de acht verschillende wegen erheen, leidt dit tot 88 variaties;

dat er voor de voltooiing vanuit kolom 5 vak 5 eveneens elf mogelijkheden bestaan, dus in totaal ook 88 variaties.

Spelende met één pion, nooit anders schuivende dan een pion mag doen, stipt gehoorzamende aan het rijmschema, kan ieder die begint bij ‘Hoopt op Gods groote gracie’ dus rekenen op de zegenrijke oogst van 4 + 12 + 88 + 88 volwaardige balladen, oftewel 192 in totaal.

De aanvangsregel in kolom 1 vak 5 levert als spiegelbeeld ook 192 mogelijkheden op. Dat is tezamen 384. En al zijn de aantallen boven

[p. 178]

en onder deze vruchtbare middenstrook wat kleiner, een paar honderd bruikbare balladen liggen er vlot voor een pion te grijp.

Ook zó heeft De Castelein zijn spel kennelijk niet bedoeld. En terecht niet: de pion immers heeft zijn standplaats in de tweede kolom; de eerste is hem principieel ontzegd.

De vierde spelregel luidt dan ook: alleen gekwalificeerde schaakstukken worden gebruikt.

VIII

Het ligt voor de hand, nu uit te gaan van de veronderstelling, dat de stukken in de linkerkolom zo zijn opgesteld als bij een echt schaakspel, van boven naar beneden dus: kasteel, paard, raadsheer, koning, koningin, raadsheer, paard en kasteel.

Het kasteel, geplaatst in kolom 1 vak 1, heeft onder de beperkende omstandigheid dat iedere volgende versregel moet worden ontleend aan iedere volgende kolom, veel van zijn kracht verloren. Het kan niets anders meer doen dan zich horizontaal bewegen van links naar rechts, met als resultaat slechts één ballade.

Het paard, geplaatst in kolom 1 vak 2, kan geen sprong maken naar boven, dan raakt hij buiten het bord, en ook niet naar voren, dan komt hij terecht in de derde kolom. Zijn enige mogelijkheid is dus naar beneden, naar kolom 2 vak 4, en dit gaat uitstekend. Vandaar weer omhoog naar kolom 3 vak 2, omlaag naar kolom 4 vak 4, omhoog naar kolom 5 vak 2, enzovoort. Het resultaat van dit springconcours is een voortreffelijke tekst, maar ook slechts één:

Die zōdigt telker spacien
Vvat dijnge waent ghy maken
Naer dees eerdsche lāmatie
n leuen zal dy laken
Ghedijnckt vp tcas van wraken
Ontsiet tgemeen morseel
Vvee, die Gods wet verbraken
Int tsweerelds schoō casteel.

De raadsheer, geplaatst in kolom 1 vak 3, kan in schuine richting twee kanten uit, namelijk naar kolom 2 vak 2, of naar kolom 2 vak 4. De voortzetting is in het eerste geval op twee manieren mogelijk, namelijk naar kolom 3 vak 1, of naar kolom 3 vak 3; in het andere geval slechts op één manier, kolom 3 vak 3, aangezien kolom 3 vak 5 geen goed rijm oplevert. Ook de mogelijkheden in kolom 4 en de aanslui-

[p. 179]

ting daarvan naar kolom 5 zijn beperkt, immers de versregels ontleend aan de kolommen 4 en 5 moeten op elkaar rijmen. In de schuine richtingen, de enige die de raadsheer zijn toegestaan, is de mogelijkheid voor dit gepaarde rijm slechts aanwezig in het hart van het bord: het opmerkelijke blok van de vier rijmen z. De ballade, begonnen in kolom 1 vak 3, moet dus kolom 4 vak 4 bereiken om via kolom 5 vak 5 zich verder te kunnen ontwikkelen. Tot aan dit overgangspunt toe zijn er vanuit kolom 1 vak 3 maar twee wegen: hetzij via kolom 2 vak 2, hetzij via kolom 2 vak 4.

Aan de zijde, rechts van dit overgangspunt zijn de mogelijkheden echter wat groter, en wel vier. De ballade kan namelijk op één manier uitkomen bij kolom 8 vak 4; op twee verschillende manieren bij kolom 8 vak 6; en op één manier bij kolom 8 vak 8. De raadsheer, die langs twee onderscheiden wegen kolom 4 vak 4 heeft kunnen bereiken en van kolom 5 vak 5 langs vier wegen verder kan gaan, brengt dus in totaal acht verschillende balladen tot stand.

Het zijn maar kleine aantallen: 1 voor het kasteel, 1 voor het paard, 8 voor de raadsheer, tezamen 10. Maar ze moeten worden verdubbeld wegens de mogelijkheden op de onderste helft van het bord. Dat maakt 20 in totaal.

Nu zou het wel mooi zijn, indien koning en koningin, gezeteld in kolom 1 vak 4 en vak 5, zich bij hun tochten over het veld wilden bepalen tot nog precies 18 variaties. Maar hoewel de koningin heel veel, de koning maar heel weinig mag doen zo lang het om echte schaakstukken gaat, hebben de drie dwingende spelregels hen beiden vernederd tot de positie van een pion, al kunnen ze dan stelling nemen in de eerste kolom. Ook zij doen maar drie schreden: schuin naar boven, recht vooruit, of schuin naar beneden. En daar ze geplaatst zijn in de middenstrook met z'n veelvuldigheid van gelijke rijmen, geldt voor elk van hen het aantal mogelijkheden dat bekend is door de proef op de som van de pion. Het zijn er 192.

Aldus is deze aantrekkelijke opstelling van de schaakstukken uitgelopen op de reeks van 1 + 1 + 8 + 192 + 192 + 8 + 1 + 1 gevarieerde balladen; dat is 404 in totaal. En opnieuw moeten we constateren, dat dit in verhouding tot de achtendertig waar De Castelein van spreekt, wat véél is. Het is dan ook niet waarschijnlijk, dat koning en koningin binnen de gekozen begrenzing blijven. En evenmin is het waarschijnlijk, dat de schrijver juist vier van de meest voor de hand liggende balladen, namelijk die van de horizontale banen 2, 3, 6 en 7, zou hebben uitgesloten, zoals nu eenmaal gebeurt wanneer men de

[p. 180]

linkse vakjes daarvan enkel gebruikt als startplaats van paard en raadsheer, het zij met alle eerbied gezegd.

Op grond van het bovenstaande moet de vierde spelregel nu nader worden gepreciseerd en wel als volgt:

alleen kasteel, paard en raadsheer worden gebruikt, maar zonder te zijn gebonden aan hun eigenlijke uitgangspunt.

IX

Omdat de grote getallen ons blijven hinderen, zullen we niet moeten zoeken naar de mogelijkheden alleen, maar ook naar de meest voor de hand liggende waarschijnlijkheden daaruit. Voordat we dit kunnen beoordelen, dienen we een volledige inventaris te maken van wat er nu werkelijk kàn, na de nieuwe beperking tot kasteel, paard en raadsheer.

Met het kasteel als speelstuk is er uit elk van de acht vakjes links telkens maar één mogelijkheid. Het totale aantal is dus: 8.

Met het paard als speelstuk blijkt men vanuit elk vakje links een voortreffelijke reeks te kunnen maken, geheel volgens het rijmschema. Het paard maakt daarbij steeds gebruik van twee parallelle banen. Beginnende in kolom 1 vak 1, springt het over naar kolom 2 vak 3, dan naar kolom 3 vak 1, verder naar kolom 4 vak 3, enzovoort. Beginnende in kolom 1 vak 2 springt het paard evenzo eerst naar beneden, dan weer naar boven, enzovoort. Beginnende in kolom 1 vak 3 of vak 4 springt het paard echter eerst naar boven, daarna naar beneden. Aldus ontstaan er in totaal acht mogelijkheden, uit elk vak één.

Toch zijn hiermee de variaties van het paard niet uitgeput. Bij nauwkeurig toezien is namelijk ook een reeks mogelijk, met voortreffelijk rijmschema, die vanuit kolom 1 vak 3 naar kolom 2 vak 5 springt, voorts naar kolom 3 vak 3, naar kolom 4 vak 5, en verder dalende naar kolom 5 vak 7, dan naar kolom 6 vak 5, naar kolom 7 vak 7, en tenslotte naar kolom 8 vak 5. De ballade luidt dan als volgt:

Broosch, snood, ende keitijf
Laedt weldaed dy gheraken
Ghi ē hebd hier gheen blijf
Anxt sal op hu becraken
Ter dueght steld al dijn haken
Vvāhaeghd dit eerdsch tenneel
Ghy moedt tot Gode waken
Hier ē blijft niet gheheel.

[p. 181]

Er is vanuit kolom 1 vak 3 zelfs nog een derde mogelijkheid voor het paard, namelijk eerst kolom 2 vak 1, kolom 3 vak 3 en kolom 4 vak 1; daarna via kolom 5 vak 3, kolom 6 vak 5 en kolom 7 vak 3 naar kolom 8 vak 5.

Deze zelfde varianten zijn mogelijk vanuit kolom 1 vak 4, en overeenkomstig de spiegelbeelden ook uit kolom 1 vak 5 en vak 6. In totaal heeft het paard dus 4 × 1 plus 4 × 3, dat is zestien mogelijkheden, maar acht daarvan zijn voor het oog bepaald regelmatiger dan de rest.

De raadsheer heeft nooit kans het noodzakelijke dubbelrijm van regel 4 en 5 in zijn schuine spelrichtingen te verwezenlijken, tenzij enkel in het hart van het bord. Daaruit volgt, dat hij niet kan beginnen vanuit kolom 1 vak 2 en vak 7. De mogelijkheden daar zijn nihil. Vanuit kolom 1 vak 1 heeft hij maar één weg om kolom 5 vak 5 te bereiken; van dat punt uit bestaan er, zoals we reeds hebben gezien, vier mogelijkheden om de ballade in schuine richtingen te voltooien.

Begint de raadsheer in kolom 1 vak 3, dan kan hij op twee manieren kolom 5 vak 5 bereiken, en vandaar op vier manieren verder gaan; in totaal dus acht.

Begint de raadsheer in kolom 1 vak 5, dan kan hij langs een zig-zagweg kolom 5 vak 5 bereiken, vanwaar hem opnieuw vier mogelijkheden ter beschikking staan.

De spiegelbeelden van deze uitgangspunten, namelijk de vakken 8, 6 en 4, verschaffen respectievelijk eveneens vier, acht en vier variaties.

Langs de gehele linkerzijde beschikt de raadsheer dus over 32 mogelijkheden. Het is echter duidelijk dat de meeste daarvan een weliswaar wetmatige, maar voor het oog tamelijk grillige gang over het bord betekenen, zodat ze ondanks alle verdere kwaliteiten, waaronder een voortreffelijk rijmschema, toch onwaarschijnlijk moeten heten. Uiterst waarschijnlijk daarentegen zijn bij de raadsheer alleen vier volstrekt regelmatige lijnen: namelijk de twee diagonalen, en de twee doorgaande zig-zag-wegen in de dubbele middenbaan. Bijvoorbeeld:

Hoopt op Gods groote gracie
Laedt weldaed dy gheraken
Zouckt elders habitatie
Anxt sal op hu becraken
Ghy moedt de dood gesmaken
Vvāhaeghd dit eerdsch tenneel
Tsijn hier al broossche staken
Hier ē blijft niet gheheel.

[p. 182]

Resumerende hebben we dus nu gevonden:

8 mogelijkheden van het kasteel, steeds regelmatig;

16 mogelijkheden van het paard, waarvan 8 geheel regelmatig;

32 mogelijkheden van de raadsheer, waarvan maar 4 geheel regelmatig.

Van één zijde uit beginnende, steeds het rijmschema aanhoudende, steeds in eendere richting opschuivende, spelende met maar drie gekwalificeerde schaakstukken, beschikken we over 56 mogelijkheden. Maar slechts 20 daarvan bewegen langs lijnen van feilloze regelmaat.

Iedere poging om deze 20 uit te breiden tot 38, hetzij door toevoeging van 18 van de raadsheer, tenzij door toevoeging van 8 van het paard en 10 van de raadsheer, mislukt, omdat de afgewezen mogelijkheden niet slechter zijn dan de rest. Dit feit verplicht ons, de absolute regelmaat van de looplijnen als vijfde voorschrift te aanvaarden. We zullen dan echter meteen afstand moeten doen van de veronderstelling dat slechts één richting, horizontaal óf verticaal, in aanmerking komt. Die werkhypothese heeft haar dienst nu wel gedaan.

X

Nu men ervan mag uitgaan dat De Castelein zowel de horizontale als de verticale richting heeft bedoeld, moet elk gevonden aantal worden verdubbeld, althans bijna elk.

Het kasteel, met acht mogelijkheden per richting, komt nu op	16
Het paard, met acht regelmatige mogelijkheden per richting, komt nu op	16
De raadsheer, met twee regelmatige zigzaglijnen in de middenbanen, komt nu dank zij de middenkolommen op	4
De raadsheer, met twee regelmatige mogelijkheden langs de diagonalen, blijft wegens de uitgesloten retrograden echter bij	2
	_____
Totaal voor de drie speelstukken gezamenlijk	38

Voor alle duidelijkheid kan men dit verrassende resultaat ook nog op een andere wijze formuleren:

horizontaal:	8 maal met het kasteel
	8 maal met het paard
	2 maal met de raadsheer
verticaal:	8 maal met het kasteel
	8 maal met het paard
	2 maal met de raadsheer
diagonaal:	2 maal met de raadsheer
	_____
Totaal	38 maal met alle drie schaakstukken; zie figuur VII.

[p. 183]

Figuur VII
De looplijnen van de schaakstukken bij De Castelein:
1. Kasteel, acht keer, en acht keer verticaal;
2. de raadsheer, twee keer, en twee keer verticaal;
3. het paard, acht keer, en acht keer verticaal;
4. de raadsheer, diagonaal, twee keer.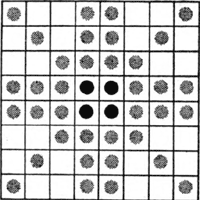

Figuur VIII
Frequentie van de gebruikte versregels:
geheel wit: vier maal, namelijk twee maal door het kasteel en twee maal door het paard; grijs: vijf maal, namelijk bovendien door de raadsheer; zwart: zeven maal, waarvan drie maal door de raadsheer.

Tijdens deze dichterlijke bewerkingen wordt het bord bij herhaling in z'n geheel gebruikt. Het kasteel, horizontaal en verticaal, laat alle 64 versregels elk tweemaal aan bod komen. Het paard, horizontaal en verticaal, laat opnieuw alle 64 versregels elk tweemaal aan bod komen. Dat is vier maal. De raadsheer, horizontaal, maakt dat 16 versregels elk nogmaals, dus voor de vijfde keer, nodig zijn. De raadsheer, verticaal, maakt dat opnieuw 12 versregels voor de vijfde maal, en 4 nu voor de zesde maal nodig zijn. De raadsheer, diagonaal, voegt er nog 12 als vijf maal gebruikt aan toe, en maakt dat het centrale viertal nu voor de zevende maal gebezigd wordt. De slotsom is, dat van de 64 versregels er 24 elk vier maal, 36 elk vijf maal, en 4 elk zeven maal in actie zijn: figuur VIII. Men bedenke wel, wat dit inhoudt: het zevenvoudig gebruik van zo'n versregel betekent zeven relaties achterwaarts, zeven relaties voorwaarts, en wegens het rijm ook nog zeven relaties op één versregel afstand. Het is dus wel duidelijk wáárom De Castelein de raad gaf ‘ant cruce eerst’ te beginnen: daar, en speciaal in het hart daarvan, zit inderdaad de crux. Achttien van de achtendertig balladen maken van een of twee der vier centrale vakjes in wisselende combinaties gebruik, en zeker behoren zij mede tot de allermooiste resultaten:

[p. 184]

 

Ghy moedt zeer curts van hier

 

Droufheid zal dy ghenaken

 

En weest dogh niet zo fier

 

Dijn leuen zal dy laken

 

Vvild dees ghenoughte slaken

 

Vvacht hu voor thelsg verstoren

 

Ter dueght steld al dijn haken

 

Met die God toebehoren.

Het lijkt mij moeilijk er nog aan te twijfelen, of Matthijs de Castelein inderdaad deze 38 balladen zal hebben bedoeld. Zij immers, en zij alleen, voldoen aan niet minder dan vijf spelregels tegelijk:

1.	het vaste rijmschema van de ballade van achten, ghecruust oft ouersleghen;
2.	het achtereenvolgens ontlenen van de acht versregels aan acht kolommen naast elkaar of aan acht banen onder elkaar;
3.	geen retrograden;
4.	een volgorde van de versregels overeenkomstig de schaakwijze van kasteel, paard en raadsheer;
5.	uitsluitend speellijnen van volstrekte regelmaat.

Buiten deze achtendertig balladen is er geen enkele vindbaar, die aan de eendere voorwaarden voldoet. Het meesterschap van De Castelein bestaat hierin, dat hij zijn vijf spelregels met uiterste consequentie heeft toegepast, al heeft hij ze niet openlijk geformuleerd. Ze liggen in het spel zelf, en dat heeft ze tenslotte nu wel prijsgegeven. Het zijn deels àndere regels dan bij het schaken, zoals ook het bord ànders is dan een schaakbord. Het zij zo. Misschien is dan toch de poëzie, zelfs bij de rederijkers, nog iets ànders dan een vernuftig spel.

g. stuiveling