Graph G 1 legt de ‘links van’-relaties vast, die gelden voor deze groepen. In deze graph staat PC voor een element als in in het bos in of inslapen, St voor een woord dat de stam van het hoofdwerkwoord bevat, Pv voor de persoonsvorm, Infh voor de infinitief van een z.g. hulpwerkwoord van tijd of lijdende vorm; X en Y zijn variabelen.
| G 1 |

|
In de niet-perifrastische o.t.t. en o.v.t. maakt de stam van het hoofdwerkwoord deel uit van de persoonsvorm, die tevens de enige werkwoordsvorm is. Anders gezegd: voor o.t.t. en o.v.t. geldt Pv = St, Infh = Φ. Uit G 1 kan dus de volgende graph worden afgeleid:
Een voorbeeld is insliep; de volgorde sliep in is slechts denkbaar als het resultaat van ‘Verb second’-plaatsing.
Het enige verontrustende tot dusver zijn de vraagtekens in (2). Hieruit kan worden afgeleid dat de combinatie van Pv en Infh ondoordringbaar is voor PC en St. Anders gezegd: Pv en Infh gedragen zich ten opzichte van PC en St als één element:
| (2) |
g |
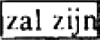 ingeslapen ingeslapen |
| |
j |
in 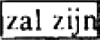 geslapen geslapen |
| |
i |
ingesl, 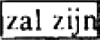 |
De regel Pv → Infh beschrijft de ‘interne’ volgorde van de onderdelen van dit element, in de volgende eveneens van G 1 afgeleide graph door H aangeduid:
| G 3 |
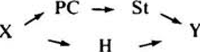
|
Het op deze wijze ingevoerde niveauverschil tussen de elementen Pv en Infh eneren X, PC, St en Y anderzijds is geen op zichzelf staand verschijnsel. De welbekende en goed te funderen PP over V-transformatie is op een dergelijk niveauonderscheid gebaseerd.
De volgorde Pv Infh lijkt niet samen te hangen met de eigenschappen van persoonsvorm en infinitief, getuige (2c). Eerder kan men denken aan een obligate volgorde van de Pv en één of meer hulpwerkwoordsinfinitieven, als uitdrukking van een bepalingshiërarchie (Van Bakel 1969: 203 vgg) zoals in de volgende zin:
| (3) |
ik dan wel eens zou hebben willen blijven staan kijken |
Uit deze zin valt af te leiden dat evenals H, ook Infh moet worden beschouwd als de aanduiding van een reeks elementen, die zich ten opzichte van andere elementen als één element gedraagt: Infh1 (Infh2, ..., Infhn). Als St een infinitief is, dan is de volgorde van H en St niet meer vrij. In G 4 is deze stand van zaken uitgedrukt: