Roeping. Jaargang 1

[p. 44]

Over rythmiek en voordracht in de toonkunst.

Er is geen kunst, die met meer abstracte middelen voortgebracht wordt dan de toonkunst. Immers de schilder- en beeldhouwkunst hebben als materiaal doek, verf en klei, de woordkunst het gesproken woord, waarmee men onmiddellijk duidelijk kan uitdrukken, wat men gevoelt. De toonkunst beschikt echter over de twee zeer abstracte materialen: lucht en tijd. Immers men onderscheidt: hoogte of laagte, sterkte of zwakte van tonen, hun klankkleur (scherp of week).

Verder langeren of korteren duur en daardoor zwaarder of lichter karakter van tonen.

Een toon ontstaat door het regelmatig trillen der lucht, veroorzaakt door de regelmatige trillingen van een veerkrachtig lichaam, muziekinstrument geheeten.

Een muziekinstrument maakt dus den toon niet, maar is enkel een gereedschap, om de lucht aan het trillen te brengen. Of dat instrument nu is het menschelijk spreekorgaan of een mechanisch apparaat, doet aan de hoogte of laagte van een toon niets af en heeft uitsluitend invloed op de klankkleur. Hoe grooter het aantal trillingen binnen een bepaald tijdsverloop is, hoe hooger de toon zal zijn, hoe minder het aantal trillingen, hoe lager de toon.

Hier ziet men dus de eerste verhouding, of beter gezegd de eerste tegenstelling in de toonkunst. Die tegenstelling kan natuurlijk scherper of zwakker gemaakt worden, in verband met de meerdere of mindere overeenkomst van twee tonen. Hoe eenvoudiger de verhouding der trillingsgetallen van twee tonen, hoe minder ook hun tegenstelling, hoe ingewikkelder die verhouding, des te meer hun tegenstelling. Op deze verhouding der trillingsgetallen is de geheele harmonie- of accoordenleer gebaseerd.

De hoedanigheid van de klankkleur wordt eveneens veroorzaakt door de luchttrillingen, niet door het aantal binnen een bepaald tijdsverloop, maar meer door het karakter dier trillingen, wat natuurlijk een zeer groote verscheidenheid kan geven. Hierop is vooral van invloed de vorm of de bouw van het instrument, waarmee de lucht aan 't trillen gebracht wordt. Zoo geeft b.v. een violoncel een geheel andere kleur aan den toon dan een viool, wat zeer duidelijk te bemerken is, als zij denzelfden toon doen voortbrengen en dus het aantal trillingen absoluut gelijk is.

De meerdere of mindere kracht van den toon hangt eveneens af, van het karakter der trillingen, maar wordt weer op een andere wijze veroorzaakt dan de klankkleur.

De luchttrillingen brengen ons dus de volgende tegenstellingen:

[p. 45]

het hooge of lage van een toon (hoogte), het sterke of zwakke, (kracht) en het scherpe of weeke (klankkleur).

De tijdduur brengt ons de tegenstelling: het lange of korte, waardoor ook het zware of lichte karakter der tonen ontstaat.

Het spreekt van zelf, dat men in deze groote verscheidenheid orde moet scheppen, wil men de toonkunst niet door groote wanorde in een onverstaanbare chaos van tonen zien ontaarden, en dit ordenen en regelen van al die tegenstellingen wordt gedaan door de Rythmiek.

Vincent d'Indy geeft in zijn ‘Cours de composition musicale’ de volgende definitie: ‘Le rythme, c'est l'ordre et la proportion dans l'espace et dans le temps.’ en wat verder schrijft hij: ‘Pour la musique, art de succession, basée sur la division esthétique du temps, le rythme est plus spécialement: l'ordre et la proportion dans le temps.’ Het is zeker, dat de rythmiek op de eerste plaats verband houdt met de verhoudingen in den tijd, maar dit sluit volstrekt niet uit, dat de invloed der Rythmiek zich ook moet uitstrekken over de tegenstellingen en verhoudingen, die meer door de lucht geschapen worden. Zoo is de tegenstelling van sterk en zwak, scherp en week, hoog en laag even goed rythmisch te behandelen, als lang en kort, al moeten wij toegeven, dat hun effecten veel gemakkelijker te begrijpen zijn, dan die der langere of kortere duur der tonen.

Bestudeeren wij dus eerst de rythmiek van den tijd.

Gaat men het tikken van een uurwerk aandachtig na, dan zal men spoedig geneigd zijn, aan een op bepaalden tijd terugkeerenden tel meer nadruk te geven dan op de andere, b.v. stellen wij dat tikken voor als volgt:

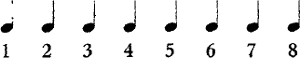
dan zullen wij onwillekeurig deze tellen gaan rangschikken in groepen van twee of drie tellen. De eerste van iedere groep lijkt ons zwaarder, omdat wij daarop steunen en de andere tellen voelen wij lichter aan, omdat die ons, als 't ware, weer opheffen naar het volgende steunpunt. Wij zouden zelfs geneigd kunnen zijn, om de eerste tel van iedere groep sterker te noemen dan de andere, wat echter een verkeerde opvatting zou zijn, daar wij toch weten, dat alle tellen precies even sterk zijn. Dat is trouwens zeer gemakkelijk te bewijzen. Verdeelen wij bovengenoemde reeks tellen in groepen van twee, dan zouden: 1, 3, 5 en 7 het steunpunt hebben, terwijl bij een driedeelige groepeering 1, 4 en 7 het sterkst zouden lijken. Daar de tikken elkaar in beide gevallen in absoluut dezelfde volgorde opgevolgd zijn, is 't onmogelijk, dat in één geval 1, 3, 5 en 7 en in een ander geval 1, 4 en 7 het sterkst zouden

[p. 46]

zijn. Deze proef bewijst tevens, dat de rythmiek door den kunstenaar (hetzij scheppend of uitvoerend) zelf gevoeld en dus tot uiting gebracht moet worden en zich dus niet uit zich zelf opdringt. Een proeve met verdeeling in grootere groepen is overbodig, daar 4 tellen 2 × 2 zijn, 5 tellen 3 + 2, 6 tellen 2 × 3 of 3 × 2 enz. Het is ook absoluut niet noodig, dat de steunpunten elkaar op geregelde tijdsafstanden opvolgen, wat het Gregoriaansch bewijst in haar massa's heerlijke, fijn gerythmeerde melodieën.

Men onderscheidt dus twee soorten rythme, n.m. de verdeeling in elkaar gelijke en in niet aan elkaar gelijke groepen.

In 't eerste geval noemt men dat gebonden, in het tweede vrij rythme. Voorloopig houden wij ons echter bezig met de eerste soort.

Wij hebben gezien, dat de eerste tel van iedere groep een zwaarder karakter heeft dan de andere. Luisteren wij nog eens aandachtig dan lijken ons de lichte tellen eenigszins afgestooten (dus korter), als bereiden zij met een of meer lichte sprongen het steunpunt voor, zooals men b.v. den voet opheft, om hem weer neer te kunnen zetten. Daaruit volgt dus, dat een rythmische figuur moet bestaan uit twee deelen, n.m. de beweging (opheffing) en de rust (het neerzetten). Dit neerzetten kan definitief zijn en is dan de rust na de beweging, het kan ook voorloopig zijn en is dan eigenlijk maar een steunpunt, om met een nieuwe beweging te kunnen beginnen. Het spreekt vanzelf, dat een rythmische figuur (niet te verwarren met een groep) begint met een beweging (arsis) en eindigt met een neerdaling (thesis).

De arsis heeft dus een bewegelijk, versnellend karakter, terwijl de thesis meer een rustiger, dus vertragend karakter bezit. Wij hebben nu nog maar alleen gesproken van een arsis en thesis, die in tijdduur aan elkaar gelijk zijn, dus een rythmische verdeeling in groepen van twee tellen. Luisteren wij nu aandachtig naar een verdeeling in driedeelige groepen, dan zal de derde tel het karakter van de opheffing en de eerste tel het karakter van den neerslag krijgen, terwijl de tweede tel ons aandoet als een uitvloeisel van den eersten of als een voorbereiding van den derden: b.v.

Laten wij nu in iedere groep de tweede tel in den eersten vervloeien, dan is er geen twijfel meer mogelijk omtrent den vorm der rythmische figuur: b.v.

[p. 47]

De langere tel 1-2 neemt onmiddellijk het karakter aan van het steunpunt en de korte derde tel heeft het uitgesproken karakter van de opheffing.

Wij mogen dus concludeeren, dat, bij een tegenstelling van een langen en een korten tel, de langere steeds het steun- of rustpunt wordt en de kortere steeds de beweging uitdrukt. Om dus een reeks tellen goed te rythmeeren, moet men ze eerst verdeelen in aan elkaar gelijke groepen (metrische verdeeling) en daarna in rythmische figuren: b.v.

Het teeken geeft de rythmische figuur, de strepen | | de groep aan. Uit dit voorbeeld blijkt ook duidelijk het onderscheid tusschen de rythmische en metrische behandeling van een reeks tellen of tonen, waarover in een volgend artikel.

Nijmegen.

WILLEM VAN KALMTHOUT.