Nederlandse Taalkunde. Jaargang 1
(1996)– [tijdschrift] Nederlandse taalkunde–
[pagina 177]
| ||||||||||||||||||||||||||||||||||||||||||||
[Nummer 3]* Rekenen met richting
| ||||||||||||||||||||||||||||||||||||||||||||
1 InleidingIn de semantiek van voorzetsels en andere ruimtelijke uitdrukkingen speelt het begrip richting op verschillende manieren een belangrijke rol. Zo geeft in (1) de keuze voor een bepaald voorzetsel aan dat men de programmagids in een zekere richting ten opzichte van de televisie (het referentieobject) moet zoeken:
Dezelfde richtingen zien we terug bij bijwoorden die een beweging aangeven:
| ||||||||||||||||||||||||||||||||||||||||||||
[pagina 178]
| ||||||||||||||||||||||||||||||||||||||||||||
Beweging in of uit een bepaalde richting, uitgedrukt met behulp van de voorzetsels naar en van, is op hetzelfde systeem gebaseerd:
Er is veel onderzoek verricht naar de wijze waarop richtingen bepaald worden, vooral in het Engels (bijvoorbeeld Fillmore 1971, Clark 1973, Miller en Johnson-Laird 1976, Herskovits 1986), maar ook in zulke uiteenlopende talen als het Duits (Lang 1991), het Frans (Vandeloise 1991), het Haussa (Hill 1982) en het Tzeltal (Levinson en Brown 1990). Daardoor weten we dat er allerlei manieren bestaan om richtingen te bepalen. De absolute richtingen maken gebruiken van kenmerken van de natuurlijke omgeving zoals de zwaartekracht (boven en onder), de wind of de zon (noord, oost, zuid, west) en bergen (bergop, bergaf) of rivieren (stroomopwaarts, stroomafwaarts). De relatieve richtingen zijn gebaseerd op eigenschappen van het referentieobject zelf (zoals bij de voor- en achterkant van een auto). De deiktische richtingen maken gebruik van een gezichtspunt (zoals bij de voor- en achter en linker- en rechterkant van een boom op een foto). In de literatuur is echter minder aandacht besteed aan de algemene eigenschappen van de richtingsuitdrukkingen, los van hun fysische of perceptuele oorsprong. Het doel van dit artikel is om (op een informele manier) aan te tonen dat al deze richtingen, hoe verschillend ook, deel uitmaken van één algemeen richtingssysteem dat gebaseerd is op het wiskundige vector-begrip. Om de eigenschappen van dat systeem te bepalen zal vooral gekeken worden naar verschijnselen die in de literatuur niet zo'n belangrijke rol spelen: bepalingen als recht en schuin en precies en ongeveer, samenstellingen als linksboven en noordoost en vergelijkingen als meer boven dan naast. Deze uitdrukkingen laten zien dat we in het Nederlands niet alleen de vertrouwde hoofdrichtingen (zoals voor, boven en noord) kunnen aanduiden maar ook ‘tussenliggende’ richtingen (schuin voor, linksboven en noordoost). Zo'n tussenliggende richting kan, als we gebruik maken van vectoren, worden gezien als de som van twee hoofdrichtingen. Er wordt als het ware ‘gerekend’ met richting. | ||||||||||||||||||||||||||||||||||||||||||||
2 Assen en vectorenRichtingen kunnen worden weergegeven in een assenstelsel (Figuur 1). De oorsprong van het assenstelsel (het punt waar de drie assen elkaar loodrecht snijden) wordt bepaald door het referentieobject (zoals de televisie in (1), die hier voor het gemak als een punt wordt opgevat). Omdat elke as twee helften heeft, zijn er in totaal zes verschillende ‘halfassen’. Assen en halfassen zullen worden aangeduid met hoofdletters (bijv. de LINKS-RECHTS-as of de BOVEN-as). De meeste voorzet- | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 179]
| ||||||||||||||||||||||||||||||||||||||||||||
sels in (1) en bijwoorden in (2) corresponderen met een halfas (bijv. boven en omhoog met de BOVEN-as); alleen naast en opzij horen bij de hele LINKS-RECHTS-as. 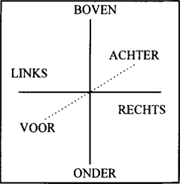
Figuur 1: Assenstelsel met zes basisrichtingen
Het assenstelsel is een ruimtelijk raamwerk waarin posities kunnen worden vastgelegd. In de wiskunde gebeurt dat wel door middel van een vector, een pijl die vanuit de oorsprong (het referentiepunt) een positie aanduidt, zoals in de figuren 2a en 2b. De plaatjes zijn voor het gemak twee-dimensionale ‘aanzichten’ (voor-, bovenen zijaanzichten). 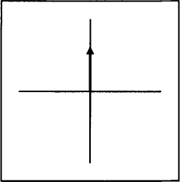
Figuur 2a
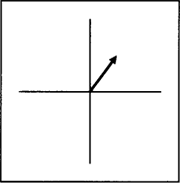
Figuur 2b
Een vector heeft twee eigenschappen, een lengte en een richting, die samen eenduidig een positie vastleggen. Een vector is dus geen richting, maar kan wel gebruikt worden om een richting aan te geven. In het voorbeeld van de televisie en het programmablad in (1) is de vector een soort denkbeeldige arm met wijsvinger die uit de als oorsprong fungerende televisie wijst naar de plaats van de televisiegids. De rol die de televisie hier als oorsprong of referentiepunt speelt, wordt in de literatuur ook wel aangeduid als ground (Talmy 1978) of landmark (Langacker 1986). Behalve plaats moet ook beweging in het assenstelsel worden aangegeven en daarvoor is één vector niet voldoende. Beweging is verandering van plaats en daarom kan een beweging globaal weergegeven worden door een reeks van posities (dus vectoren) die tijdens de beweging op verschillende tijdstippen worden ingenomen, als een soort film (zie ook Hawkins 1984 en Langacker 1986) (Figuur 3). | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 180]
| ||||||||||||||||||||||||||||||||||||||||||||
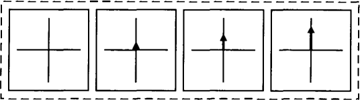
Figuur 3a: naar boven
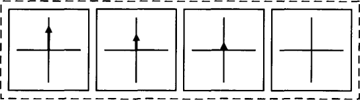
Figuur 3b: van boven
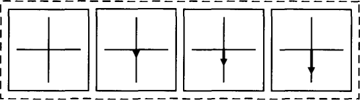
Figuur 3c: naar beneden
In figuur 3a is sprake van een beweging omhoog (‘naar boven’) vanuit de oorsprong. Wanneer de volgorde van de vectoren in figuur 3a wordt omgekeerd resulteert de beweging in figuur 3b (‘van boven’). Wanneer de vectoren zelf worden omgekeerd (dat wil zeggen: 180o gedraaid om de oorsprong) krijgen we figuur 3c, een beweging omlaag (‘naar beneden’). Zo'n reeks van posities zal ik in navolging van de literatuur een pad noemen (Jackendoff 1983). Het verschil tussen naar boven en van boven laat zien dat voor het representeren van paden niet met één vector volstaan kan worden. Een pad is een samengesteld begrip, wat ook blijkt uit het feit dat veel pad-uitdrukkingen zijn afgeleid van plaats-uitdrukkingen (naar boven, van links, vooruit, omlaag, linksaf). Dat is ook duidelijk als we het pad willen aangeven dat wordt uitgedrukt door de zin Jan loopt om het huis heen, waar vectoren vanuit het huis naar Jans wisselende posities wijzen (Figuur 4). 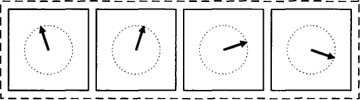
Figuur 4: Rondgaande beweging
Hier blijft in tegenstelling tot de bewegingen in figuur 3a tot en met 3c, de lengte van de vectoren constant, maar verandert de richting. Rondgaande bewegingen spe- | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 181]
| ||||||||||||||||||||||||||||||||||||||||||||
len verder in dit artikel geen rol, omdat we ons concentreren op bewegingen in één richting. Wat nu nog ontbreekt is een manier om de richting van een vector binnen het assenstelsel te karakteriseren. Voor de vector in figuur 2a, die precies op de BOVEN-as ligt, is dat niet moeilijk, maar de status van de vector in figuur 2b, die niet op een van de assen ligt, maar ertussenin, is niet direct duidelijk. Deze vector moet daarom worden ontleed in twee vectoren, één op de BOVEN-as en één loodrecht daarop op de horizontale as (Figuur 5). 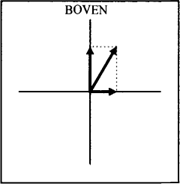
Figuur 5: Ontbinding van een vector in twee componenten
Dit maakt het mogelijk om nauwkeuriger te bepalen in welke mate deze vector omhoog wijst. In het algemeen geldt dat elke vector in het assenstelsel kan worden ontleed in ‘basisvectoren’ op de assen van het stelsel (de componenten van die vector). Omgekeerd kan de ‘scheve’ vector in figuur 5 ook worden beschouwd als de som (de zogenaamde vectorsom) van een verticale en een horizontale basisvector. De verzameling van vectoren in het assenstelsel vormt namelijk een rekenkundig stelsel met optelling en vermenigvuldiging. Er kan dus daadwerkelijk gerekend worden met vectoren, zij het dat de rekenobjecten hier niet getalsmatig zijn maar meetkundig. Een assenstelsel met vectoren verschaft dus niet alleen de bekende zes richtingen (boven, onder, voor, achter, links, rechts), maar ook ‘samengestelde richtingen’ die het resultaat zijn van een optelling van basisrichtingen. De vraag is nu: komen zulke samengestelde richtingen ook daadwerkelijk voor in het Nederlands? De volgende paragraaf zal duidelijk maken dat er goede redenen zijn om richtingen inderdaad te ontleden in componenten. | ||||||||||||||||||||||||||||||||||||||||||||
3 Samengestelde richtingDe voorzetselgroep achter de camera in (4) kan worden gebruikt om verschillende gebieden van de ruimte aan te duiden:
De omvang van dat gebied is niet in elk voorbeeld hetzelfde, maar varieert zoals aangegeven in figuur 6a, 6b en 6c (alle bovenaanzichten). | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 182]
| ||||||||||||||||||||||||||||||||||||||||||||

Figuur 6a
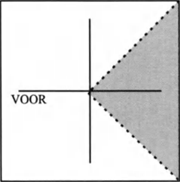
Figuur 6b

Figuur 6c
Zin (4a) zal normaal gesproken zo worden opgevat dat de regisseur zich ergens bevindt op een lijn die precies achter de camera ligt, zodat hij voor de actrice vóór de camera onzichtbaar is. Het gebied achter de camera in (4b) wordt ruimer opgevat, als een uitwaaierend gebied, want de cameraman kan ook als hij schuin achter de camera staat zijn beeldschermpje nog goed zien. De crew in (4c) zal het gebied achter de camera weer wat ruimer hebben opgevat: het hele gebied aan één kant van de LINKS-RECHTS-as door de camera. Er blijkt dus een zekere variatie te zijn in de interpretatie van voorzetsels, die sterk afhankelijk is van de situatie, de aard van het referentieobject (hier de camera met voorop een lens en achterop de knoppen) en van de bedoelingen van de spreker. In (4a) is voor de spreker het gebied achter de camera alleen van belang voor zover de regisseur daar aan het oog van de actrice onttrokken is. In (4b) betekent achter de camera voor de spreker zoiets als ‘in visueel contact met de achterzijde van de camera’. De interpretatie van (4c) vooronderstelt een eenvoudige opdeling van de ‘set’ in twee gebieden: voor de camera de acteurs en achter de camera de crew. Variatie is er ook in de richting die wordt aangeduid door omhoog. Een raket die omhoog stijgt kan recht omhoog gaan langs de BOVEN-as, enigzins schuin daarvan afwijken of onder een hele flauwe helling het luchtruim kiezen. Die drie mogelijkheden zijn in Figuur 7a, b en c aangegeven. 
Figuur 7a
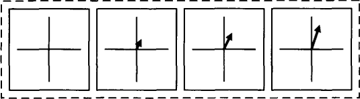
Figuur 7b
| ||||||||||||||||||||||||||||||||||||||||||||
[pagina 183]
| ||||||||||||||||||||||||||||||||||||||||||||
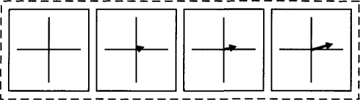
Figuur 7c
De gebruiksmogelijkheden van omhoog kunnen onderscheiden worden door de vectoren in figuur 7 te ondeden in twee basisvectoren, één in de BOVEN-as en eventueel een vector in het horizontale vlak. Dan is duidelijk zichtbaar wat de varianten van omhoog gemeen hebben: een component op de BOVEN-as. De strikte variant a eist dat de hele vector op de BOVEN-as ligt, zonder horizontale ‘rest-component’. Variant b eist dat de component op de BOVEN-as groter is dan de andere component. De hoek die de vector met de BOVEN-as maakt moet dan dus kleiner zijn dan 45o. Voor variant c is het voldoende dat er een component op de BOVEN-as is, hoe klein ook. Op dezelfde manieren kunnen de gebieden van achter de camera in (4) worden gedefinieerd:
Een voorzetselgroep als achter de camera kan dus semantisch worden opgevat als een verzameling vectoren, namelijk die vectoren die aan een bepaalde voorwaarde voldoen, en zo'n verzameling vormt een gebied zoals in de figuren in 6 is aangegeven. De voorbeelden laten zien dat verschillende gebruiksvormen van een richtingsuit-drukking pas duidelijk kunnen worden onderscheiden als we de aangeduide richting als een vectorsom analyseren. Er zijn ook bepalingen om de ligging van een vector ten opzichte van een as expliciet te maken:
Het gebruik van de woorden recht en schuin is niet beperkt tot voorzetsels en bijwoorden van richting, zoals de volgende voorbeelden laten zien:
Een object kan alleen recht of schuin zijn ten opzichte van een referentie-as of -kader. De toren in (7a) is recht of schuin ten opzichte van de verticale as van de | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 184]
| ||||||||||||||||||||||||||||||||||||||||||||
zwaartekracht (of de horizontale as van de horizon); het pad in (7b) is recht of schuin ten opzichte van het rechthoekig kader van de tuin; de oversteek in (7c) is recht of schuin ten opzichte van de straat. Op dezelfde manieren zijn de richtingsbepalingen recht en schuin in (6) relatieve noties: ze hebben betrekking op de richting van een vector in een assenstelsel. De ontbinding van een vector in componenten maakt het gemakkelijk om de betekenis van recht en schuin te specificeren. De vector in figuur 8a geeft de positie aan die kan worden gekarakteriseerd als recht achter de camera, de vector in figuur 8b illustreert schuin achter de camera. 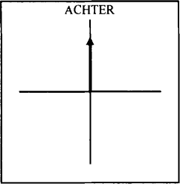
Figuur 8a: recht achter de camera
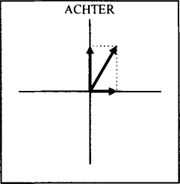
Figuur 8b: schuin achter de camera
Dus kunnen recht en schuin (ten opzichte van een as A) als volgt worden gedefinieerd:
In de zinnen in (6) zorgt het voorzetsel voor de specificatie van de A-as. Om in (7) de as te bepalen, hebben we kennis nodig van de normale richting van torens, tuinpaden en oversteken ten opzichte van de zwaartekracht, tuinen en straten, respectievelijk. Ook de woorden links en rechts kunnen naast hun zelfstandig gebruik als richtingsaanduidingen (links van de auto, rechts van het huis) als bepalingen worden gebruikt bij de voorzetsels voor, achter, boven en onder.
Deze voorbeelden laten steeds een combinatie zien van twee richtingen: het voorzetsel drukt een horizontale of verticale richting uit en de links/ rechts-bepaling geeft aan of die richting ‘overhelt’ naar links of rechts. De situatie van zin (9a) kan bijvoorbeeld worden voorgesteld zoals in figuur 9. | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 185]
| ||||||||||||||||||||||||||||||||||||||||||||
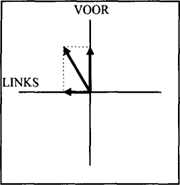
Figuur 9: links voor de auto
De auto vormt de oorsprong van het assenstelsel en de positie van de fietser wordt aangeduid door de som van de vector in de VOOR-as en de vector in de LINKS-as. De uitdrukkingen links voor de auto en rechts voor de auto duiden twee specifieke gevallen aan van de situatie die op een wat algemenere manier wordt beschreven door schuin voor de auto. Het is waarschijnlijk niet toevallig dat juist links en rechts de boven-onder- en voor-achter-richtingen bepalen en niet andersom. Behalve dat links en rechts adverbia zijn en voor, achter, boven en onder voorzetsels (en adverbia wel voorzetsels modificeren, maar niet andersom), kan ook een rol spelen dat het onderscheid tussen links en rechts secundair is ten opzichte van de door de voorzetsels gemaakte primaire onderscheidingen. Een andere klasse van bijwoorden die in het Nederlands worden gebruikt om een richting nader te kwalificeren heeft betrekking op nauwkeurigheid.
Deze bijwoorden worden ook gebruikt wanneer er een telwoord of tijdsaanduiding in het spel is:
Waar het bij deze bijwoorden om gaat is of er wel of niet een afwijking is van de gegeven waarde. In (11a) bijvoorbeeld kan de leeftijd van de firma gelijk zijn aan vijftig jaar, zonder enige afwijking (precies) of er kan sprake zijn van een kleine afwijking (ongeveer). Op dezelfde wijze kan er, zoals in figuur 10 aangegeven wordt, al dan niet een afwijking zijn tussen de vector die een satelliet of ongeluk lokaliseert ten opzichte van een als oorsprong gekozen stad of huis. In figuur 10a is de situatie weergegeven die correspondeert met exact boven en precies voor: de vector ligt op de as A en er is geen component op de as B loodrecht daarop. Figuur 10b laat een situatie zien die beschreven wordt door ongeveer boven en zowat voor: de vector bestaat uit een component op de as A en een kleine restcomponent op de as B die de afwijking aangeeft. In het algemeen zal zo'n ‘vaagheidsbepaling’ resulteren in een gebied om de as: exact boven Purmerend correspondeert met een lijn, maar ongeveer boven Purmerend met een uitwaaierend gebied (waar de BOVEN-as zelf misschien uit ontbreekt). | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 186]
| ||||||||||||||||||||||||||||||||||||||||||||
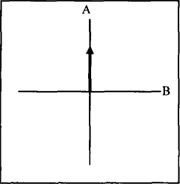
Figuur 10a
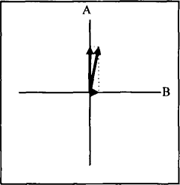
Figuur 10b
We hebben nu drie verschillende manieren gezien om de richting van een voorzetsel nader te bepalen: (i) met rechten schuin, (ii) met links en rechts, en (iii) met woorden als precies en ongeveer. De bijdrage die deze bepalingen leveren aan de hele richtingsuitdrukking kan alleen goed begrepen worden als we het samengestelde karakter van richtingen aannemen. Dit samengestelde karakter van richtingen blijkt ook uit de volgende constructie:
In (12a), bijvoorbeeld, wordt uitgedrukt dat het kogelgat zich op een zodanige positie bevindt ten opzichte van het hart dat boven en naast beide geschikte kwalificaties zijn, maar dat boven toch geschikter is dan naast. De positie van het kogelgat ten opzichte van het hart is gegeven als de som van twee vectoren, een langere op de BOVEN-as en een kortere op de LINKS-RECHTS-as (in Figuur 11 aangegeven met LR). 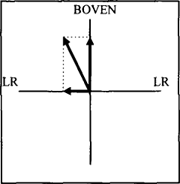
Figuur 11: meer boven dan naast
| ||||||||||||||||||||||||||||||||||||||||||||
4 WindrichtingenTot nu toe is in dit artikel de aandacht steeds uitgegaan naar voorzetsels en bijwoorden die betrekking hebben op de verticale as en op twee horizontale assen (VOOR-ACHTER en LINKS-RECHTS). Maar aanduidingen van plaats en bewe- | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 187]
| ||||||||||||||||||||||||||||||||||||||||||||
ging in het horizontale vlak kunnen ook gebruik maken van een assenstelsel dat gebaseerd is op de windstreken noord, zuid, oost en west. Hoewel de assen van dit stelsel op een heel andere manier gedefinieerd zijn dan de VOOR-ACHTER-as en LINKS-RECHTS-as, blijken ook windrichtingen een samengesteld karakter te hebben, wat duidelijk maakt dat er een algemeen systeem van richtingen is, met eigenschappen die onafhankelijk zijn van de natuurlijke of waarnemingsfactoren waarmee richtingen bepaald worden (zoals de werking van de zwaartekracht, de beweging van zon of wind of het perspectief van de spreker). De voorzetseluitdrukkingen en voorzetsels in (13) duiden een positie aan in een bepaalde windrichting:
De richtingsuitdrukkingen in (14) duiden een beweging aan in of uit een bepaalde windrichting:
Hoewel deze richtingen gebaseerd zijn op een ander gegeven dan richtingen als ‘voor’ en ‘links’ (namelijk op de opkomst en draaiing van de zon) blijken ze toch dezelfde eigenschappen te hebben. De windrichtingen kunnen worden voorgesteld in een twee-dimensionaal horizontaal assenstelsel met een NOORD-ZUID-as en een OOST-WEST-as (Figuur 12). 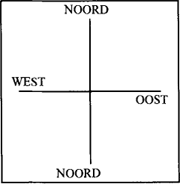
Figuur 12: Assenstelsel met windrichtingen
Plaatsen en bewegingen worden weer, net als bij de andere voorzetsels en bijwoorden, voorgesteld met behulp van vectoren. Een vector die zelf niet op een as ligt kan worden ontleed in twee vectoren op de assen (Figuur 13). | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 188]
| ||||||||||||||||||||||||||||||||||||||||||||
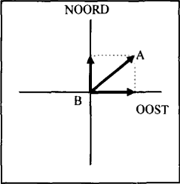
Figuur 13: Samenstelling van windrichtingen
Er zijn verschillende manieren om deze situatie te beschrijven:
In deze voorbeelden wordt gebruik gemaakt van het gegeven dat de plaats van punt A ten opzichte van punt B is gegeven met behulp van twee assen, de OOST-as, maar ook de NOORD-as. Deze uitdrukkingen staan in contrast met een ander type van richtingsuitdrukkingen die in maritieme en militaire kringen gebruikt worden voor de situatie in figuur 13:
(16a) veronderstelt dat de richtingen in het horizontale vlak als een cirkel verdeeld zijn in 360 graden en dat elke richting wordt gespecificeerd in termen van de hoek met de noordelijke richting. (16b) verdeelt de richtingen in twaalf uren zoals op een klok, waarbij het noorden met twaalf uur geïdentificeerd wordt. Ook hier kan de positie van A worden voorgesteld door middel van een vector in relatie tot een as (de NOORD-as), maar de relatie wordt in dit geval op een geheel andere wijze gespecificeerd, namelijk door middel van een speciaal meetsysteem dat de hoek specificeert tussen de vector en de referentieas. Merk op dat de richtingen in (16) niet zijn gebaseerd op speciale voorzetsels (voor, benoorden) of bijwoorden (omhoog, links), maar op nomina (graad, uur) met telwoorden. | ||||||||||||||||||||||||||||||||||||||||||||
5 ConclusieWe hebben gezien dat de betekenis van voorzetsels en bijwoorden van richting kan worden verklaard met behulp van vectoren in een assenstelsel. De assen geven alleen de tien basisrichtingen aan die corresponderen met de voorzetsels en bijwoorden van richting (boven/omhoog, onder/omlaag, voor(uit), achter(uit), links(af) en rechts (af), noord, oost, zuid, west). De vectoren zijn nodig om te verklaren waarom wij in het Nederlands ook richtingen kunnen aanduiden die ‘tussen’ de assen liggen. | ||||||||||||||||||||||||||||||||||||||||||||
[pagina 189]
| ||||||||||||||||||||||||||||||||||||||||||||
Hoewel dat op verschillende manieren kan (onder andere door bepalingen als recht en schuin en precies en ongeveer), is er één onderliggend principe: een richting (vector) kan worden samengesteld uit componenten op de hoofdrichtingen (de assen). Twee hoofdrichtingen kunnen bij elkaar worden opgeteld om een richting aan te duiden die niet met een bestaand woord correspondeert (zoals duidelijk te zien is in linksboven en noordoosten). Er wordt dus gerekend met richting in het Nederlands, waarbij we ‘rekenen’ moeten opvatten in de wiskundige zin van het uitvoeren van operaties op objecten, zoals we in de wiskunde ook kunnen rekenen met verzamelingen, waarheidswaarden of meetkundige figuren. In dit artikel is gekozen voor een informele behandeling van richtingsuitdrukkingen in het Nederlands. Allerlei interessante empirische en theoretische kwesties zijn buiten beschouwing gebleven. Omdat alle aandacht uitging naar het begrip richting is een ander belangrijk aspect van de vectoren, hun lengte, buiten beschouwing gebleven, terwijl het Nederlands juist een grote rijkdom aan bepalingen kent die de lengte van een vector kunnen specificeren (twee meter/vlak/dicht/ver/heel hoog boven de tafel). Over die constructies kan de lezer meer vinden in Zwarts (1994). Bovendien wordt in dat artikel explicieter en formeler dan hier duidelijk gemaakt hoe we ons de interpretatie van voorzetsels en hun bepalingen in termen van vectoren moeten voorstellen. Het is niet waarschijnlijk dat de hier gepresenteerde vector-benadering beperkt is tot richtingsuitdrukkingen in het Nederlands. Het vector-concept heeft een veel ruimere toepasbaarheid in het ruimtelijke domein, zowel met betrekking tot natuurlijke taal als cognitie. Zo zijn de visuele 3D-modellen van Marr (1982), die ruimtelijke objecten op een perspectief-neutrale manier mentaal representeren, gebaseerd op vectoren die de lengte en oriëntatie van assen aangeven. Levinson (1992) past deze theorie toe op lokatieve uitdrukkingen in het Tzeltal. We kunnen vectoren dan zien als de bouwstenen van onze cognitieve organisatie van de ruimte die zich weerspiegelt in bepaalde uitdrukkingen van het Nederlands en andere talen. | ||||||||||||||||||||||||||||||||||||||||||||
Bibliografie
| ||||||||||||||||||||||||||||||||||||||||||||
[pagina 190]
| ||||||||||||||||||||||||||||||||||||||||||||
|
|

