De Hollandsche Lelie. Jaargang 29

Hoofdartikel
't Rekenen op school.

't Is vanouds geweest de glorie der schoolmeesters goede rekenmeesters te zijn. De ingewikkeldste en vaak onzinnige rekenkunstige voorstellen, in de onbegrijpelijkste taal geschreven, losten ze op. Die vraagstukken besloegen menigmaal een halve bladzij druks en waren geheele verhalen. De gegevens er uit te halen, noodig en onmisbaar voor de oplossing, was een hersenafmattend werk. Hoe langer de opgaven, hoe mooier men ze vond. De oplossingen, uitvoerige en vaak omslachtige redeneeringen, waren geheele verhandelingen, compleete opstellen. Dit is wel wat veranderd, vooral de opgaven moeten, hoe ingewikkeld het vraagstuk ook is, zoo beknopt en duidelijk mogelijk zijn. Maar nog altijd heeft men aparte ‘sommen’ voor dat apart soort volk, dat men nog veelal bestempelt met den naam van schoolmeesters. Op 't onderwijzers-examen wordt afzonderlijk bij 't schriftelijk gedeelte opgegeven een vier- of vijftal ‘sommen’ (= rekenkundige vraagstukken), die uitsluitend door schoolmeesters te maken zijn, behalve één ervan uit de Vormleer (= Aanschouwelijke Meetkunde),

[p. 690]

welke opgave door iemand, die Wiskunde, en in dit bijzonder geval Meetkunde, geleerd heeft, meestal zonder moeite wordt uitgewerkt. Het dresseeren van de jongelui voor het juist uitvoeren van deze krachttoeren duurt vier jaar, twee uur per week. Men kan dit oplossen slechts gedeeltelijk leeren door de toepassing van de theorie der rekenkunde; het beantwoorden en uitwerken dezer vraagstukken heet dan ook zeer eigenaardig practisch rekenen, hoewel er zeker niets meer onpractisch te bedenken is en het daarom juister gekarakteriseerd zou worden door den naam onpractisch rekenen. - Maar, ziet U, 't is in tegenstelling met de theorie, dus: practisch. - Er is ook, ik mag dit ter wille van de waarheid niet verzwijgen, er is ook wel eens een practisch vraagstuk bij, d.w.z. een vraagstuk dat in 't leven voorkomt. En in elk geval moet bij de oplossing meestal, bijna altijd, gecijferd worden, en dit is toch ongetwijfeld practisch.

Misschien denkt de ongeloovige lezer(es), dat ik overdrijf of maar wat vertel, maar hebt U nooit eens in de krant in April - 1 April wordt het schriftelijk examen doorgaans afgenomen - de rekenkundige opgaven nagezien? Of hebt U dan gemeend dat het een Aprilgrap was? Dan was U mis, 't was wel April, maar een grap was het niet. Ik zal maar eens eenige overschrijven voor den voet weg.

Onderwijzers-examen te Haarlem (1913).
1½ uur.

1. Het jaarlijksch inkomen van A staat tot dat van B als 2:3. Hunne uitgaven staan tot elkaar als 7:10. Als A nu jaarlijks ƒ 80 bespaart en B ƒ 200, hoeveel bedraagt dan het jaarlijksch inkomen van A?

2. Een wandelaar vertrekt om 9.40 uit A en komt 11.25 te B aan. Indien hij elke 3 minuten 10 M. meer had afgelegd, zou hij 5 minuten eerder zijn aangekomen. Hoe lang is de weg van A naar B?

3. Iemand heeft op 1 Januari 1910 een kapitaal uitgezet op samengestelden interest à 4 % 's jaars. Op 1 Januari 1911 neemt hij er ƒ 1000 af, welk bedrag hij er op 1 Januari 1912 weer bijvoegt. Hoeveel zal hij nu op 1 Januari 1913 minder bezitten dan wanneer hij zijn kapitaal onveranderd had gelaten?

4. Een aannemer verbindt zich om in 75 dagen een terrein op te hoogen. Aanvankelijk stelt hij daartoe 120 werklieden aan 't werk en als ⅗ van het terrein is opgehoogd, neemt hij nog 40 man in dienst. Als het werk nu op tijd gereed is, hoeveel dagen hebben dan deze 40 werklieden er aan geholpen?

5. De uitwendige vorm van een houten bakje is een kubus, waarvan de ribbe 12 c.M. is. De bodem is 2 c.M. en de opstaande wanden zijn 1 c.M. dik. Hoe zwaar is dat bakje, als het soortelijk gewicht van het hout 0,75 is?

(Wie ze eens wil oplossen, ziehier de antwoorden: no. 1: ƒ 1200; no. 2: 7 K.M.; no. 3: ƒ 41,60; no. 4: 25 dagen; no. 5: 0,546 K.G.).

Ik heb deze vraagstukken niet uitgezocht en geef, om te laten zien dat ze elders gelijksoortig zijn, nog eenige opgaven.

Onderwijzers-examens te Breda, Arnhem, Zutphen, Venlo. (1913)^*)
2 uur.

1. Van twee kapitalen, samen groot ƒ 5500, heeft het eerste 10 maanden, en het tweede 8 maanden uitgestaan. Aan rente hebben zij samen ƒ 186 opgebracht. Als het eerste kapitaal tegen 5% uitstond, en het tweede met zijn interest ƒ 3811 bedroeg, tegen hoeveel percent 's jaars heeft dan het laatste uitgestaan?

2. Een winkelier verkoopt het 4/9 van een partij koopwaren tegen ƒ 1,46 per K.G., en moet de rest tegen ƒ 1,42 per K.G. van de hand doen. Op elk der twee genoemde deelen van de partij heeft hij ƒ 96 gewonnen. Bereken den inkoopsprijs der geheele partij.

3. (Verbazend practisch, G.) Een zak bevat een zekere geldsom in guldens, kwartjes en dubbeltjes, in 't geheel 420 geldstukken. Neemt men er het vijfde deel der guldens, het vijfde deel der kwartjes en de helft der dubbeltjes uit, dan blijft er nog ¾ der geheele geldsom over. Als de gezamenlijke waarde van alle kwartjes het dubbele is van die der dubbeltjes, hoeveel geldstukken van iedere soort zijn er dan in dien zak?

4. Het grondvlak van een rechthoekig parallelepipedum is 12 c.M. lang en 9 c.M. breed. Verdeelt men het lichaam in vier gelijke deelen door een vlak, gaande door twee opstaande ribben, en een tweede vlak, evenwijdig met het grondvlak, dan bedraagt het geheele oppervlak van een der deelen 5,94 d.M². Druk het totale oppervlak van het oorspronkelijk lichaam in vierkante meters uit.

*) In deze steden werden dezelfde vijf vraagstukken opgegeven.

[p. 691]

5. Een schip volbracht een zeereis in



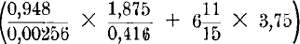uren, en de terugreis in ⅞ van dien tijd. Druk den duur der heenreis in weken, dagen en uren uit, en leid uit de verkregen uitkomst den duur der terugreis af, eveneens uitgedrukt in weken, dagen en uren. (De geheele bewerking inleveren).

[De antwoorden, voor de(n) liefhebber(ster), zijn respectievelijk: 4½%; ƒ 680,40; 60 guld., 160 kw. en 200 dubb.; 0,135 M².; In 9 w. 6 d. 23 u., in 8 w. 5 d. 5⅛ u.].

Opm. Men moet weten dat de vraagstukken niet algebraïsch mogen worden opgelost, zooals b.v. no. 3, dat met vergelijkingen gemakkelijk wordt gevonden.

No. 5 ziet er zeer onpractisch uit, doch dit wordt eenigermate vergoed doordat het vraagstuk aanleiding geeft tot een ingewikkelde becijfering, die een onderwijzer(es) accuraat behoort te kunnen maken. Men had hetzelfde doel bereikt met de opgave:

Herleid tot weken, dagen en uren: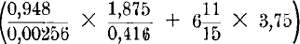



uur, en druk het ⅞ deel ervan ook in die tijdsdeelen uit.

Zooals het voorstel is opgegeven, lijkt het een weinig op de rekenkunstige vraagstukken uit de 16e en 17e eeuw.

De vraagstukken op het examen voor de hoofdakte zijn natuurlijk nog moeilijker, ingewikkelder; voor den oningewijde lijken zij soms onoplosbare raadsels.

Nu wil ik aan zulke ‘sommen’ niet alle waarde ontzeggen. 't Spreekt immers vanzelf dat ze tot denken dwingen. Maar dit zoogenaamd practisch rekenen is bij uitstek onpractisch, immers komen de meeste veronderstelde gevallen niet voor of niet voor in denzelfden vorm als in de ‘sommen.’ (Altijd met de vroeger reeds gemaakte exceptie, dat wel eens vraagstukken worden opgegeven aan de praktijk, het leven, de maatschappij ontleend.) Er is geen andere menschensoort op de wereld die dergelijke onpractische vraagstukken oplost. Zij worden uitsluitend bedacht voor de onderwijzers. Voorzeker, 't is een nuttige sport, maar toch minder vormend, ontwikkelend dan schaken, en 't staat bijna even ver buiten de werkelijkheid van 't maatschappelijk leven. Waarom laat men de onderwijzers, evenals alle menschen die wat meer ontwikkeling verwerven, op de scholen na het gewoon lager onderwijs, geen wiskunde leeren en examineert hen daarin? Dit zou practisch zijn in tweeërlei opzicht: 1^o. het leert logisch denken, 2^o. het is te gebruiken in 't leven. Wellicht vraagt menig(e) lezer(es) verbaasd: Leeren de onderwijzers dan geen wiskunde, d.i. meetkunde en algebra? Ja, op vele opleidingsinrichtingen wordt er wel iets aan gedaan, op vele andere echter niets. Voor 't examen is 't niet noodig. Enkel rekenen en wat zoogenaamde vormleer, dat het best verklaard wordt door de omschrijving: aanschouwelijke meetkunde. Dit is noodig voor 't oplossen van n^o. 5, opgegeven te Haarlem, en n^o. 4, gevraagd in de andere bovengemelde steden. Wel staat het den onderwijzers vrij een afzonderlijk - moeilijk! - examen af te leggen in de wiskunde (lagere akte), maar dit doen uit den aard der zaak zeer weinigen, het gros, 95%, heeft geen examen gedaan in dit vak en zeer velen weten van meetkunde en algebra weinig of niets.

Hoe weinig wiskunde er in die practische rekenkundige vraagstukken zit (lees voor practische liever onpractische) blijkt het best uit de treffende omstandigheid dat hij (zij) die geen moeite heeft om meetkunde en algebra te leeren, met de grootste inspanning soms niet in staat is een rekenkundig vraagstuk op te lossen, als voor onderwijzers is gefabriceerd.

Zoo staat dus, wat de dressuur voor 't ‘sommen’-maken betreft, de opleiding van den onderwijzer, wiens roeping het is de jeugd tot het leven en de maatschappij voor te bereiden, buiten de werkelijkheid. De nadeelige gevolgen blijven niet uit, kunnen niet uitblijven. Wie es in den Wald hineinschallt, so schallt es wieder heraus. De behoefte van den goeden onderwijzer is zich aan de jeugd te geven; wat hij is, kent, kan, weet, gevoelt, tracht hij de jeugd te geven. Hij zit vol gekunstelde rekenkunde en als hij nu dit vak onderwijst en de kindertjes de eerste handgrepen der hoofdbewerkingen kunnen uitvoeren, ja, dikwijls reeds gedurende het aanleeren dezer operaties, worden er ‘sommen’ gemaakt, d.i. rekenkundige voorstellen opgelost.

In de vijfde en de zesde klas (= leerjaar) moeten ze op vele scholen beredeneerd worden opgelost. De oplossing is dan een samenhangende, min of meer logische redeneering, een opstelletje. Gelukkig wordt dit thans niet veel meer gedaan. Er steekt natuurlijk wel nut in, maar 't blijkt voor kinderen veel te moeilijk te zijn. Kinderen zijn nog niet

[p. 692]

logisch; men bemerkt dit het best bij 't onderwijs in de meetkunde. (Hoeveel moeite kost het niet om ze een logisch bewijs te leeren snappen en daarna zelf te laten geven! En dit geschiedt bij veel oudere leerlingen dan die van 't vijfde en zesde leerjaar.) Zoo groeien de sommen in moeilijkheid, en als de kindertjes er maar voor geschikt waren, zouden de methodes, de rekenboekjes, hen met hun twaalfde jaar tot rekenmeesters maken. Die methodes zijn kunstrijke of liever kunstige bedenksels. Als men ze gelooven wou, want de bedoeling wordt uitvoerig uitgelegd in groote Handleidingen voor den Onderwijzer, kost het volstrekt geen moeite de kindertjes alles te leeren wat de boekjes bevatten, zonder moeite, want het gaat langs lijnen van geleidelijkheid, o zoo langzaam vooruit schijnbaar, maar men staat verbaasd over de vraagstukken die kinderen van 11 en 12 jaar dan toch met en tengevolge van al die langzame geleidelijkheid krijgen op te lossen. De zoogenaamd beste rekenmethodes zijn gewoonlijk de moeilijkste, d.w.z. ze zijn zeer geleidelijk maar brengen de leerlingen het verst. Met de grootste zorg en de krachtigste overtuiging wordt het den onderwijzer in de Handleiding voorgehouden dat de leerlingen de vraagstukken moeten kunnen maken, mits hij zich maar houdt aan de leiding. Niet te verwonderen is het, dat onder en door al dat vraagstukken oplossen (deze vraagstukken zijn vaak zoogenaamde denkoefeningen, een mooi woord voor een leelijk ding) de leerlingen het cijferen verleeren, indien ze dit ten minste gekend hebben. En cijferen is toch de hoofdzaak! Wat er in 't dagelijksch leven voor den gewonen mensch te berekenen valt, komt eenvoudig neer op cijferen of uit het hoofd rekenen. Een eerste eisch dien het leven aan den mensch stelt, is dat hij accuraat cijfert met eenvoudige, meestal kleine getallen. Dit moet en kan de school aan de jeugd tot twaalf jaar leeren. Dit moest dus de taak der school zijn. Maar al sommen-makende schoot soms het cijferen er grootendeels of te veel bij in.

Zoo ontstond er reactie: Weg met alle rekenkundige vraagstukken, met alle beredeneerde oplossingen, weg met dikke handleidingen, die den onderwijzer binden en belemmeren, weg met geleerde methodes! Laten we de jeugd leeren cijferen!

Gelukkig dat die reactie gekomen is. Peper, Thijssen e.a. hebben ook sommenboeken gegeven, maar deze ‘sommen’ zijn eenvoudig, geen ellenlange uitleggingen zijn noodig, 't is gesneden koek, de kinderen kunnen er zoo maar op aanvallen. En ziet ze nu aan den slag gaan! Welk een ijver, welk een lust! Want een kind is graag bezig, het wil werken, iets doen. Nu cijfert het kind en kan het als 't van school gaat.

Deze nieuwe beweging: cijferen leeren en geen vraagstukjes oplossen, is thans bezig de gewone lagere school van de geleerde methodes te bevrijden, zij bewerkt meteen de emancipatie van den onderwijzer, die nu zelf, zonder handleiding, onderwijst. Natuurlijk is deze reactie overdreven, elke reactie gaat te ver. Maar deze richting is beter dan de andere en langzaam-aan zullen beide samengaan langs een lijn, die middendoor loopt tusschen beide en dan zal 't goed zijn.

Deze nieuwe richting vindt men echter alleen op de gewone volksschool. Nog is deze hervorming niet doorgedrongen tot de scholen voorbereidende tot H.B.S. en Gymn., evenmin tot de scholen voor M.U.L.O. Hier vieren de rekenkundige kunstgewrochten, de raadsels nog hoogtij. Maar er wordt tevens veel gecijferd, met kleine en later ook met groote getallen.

Nu is de vraag die iedereen zich als vanzelf stelt: waarom volgen die scholen nog de oude richting? En 't antwoord is: zij kunnen moeilijk anders. Ziet, het bestaande heeft invloed en gevolgen. De H.B.S. en 't Gymn. vragen bij de toelating tot de eerste klas ook precies van die rekenkunstige aardigheden en nu moet de school, voorbereidende tot dat examen, wel in deze richting blijven voortgaan. Er bestaat een boekje: Repetitieboekje, I, Rekenen, van Boswijk, uitg. Wolters, Groningen, dat heet voor te bereiden tot die toelatings-examens, en dat veel te moeilijk is. (Ik heb dit tweemaal aangetoond uit de vraagstukken zelve). Maar de schrijver, thans Districts-Schoolopziener, was vroeger hoofd eener school voor M.U.L.O. Als nu zulk een persoon zoo'n boekje samenstelt, dan brengt hij èn H.B.S. èn Gymn. op een dwaalspoor. Zoo iemand, zeggen of oordeelen de leeraren dezer inrichtingen, weet het. En als ze dan vraagstukjes opgeven, die zelfs nog gemakkelijker zijn dan in dit Repetitieboek I, meenen ze derhalve volkomen in hun recht te zijn en niet te veel te eischen.

Wat de scholen voor M.U.L.O. betreft, de negenjarige voor leerlingen van 6-15 (of 16) jaar en de drie-, vier- of vijfjarige voor 12, 11, 10-15 à 16-jarigen, is het te hopen

[p. 693]

en m.i. stellig te verwachten, dat ze minder werk zullen maken van het oplossen van rekenkundige vraagstukken, omdat op deze inrichtingen ook, bijna zonder uitzondering, wiskunde wordt onderwezen. Evenwel wordt nog altijd, naar ik meen, op het eindexamen van die scholen voor 't Diploma A en B de oplossing van een vijftal rekenkundige voorstellen gevraagd. Ik heb ze eenige jaren lang, tot het jaar 1912, gezien, maar kon ze toen niet moeilijk vinden. En er waren groote cijferoefeningen bij.

Het doet mij groot genoegen, dat mevrouw S. Hoogendijk-Hesse haar afkeuring van de rekenkundige raadsels op de scholen voor M.U.L.O. in de Lelie heeft uitgedrukt. Wanneer ik b.v. vind dat de vraagstukken voor 't Diploma A en B (scholen M.U.L.O.) niet moeilijk waren, dan zegt dat niet veel. Ik kan daarover niet juist oordeelen. Wij onderwijzers over 't geheel vinden zulke vraagstukjes eenvoudig en 't kost ons moeite ons voor te stellen hoe een ontwikkeld mensch buiten het onderwijs er tegenover staat. Men groeit in een zekere richting en wordt zoo iets aparts. In vele gevallen oordeelt een buitenstaander beter, juister, meer onbevangen dan een vakman.

Bespreekt men een kwestie als deze in een vakblad, dan is de uitwerking gering. Men geeft je gelijk (ook wel niet), maar de zaak blijft als zij was. Daarom heeft V.E.O. (Vereeniging voor Vereenvoudiging van Onderwijs en Examens) zich indertijd gevormd buiten de vakmenschen, die er echter wel lid van kunnen zijn. Zij heeft veel geprobeerd en weinig, maar toch iets goeds, gedaan gekregen. Immers zoo menigmaal is 't voor ieder duidelijk dat er iets en wat er faalt, en toch - herstel blijft uit: Langzaam is Nederlandsch.

Daarom moet ons refrein zijn: frappez, frappez toujours! Welnu, ik zal voortgaan met kloppen. Reeds begint het te dagen in de Volksschool. Laat ons de luiken openzetten in de inrichtingen voorbereidende tot H.B.S. en Gymn. en in de scholen voor M.U.L.O.

C. GROUSTRA.