Logo DBNL
De Gids. Jaargang 154 (1991)

De Gids. Jaargang 154

(1991)– [tijdschrift] Gids, De–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

D. Frenkel
Computerspelletjes: de postmoderne wetenschap*

We zijn gewend aan het idee dat het enige decennia kan duren voordat een fundamentele wetenschappelijke ontdekking, bijvoorbeeld de transistor, resulteert in een produkt dat ons leven verrijkt, zoals een sleutelhanger die gaat piepen als je hem fluit. Maar de indruk bestaat dat binnen de wetenschappelijke wereld een nieuwe techniek binnen enkele weken, hooguit maanden gemeengoed is. Dat is niet altijd waar. Computersimulatie is een oude techniek, meer dan vijfendertig jaar oud. Dat is echt bejaard voor een wetenschappelijke discipline. Toch doet het vak simulatiekunde pas in de laatste jaren zijn intrede in het Nederlandse universitaire onderwijs. Vanwaar deze vertraging? Om dat te kunnen verklaren zal ik iets vertellen over de ontstaansgeschiedenis van dit vak. Ik zal een indruk geven van wat computersimulaties eigenlijk zijn en welke rol ze kunnen spelen in de fysica en chemie. Maar een beschrijving van de computerfysica heeft geen zin als ik niet eerst iets vertel over de natuurkunde eromheen.

‘Bang’ of ‘Whimper’

Ik heb soms de indruk dat de moderne natuurkunde door haar eigen succes in een soort midlife crisis terecht is gekomen. Een van de belangrijkste activiteiten in de natuurkunde van de twintigste eeuw was de speurtocht naar wat ik voor het gemak maar even de ‘Grondwet’ van de natuurkunde noem: de wet waaraan alle andere wetten moeten voldoen. Die speurtocht is tot nu toe een spectaculair succes geweest. Natuurwetten die niets met elkaar te maken lijken te hebben onder de gematigde condities die op aarde heersen, blijken onder extreme omstandigheden slechts een manifestatie te zijn van een diepere wet. Dit soort extreme omstandigheden kunnen worden gecreëerd in grote deeltjesversnellers. En nog veel extremere condities heersten tijdens de ‘Big Bang’, de eerste ogenblikken van het ontstaan van ons universum. De Grondwet van de natuurkunde mag dan ook worden beschouwd als de wet van de Big Bang.

Nu bestaat er bij twee groepen natuurkundigen het idee dat de speurtocht naar de Grondwet zijn einde nadert. De ene groep meent dat de Grondwet binnenkort gevonden zal zijn: de apotheose van de theoretische natuurkunde. Laat ik deze groep de ‘Big Bang’ school noemen. De tweede groep ziet geen licht aan het einde van de tunnel, maar merkt op dat deze tunnel, waarvan ieder nieuw segment veel duurder is dan het vorige, zich steeds verder van de aardse fysica verwijdert. Volgens deze groep, die ik voor het gemak maar de ‘Big Whimper’ school noem, zal de speurtocht doodlopen, omdat het zoeken naar de vermeende Grondwet nooit beëindigd zal zijn. De ‘Big Whimper’ school gaat ervan uit dat dit project dat was gestart als een poging tot generalisatie zal eindigen in een steriel superspecialisme of misschien wel een nieuwe vorm van theologie.

Hoe het ook zij, een grote groep natuurkundigen is van mening dat het grootste project

uit de natuurkunde zijn voltooiing, dan wel einde, nadert. Niet vandaag of morgen, maar in de komende decennia. En dat veroorzaakt onrust. Waarom? Om dat te kunnen uitleggen ga ik er maar even vanuit dat de Big Bang school gelijk krijgt. We investeren één jaar defensiebudget van de hele wereld in versnellers, telescopen en satellieten en geven alle theoretische hoge-energie fysici ontheffing van aardse beslommeringen zoals het schrijven van proposals en ingezonden brieven. En na een paar jaar is het zo ver: de Grondwet van de natuurkunde is af! En dan? Dan zijn er twee vragen: 1. Wat doen we ermee? en 2. Wat doen we erna?

De eerste vraag is niet zo onzinnig als ze op het eerste gezicht lijkt. De Grondwet van de natuurkunde heeft namelijk vrijwel zeker twee teleurstellende eigenschappen. De eerste is dat we de Grondwet voor de aardse fysica niet echt nodig hebben. Voor het dagelijks gebruik, dat wil zeggen onder condities die niet op die van de oerknal lijken, zijn de oudere wetten volstrekt adequaat. Sterker nog, de oude wetten zijn dan veel beter, want ze kunnen worden gebruikt om iets te verklaren, zoals: Waarom is de lucht blauw? Het is volstrekt zinloos om te trachten een dergelijke vraag direct vanuit de Grondwet te beantwoorden. Ik denk dan ook niet dat we in de komende decennia gesprekken zullen horen als: ‘Vader, waarom zijn kikkers groen?’ en dat de vader dan zegt: ‘Ja Jantje, om dat goed te kunnen uitleggen moet ik je toch eerst vertellen wat het Higgs boson is.’

Maar het is vaak onderstreept dat de speurtocht naar de Grondwet van de natuurkunde ook een breder cultureel belang heeft. En dat is zeker waar. Toch schuilt ook daar een probleem. Want hoewel er een groot verschil bestaat tussen wetten zoals die in de wetboeken staan en natuurwetten is er één belangrijke overeenkomst: beide zijn voor leken volstrekt onbegrijpelijk. Bij natuurwetten is dat tot op zekere hoogte onvermijdelijk. Galilei heeft al opgemerkt dat het boek van de natuur geschreven is in de taal der wiskunde, hoewel hij daarbij voornamelijk dacht aan meetkunde. Sinds Galilei's tijd is de wiskunde die nodig is om de fundamentele natuurwetten op te schrijven veel en veel complexer geworden. Het resultaat is dat we nu op weg zijn naar een Grondwet die weliswaar compact is, in het ideale geval één zin, maar niet simpel. Er is jarenlange studie vereist om de ‘eenvoud’ van de natuurwetten te kunnen zien.

Wat is nu het gevolg van het feit dat de fundamentele wetten van de natuurkunde voor negenennegentig procent van de bevolking onbegrijpelijk zijn? Het betekent iets heel onplezierigs, namelijk dat de meeste lezers van wetenschapsbijlagen en andere bronnen van populair-wetenschappelijke informatie de fundamentele natuurwetten accepteren op gezag van een ander, op gezag van de priesterkaste der natuurkundigen. Natuurlijk kan men het de fysici niet kwalijk nemen dat hun meest sexy theorieën alleen maar in parabelen aan het volk verteld kunnen worden. Maar gezond is het niet, want het gaat om geloof in het gezag van de spreker of schrijver. Ad Lagendijk heeft al betoogd dat dit niet goed is voor de geestelijke gezondheid van de fysici.1. Maar het is ook niet goed voor de rest van de bevolking, want wie één uitspraak moet accepteren op gezag van een ander, accepteert potentieel alles. Op dit punt loop ik even vooruit op de rest van mijn verhaal. Ik ben namelijk van mening dat de computer onze afhankelijkheid van een priesterkaste zal verminderen. Ik kan niet nalaten te citeren uit een recent essay in het blad Computers in Physics, waarin hoofdredacteur Bacon het volgende zegt: ‘Er verandert iets in de sociale structuur van de wetenschap; in het bijzonder wie er kunnen meedoen en welke vaardigheden vereist zijn. Bij die verandering zou het wel eens niet zozeer om een revolutie kunnen gaan als wel om een Wetenschappelijke Reformatie. De taal van de natuurkunde zou begrijpelijk kunnen worden voor het grote publiek.’2.

Ik hoop dit effect alsnog te illustreren. Maar eerst terug naar de vraag: ‘Wat doen we met de Grondwet van de Natuurkunde als die er

is?’ Het antwoord luidt, denk ik: ‘De meeste mensen doen er niets mee. En een kleine groep fysici zal hem intensief gebruiken.’ Op zichzelf is dat niets nieuws. In de geschiedenis van de natuurwetenschappen was er altijd maar een kleine groep mensen die echt gebruik maakte van de op dat moment bekende basiswetten. Maar de vraag is of het gebruik van de ‘theorie van het alles’ ooit vergelijkbaar zal worden met dat van de wetten van Newton of Maxwell. Ik denk van niet, omdat we, in tegenstelling tot bijvoorbeeld honderd jaar geleden, voor vrijwel de gehele natuurwetenschap van electronen, via kikkers tot kunstmanen, goed uit de voeten kunnen met de thans bekende basiswetten. Dat wil niet zeggen dat de natuurkunde ‘af’ is. Ik kom daar nog op terug.

De tweede vraag die ik stelde naar aanleiding van de mid-life crisis van de natuurkunde is: ‘Stel dat de definitieve “theorie van het alles” er komt, wat valt er dan nog te doen?’

In de meest extreme visie van de Big Bang school is er dan geen intellectuele uitdaging meer over in de natuurwetenschappen. De fundamentele vraag is opgelost en de rest is stom invulwerk. Vermoeiend, maar niet verhelderend: de fysica van de transpiratie na die van de inspiratie. Ik denk dat deze kijk berust op een misvatting. Namelijk dat kennis van alle natuurwetten begrip van alle natuurverschijnselen impliceert. Als we dezelfde criteria op de wiskunde zouden toepassen, dan zouden we moeten concluderen dat de vlakke meetkunde ‘af’ was op het moment dat Euclides zijn axiomata formuleerde.

Maar de werkelijkheid is anders. En misschien ligt hier wel de kern van de mid-life crisis van de natuurkunde: het aantal werkelijk exacte voorspellingen dat gedaan kan worden op grond van de fundamentele natuurwetten is vrijwel nihil. We hebben daarom werkelijk geen flauw benul van de mogelijke rijkdom aan verschijnselen die in deze wetten verborgen zit.

Om dit te illustreren gebruik ik een voorbeeld uit die andere ‘triviale’ wetenschap, de wiskunde. Vrijwel iedereen heeft wel eens plaatjes gezien van fractalen. Een bijzonder spectaculair voorbeeld is de zogeheten Mandelbrot-verzameling. Grafisch weergegeven laat deze verzameling oneindig complexe patronen zien die bij iedere verdere uitvergroting steeds weer een verrassende structuur vertonen. De ‘formule’ voor de Mandelbrot-verzameling is verbijsterend eenvoudig. Toch is de studie van fractalen iets van de laatste vijftien jaar. Ze waren er vroeger wel, maar we herkenden ze niet. Dankzij het werk van de wiskundige Benoit Mandelbrot zien we nu overal fractalen, ook in de natuur. Wolken, bergen, bliksems en ijsbloemen worden nu als fractalen herkend. En nu pas worden er wetten afgeleid die de fysica van fractale objecten beschrijven. Natuurlijk zijn die wetten gebaseerd op de bekende basiswetten van de fysica. Wat ik hiermee wil zeggen is dat in de natuurwetenschappen de basiswetten weliswaar belangrijk zijn, maar dat het minstens zo belangrijk is om een taal te hebben die ons in staat stelt om verschijnselen in de natuur te benoemen. Mandelbrot heeft één woord aan die taal toegevoegd. Daarmee heeft hij niet een nieuwe natuurwet ontdekt, maar wel de voorwaarde geschapen waaronder zulke nieuwe wetten kunnen worden geformuleerd. Dat lijkt mij een fundamentele stap. En ik heb geen reden om aan te nemen dat er niet veel meer verschijnselen zijn die wij dagelijks zien, maar nog niet als systematisch herkennen. In die zin is de grote mislukking van de moderne natuurkunde de basis voor het voortbestaan van deze tak van onderzoek: ‘There's no success like failure’... de natuurkunde wordt nooit volwassen.

Hoewel de fundamentele natuurwetten niet erg geschikt zijn om verschijnselen te voorspellen, zijn ze wel geschikt om andere, ‘hogere’ natuurwetten af te leiden: zo moeten uit de Grondwet van de natuurkunde de wetten van de gewone quantummechanica volgen. En uit de wetten van de quantummechanica volgen weer de wetten van de Newton die beschrijven hoe macroscopische objecten bewegen. Maar zelfs uit de wetten van Newton volgen geen

exacte voorspellingen als het aantal bewegende objecten groter is dan twee. Toch volgen uit de wetten van Newton, na enig gesleutel, de wetten van de hydrodynamica die beschrijven hoe water en lucht, samengesteld uit duizenden triljarden moleculen, bewegen. Maar alweer, de wetten van de hydrodynamica leiden alleen in uitzonderlijke omstandigheden tot exacte voorspellingen. Er is dus een hiërarchie van wetten in de natuurkunde. Het lijkt wel of de hele natuurkunde een flatgebouw is dat is opgebouwd uit redelijk gescheiden verdiepingen. Iedere verdieping rust op de onderliggende, maar afgezien daarvan merk je meestal niet veel van de benedenburen. Iedere verdieping heeft haar eigen vloer: de lokaal geldende natuurwet. Als we een klusje willen doen op de zeventiende verdieping, bijvoorbeeld een lamp verwisselen, dan blijven we niet op de begane grond staan. We begeven ons eerst naar de zeventiende verdieping, gaan op onze tenen staan en proberen de lamp te verwisselen. Helaas lukt zelfs dat meestal niet. In zekere zin is dit de grote teleurstelling en tegelijk de grote uitdaging van de moderne natuurkunde: we hebben een heel flatgebouw van natuurwetten, maar we kunnen het lampje op de zeventiende verdieping niet verwisselen. We hebben een keukentrapje nodig. Dat keukentrapje is de computer. Eigenlijk is de situatie nog erger: zelfs met het keukentrapje kunnen we nog vrijwel nergens bij. Maar ik wil mij hier beperken tot wat wij wel kunnen.

Het keukentrapje

De invoering van de computer wordt wel eens de tweede industriële revolutie genoemd. Ik weet dat dit een cliché is, maar ik schaam mij er niet voor om dit cliché hier te herhalen. Hoe kunnen wij, de tijdgenoten, weten dat hier sprake is van een omwenteling? Ik denk dat we die conclusie alleen maar op indirecte argumenten kunnen baseren. David Bolter heeft, in zijn boek Turing's Man, een dergelijk indirect argument genoemd.3. Bolter zegt dat ieder tijdperk zijn ‘defining technology’ heeft. Daarmee bedoelt hij de technologie die steeds opduikt in de metaforen waarin wij onszelf en de wereld om ons heen beschrijven. Bij de Grieken was de ‘defining technology’ ontleend an het pottenbakken en spinnen: denk maar aan de Schikgodinnen die onze levensdraad spinnen. Vanaf de late middeleeuwen was het de klok en, vooral in Nederland, de windmolen die in vele metaforen opdook. In de negentiende eeuw was het de stoommachine. Onze taal zit nog vol met uitdrukkingen die daarnaar verwijzen. En nu is de computer de ‘defining technology’. In toenemende mate spreken mensen in de industriële wereld over zichzelf in computer-termen: de hersenen worden vergeleken met een grote rekenmachine, communicatie met de buitenwereld met input-output-operaties. Het beeld dat we van onszelf hebben, wordt bepaald door de computer; niet door de televisie of het vliegtuig.

Laten we er dus maar even van uitgaan dat we te maken hebben met een revolutie. Dan is een voor de hand liggende reactie: wat een verpletterend saaie revolutie! Computers worden in overgrote meerderheid gebruikt als schrijfmachine, als archiefkast of als naslagwerk: het lijkt wel de revolutie van de Dorknopers.

Maar in de natuurwetenschappen ligt de situatie anders. De manier waarop we onderzoek doen is door de computer veranderd. In de β-vakken gebruiken we de computer om bepaalde aspecten van de wereld na te bootsen, als in een computerspelletje. In zekere zin spelen we voor God: we kunnen in de computer iedere model-wereld scheppen die we willen. In de praktijk betekent dit dat we een model bedenken voor het systeem dat we willen bestuderen: bijvoorbeeld een stromende vloeistof, of de atmosfeer van de aarde of zelfs het hele universum. Daarna vertellen wij aan de computer hoe de natuurwetten er uitzien. Niet de Grondwet, maar de wet die van toepassing is op de verschijnselen die we willen bekijken. En dan zeggen we tegen de computer: ‘Dit zijn de spelregels, reken nu maar uit wat er gaat gebeuren.’ En daarna kijken we

gewoon wat er gebeurt met onze schepping. We doen een Computer Experiment.

Hiermee is in grote lijnen geschetst hoe we een computer-simulatie doen, maar nog steeds niet waarom. Om goed te kunnen vertellen welke rol computer-simulaties spelen in de β-wetenschappen moet ik even terugkomen op iets dat ik al een paar keer noemde: de ons bekende natuurwetten leiden vrijwel nooit tot exacte voorspellingen. Stel dat we de wetten van de klassieke mechanica van Newton willen gebruiken om de beweging uit te rekenen van drie of meer deeltjes die krachten op elkaar uitoefenen. Dan kan dat niet exact, dat wil zeggen, niet met potlood en papier. Het kan ook niet exact met de computer. Maar met een computer kunnen we in veel gevallen wel het exacte antwoord tot iedere gewenste nauwkeurigheid benaderen. Met potlood en papier is dat niet principieel onmogelijk, maar wel ondoenlijk.

Nu is het zo dat vrijwel alle materialen die wij bestuderen in de chemie en de fysica zijn opgebouwd uit heel veel atomen of moleculen. Met ‘heel veel’ bedoel ik alleen maar: meer dan twee. Stel nu dat we de fysische eigenschappen van een vloeistof willen uitrekenen, dan is het volstrekt onmogelijk om het exacte antwoord te vinden met behulp van analytische technieken (zeg maar: potlood en papier). Nu moet ik hierbij opmerken dat vloeistoffen wel een bijzonder moeilijk geval zijn. Zo moeilijk dat ook voor de komst van de computer al duidelijk was dat je er met polood en papier alléén niet uitkwam. Daarom werd al sedert de jaren twintig gezocht naar alternatieve technieken om iets te weten te komen over de microscopische structuur van vloeistoffen. De meest succesvolle aanpak in de pre-computer tijd was het bouwen van schaal-modellen van vloeistoffen. Om een handzaam model te krijgen moeten we de schaal met een factor tienmiljoen vergroten. Dan kunnen we atomen vervangen door rubber balletjes of kogellagerkogeltjes. Maar hoe maken we met die bolletjes een model voor een vloeistof? Bij mijn weten is de eerste die zich met dit probleem heeft beziggehouden de Groningse fysicus Prins.4. In zijn openbare les van 1928 beschrijft hij hoe hij een twee-dimensionaal model voor een vloeistof maakte door plantezaadjes, dan wel een schot hagel, op een glasplaat uit te strooien. Maar het meest uitvoerige onderzoek aan mechanische modellen voor vloeistoffen is uitgevoerd door de Engelsman J.D. Bernal, onderzoeker en vriend van de verdrukten en zwakken dezer aarde, in het bijzonder van het zwakke geslacht.5. Eerlijkheidshalve moet ik hieraan toevoegen dat het meest tijdrovende werk, namelijk het analyseren van de gebouwde drie-dimensionale structuren, werd uitgevoerd door Bernals talrijke assistentes, zoals bijvoorbeeld de beklagenswaardige juffrouw Wilkinson die moest nagaan op hoeveel verschillende manieren samengeperste balletjes van schuimplastic lokaal geordend kunnen zijn: zij vond dat er tenminste honderdzevenennegentig verschillende configuraties mogelijk waren. Het is verhelderend om te lezen hoe Bernal zijn mechanische modellen construeerde. In het volgende citaat beschrijft Bernal hoe hij met behulp van stokjes en rubber balletjes een model voor een vloeistof bouwde: ‘(...) Ik nam een aantal rubber balletjes en verbond die met stokjes die in lengte varieerden tussen de 2,75 en 4 inch. Ik probeerde dit zo slordig mogelijk te doen door op mijn eigen kamer te werken. Ik werd daar namelijk iedere vijf minuten of zo gestoord zodat ik mij niet herinnerde waar ik voor de onderbreking was gebleven. Maar (...)’ en dan bespreekt Bernal enkele nadelen van het aldus gebouwde model. Een betere methode was om duizenden stalen kogeltjes in een rubber ballon te stoppen en te kijken hoe die zich rangschikken. Een groot bezwaar van mechanische modellen is echter dat het, zonder de hulp van Bernals assistentes, heel moeilijk is om naast mooie plaatjes ook echt kwantitatieve informatie te verkrijgen. En dat brengt me dan uiteindelijk bij de computer.

De eerste computer-simulaties dateren uit het begin van de jaren vijftig, en ze vonden plaats daar waar de eerste elektronische com-

puters stonden, namelijk in de Amerikaanse regeringslaboratoria. De eerste computers die vrijkwamen voor niet-militaire research werden ingezet op onderzoeksgebieden waar groot gebrek bestond aan exacte theoretische resultaten. De studie van vloeistoffen was daar één van, juist omdat dit een gebied was waar men met potlood en papier alléén veel minder kon beginnen dan bijvoorbeeld bij de studie van gassen of vaste stoffen. De eerste numerieke simulatie van een vloeistof werd in 1953 uitgevoerd door Metropolis, Rosenbluth, Rosenbluth, Teller en Teller op de maniac computer in Los Alamos.6. Zij gebruikten bij deze berekeningen een numerieke techniek die bekend staat als de Monte Carlo-methode. Metropolis en Ulam bedachten de naam ‘Monte Carlo-simulatie’, een verwijzing naar het feit dat bij dit soort berekeningen intensief gebruik wordt gemaakt van willekeurig verdeelde getallen. Een alledaagse manier om dit soort getallen te genereren is het gooien van een dobbelsteen of het draaien van een roulettewiel. Dit laatste verklaart de naam van de Monte Carlo-techniek. Ik zal hier niets zeggen over de technische aspecten van computer-simulaties, op één opmerking na, namelijk dat de Monte Carlo-methode van Metropolis niet alleen belangrijk is, maar ook eenvoudig. Zo eenvoudig dat het naar mijn mening thuishoort op het curriculum van de middelbare school.

Drie jaar later, in 1956, introduceerde Berni Alder, die verbonden was aan het Lawrence Livermore National Lab., een nieuwe simulatie-techniek, ook heel eenvoudig, die het mogelijk maakte om moleculaire bewegingen in vloeistoffen te simuleren.7. Deze techniek werd, tamelijk prozaïsch, de Moleculaire Dynamicamethode genoemd.

Aanvankelijk werden computer-simulaties met reserve ontvangen, omdat ze niet goed konden worden ingepast in de bestaande disciplines. Het was geen theorie maar ook geen experiment. En het produceerde getallen die niemand op een andere manier kon verifiëren. Maar het botweg negeren van computer-simulaties werd steeds moeilijker, zoals moge blijken uit het volgende autobiografische citaat van George Vineyard, een derde grondlegger van de computer fysica. Vineyard, werkzaam bij Brookhaven National Laboratory, gebruikte als eerste de computer om stralingsschade in metalen te bestuderen. Hij zegt hierover het volgende:

‘In de zomer van 1957 hield ik een voordracht over stralingsschade in metalen op de Gordon Conferentie over de Chemie en Fysica van Metalen (...). Na de voordracht was er een levendige discussie (...). Op een gegeven moment werd het idee naar voren gebracht dat je een computer zou kunnen gebruiken om in meer detail na te gaan wat er nu eigenlijk gebeurt tijdens stralingsschade cascades. Het werd een heel debat, waarin sommigen betoogden dat het niet mogelijk was om dit met een computer te doen, en anderen dat het niet nodig was. John Fisher verkondigde met nadruk dat dit een karwei was dat zonder meer met potlood en papier kon worden geklaard, en hij liet zich verleiden tot de belofte om dit te demonstreren. Hij vertrok naar zijn kamer om te werken. De volgende ochtend vroeg hij om een beetje meer tijd. Hij beloofde mij de resultaten spoedig op te sturen als hij weer thuis was. Toen ik na twee weken nog steeds niets van hem had gehoord, belde ik hem op en hij gaf toe dat hij het had opgegeven. Dit was voor mij een stimulans toch maar wat meer na te denken over de mogelijkheden om een snelle computer in te zetten, in plaats van John Fisher...’8.

Gedurende de jaren vijftig waren computersimulaties nog op zoek naar hun plaats binnen de natuurwetenschappen. De jaren zestig lieten een langzame groei zien. Zelfs tegen 1970 waren er over de hele wereld verspreid minder dan twintig groepen actief op dit gebied. Maar aan het eind van de jaren zestig kregen de meeste universiteiten hun eigen computers. De jaren zeventig waren dan ook een periode van snelle groei: computer-simulaties werden in toenemende mate een standaardhulpmiddel bij het onderzoek. En nu hebben de meeste

universiteiten computer-simulatietechnieken in hun curriculum opgenomen.

De werkelijkheid achter de schermen?

Waarvoor gebruiken wij computer-simulaties? Ik noem drie essentieel verschillende toepassingen. De eerste toepassing is weinig opzienbarend. We gebruiken de computer om de eigenschappen van bestaande of nieuwe materialen te voorspellen. Eigenlijk is het helemaal niet zo vanzelfsprekend dat we daar een computer voor gebruiken. Stel dat we het smeltpunt van ijs willen weten, dan lijkt het nog altijd veel gemakkelijker om een thermometer in een smeltend ijsblokje te steken dan om een computer-simulatie te doen. Dat is natuurlijk ook zo, maar het is een stuk moeilijker en daarom ook duurder om de fysische eigenschappen te meten van materialen bij extreem hoge drukken of temperaturen. Voor de computer maakt die laatste omstandigheid niets uit. Als ik een simulatie doe van een materiaal bij vijfduizend graden Celsius, gaat mijn beeldscherm niet in rook op. We kunnen computer-simulaties ook gebruiken als hulpmiddel bij de voorbereiding en analyse van arbeidsintensieve experimenten. Het scala van toepassingen van computer-simulatie als verlengstuk van het experiment wordt de laatste paar jaar snel breder.

De tweede belangrijke toepassing van computer-simulaties is het toetsen van theorieën. Dat lijkt een vreemde toepassing. We hebben allemaal geleerd dat er maar één test is voor een theorie, namelijk de vergelijking met het experiment. En dat is ook zo. Maar als we bijvoorbeeld het vriespunt van een vloeistofmengsel willen berekenen, dan doet zich het probleem voor dat we met potlood en papier alléén geen exacte voorspellingen kunnen doen. Dat lijkt op het eerste gezicht misschien niet erg, want als we er met potlood en papier niet uitkomen, dan hebben we nog altijd de computer. Toch is dat niet goed vergelijkbaar. Computerberekeningen geven weliswaar een antwoord, maar dat antwoord is een getal, en van één enkel getal leren we niets. We zijn geïnteresseerd in verbanden of beter nog, in begrijpelijke verklaringen. Theorieën geven ons zulke verklaringen, simulaties niet. Daarom is het uiteindelijk altijd beter om een simpele theorie te hebben dan een computerprogramma. Maar om een theorie te maken die we wel met potlood en papier aan kunnen, moeten we allerlei drastische vereenvoudigingen doorvoeren. Ik neem als voorbeeld weer de theorie die voorspelt hoe het vriespunt van een vloeistofmengsel afhangt van de krachten die vloeistofmoleculen op elkaar uitoefenen. Een dergelijke theorie bestaat sinds een paar jaar: daarin zitten benaderingen van onbekende kwaliteit. Maar er is een probleem: ook de krachten tussen de moleculen kennen wij niet goed. Dus niet alleen zitten in de theorie die we gebruiken benaderingen, maar ook de gegevens die wij nodig hebben voor onze theoretische voorspelling zijn niet exact. Toch gaan we vergelijken met het experiment. En dan blijkt dat het gemeten smeltpunt in het geheel niet klopt met de theoretische voorspelling. Wat betekent dat dan? Dat de theorie niet deugt? Mogelijk. Of misschien is de theorie wel goed, maar is onze schatting van de krachten tussen de moleculen heel slecht? Dat vertelt het experiment ons niet. In dit soort situaties is vergelijking met een echt experiment dus geen goede test van een theorie.

Maar nu bestaat er de mogelijkheid om de theorie met een computer-simulatie te vergelijken. Voor computerberekeningen moeten wij ook eerst een model kiezen, dat wil zeggen: de krachten tussen de moleculen specificeren. En daarna berekenen wij de ligging van het smeltpunt. Zo nauwkeurig als we maar willen. En die ‘exacte’ berekening vergelijken we dan met de theoretische voorspelling. Als theorie en computerexperiment nu niet overeenstemmen, is er echt iets mis met de benaderingen in de theorie, want de theorie en de simulatie veronderstellen allebei dezelfde krachten tussen de moleculen.

Een dergelijke berekening waarbij de computer-simulatie de rol van het experiment

overneemt noemen wij een ‘computerexperiment’. We gebruiken computerexperimenten om theorieën te testen voordat we ze op de echte wereld loslaten. Dit is een van de belangrijkste toepassingen geworden van computersimulaties. In de afgelopen decennia zijn een aantal eerbiedwaardige theorieën door computerexperimenten onderuit gehaald. Ook de recente theorie voor het vriespunt van vloeistofmengsels, die ik in het voorbeeld noemde, heeft de confrontatie met het computerexperiment niet zonder kleerscheuren doorstaan.9. Computer-simulaties zijn om die reden een belangrijk onderdeel van theoretisch onderzoek geworden: niet als vervanging van theorie, maar als hulpmiddel bij de constructie van nieuwe theorieën: een soort kwaliteitscontrole in de fabriek.

Laat mij nog één toepassing van computersimulaties noemen, namelijk de ‘ontdekkingsreis per computer’. Deze toepassing was voor de komst van de computer eigenlijk nooit overwogen. Toch is het misschien wel de belangrijkste. Zoals Alice door de spiegel in haar eigen droomwereld stapt, zo stappen wij door het beeldscherm en gaan op onderzoek uit in onze gesimuleerde wereld. In die wereld gelden simpele spelregels: de natuurwetten die wij zelf aan de computer hebben opgegeven. Toch ontdekken we vaak onverwachte verschijnselen. Ik zal dit illustreren aan de hand van een voorbeeld dat mijzelf na aan het hart ligt: de structuur van vloeibare kristallen. Daartoe moet ik eerst vertellen wat vloeibare kristallen zijn. We kennen ze allemaal: ze zitten bijvoorbeeld in het scherm van een zakrekenmachine of van een digitaal horloge. Maar hoe zien vloeibare kristallen er op moleculaire schaal uit? De essentie kan in twee minuten worden verteld. Op school hebben we geleerd dat de materie in drie fasen kan voorkomen: gas, vloeistof en vaste stof. In een typische kristallijne vaste stof liggen de moleculen geordend in een regelmatig drie-dimensionaal rooster, als flessen in een wijnrek. Als we een kristal verwarmen, smelt het. In de resulterende vloeistof-fase zijn de moleculen niet langer geordend in een rooster. Een mooi model voor een moleculaire vloeistof is een pan met rijst: de rijstkorrels liggen wanordelijk door elkaar en hebben geen voorkeursrichting. Zoiets heet een ‘isotrope vloeistof’. Maar het is nu al 101 jaar bekend dat er kristallen zijn die bij het smeltpunt niet overgaan in een isotrope vloeistof: zelfs boven het smeltpunt blijft een gedeelte van de kristallijne orde bestaan. Dit soort gedeeltelijk geordende vloeistoffen heet vloeibare kristallen. Er zijn veel verschillende vloeibare kristallen: de naam hangt af van de mate van ordening. In het eenvoudigste vloeibare kristal liggen de moleculen gemiddeld parallel, maar verder wanordelijk. Deze fase heeft de weinig verhelderende naam ‘nematisch’. Mijn bureau is een goed model voor een nematisch vloeibaar kristal: de papieren liggen allemaal parallel aan het tafeloppervlak, maar verder strikt wanordelijk. Een stapje verder naar het kristal toe vinden we een vloeibaar kristal met de evenmin verhelderende naam Smectisch-A. Deze fase lijkt op de nematische fase, maar nu zijn de moleculen ook nog in laagjes geordend. Binnen deze laagjes heerst geen kristallijne orde. Deze smectische fase heeft dus kristalachtige orde in één richting en vloeistof-wanorde in de overgebleven twee richtingen, als een mensenmenigte in een warenhuis. Nog dichter bij het kristal staat de columnaire fase. Eindelijk een naam die iets betekent: de moleculen zijn wanordelijk gestapeld in parallelle kolommen, maar die kolommen vormen een regelmatig tweedimensionaal rooster, dus: kristallijne orde in twee richtingen en vloeistof-wanorde in de derde. Uit dit uiterst summiere overzicht blijkt één ding: vloeibare kristallen vormen de brug tussen gewone vloeistoffen en geordende kristallen. Maar er is iets vreemds: alle moleculaire stoffen vormen bij lage temperaturen een kristal, maar slechts een fractie heeft ook een vloeibaar kristallijne fase. De grote vraag is: waarom sommige wel en andere niet? Die vraag is niet eenvoudig te beantwoorden, omdat vloeibare kristallen uit grote organische moleculen of zelfs macromoleculen bestaan. Die moleculen

zijn buigzaam, ze stoten elkaar af op korte afstanden en ze trekken elkaar aan op lange afstanden en die krachten zijn hoekafhankelijk, dat wil zeggen: ze veranderen sterk als we de moleculen ten opzichte van elkaar draaien. Wat is nu echt nodig om een stabiel vloeibaar kristal te krijgen? Aantrekking, afstoting of flexibiliteit? In de theoretische literatuur van de afgelopen veertig jaar treffen we argumenten aan voor alle drie, maar hoekafhankelijke aantrekking leek toch lange tijd favoriet. Nu bestond er in de begintijd van de computer een analoge situatie met betrekking tot de vraag waarom vloeistoffen bevriezen. Men vroeg zich af welke intermoleculaire krachten nu echt nodig zijn om moleculen spontaan in een kristal te doen ordenen. ‘Afstoting is genoeg,’ zei de fysico-chemicus Kirkwood. ‘Zonder aantrekking lukt het niet,’ zeiden velen van zijn vakgenoten. Een beroemd geworden computer-simulatie van Alder en Wood liet zien dat een systeem van puur repulsieve harde bollen een goed gedefinieerd vriespunt heeft.10. Dat resultaat is inmiddels algemeen aanvaard, maar dertig jaar geleden stuitte het op ongeloof. Dat kan ik illustreren aan de hand van het verslag van een discussie over dit onderwerp uit 1957. Vijftien eminente onderzoekers, onder wie twee Nobelprijswinnaars, bespraken de gloednieuwe computer-simulaties.11. Op voorstel van onze landgenoot Uhlenbeck werd er, na een lange discussie, gestemd over de vraag of harde bollen nu wel of niet konden

illustratie

kristalliseren. De helft van de aanwezigen, inclusief Uhlenbeck, stemde toen tegen. Maar tegenwoordig wordt, dankzij de computer-simulaties van Alder, de kristallisatie van harde bollen beschouwd als het prototype van de vloeistof-vast overgang in atomaire systemen. Nu kunnen we ons afvragen of de vorming van vloeibare kristallen ook terug te voeren is tot het effect van de harde afstoting tussen de moleculen. Als we de leerboeken over vloeibare kristallen bekijken, dan lijkt het antwoord duidelijk: de Noor Onsager heeft in de jaren veertig aangetoond dat dunne harde staafjes bij verhoging van de dichtheid een nematisch vloeibaar kristal moeten vormen.12. In gewone woorden: je kunt meer ongekookte spaghetti in een bus doen door de staafjes parallel te houden dan door ze, als mikado-stokjes, kriskras door elkaar te laten liggen. Maar geen van de huidige leerboeken beschouwt de mogelijkheid dat harde, niet-bolvormige deeltjes spontaan een gelaagde, smectische, fase dan wel een kolomfase kunnen vormen. Om hierover meer te weten te komen hebben wij computersimulaties gedaan: simulaties als exploratie. Eerst vonden wij iets dat niet verbazend was: namelijk dat een vloeistof van langgerekte, ellipsoidale deeltjes bij lage dichtheden isotroop is, maar bij hogere dichtheden spontaan nematisch wordt. Dit wordt geïllustreerd door twee fotos die een simulatie te zien geven van een systeem van harde ellipsoiden waarvan de lengte vijf maal groter is dan de breedte. Bij

illustratie

lage dichtheid zijn de moleculen in de vloeistof ongericht, maar na compressie gaan de moleculen gemiddeld parallel staan. Deze oriëntatie-ordeningsovergang zien wij ook als we, in plaats van ellipsoidale deeltjes, staafjes met een bolvormige kap beschouwen. Weer zien wij bij lage dichtheid een isotrope fase en bij hogere dichtheid een nematisch vloeibaar kristal. Maar nu gebeurt er iets bijzonders. Als wij de fase met oriëntatie-ordening nog verder samendrukken, ordenen de moleculen zich spontaan in laagjes: de staafjes vormen een smectisch vloeibaar kristal! Bedenk wel dat dit gewone harde staafjes zijn, zeg maar: krijtjes. Ter vergelijking één echt experiment, namelijk een electronenmicroscoop-opname gemaakt door de Japanner Hachisu. Hachisu bestudeerde een suspensie van β-ferri-oxyhydroxide. Dit materiaal heeft de eigenschap om spontaan harde staafvormige colloidale deeltjes te vormen, zeg maar harde staafjes. Bij hoge concentraties blijken deze staafjes zich als een smectisch vloeibaar kristal te gedragen: de gelijkenis met de computer-simulatie is treffend. Als we harde plaatjes simuleren, in plaats van harde staafjes, vinden we nog een fase: de kolomfase. We menen zelfs een extra fase te hebben gevonden die experimenteel nog niet is waargenomen. Voor mij waren deze berekeningen een ontdekkingsreis per computer. Dit soort computerspelletjes geeft ons nieuw inzicht en stimuleert nieuw theoretisch en experimenteel werk.



illustratie

Zoals uit het voorgaande moge blijken, veranderen computers de manier waarop wij onderzoek doen, zowel experimenteel als theoretisch. Computerfysica wordt daarom wel eens aangeduid als de ‘derde tak van de natuurkunde’. Dat is een gevaarlijke term in een land als Nederland waar de verzuiling altijd op de loer ligt. Het ergste dat er met de computerfysica kan gebeuren, is dat deze zich zou afzonderen in eigen instituten en werkgemeenschappen. Ik zie computerfysica niet als een vak voor specialisten, maar als een manier van werken die iedere onderzoeker, experimenteel of theoretisch, in toenemende mate zelf zal weten toe te passen.

Bij banken en overheidsinstellingen wordt de computer vaak aan de argeloze cliënt voorgesteld als een soort wrede, wispelturige godheid die zich onttrekt aan iedere menselijke controle. Deze kijk op computers is het onvermijdelijke gevolg van een structuur waarin de gebruiker die vragen stelt aan de computer, niet betrokken is geweest bij het ‘in-programmeren’ van de antwoorden. Dit leidt maar al te gemakkelijk tot een situatie waarin de computer-gebruiker zijn of haar eigen verstand ondergeschikt maakt aan het vermeende ‘hogere weten’ van de computer. Dat is een ongewenste situatie die echter niet onomkeerbaar is, als we de scheiding weten te slechten tussen de ‘gebruiker’ die vragen stelt en de ‘deskundige’ die de computer leert te antwoorden. In de natuurwetenschappen kan die scheiding verdwijnen,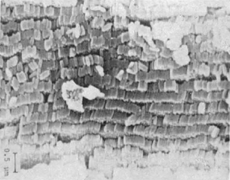

illustratie

als we ons maar kunnen losmaken van de idee-fixe dat iedere nieuwe deskundigheid baat zou hebben bij het stichten van een eigen wetenschappelijk koninkrijk.


Vorige Volgende

Over dit hoofdstuk/artikel

auteurs


datums