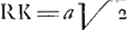Oeuvres complètes. Tome X. Correspondance 1691-1695

N^o 2829.
G.W. Leibniz à Christiaan Huygens.
11 octobre 1693.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et C.I. Gerhardt²⁾.
Elle est la réponse au No. 2822.
Chr. Huygens y répondit par sa lettre du 29 mai 1694.

Hannover, ce 1/11 d'Octobre 1693.

Monsieur

Je suis ravi d'apprendre de temps en temps des nouvelles de vostre santé, qui nous doit estre chere. Car le monde se peut encor promettre beaucoup de vos

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 163.

2) Leibnizens Mathematische Schriften, II, p. 163 et Brieswechsel, p. 719.

[p. 539]

decouvertes. Ainsi quand vos lettres ne contiendroient que cela, elles me seroient tousiours agreables, Mais il y a tousiours beaucoup à apprendre; et de plus vos obligeantes expressions, qui font connoistre avec combien de bonté vous voulés bien: meas esse aliquid putare nugas, m'engagent à vous en faire des remercimens.

Je seray ravi de voir un jour vos repliques sur nostre question physique, car comme vous approfondisséz merveilleusement ces choses, et comme il semble que nous avons pris un nouveau tour pour éclaircir la question des Atomes et du Vuide, j'espere que nous la pourrons enfin terminer. Je souhaiterois de voir ce que vous avés remarqué sur mes animadversions anti-cartesiennes, que vous n'aviés pas trouvées tout à fait mauvaises³⁾.

J'ay aussi receu quelques lettres de M. le Marquis de l'Hospital, ou j'ay repondu le mieux que j'ay pû⁴⁾. Mais mes distractions ne m'ont point permis de luy donner toute la satisfaction que j'aurois bien desiré pouvoir donner. Je n'ay pas manqué d'envoyer à Messieurs les Collecteurs des Actes de Leipzig ce que vous leur avés destiné sur le probleme de Mons. Bernouilli⁵⁾; il est vray que c'a esté une semaine apres l'arrivée de vostre lettre, que j'ay trouvée à mon retour d'un petit voyage fait pour suspendre mes travaux durant quelques iours, car ie me trouvois peu propre à l'application, apres une fieure tierce, qui n'a pas esté trop forte, mais qui m'a fait craindre une recheute. Comme j'avois toutes les commodités dans le voyage et avec cela l'esprit libre, je m'en suis bien trouvé.

Tout ce que je m'estois proposé en produisant le nouveau calcul, que vous commencés, Monsieur de trouver commode, a esté d'ouvrir un chemin ou des personnes plus penetrantes que moy pourroient trouver quelque chose d'importance. Et maintenant voti damnatus sum, depuis que vous trouvés bon de vous en servir et c'est me faire beaucoup d'honneur que de le declarer publiquement⁵⁾. Je suis ravi de voir par vostre solution du probleme de M. Bernoulli, que vous avés remarqué ce qu'il y a de plus beau dans nostre calcul differentiel, aussi tost que vous avés voulu prendre la peine d'y entrer, c'est iustement ce que ie marquois autres fois⁶⁾ d'y estimer, sçavoir qu'il nous donne des solutions generales qui menent naturellement aux Transcendentes, mais qui dans certains cas font que la Transcendalité se perd et qu'on decouvre que la ligne est ordinaire.

Vous faites beaucoup d'honneur à la Geometrie lorsque vous trouvés les plus beaux usages des lignes qu'elle peut fournir. Et cette nouvelle courbe, que vous ne donnés que par enigme⁵⁾, en sera une belle preuve aussi bien que vostre usage

3) Voir la Lettre N^o. 2759 à la page 302.

4) La correspondance de Leibnitz et de l'Hospital a été publiée par Gerhardt dans ‘Leibnizens Mathematische Schriften’, Band II, p. 216-343.

5) Voir la pièce N^o. 2823.

5) Voir la pièce N^o. 2823.

6) Comparez la Lettre N^o. 2639 à la page 558.

5) Voir la pièce N^o. 2823.

[p. 540]

de la cycloide l'a esté autres fois. La construction des lignes, que vous appellés Tractorias est d'importance. J'appelle ainsi plustost la construction que la ligne, car toute ligne peut estre construite de cette façon, prenant tousjours dans la Tangente un point dont la distance du point de la courbe soit donnée, ce qui fera une nouvelle ligne, le long de la quelle un bout du fil estant mené l'autre decrira la courbe donnée. Vous estes tombé de vous même sur une idée, que j'avois deja, mais que j'ay apprise d'un autre. C'est de feu Mr. Perraut le Medecin⁷⁾, qui me proposa de trouver quelle ligne se produit en menant une extremité du fil le long d'une regle, pendant que l'autre extremité tire un poids par le plan horizontal dans le quel la regle tombe. Je trouvay bien tost que c'est la quadratrice de la figure des tangentes canoniques du cercle, et par consequent dependante de la quadrature de l'Hyperbole⁸⁾. Je croyois d'avoir seul cette application de ce mouvement, mais dernierement j'ay iugé par ce que M. Bernoulli a dit sur le probleme de son frere⁹⁾ que vous deviés avoir publié la même chose dans l'Histoire des ouvrages des sçavans¹⁰⁾, car je n'ay pas encor eu cette Histoire des ouvrages de cette année par la negligence du libraire, à qui j'avois ecrit pour m'envoyer et cela et autres choses. Or cela m'a convié à publier encor d'autres pensées que j'avois sur l'usage de ce mouvement¹¹⁾. Et comme il paroist que vous avés medité sur les moyens de le rendre exact en pratique, vous trouverés qu'il y a peut estre pas un en Geometrie qui le merite d'avantage. On pourroit se servir soit d'un poids, soit d'une appression elastique, comme par exemple en mettant un ressort entre deux plans paralleles immobiles, qui le tiendroient pressé. Ce ressort couleroit entre ces deux plans, d'une manière à ne pouvoir changer de situation à leur egard^a), et presseroit un stile contre l'un des plans. Le style seroit attaché au ressort, et le fil qui tireroit l'un et l'autre, quoyqu'il n'iroit peut estre point jusqu'au stile deuuroit pourtant y aboutir en cas de prolongation ou plustost à l'axe prolongvé du stile à l'entour du quel le fil, ou bien la regle équivalente au fil, se tourneroit pendant le mouvement. Il seroit meme possible de faire que le ressort 571-580

7) Comparez, pour ce qui va suivre, la note 4 de la pièce N^o. 2824.

8) Consultez à ce propos la page 388 de l'article de Leibniz cité dans la note 6 de la pièce N^o. 2824. On y verra que ‘la figure des tangentes canoniques du cercle’ dont la tractrice peut être considérée comme quadratrice, n'est autre que la courbe αψθ de la figure 5 de la pièce N^o. 2625, dont les ordonnées sont égales aux tangentes des angles σδε. Ainsi, pour connaître l'aire de cette courbe, il ne s'agit que de trouver ce que Leibniz appelle dans sa Lettre N^o. 2699 à la page 161: ‘la somme des tangentes selon les sinus de complement’ qu'il réduit à la page suivante de la même Lettre à la quadrature de l'hyperbole.

9) Voir la note 19 de la Lettre N^o. 2819.

10) Voir la pièce N^o. 2793.

11) Toujours dans l'article cité dans la note 6 de la pièce N^o. 2824.

a) Cela serait difficile [Christiaan Huygens].

[p. 541]

(un ou plusieurs) estant pressé entre les deux plans, le stile qui doit tracer, fut dehors, pour qu'on puisse voir ce qu'il trace. On pourroit encor penser à d'autres moyens; le tout consiste dans le soin d'empecher que l'impulsion du stile même ne se mele avec la traction. Mais vous pourrés mieux choisir que personne. Lorsqu'on demande si cette construction est Geometrique il faut convenir de la desinition. Selon mon langage je dirois qu'elle l'est. Aussi crois ie que la description de la cycloide, ou de vos lignes faites par l'evolution¹²⁾, est Geometrique. Et je ne vois pas, pourquoy on restreint les lignes Geometriques à celles dont l'equation est Algebrique. Mais entre les constructions Geometriques ie prefere non seulement celles qui sont les plus simples mais aussi celles qui servent à reduire le probleme à un autre probleme plus simple et contribuent à éclairer l'esprit. Par exemple ie souhaiterois de reduire les quadratures ou les dimensions des aires aux dimensions des lignes courbes.

Mons. Bernoulli le ieune s'est plaint à son tour de M. le Marquis de l'Hospital, dans une lettre qu'il a voulu m'estre communiquée¹³⁾. Mais le suiet de leur contestation ne me paroist gueres considerable. Et la construction de la ligne de M: Beaune n'est pas de[s] plus difficiles. Aussi crois-ie qu'ils se seront raccommodés¹⁴⁾.

J'ay eu de la peine à me resoudre à chercher une des courbes dont vous me donnés les soutangentes, car ordinairement on s'engage en des calculs un peu longs, et maintenant je n'ose toucher à ceux qui sont tant soit peu prolixes. Neantmoins pour vous satisfaire, puisque vous m'aviés donné le choix, j'ay choisi la plus simple¹⁵⁾, qui est 2ayy:2aa-yy-xx¹⁶⁾, et j'ay trouvé que vous aviés raison de l'apeller un déguisement, car c'est le cercle à qui cette soutangente peut appartenir, et son equation est 2ax-xx=yy. Mais a fin que vous voyiés que j'ay approfondi ce probleme, et que ce n'est pas par quelque hazard que j'ay trouvé ce cercle, ie vous diray que la courbe n'est ordinaire, que dans ce

12) Les Développantes. Voir la ‘Definitio III’ de la ‘Pars Tertia’ de l'‘Horologium Oscillatorium’ où l'on lit, à propos d'une telle courbe: ‘Vocetur autem ea, Descripta ex evolutione’.

13) Probablement par l'intermédiaire de Otto Mencke, l'éditeur des ‘Acta Eruditorum’, par les mains duquel passa également la première lettre de Jean Bernoulli à Leibniz, du 20 décembre 1693.

14) Les lettres échangées à ce sujet entre de l'Hospital et Jean Bernoulli se trouvent à Stockholm dans la bibliothèque de l'Académie des Sciences, avec une grande partie de leur autre correspondance réciproque qui, sans doute, sera publiée un jour.

15) En marge de la lettre, Leibniz nota ici l'expression 2ayy/2aa-yy-xx.

16) Comparez la note 22 de la Lettre N^o. 2822.

[p. 542]

seul cas, mais transcendante dans une infinité d'autres. Ie vous en donneray premierement l'exemple le plus simple¹⁷⁾. Soit x=∫adv:a-v, (1) ou dx=adv::(a-v), (2) il est manifeste que la lettre x signifie une grandeur qui est comme le logarithme, posé qu' a - v soit le nombre. Car cela depend de la quadrature de l'Hyperbole ou de la description de la ligne Logarithmique. Cela posé, je dis que la ligne, dont l'equation est yy=aa+2ax-xx-av (3)¹⁸⁾, satisfait au probleme, et il est manifeste que cette ligne se peut construire, supposita Hyperbolae quadratura. Voicy comment ie prouve maintenant le succés par le calcul differentiel. Apres avoir differentié l'equation 3, je trouve 2ydy=2adx-2xdx--adv (4); dont ostant dv par l'equation 2 il y aura 2ydy=2adx-2xdx--adx+vdx(5). Et par cette derniere, jointe à l'equation 3 ostant v, il y aura enfin yydx=aadx+2axdx-xxdx-2aydy+2aadx-2axdx-aadx, ou bien, apres les destructions dûes: yydx+xxdx+2aydy=2aadx (6) ce qu'il falloit faire; car il est manifeste que dx:dy=2ay:, 2aa-yy-xx c'est à dire que la soustangente est 2ayy:, 2aa-yy-xx. La méme chose reussit dans une infinite d'autres lignes prenant l'arbitraire n, et disant: yy=na+2ax-xx-nv¹⁹⁾. Mais n estant egal à rien, il en provient le cercle. Quant aux ddx, j'en ay eu sou vent besoin elles sont aux dx, comme les conatus de la pesanteur ou les solicita tions centrifugues sont à la vitesse. M. Bernoulli marque dans les Actes de Leipzig de l'année passée p. 202 de les avoir employées pour les lignes des voiles²⁰⁾. Et ie les avois deiâ employées pour le mouvement des astres dans les mêmes actes²¹⁾. Au reste comme vous avés de la peine à souffrir, Monsieur, que ie pense souvent

17) Ici Leibniz note en marge: dx=adv/a-v.

18) On trouve à la page 85 du Livre J une construction très simple de cette courbe au moyen de la logarithmique. Ensuite Huygens y vérifie les calculs de Leibniz et il ajoute: ‘Hic novum est quod in aequatione curvae (3) sunt tres incognitae; quodque huic differentialem aequationem invenit (4). Ex qua deinde egregie eliminat dv, et v. Examinandae aliae curvae hoc modo compositae’.

19) Nous écririons: , solution correcte et générale de l'équation différentielle: y dx/dy=2ay²:(2a²-y²-x²).

20) Dans l'article en question, que nous avons cité dans la note 25 de la Lettre N^o. 2819, Jacques Bernoulli exprime comme il suit la propriété fondamentale de la courbe de la voile ‘Sumtis aequalibus curvae portiunculis, Cubi ex primis differentiis ordinatarum sunt proportionales secundis differentiis abscissarum’.

21) Dans ceux de février 1689; comparez la note 10 de la Lettre N^o. 2601.

[p. 543]

à l'Histoire au Droit et à la Politique, il y a bien des gens qui me font la guerre icy, et ailleurs de ce que ie me mêle des matieres ou vous regnés. En verité je m'accommoderois d'avantage de ce qui est de vótre goust, si j'en avois absolument le choix. Et j'estime plus les verités eternelles qui éclairent l'esprit que les faits ou les verités temporelles. Il faut cependant avouer, qu'encor en matiere de droit, de morale et de Politique on pourroit faire des decouvertes et des raisonnements exacts. Et souvent on y manque en practique, parce qu'on a coustume de les traitter superficiellement. Je seray bien aise de voir un jour vôtre jugement sur la preface de mon code diplomatique. Je vous avois communiqué mon proiect parce j'ay cru que peut estre quelque un de vos amis en Hollande me pourroit fournir quelque piece curieuse, dont il y en auroit sans doute qui seroient honorables à vostre Republique. Je n'employe que de pieces choisies. C'est pourquoy mon dessein n'est pas des plus vastes. Mais pour finir par nostre Geometrie, j'ose dire qu'on pousseroit peut-estre bien avant la recherche de ces choses, si on avoit à la main quelque ieune homme d'esperance, qui en s'instruisant nous pouvoit soulager dans le calcul. En attendant je fais ce que je puis pour meriter l'honneur que vous me faites de croire que ie suis avec tout le zele et toute la consideration possible,

Monsieur

Vostre treshumble et tres obeissant serviteur Leibniz.