De natuurkunde van 't vrije veld. Deel I

Licht en kleur in het landschap

[p. 73]

Het meten van lichtsterkte en helderheid.

45. De sterren als lichtbronnen van bekende sterkte.

De sterren vormen een natuurlijke reeks lichtbronnen van allerlei lichtsterkten. Met fotometers zijn deze zeer nauwkeurig gemeten en in grootteklassen uitgedrukt; de ‘grootteklasse’ m heeft dus niets te maken met de ‘grootte’ van de ster, maar alleen met haar lichtsterkte i.

m = grootteklasse	i = lichtsterkte in willekeurige maat	m	i
-1	251
0	100	0	100
1	39,8	0,1	91
2	15,8	0,2	83
3	6,31	0,3	76
4	2,51	0,4	69
5	1,00	0,5	63
6	0,40	0,6	58
7	0,16	0,7	53
		0,8	48
		0,9	44

Elke klasse is 2,51 maal zwakker dan de vorige. Op een constante na is i = 10^{0,4 m}.

In fig. 61 staan de grootteklassen aangegeven voor de sterren in de omgeving van de Grote Beer, die het gehele jaar te zien zijn. In fig. 62 staan de grootteklassen voor het schitterende wintersterrebeeld Orion. Ziehier nog enkele opgaven voor zeer bekende heldere sterren:

Sirius	= α Grote Hond	-1,3	Altaïr	= α Arend	1,1
Wega	= α Lier	0,3	Aldebaran	= α Stier	1,1
Capella	= α Voerman	0,3	Pollux	= β Tweelingen	1,3

[p. 74]

Arcturus	= α Bootes	0,2	Regulus	= α Leeuw	1,6
Procyon	= α Kleine Hond	0,6	Castor	= α Tweelingen	1,7

Voor andere sterren raadplege men een atlas, bv. Schurig-Götz, Tabulae Celestes.

De meeste mensen kunnen nog de 6e grootteklasse waarnemen, althans bij heldere nachten en ver van het licht der steden.

Fig. 61.

46. Uitdoving van het licht door de dampkring.

Nabij de gezichteinder zien we gewoonlijk maar zeer weinig sterren. Dat komt doordat de lichtstralen verzwakt worden bij hun weg door de lucht; stralen die bijna horizontaal verliepen hebben een veel langere weg afgelegd dan schuin invallende stralen, en worden dus sterker verzwakt.

Die verzwakking gaan we bepalen, zo mogelijk met behulp van een sterre-atlas, aangevuld met een lijst van grootteklassen; maar onze tabelletjes van § 45 zijn eigenlijk al voldoende, als Orion laag, en de Grote Beer hoog staan. De daar opgegeven

[p. 75]

Fig. 62.

[p. 76]

grootteklassen gelden voor 't geval dat de sterren hoog aan de hemel staan. Nu zoeken we een ster A, die niet ver van de gezichteinder staat, en vergelijken haar helderheid met die van de sterren om het Zenith (sterren hoger dan 45^o, die bijna niet verzwakt zijn). Zoveel mogelijk zoeken we sterren die precies gelijk zijn aan A of waar A tussenin ligt. Het verschil tussen de schijnbare grootteklasse van A en de ware grootteklasse volgens de tabellen, wordt opgetekend en bv. Δ genoemd; we bepalen ook nog de hoogte van de ster A op dit ogenblik (§ 235).

Als wij dit voor verschillende sterren op allerlei afstanden h boven de kim uitvoeren (een 10-tal is al voldoende om een eerste indruk te krijgen), komt er een tabelletje dat min of meer gelijken zal op het volgende:

h	Δ	Z	sec Z
90^o	0	0^o	1
45^o	0,09	45^o	1,41
30^o	0,23	60^o	2,00
20^o	0,45	70^o	2,92
10^o	0,98	80^o	5,73
5^o	1,67	85^o	11,4
2^o	3,10	88^o

Deze getallen der tweede kolom zijn gemiddelde waarden voor onze gewesten en voor zeer heldere lucht, maar ze veranderen van plaats tot plaats en vooral van nacht tot nacht.

In het tabelletje staat ook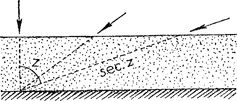

Fig. 63. Hoe schuiner de lichtstraal, hoe langer zijn weg door de dampkring.

de zenithsafstand Z = 90^o - h opgetekend, en sec Z, die aangeeft hoe lang de weg is die het licht door de dampkring heeft afgelegd (fig. 63). Zet nu uit: Δ tegen sec Z, dan vindt u een lijn die niet teveel van een rechte afwijkt; trek zo goed mogelijk tussen de waargenomen punten (fig. 64)! We zien dus uit deze tekening hoeveel grootteklassen de ster zwakker wordt naarmate de weg door de dampkring toeneemt. Het buitengewoon interessante van deze figuur is, dat men door de lijn te verlengen

[p. 77]

vinden kan hoeveel sterker de sterren zouden lijken als wij boven de luchtlaag die de Aarde omgeeft konden stijgen, nog hoger dan de stratosfeer! Een ster nabij het zenith zou 0,2 grootteklassen helderder worden, dit is ongeveer van 80 tot 100.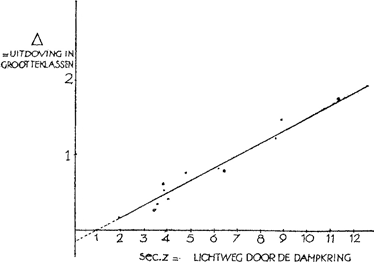

Fig. 64. Uitdoving Δ van het licht ener ster door de dampkring, bij verschillende zenithsafstand z.

We hebben dus bevonden dat de dampkring voor steil invallende stralen bijna ⅕ van het licht uitdooft; en dit geldt zowel voor de zon als voor de sterren. Die uitdoving is geen absorptie van het licht, maar verstrooiing, dezelfde verstrooiing waardoor de lucht blauw is (vgl. § 172).

47. Vergelijk een ster met een kaars.

Op een terrein met uitgestrekt, vrij uitzicht, bij nacht, vergelijken we de lichtsterkte van een kaars met die van een heldere ster, bv. Capella. Het is verrassend, hoe héél ver we ons van de kaars moeten verwijderen, wil haar helderheid afgenomen zijn tot die van de ster: op ongeveer 900 m is er gelijkheid. We krijgen dus van Capella een verlichtingssterkte van 1 / (900)² = 1/810.000 lux (vroeger: ‘meterkaars’).

De proef kan ook genomen worden met een zaklantaarn, maar dan zijn nog groter afstanden nodig. Stel het lampje boven op het dak van een huis of voor een torenraam!

Let op het kleurverschil!

[p. 78]

48. Vergelijk twee straatlantarens met elkaar.

Bij een avondwandeling merken we op dat we nu en dan twee schaduwen hebben, telkens nml. als we ons tussen twee lantarens bevinden. Naarmate we dichter bij de ene of bij de andere komen, wordt de ene of de andere schaduw zwarter. Waar de twee schaduwen even sterk zijn, krijgen we van beide lichtbronnen evenveel licht; uit de afstanden a en b volgt dan de verhouding der lichtsterkten: A / B = a² / b².

Bij vergelijking van gasgloeilicht met elektrische lampen is het verschil in kleur van de schaduwen opvallend.

49. Vergelijk de maan met een lantaren.

Zoek weer de twee schaduwen die deze lichtbronnen werpen: die tegenover de maan is roodachtig; die tegenover de lantaren, donkerblauw (vgl. § 96). We verwijderen ons van de lantaren: de maanschaduw blijft even sterk, maar de lantarenschaduw verbleekt; stel dat op 20 m van de lantaren beide gelijk zijn. De straatlantaren is een gewone, niet zeer sterke gloeilamp, ik schat: 50 kaars; op 20 m afstand is de verlichtingssterkte 50 / 20² = 0,13 lux. Dit moet dus tevens de verlichtingssterkte zijn die de volle maan teweegbrengt.

Vorige proef dachten wij ons bij volle maan. Herhaal ze bij eerste of laatste kwartier: de verlichtingssterkte is nu veel minder dan de helft; een aanzienlijk deel van het maansoppervlak is verduisterd door de schuine schaduwen der maanbergen (vgl. § 168)

Juiste waarden: volle maan ............. 0,20 lux,
eerste en laatste kwartier .. 0,02 lux.

50. Helderheid van de maanschijf.

Toen Herschel zijn reis naar Zuid-Afrika ondernam en zijn schip te Kaapstad aankwam, zag hij de bijna volle maan opgaan boven de Tafelberg, die beschenen was door de ondergaande zon. Het trof hem, dat de maan minder helder leek dan de rotsen, en hij besloot hieruit dat de maanoppervlakte uit donkere gesteenten moet bestaan.

Een dergelijke waarneming kunnen we in onze eigen omgeving doen, als we omstreeks 6 u. 's avonds de opgaande volle maan met een witte muur vergelijken, die door de ondergaande zon beschenen wordt. De afstanden zon - maan en zon - aarde zijn praktisch gelijk; als maan en muur uit dezelfde stof bestonden,

[p. 79]

zouden ze nu dezelfde helderheid moeten hebben, ook al zijn hun afstanden tot het oog nog zo verschillend (prachtige toepassing van een klassieke fotometrische stelling!). Het waargenomen verschil moet daaraan toe te schrijven zijn, dat de maan uit donkere gesteenten bestaat (lava?).

Wil deze waarneming zuiver zijn, dan moeten zon en maan even hoog boven de gezichteinder staan; hun licht wordt dan in dezelfde mate door de dampkring verzwakt.

51. Enkele helderheidsverhoudingen in het landschap.¹⁾

Helderheid zon = 300000 × helderheid van de blauwe lucht.

Helderheid van witte wolk = 10 × helderheid van de blauwe lucht.

Op een gewone zonnige dag met blauwe lucht komt 80% van het licht rechtstreeks van de zon, 20% van de hemel.

Verlichting op een horizontaal vlakje na zonsondergang, bij onbewolkte lucht²⁾;

stand der zon:	- 1^o	- 2^o	- 3^o	- 4^o	- 5^o	- 6^o
	250	113	40	13	5	2	lux.

Het oog past zich zo snel en goed aan alle verlichtingssterkten aan, dat wij ons geen voldoende rekenschap meer geven van de kolossale helderheidsverhoudingen die om ons heen voorkomen. Vergelijken wij eens een landschap verlicht door de volle zon, en een ander verlicht door de maan:

de zonneschijf zelf	100000 × 40000	de maanschijf	20000
een helderwit voorwerp	50000	een helderwit voorw.	0,25
roetzwart	1000	roetzwart	0,005

In éénzelfde landschap komen dus geen groter helderheidsverhoudingen voor dan ten hoogste 100:1; in absolute waarde verandert de verlichting echter ontzaglijk. Roetzwart in de zonneschijn is nog vierduizend maal helderder dan een wit papier bij volle maan!

1) Nela Research Lab. 1917, blz. 239 en 245. - Postma, Daylight measurements in Utrecht (Diss. 1936).

2) K. Kähler, Met. Zs. 44, 212, 1927.

52. Terugkaatsingsvermogen.

Je ziel is een groot water,
de sterren vinden geen beeld in jou.
Kurt Heynicke, ‘Ferne Frau’ (uit de bundel:
Rings fallen Sterne. Berlin, 1920).

Heeft u ooit de sterren in het water teruggekaatst gezien? In de stad lukt dit meestal niet, buiten wel, mits men kijkt in

[p. 80]

een plas of in een vijvertje bij windstil weer. Bij donkere nacht is die weerspiegeling een zeer mooi gezicht!

Heldere sterren van de 1e grootte, die nabij het zenith staan, ziet men zwak weerspiegeld, ongeveer als sterren van de 5e grootte. Een verschil van 4 grootteklassen komt overeen met een verhouding 40 ongeveer van de lichtsterkten: water weerspiegelt dus maar 2,5% van de loodrecht invallende stralen. Sterren die lager staan worden beter weerspiegeld.

Het terugkaatsend vermogen hangt samen met de brekingsaanwijzer, volgens de ‘formules van Fresnel’. Voor loodrechte inval is het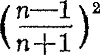



. In de tabel is grafisch het terugkaatsend vermogen voorgesteld van glas en van water, onder verschillende hoeken i met de normaal spiegelend.

We begrijpen nu ook waarom we in de stad geen sterren weerspiegeld zien: de hemel is hier niet donker genoeg, sterren van de 3e grootte zijn al nauwelijks meer zichtbaar; daarenboven is het wateroppervlak zelf teveel verlicht. Alleen planeten zijn nog wel zichtbaar, als ze veel helderder zijn dan de 1e grootte.

Bij dag schijnen de teruggekaatste blauwe hemel, de huizen en de bomen, veel lichtsterker dan 2%; op sommige schilderijen ziet men nauwelijks verschil tussen de helderheid van de voorwerpen en die van hun spiegelbeeld. Dit is eenvoudig gezichtsbedrog.

Er is een volksgeloof, dat sterren niet weerspiegeld worden door diepe wateren. Dit mist natuurlijk elke redelijke grond.

		Terugkaatsingsvermogen
invalshoek i		van water		van glas (n = 152)
0		0,020		0,043
10		0,020		0,043
20		0,021		0,043
30		0,022		0,043
40		0,024		0,049
50		0,034		0,061
60		0,060		0,091
70		0,135		0,175
	75		0,220		0,257
80		0,350		0,388
	85		0,580		0,615
90		1,000		1,000

[p. 81]

53. Doorlating van metaalgaas.

Voor het dragen van lichtreklames zijn soms metaalconstructies op de daken opgesteld en met metaalgaas bespannen. Van verre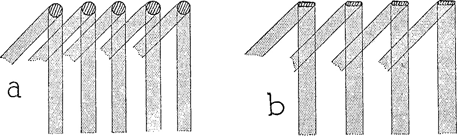

Fig. 65. Doorlating van metaalgaas, gezien vanuit twee verschillende richtingen a. het gaas bestaat uit draden met ronde doorsnede; b. het gaas bestaat uit platte bandjes.

ziet men de afzonderlijke draden niet meer, het gaas lijkt een gelijkmatig verzwakkende plaat grauw glas. Het is belangwekkend, het gaas van uit toenemend schuine richtingen te bekijken: het wordt dan steeds donkerder.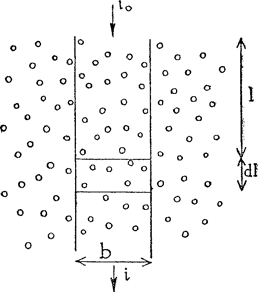

Fig. 66. We berekenen hoeveel licht er tussen de stammen van een bos nog te zien is.

Dit is een bewijs dat het uit draden met ronde doorsnee bestaat; was het uit platte bandjes opgebouwd, dan zou het onder elke hoek even donker blijven (fig. 65).

54. De ondoorzichtigheid van een bos.

Zolang een bos zich slechts over een geringe diepte uitstrekt, zien we in de verte de lichte lucht tussen de stammen door. Klaarblijkelijk moet er een eenvoudige betrekking zijn die aangeeft welk gedeelte van het licht nog ongehinderd doorgelaten wordt, als wij aannemen dat de bomen volgens het toeval verdeeld zijn, dat er N bomen per m² voorkomen, en dat zij op ooghoogte een middellijn D hebben.

[p. 82]

Beschouw immers een bundel lichtstralen van breedte b, die al een lengte l door het bos heeft doorlopen (fig. 66). Van de oorspronkelijke lichthoeveelheid i₀ is nog i over. Als de lichtstralen nog over een kleine afstand dl verder lopen, wordt weer een kleine hoeveelheid di van het licht weggenomen, en wel is
di/i = - dl . b . N . D / b = - dl ND.
Hieruit volgt door integratie:
i = i₀ . e^-NDl = i₀ . 10^{-0,43 NDl}

Er wordt dus minder en minder licht doorgelaten naarmate het bos dieper wordt, juist zoals door een donkere vloeistof minder en minder licht gaat naarmate de laag dikker wordt.

Stel voor een dennebos N = 1 per m²; D = 0,10 m. Dan vinden we ongeveer:

l = 10 m	i / i0 = 0,37
l = 25 m	0,10
l = 50 m	0,01
l = 70 m	0,001

Men ziet hoe snel de ondoorzichtigheid toeneemt. Uit een ruwe schatting van het breukdeel van de gezichteinder dat nog door de bomen vrijgelaten wordt, volgt de diepte van het bos.

Welke waarde heeft ND bij beukebos? Bij jong en oud dennebos?

55. Zwevingen tussen twee hekken.

Overal waar men twee hekken, het ene door het andere heen ziet, bemerkt men brede lichte en donkere golvingen in de lichtsterkte, die verlopen zodra men zich beweegt. - Zij ontstaan natuurlijk, doordat de (schijnbare) afstand der staven van elkaar enigszins verschillend is voor de twee hekken, hetzij omdat het éne grover is dan het andere, hetzij doordat ze zich verschillend ver van ons oog bevinden. In bepaalde richtingen schijnen de staven dan ongeveer samen te vallen, in andere vullen de staven van het eerste hek juist de tussenruimten van het andere; zodat er een verschil in de gemiddelde helderheid ontstaat (‘in step’ - ‘out of step’).

Heeft men die zwevingen eenmaal opgemerkt, dan ziet men ze op allerlei plaatsen. Elke brug die aan haar beide kanten een hekvormige borstwering draagt, vertoont die helderheidsgolvingen zodra men ze van op een zekere afstand bekijkt. Ze verschijnen ook, als men dwars door een hek de schaduw van datzelfde hek ziet: de periode is dezelfde, maar de afstand tot ons oog is

[p. 83]

verschillend. In sommige stations is er metaalgaas om de goederenlift aangebracht: de naar ons toegekeerde zijde en de van ons

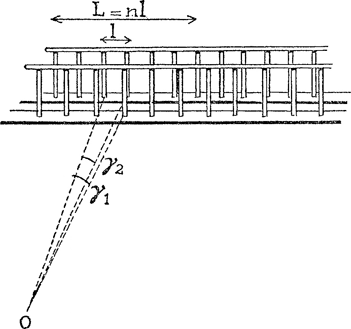Fig. 67. Zwevingen tussen twee hekken.

afgekeerde zijde vormen samen een soort moiré, hetzelfde dat men ook opmerkt als men twee stukken metaalgaas op elkaar legt, of twee kammen van ongelijke tandafstand. Beschouw nauwkeuriger het eenvoudige geval (fig. 67), waarin wij twee gelijke hekken op ongelijke afstanden x₁ = OA en x₂ = OB van ons oog zien; stel l de afstand tussen twee opeenvolgende staven, die we zien onder gezichtshoeken



en



. De lengte ener zwevingsgolf omvat een aantal staven n, gegeven door



; dus des te meer naarmate we ons verder van de hekken verwijderen. Daarentegen is de hoek Θ waaronder we een zwevingsgolf zien altijd dezelfde, want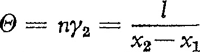



. De ware lengte



ener zwevingsgolf kunnen we bepalen, door evenwijdig aan het hek te lopen: de zwevingsgolven verplaatsen zich met een snelheid, gelijk aan de onze; meet hoever u moet lopen opdat de ene golving nauwkeurig de plaats schijne in te nemen van de vorige. - Onderzoek of elk van die betrekkingen uitkomt. Of andersom, uit de bepalingen van n, Θ, L haalt men de waarden van x₂, x₂ - x₁ en l, en kan aldus zonder enig instrument alle afmetingen van op afstand bepalen.

[p. 84]

Als de twee hekken een verschillende periode hebben, zien we bij elke beweging van ons oog de zwevingsgolven op de merkwaardigste wijze verlopen; soms in dezelfde richting waarin wij

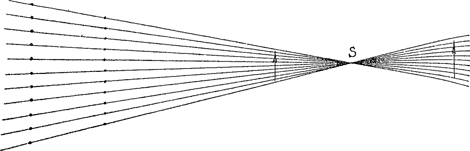Fig. 68. Zwevingen tussen twee hekken van verschillende periode.

ons verplaatsen, soms in de tegengestelde, naarmate wij ons vóór of achter het ‘uitstralingspunt’ S bevinden (fig. 68); met andere woorden: naarmate γ₁ < γ₂ of γ₁ > γ₂. De zwevingen verplaatsen zich sneller en sneller als we tot S naderen.

Fig. 69. Zwevingen tussen een hek en de schaduw daarvan. a. waarnemingsomstandigheden b. vorm der zwevingsgolven.

Als een vertikale omheining haar schaduw werpt op een horizontaal terrein, zien de zwevingen er ietwat anders uit (fig. 69); boven liggen ze dichter bij elkaar, onder zijn ze verder van elkaar verwijderd; daarenboven is er een geringe kromming in te onderkennen. Inderdaad klopt dit met de vorige beschouwingen: de afstand tussen de twee interfererende hekfiguren is boven het grootst, wij zien hun periode dus onder een zeer verschillende hoek, en de zwevingen liggen dicht bij elkaar; onderaan is het omgekeerd.

[p. 85]

56. Fotografische fotometrie.¹⁾

In alle fotografie-winkels kan men ‘daglichtpapier’ kopen, dat in de zon snel een bruinpaarse kleur aanneemt. Ruw kan men zeggen dat de tijd, nodig opdat het papier een bepaalde kleur zou bereiken, omgekeerd evenredig is met de lichtsterkte die op het papier valt (‘regel van Bunsen - Roscoe’). Als men dus altijd met hetzelfde papier werkt, en eens en vooral een stukje gewoon bruinpaars papier als ‘normaaltint’ heeft gekozen, kan men gemakkelijk overal lichtsterkten bepalen: men neemt eenvoudig op hoeveel tijd er nodig is opdat het lichtgevoelige papier de normaaltint zou aannemen. Het normale papier moet zo weinig mogelijk aan het licht blootgesteld worden, om verbleken te vermijden. Onze normale tint kiezen we met zorg. We houden een reepje daglichtpapier in de zon, en dekken er achtereenvolgende trapjes van af, resp. na 10, 20, 40, 80, 160, 320, 640 sekunden; na afloop bekijken wij het papiertje bij zwak licht; de eerste trappen en de laatste vertonen weinig kontrast, de middenste zijn het gunstigst. Kies als normaal een blad papier (boekband, reklameplaat, ....) dat goed effen van kleur is en zo nauwkeurig mogelijk dezelfde tint heeft als een der middenste trapjes; is de kleurtoon niet volmaakt dezelfde, dan moet u bij het vergelijken eer letten op de helderheid, en die met half gesloten ogen beoordelen. - Merk op, dat we ons daglichtpapier noch ontwikkelen noch fixeren, de gebruikte reepjes kunnen niet bewaard worden.

Op deze wijze heeft Wiesner tal van onderzoekingen over het lichtklimaat uitgevoerd, waaronder de verschillende planten zich ontwikkelen. Hoe ruw de methode ook zij, het is heerlijk om aldus snel, op een groot aantal plaatsen en in allerlei omstandigheden, een schatting te krijgen van een grootheid waarvan zelfs de orde ons niet bekend was!

Onderzoek de belichting van een horizontaal vlak bij verschillende zonshoogte.

Vergelijk de verlichting op een horizontaal vlak bij zonneschijn:

a. als een schermpje er schaduw op werpt; b. zonder schermpje; vergelijk aldus het licht dat direkt van de zon komt met dat welk door de blauwe hemel wordt uitgezonden.

Vergelijk de verlichting van een naar beneden en een naar boven gekeerd vlak: boven water is de verhouding 6, boven grint 12, boven gras 25.

1) J. Wiesner, Der Lichtgenuss der Pflanzen (Leipzig, 1907).

[p. 86]

Vergelijk de helderheid van de blauwe lucht in verschillende richtingen, door verscheiden, even grote kokers onder verschillende hoeken op te stellen, en fotografisch papier op de bodem te leggen. Gewoonlijk blijkt de lucht het donkerst op 90^o van de zon (vgl. § 176).

Vergelijk de verlichting in een bos en daarbuiten (tenminste 20 m van de bosrand blijven!).

Vergelijk de verlichting in een beukebos a. midden Mei; b. bij het ontplooien der eerste bladeren; c. begin Juni. In een bepaald geval vond men 1/11, 1/30, 1/64 t.o.v. de verlichting buiten het bos.

Meet de verlichtingssterkte op groeiplaatsen van:

weegbree (Plantago major)	1
klimop (Hedera helix)	1 tot 0,22 (bloeiend)
	1 tot 0,02 (onvruchtbare takken).
heidekruid (Calluna vulgaris)	1 tot 0,10
adelaarsvaren (Pteridium aquilinum)	tot 0,02

Bepaal de verlichtingssterkte binnen in boomkruinen: dit is ongeveer de kleinste verlichtingssterkte waarbij zich nog twijgen kunnen ontwikkelen. Voor vrijstaande bomen werd gevonden: lork 0,20; berk 0,11; grove den 0,10; spar 0,03; beuk 0,01 (alles t.o.v. de verlichting buiten de boom).