Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente
(1950)–Christiaan Huygens–
[pagina 204]
| |
Appendice I
| |
[pagina 205]
| |
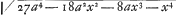 . Porro quoniam est BE ∞ a, et ED ∞ 3a, erit EC ∞ √a4 [lisez: EC ∞ √3a2] et rectangulum DEC ∞ √27a4. Unde manifestissime apparet rectangulum DEC ipsum DGH superare, nempe illius DEC quadratum quadratum hujus DGH 18aaxx+8ax3+x4. Ideoque rectangulum DEC maximum. - Caeterum sit punctum G inter E et D, ac rectangulum Dgh ipso DEC . Porro quoniam est BE ∞ a, et ED ∞ 3a, erit EC ∞ √a4 [lisez: EC ∞ √3a2] et rectangulum DEC ∞ √27a4. Unde manifestissime apparet rectangulum DEC ipsum DGH superare, nempe illius DEC quadratum quadratum hujus DGH 18aaxx+8ax3+x4. Ideoque rectangulum DEC maximum. - Caeterum sit punctum G inter E et D, ac rectangulum Dgh ipso DEC
 majus; ponatur iterum Eg ∞ x, eritque Bg ∞ a+x, gD ∞ 3a-x, et gh ∞ 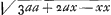 , adeoque rectangulum Dgh ∞ , adeoque rectangulum Dgh ∞ 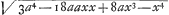 , et quoniam a semper major est quam x (nam si minor esset, demonstrationem ab alterâ parte diametri inciperem) erit etiam aaxx major quam ax3, ideoque 18aaxx multo majus quam 8 ax3; Quare facile patet √27a4 sive rectangulum DEC majus esse quam , et quoniam a semper major est quam x (nam si minor esset, demonstrationem ab alterâ parte diametri inciperem) erit etiam aaxx major quam ax3, ideoque 18aaxx multo majus quam 8 ax3; Quare facile patet √27a4 sive rectangulum DEC majus esse quam 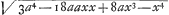 sive rectangulum Dgh, hoc est, cum punctum g sive G utcunque assumpta sint, majus quam caetera omnia rectangula, quae eodem modo in ipso semicirculo describi possunt. Ideoque si in quocunque semicirculo radius sive semidiameter bifariam dividatur, et ex ipso puncto ad peripheriam perpendicularis erigatur, erit rectangulum sub majori abscissâ parte diametri, et applicatâ contentum, maximum eorum omnium, quae eodem modo in ipso semicirculo describi possunt, quod demonstrandum erat. sive rectangulum Dgh, hoc est, cum punctum g sive G utcunque assumpta sint, majus quam caetera omnia rectangula, quae eodem modo in ipso semicirculo describi possunt. Ideoque si in quocunque semicirculo radius sive semidiameter bifariam dividatur, et ex ipso puncto ad peripheriam perpendicularis erigatur, erit rectangulum sub majori abscissâ parte diametri, et applicatâ contentum, maximum eorum omnium, quae eodem modo in ipso semicirculo describi possunt, quod demonstrandum erat.
Ce qui précède peut être considéré comme un Lemme. Datâ curvâ BCM cujus vertex B, axis BN, quaeque ejus est proprietatis ut quadratum parametri AB ductum in interceptam quamlibet axis partem, ut in BE, aequale sit cubo applicatae, ut EC (describitur autem ea curva geometrice motu et intersec- | |
[pagina 206]
| |
tione iisdem, quibus Parabola describi Cap. 4. Lib. 1. Elem: Curvar: demonstratum estGa naar voetnoot1), dummodo loco anguli, qui ibidem exprimitur per EBH, assumatur Parabola quaelibet, cujus axis sit in rectâ, quae illic exprimitur per BE, et vertex in puncto, quod ibidem designatur per B, ita ut loco rectae, quae ibi est BH succedat curva Parabolae
 assumptae:) invenire BD axis partem ejusdem longitudinis ut descripto super eâ semicitculo, maximum in eo rectangulum, contentum sub parte diametri a D versus B interceptâ, et sub applicatâ nempe DEC rectangulum, aequale sit quadrato parametri, qui quidem descriptus circulus datam curvam, ut postea demonstrabitur, tanget in C; ac praeterea ex centro ipsius circuli ad curvam ducere rectam iK, quae sit maxima earum omnium, quae ex i inter B et C, ad eandem curvam duci possunt. | |
[pagina 207]
| |
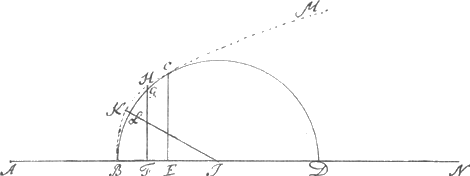
Ponamus rem omnino factam, nempe BCD esse circulum quaesitum, et maximum in eo rectangulum DEC, eritque BE quadrans diametri, et cum ED in ratione tripla ut supra demonstratum est. Porro sit latus rectum ∞ a, et BE ∞ x, erit ED ∞ 3x, et EC ∞ √3xx, ideoque rectangulum DEC ∞ √27x4 ∞ aa quadrato Parametri, sive 27x4 ∞ a4, et x4 ∞ a/27, adeoque x ∞ 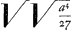 . Fiat igitur BE ∞ . Fiat igitur BE ∞ 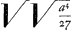 et ED ∞ 3 et ED ∞ 3 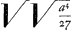 , sive , sive 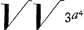 , describaturque super BD circulus; dico, erectâ ex puncto E perpendiculari EC, circulum secante in C, maximum in eo rectangulum DEC (quia BE et ED in ratione triplâ sunt ut supra demonstratum est) aequale esse quadrato parametri, et praeterea eundem circulum datam curvam tangere in eodem puncto C. Etenim cum rectangulum DEC aequale sit AB quadrato, erit DEC in EB, seu DEB in EC id est cubus ex EC aequalis quadrato AB in EB, ideoque punctum C in curva. Porro sumpto in peripheriâ BCD alio utcunque puncto G, applicataque GF, quae curvam secet in H, erit ex constructione DFG rectangulum minus rectangulo DEC, hoc est quadrato AB, ideoque et DFG in BF, seu DFB in FG, hoc est cubus ex FG minor quadrato AB in BF, hoc est cubo ex FH, adeoque et recta FG minor quam recta FH, et per consequens punctum G in peripheria BCD, praeter B et C utcunque assumptum, id est caetera omnia peripheriae BCD puncta intra curvam: unde
patet circulum BCD curvam tangere in puncto C. Denique quoniam BE ∞ est , describaturque super BD circulus; dico, erectâ ex puncto E perpendiculari EC, circulum secante in C, maximum in eo rectangulum DEC (quia BE et ED in ratione triplâ sunt ut supra demonstratum est) aequale esse quadrato parametri, et praeterea eundem circulum datam curvam tangere in eodem puncto C. Etenim cum rectangulum DEC aequale sit AB quadrato, erit DEC in EB, seu DEB in EC id est cubus ex EC aequalis quadrato AB in EB, ideoque punctum C in curva. Porro sumpto in peripheriâ BCD alio utcunque puncto G, applicataque GF, quae curvam secet in H, erit ex constructione DFG rectangulum minus rectangulo DEC, hoc est quadrato AB, ideoque et DFG in BF, seu DFB in FG, hoc est cubus ex FG minor quadrato AB in BF, hoc est cubo ex FH, adeoque et recta FG minor quam recta FH, et per consequens punctum G in peripheria BCD, praeter B et C utcunque assumptum, id est caetera omnia peripheriae BCD puncta intra curvam: unde
patet circulum BCD curvam tangere in puncto C. Denique quoniam BE ∞ est 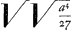 , et ED ∞ √√3a4, erit EC ∞ √⅓aa, adeoque rectangulum maximum DEC (ut supra demonstratum est:) ∞ √√a8, sive aa, aequale quadrato parametri: quod faciendum et demonstrandum erat.
Porro ad ducendam rectam lineam a puncto i, praedicti circuli centro, ad curvam, quae maxima earum omnium est quae ex eodem puncto ad ipsam curvam inter B et C duci possunt, rursus supponamus rem factam, et iK eandem maximam esse, sitque iterum Parameter ∞ a, applicata KL vero ∞ x, et quoniam BE ∞ , et ED ∞ √√3a4, erit EC ∞ √⅓aa, adeoque rectangulum maximum DEC (ut supra demonstratum est:) ∞ √√a8, sive aa, aequale quadrato parametri: quod faciendum et demonstrandum erat.
Porro ad ducendam rectam lineam a puncto i, praedicti circuli centro, ad curvam, quae maxima earum omnium est quae ex eodem puncto ad ipsam curvam inter B et C duci possunt, rursus supponamus rem factam, et iK eandem maximam esse, sitque iterum Parameter ∞ a, applicata KL vero ∞ x, et quoniam BE ∞ 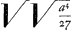 , ac ED ∞ √√3a4, erit BD ∞ , ac ED ∞ √√3a4, erit BD ∞ 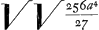 , adeoque Bi ∞ , adeoque Bi ∞ 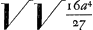 , et LB ∞ x3/aa. Li vero ∞ , et LB ∞ x3/aa. Li vero ∞ 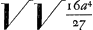 -x3/aa, unde cum Li quadratum cum quadrato LK aequale sit quadrato Ki, erit -x3/aa, unde cum Li quadratum cum quadrato LK aequale sit quadrato Ki, erit 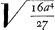 +x6/a4-2x3/aa in +x6/a4-2x3/aa in 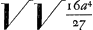 +xx ∞ quadrato alicujus maximi, quae sit z, nempe ∞ zz, sive x6/a4-2x3 +xx ∞ quadrato alicujus maximi, quae sit z, nempe ∞ zz, sive x6/a4-2x3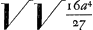 /aa+xx+ /aa+xx+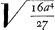 -zz ∞ 0. -zz ∞ 0.
| |
[pagina 208]
| |
sive x6-2a3x3 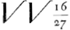 +a4xx+a6 +a4xx+a6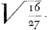 -a4zz. Quae aequatio, cum duas aequales radices habeat, multiplicanda est per Arithmeticam progressionem, secundum D. Huddenii regulam, ut sequitur: -a4zz. Quae aequatio, cum duas aequales radices habeat, multiplicanda est per Arithmeticam progressionem, secundum D. Huddenii regulam, ut sequitur:
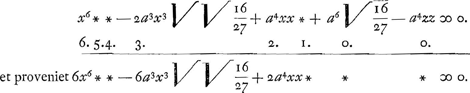 sive x4 * *-a3x 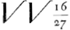 +⅓a4 ∞ 0. Caeterum ut signum radicale ex aequatione auferatur, sit y ∞ x√√3, eritque x ∞ y/√√3, quo substituto loco ipsius x, et ejusdem quadratoquadrato loco x4, habebitur +⅓a4 ∞ 0. Caeterum ut signum radicale ex aequatione auferatur, sit y ∞ x√√3, eritque x ∞ y/√√3, quo substituto loco ipsius x, et ejusdem quadratoquadrato loco x4, habebitur
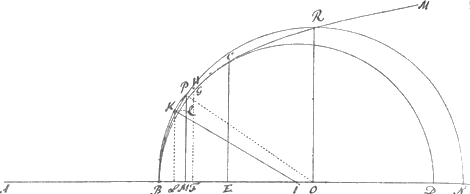
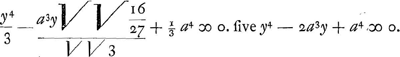 Unde aequationis solutio per datam curvam, ac proinde maxima earum omnium quae ex puncto i inter B et C, ad curvam duci possunt, facile perspicua est: etenim si fiat BO in axe aequalis parametro, centroque O, intervallo vero ejusdem OB circulus describatur, secans curvam in P et R, prima tantum ad solutionem aequationis utilis erit, quia altera in ipsius circuli centro cadet, cum parametro aequalis sit; Quare igitur si fiat PM ad MQ, sicut DE ad AB, id est ut √√3 ad 1, ductaque QK ipsi BO parallela, curvam secante in K, jungatur iK, eadem iK maxima earum omnium erit, quae ex i ad curvam inter B et C duci possunt. Cum enim AB sive BO sit a, si ponatur PM ∞ y, erit BM ∞ y3/aa, et MO ∞ a-y3/aa, est vero quadratum MO una cum quadrato MP, aequale quadrato OP seu OB, quare erit y6/a4-2y3/a+aa+yy∞aa sive y4-2a3y+a4 ∞ 0, et patet PM ∞ esse y ex aequatione y4-2a3y+a4 ∞ 0. Verum enimvero quoniam y∞x√√3 posita fuit, erit eadem y ad x sicut √√3 ad unitatem, est autem ex constructione PM ad MQ, sive ad LK, pro quâ x primo posita fuit, sicut √√3 ad 1: manifestum est igitur ipsam MQ fore ∞ x ex aequatione x4-a3x 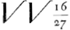 +⅓a4 ∞ 0, adeoque Ki maximam earum omnium, quae ex puncto i ad datam curvam inter B et C duci possunt, quod faciendum ac demonstrandum erat. +⅓a4 ∞ 0, adeoque Ki maximam earum omnium, quae ex puncto i ad datam curvam inter B et C duci possunt, quod faciendum ac demonstrandum erat.
| |
[pagina 209]
| |
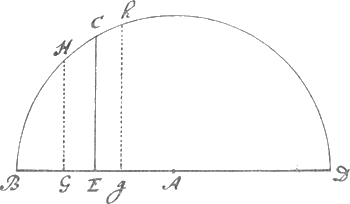
La deuxième feuille a le texte suivant (également d'une main étrangère, comme nous l'avons dit): Curva BCM, cujus vertex B, diameter BN, ejus est proprietatis ut quadratum parametri AB, ductum in interceptam quamlibet diametri partem, ut in BE, aequale sit cubo applicatae ut EC; Describitur autem ea curva geometrice motu et intersectione iisdem, quibus Parabolam describi, Cap. 4. Lib 1 Elem: Curv. demonstratum est, dummodo loco anguli, qui ibidem exprimitur per EBH, assumatur ParabolaGa naar voetnoot2) quaelibet, cujus axis sit in rectâ, quae illic exprimitur per BE, et vertex in puncto, quod 'bidem designatur per B, ita ut loco rectae, quae ibi est BH, succedat curva Parabolae assumptae. Demonstrandum curvam BHCM, supra expositam, per Circuli peripheriam in sex diversis punctis secari posse. Sumptâ BD diametri parte ejus longitudinis, ut descripto super eâ circulo BCD, maximum in eo rectangulum contentum sub parte diametri a D versus B interceptâ et sub applicatâ, nempe DEC rectangulum aequale sit quadrato parametri AB. Dico primum punctum peripheriae non B solum, sed et C esse in curvâ expositâ; Etenim, cum DEC aequale sit AB quadrato, erit DEC in EB, seu DEB in EC, id est cubus ex EC, aequalis quadrato AB in BE, ideoque punctum C in curvâ. Dico porro caetera | |
[pagina 210]
| |
omnia peripheriae BCD puncta cadere intra curvam BHCM: Sumpto enim in peripheria BCD alio utcunque puncto G, applicataque GF, quae curvam secet in H, erit ex constructione rectangulum DFG minus rectangulo DEC hoc est quadrato AB, ideoque et DFG in BF, seu DFB in FG, hoc est cubus ex FG minor quadrato AB in BF, hoc est cubo ex FH, adeoque et recta FG minor quam recta FH, et per consequens punctum G in peripheria BCD, praeter B et C utcunque assumptum, id est caetera omnia peripheriae BCD puncta intra curvam. Ducta itaque ex circuli BCD centro I ad curvam recta IK, maxima earum omnium, quae ex I inter B et C ad curvam duci possunt, quae secet peripheriam in L. Manifestum est circulos omnes centro I, ac quolibet intervallo majore quam IL, minore vero quam IK descriptos pluresque alios curvam BCM in sex diversis punctisGa naar voetnoot3) secare. Non hic adjectum est quo pacto geometrice inveniatur longitudo BD, ita ut omnium, quae in semicirculo DCB modo supra expresso, fieri possunt, rectangulorum maximum (ut DEC) aequale sit quadrato AB; nec etiam qua proportione secanda sit circuli diametro uti hic factum in E, ut rectangulum sub majori parte et applicata velut hic DEC, sit omnium similium in eodem circulo rectangulorum maximum, ut nec qua methodo maxima IK ducatur. Quoniam haec omnia Geometris obvia sunt, nec vis demonstrationis ex hisce dependet.
Demonstratum Operâ et studio Dom: Joan: de Witt. Huygens ajoute ce qui suit.Si AB vocetur a, BI debet esse 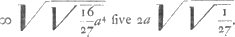 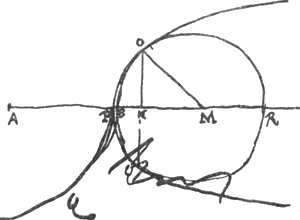 Et IE ∞ ½ BI. C'est exact, comme on peut aisément le vérifier. | |
[pagina 211]
| |
Si sumatur BM ∞ 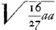 , quae minor est quam BI. Et BN ∞ ¼ BM, deinde applicetur ordinatim NO, et centro M, radio MO circumferentia describatur OPQR; haec curvam BO in puncto O simul tangit et secat. , quae minor est quam BI. Et BN ∞ ¼ BM, deinde applicetur ordinatim NO, et centro M, radio MO circumferentia describatur OPQR; haec curvam BO in puncto O simul tangit et secat.
Nous ne voyons pas comment Huygens a obtenu ce résultat, mais nous avons vérifié que c'est bien pour le point de la courbe indiqué par lui que le centre de courbure, ou centre du cercle osculateur, tombe sur l'axe des x, l'équation de la courbe étant a2x=y3. |
|


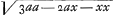 , adeoque rectangulum DGH ∞
, adeoque rectangulum DGH ∞