Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente

[p. 112]

LXVI
Ph. de la Hire à Christiaan Huygens.
[1678 ou 1679?]¹⁾.

Portefeuille anonyme.

Propositio 40. 3^tii Lib. Coni. de la Hire.

Sint Sectiones oppositae AB, IM quarum Asymptoti CE, CD suntad rectosangulos: in alterutra sumpto puncto A, et ductâ AF aequidistante Asymptoto CE, bisectâ AF in H et ad libitum productâ HO perpendiculari ad AF; descripto circulo BAFIM cujus centrum sit in recta HO, et radius OA uel OF, si circulus occurrat sectioni AB in aliquo puncto B diuerso ab A, et sectioni oppositae duobus in punctis IM ductis BG, IP, MN parallelis Asymptoto CE.

Dico summam IP, MN esse aequalem BG.

Sed si circulus occurrat sectioni MI in unico puncto I. Dico duplam IP esse aequalem BG.

Tandem si circulus contingat sectionem BA in A, erit AF aequalis summae IP, MN, uel in secundo casu aequalis duplae IP.

Productis BA, MI et iunctis BM, AI, ductisque BR, IS parallelis CD; per 13 prop. 2ⁱ huius aequales erunt EB, AD; ZM, IL; MV, XB; IQ, AT, quare ER aequalis est AF, similiter QS aequalis AF; sunt ergo ER, QS aequales; proptereadem erunt RX, MN aequales, et SL, MN aequales; aequales igitur RX, SL; et EX, QL.

Ductâ QY parallela ED et LY parallelâ MB erit triangulum QYL simile similiterque positum et aequale triangulo EBX; et recta YS parallela CD in directum occurret rectae IS, et simul constituent rectam lineam IY.

Propter circulum BAIM et parallelas QY, LY rectis ED, MB erunt anguli QIL,

1) La date est incertaine. Il nous semble toutefois probable que de la Hire ait communiqué les présents théorèmes à Huygens avant le départ de ce dernier de Paris en 1681. Voyez sur les publications de de la Hire les p. 220-221 du T. XX. Mais nous ne connaissons aucun ‘Liber Conicorum’ de lui qui contienne les propositions du texte. Il semble d'après les paroles de l'auteur que ce ‘liber meus’, apparemment écrit en latin, était achevé. N'a-t-il pas vu le jour? Il ne s'agit pas des ‘Sectiones conicae in novem libros distributae’ de 1685.

[p. 113]

QYL simul aequales duobus rectis, quamobrem quadrilatero QILY circulus circonscribi potest cum anguli oppositi sint aequales duobus rectis, quare angulus QYS aequalis angulo EDC aequalis est angulo ZLC.

Iam si hyperbola MI cum recta ZMIL erit parallela ED quare per 18 prop. huius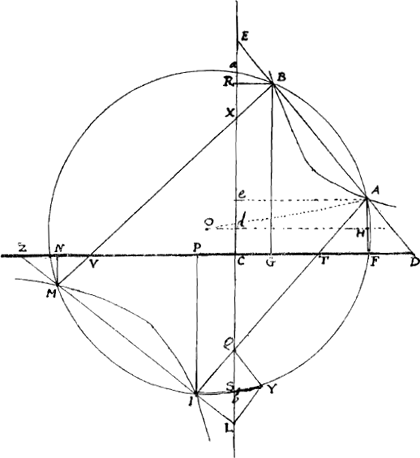



rectangulum EA in AD uel EB erit aequale rectangulo LM in MZ uel LI: sed propter circulum rectangulum EB in EA aequale est rectangulo Eb in Ea et rectangulum LI in LM aequale est rectangulo La in Lb, quare rectangulum Ea in Eb aequale est rectangulo La in Lb quamobrem Ea, Lb sunt aequales: sed per constructionem circuli diameter HO bisecat chordam ab in d, erit igitur Ed aequalis Ld; sed EX aequalis est LQ; ergo dX aequalis est dQ; et ductâ Ae parallela DC erit de aequalis dC, et eX aequalis CQ. cum sint: LS aequalis RX, SQ aequalis AF uel eC, et CQ aequalis eX

[p. 114]

erit LC aequalis RC vel BG, sed per 38 huius IP cum MN aequalis est LC ergo IP cum MN aequalis est BG. quod erat propositum.

Pro caeteris casibus erit fere eadem demonstratio quod fusius in libro meo traditum est sed haec tibi sufficient uir Illustrissime. addam tamen propos. 38 hujus libri insupra allatam demonstrationem omnino necessariam.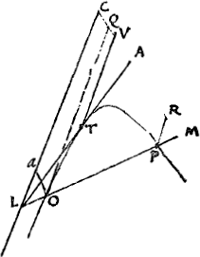

Propositio 38.3^tii Libri Coni.

Esto hyperbola OTP cuius Asymptoti CL, CM et centrum C, sumpto puncto L in utrouis Asymptoto, et ductis rectis LA contingente in T et LM occurrente in O et P hyperbolae a punctis O, P, T ductis parallelis OQ, TV, PR Asymptoto in quo sumitur punctum.

Dico summam OQ, PR esse aequalem duplo TV.

Per 13 prop. libri. 2ⁱ. huius LO aequalis est PM et ductâ Oa parallela CM erit PR aequalis La quamobrem PR cum OQ aequalis est LC, sed per 12 prop. eiusdem LA bisecatur in T quare dupla TV aequalis est LC, erit igitur OQ cum PR aequalis duplae TV. quod erat propositum.

In propositione 39 idem demonstravi in sectionibus oppositis.