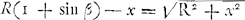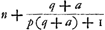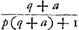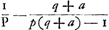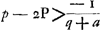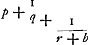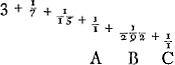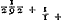Oeuvres complètes. Tome XXI. Cosmologie
(1944)–Christiaan Huygens–
[pagina 587]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 588]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Description du planétaire.C'est de nos jours seulement, me semble-t-il, que l'on a acquis une connaissance définitive et parfaite des choses célestes, quoique l'astronomie soit déjà née il y a deux mille ans et ait été cultivée dès lors par des esprits éminents: c'est dans la dernière centaine d'années, pour être plus précisGa naar voetnoot1), qu'on y a fait plus de progrès que dans tout le reste du temps. En effet, nous n'avons pas seulement appris à faire beaucoup mieux et plus simplement ce qui constituait jadis le but principal des recherches, savoir déterminer les lieux des astres tant fixes qu'errants, établir les longueurs de l'année et des mois, et prédire les éclipses; mais nous sommes de plus, ce qui est plus important et plus glorieux, possesseurs d'une science certaine sur l'ordre, la position, la proportion et la figure des orbes célestes suivant lesquels les planètes et notre terre elle-même circulent autour du soleil; nous avons en outre par nos observations télescopiques accru le nombre des astres connus d'innombrables étoiles fixes ainsi que de planètesGa naar voetnoot2) nouvelles. Avant le temps de Copernic, et même en partie avant le nôtre, tout ceci gisait enfoui sous de profondes ténèbres. Or, sachant jusqu'à quel point les anciens astronomes ont été dépourvus d'une véritable connaissance du sujet de leurs études, de sorte qu'ils n'ont pu saisir ni la nature des différentes parties du système ni la forme de l'ensemble, l'on comprendra aisément qu'il leur a été impossible d'en construireune bonne image ou représentation artificielle. Quoique dans les écrits des érudits les sphères d'Archimède et de Posidonius - cette dernière étant mentionnée chez CicéronGa naar voetnoot3) - soient beaucoup louées, il est par conséquent certain, malgré ces louanges, qu'elles n'ont pu avoir aucune ressemblance à l'archétype céleste ni aucune conformité de leurs mouvements aux mouvements véritables, bien qu'il soit croyable qu'elles aient été fabriquées avec beaucoup d'intelligence et d'industrie. Nous savons que depuis le temps où l'astronomie fut réformée et rendue plus parfaite, de sorte que l'on pouvait plus facilement entreprendre de pareilles constructions, plusieurs s'y sont en effet appliqués avec succèsGa naar voetnoot4); nous avons vu quelques-unes de leurs productions mécaniques diversement agencéesGa naar voetnoot5). Quant à nous, nous avons fait fabriquer | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 589]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Descriptio automati planetarii.Rerum coelestium scientiam ante bis mille annos inchoatam, magnisque ingeniis excultam, nostra demum aetate absolutam, ut mihi videtur, perfectamque habemus; Idque ita, ut centum circiter his proximis annisGa naar voetnoot1) plus profectum sit quam reliquo omni tempore. Quae enim antea in hac arte pracipua erant, loca stellarum definire tum fixarum tum errantium; anni ac mensium spatia dispescere, Eclipses praedicere, ea omnia non solum multò melius planiusque nunc facere didicimus; sed & quod majus est, ac praeclarius, ordinem, positum, proportionem & figuram orbium caelestium, quibus circa Solem Planetae ac Tellus ipsa circumfertur, summa certitudine comprehensa tenemus; stellas fixas innumeras, planetasque aliosGa naar voetnoot2) Telescopii observationibus perceptos priorum numero addidimus. Quae omnia ante Copernici aevum, quaedam & in nostrum usque, profundis tenebris demersa latebant. Itaque si quis cogitet quantarum in arte sua rerum cognitione veteres Astronomi caruerint; adeo ut nec partes Systematis singulas, nec formam totius habuerint perspectam; facile quoque intelliget fieri non potuisse, ut instar ejus aut imaginem aliquam arte effingerent. Quare etsi plurimùm celebretur doctorum scriptis Archimedea sphaera ac Possidonii illa, cujus apud CiceronemGa naar voetnoot3) mentio facta | reperitur,Ga naar margenoot+ certum tamen est, nullam iis nec archetypi caelestis similitudinem inesse potuisse, nec verorum motuum imitationem, etsi summo ingenio, industriaque fabricatas fuisse credebile sit. Ex eo vero tempore, quo reformata restitutaque in melius fuit Astronomia, sicut facilius res eadem tentari potuit, ita a pluribus quoque susceptam effectamque scimusGa naar voetnoot4); quorum & Machinationes quasdam vidimus, vario artificio elaboratasGa naar voetnoot5). Nos vero ab his omnibus diversam viam secuti tale fabricari curavimus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 590]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
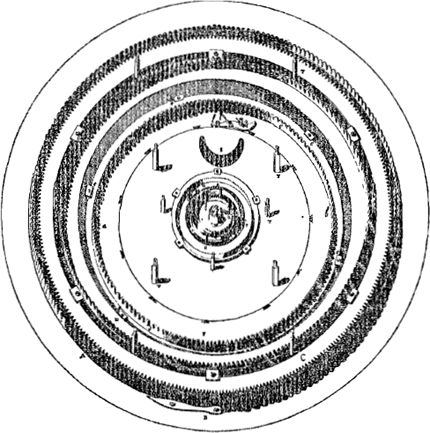
un automate de ce genre d'après un système différent de tous les autres: dans notre planétaire à nous nous avons obtenu par un petit nombre de roues en mouvement continuel que sur la surface d'une table plane les corps des cinq planètes primaires parcourent leurs orbes autour du soleil, et la lune le sien autour de la terre, dans les mêmes périodes qu'au ciel; il s'agit d'orbes excentriques représentant les vraies dimensions et positions des orbes planétaires célestes, tandis que de plus dans chacun d'eux a été conservée l'inégalité du mouvement par laquelle les planètes marchent plus vite lorsqu'elles se trouvent à plus petite distance du soleil. Nous avons noté en outre la petite déclinaison ou angle de leurs plans avec l'écliptique ou plan de l'orbe de la terre. De sorte que, pour ne rien dire de l'élégance du spectacle, la position des planètes peut être trouvée à l'aide de l'automate non seulement pour le présent mais aussi pour le futur ou pour le passé comme par une éphéméride perpétuelle, qu'on y voit donc aussi leurs conjonctions et oppositions tant avec le soleil qu'entre elles, et cela d'autant plus exactement que la machine a été construite à une plus grande échelle. Comme plusieurs ont demandé un exposé de cette invention, voulant ou bien simplement la connaître ou encore l'imiter, nous donnerons dans ce livre la description de l'appareil. Je commencerai par la construction du dehors qui enferme tout le mécanisme. Cette partie extérieure a la forme d'un octogone lequel est de bois et possède un diamètre de deux pieds et une épaisseur de six pouces. La boîte est suspendue au mur et balancée sur ses gonds - lesquels se trouvent à gauche - de sorte qu'on peut la tourner quand on veut et l'ouvrir par derrière pour examiner l'intérieur. Par devant on voit une table de cuivre doré recouvrant tout l'espace octogone et protégée par une glace, sur laquelle table sont tracés les orbes des planètes d'après le système de Copernic mais suivant les proportions keplériennes. Ces orbes sont découpés de telle manière et si profondément que par les fentes se peuvent mouvoir de petites pinnules entraînant les planètes en forme de demi-globes lesquels cheminent au dessus de la table et glissent pour ainsi dire sur sa surface; dans ce mouvement Saturne porte avec lui cinq satellites, Jupiter quatre, et la Terre un seul qui est notre Lune, ceux-ci étant placés sur les mêmes ronds que les petits corps des planètes. Il faut savoir qu'aux autres planètes qui ne possèdent pas de satellites j'ai néanmoins attaché des ronds de même espèce pouvant représenter l'éther environnantGa naar voetnoot6) et rendant en même temps les planètes [Fig. 140] mieux visibles. Toutes les planètes primaires, savoir, outre celles déjà nommées, Mars, Vénus et Mercure décrivent d'une façon continue leurs mouvements autour du Soleil immobile en observant exactement non seulement leurs | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 591]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Automaton, in quo exiguo rotarum continenter euntium numero effecimus, ut in tabulae planae superficie Planetarum quinque primariorum corpora circa Solem, Lunae vero circa Terram, cursus suos absolverent, iisdem quibus in caelo temporibus, atque in iis orbibus excentricis, qui caelestium veram dimensionem positumque exprimerent; servata quoque in singulis motuum inaequalitate, qua celerius feruntur in partibus a Sole minus remotis: & annotata denique exigua illa declinatione qua ab Eclipticae sive orbitae Telluris plano evagantur. Adeo ut praeter spectaculi elegantiam, etiam positus Planetarum non modo in praesens tempus sed & in futurum aut praeteritum, tanquam ex perpetua quadam ephemeride hinc discere liceat, nec non conjunctiones, oppositionesque omnium, cum ad solem, tum inter se; idque tanto exactius, quanto ampliore forma opus effectum fuerit. Quae inventio cum a multis expetita sit, qui vel cognoscete vel imitari eam cuperent, hoc libro cujusmodi sit exponemus. Incipiam vero a Machinae constructione exteriori, quae totum opus complectitur. Itaque Octogonum est è ligno coagmentatum, bipedali diametro, profunditate pollicum sex. Hoc ad parietem ita suspensum est, & cardinibus suis libratum,| qui inGa naar margenoot+ sinistro latere affixi sunt, ut cum libuerit converti machina possit, & aversa parte recludi, quo interiora conspiciantur. Facie anteriori lamina ex aere aurata cernitur toti octogono praetensa ac vitro speculari tecta, in qua Planetarum orbes secundum Copernici systema, sed Keplerianas proportiones descripti sunt, ac penitus excisi, adeo ut per rimas eas pinnulae exiguae commeent, quibus Planetarum globuli dimidiati supra laminam ac velut in superficie ejus volvantur, Saturno quinos, Jove quaternos, Tellure unicum comitem, quae Luna nostra est, secum ferente, qui nimirum comites iisdem orbiculis impositi sunt, quibus Planetarum ipsorum corpuscula. Nam & caeteris planetis qui comites nullos habent, ejusmodi tamen orbiculos addidi, qui circumfusum aetheraGa naar voetnoot6) referrent, simulque planetas efficerent visibiliores. Ac Planetae quidem primarii omnes, ut sunt praeter jam dictos, Mars, Venus, Mercurius, ita continue motus suos circa Solem immobilem peragunt, ut non tantum periodica tempora, sed & ano- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 592]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
temps périodiques mais aussi les lois de l'anomalieGa naar voetnoot7). La Lune, elle, fait des révolutions mensuelles autour de la Terre. Mais il n'a pas été possible de faire accomplir des révolutions aux Satellites de Saturne et de Jupiter, tant à cause de la petitesse de la machine que pour ne pas accroître le travail outre mesure. Ces satellites-là ne sont donc attachés qu'à un seul disque dont la planète primaire occupe le centre. 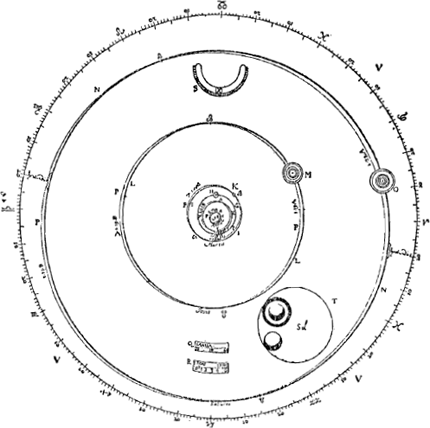 [Fig. 140]
La circonférence de cercle qui représente l'écliptique embrasse tous les orbes planétaires; elle est divisée en ses douze signes et 360 degrés. Toutes les positions apparentes des astres considérés par rapport à l'écliptique sont facilement déterminées | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 593]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
maliae leges exacte serventGa naar voetnoot7). Circa Terram vero Luna menstruas revolutiones conficit. At in Saturni Jovisque comitibus idem perficere non licuit; cum ob machinae parvitatem, tum ne aequo longius labor excresceret. Itaque hi uno tantum orbiculo affixi tenentur, cujus primarius Planeta centrum occupat. Porro omnes Orbitas Planetarias Eclipticae circulus amplectitur, signis suis duodecim, gradibusque 360 divisus. In quo apparentia horum astrorum loca, facillime sic investigantur. Nempe si locum Planetae secundum longitudinem, ut vocant, inquirere | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 594]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
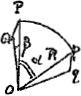
comme suit: pour trouver le lieu d'une planète d'après sa longitude, comme on dit, il suffit de tendre un fil de la terre à la planète, auquel fil un autre partant du centre fixe du soleil est tendu parallèlement jusqu'à une certaine division de l'écliptique laquelle indiquera la longitude cherchée. Or, cette opération peut également être exécutée, sans ouvrir la glace dont nous avons parlé plus haut, à l'aide d'un certain
 [Fig. 141]
parallélogramme composé de deux bâtonnets égaux et de deux fils pareillement égaux entr'eux qui y sont attachés: on place ce parallélogramme sur la glace et, en laissant l'oeil dans la même position, on l'y adapte de telle manière que tandis que l'un des deux fils passe par les centres de la terre et de la planète, l'autre est dirigé suivant un rayon du soleil, auquel cas ce dernier fil indiquera sur l'écliptique le lieu de la planète suivant sa longitude. Quant à la détermination de sa latitude nous en parlerons plus loin lorsque nous aurons fait connaître quelles circonférences de cercle il a fallu tracer à cet effet. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 595]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
placet, tantummodo filum è Tellure ad planetam illum extenditur; eique filo alterum ex Solis centro, quod ibi fi|xum manet, Parallelum ducitur ad Eclipticae divisionesGa naar margenoot+ usque; hoc enim Planetae longitudinem ostendet. Atque idem hoc parallelogrammo quodam filari ex bacillis duobus aequalibus duo fila itidem aequalia innexa habentibus constante peragi potest, clauso manente vitreo, quod supra indicavimus, operculo. Huic enim parallelogrammum imponitur, atque oculo desuper manente immoto, ita coaptatur, ut altero filo super Terrae ac Planetae centrum transeunte, alterum Soli immineat, quod simul in Eclipticae circulo locum Planetae secundum longitudinem indicabit; de latitudine vero cognoscenda postea dicemus, postquam circulos in hunc usum describere docuerimus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 596]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
À la partie inférieure de la table, entre les orbes de Saturne et de Jupiter, il y a deux ouvertures peu distantes l'une de l'autre, longues de deux pouces, larges d'un demi-pouce, où paraissent, dans la plus haute le jour du mois, dans l'autre l'an de notre ère. Comme tout le reste, ces chiffres correspondent à des rouages particuliers lesquels tournent par le mouvement de l'automate, la première roue ayant des divisions égales de 3 × 365 joursGa naar voetnoot8), et la deuxième de trois cents ans (voyez la Fig. 141). Le mouvement susdit provient d'une horloge intérieure qui indique de plus les heures et les minutes dans une ouverture sémicirculaire faite à la partie supérieure entre les orbes de Jupiter et de Mars. En effet, tandis que le numéro de chaque heure y passe, elle en fait voir en même temps les parties sexagésimales. Mais toute la machine peut aussi être mise en mouvement à la main soit qu'on veuille, pour jouir de ce spectacle, faire parcourir aux planètes leurs orbes en peu de temps, soit aussi qu'il faille connaître leurs positions à un moment donné passé ou futur. Dans ce but on applique à la partie droite de l'octogone une manivelle qui, tournée sans effort, ajoute par chaque révolution le mouvement d'une année à la position de toutes les planètes, ou bien, lorsqu'on tourne en sens contraire, les fait rétrograder d'autant, de sorte que la position de ces corps célestes peut être représentée telle qu'elle a été dans les derniers cent ans ou bien telle qu'elle sera dans le cours des deux siècles qui suivront. On ramène ensuite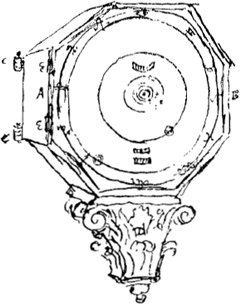 [Fig. 142]
le tout au temps présent avec la même facilité, tournant la manivelle jusqu'à ce que le jour et l'an réapparaissent au milieu des dites ouvertures. Ceci étant accompli, il faut enlever la manivelle pour que tout le mécanisme reprenne le mouvement automatique qu'il avait auparavant. Pour qu'on saisisse d'autant mieux ce qui a été exposé jusqu'ici nous intercalons la figure de l'automate [Fig. 142]Ga naar voetnoot9) tel qu'il apparaît à l'extérieur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 597]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Inferiori parte Laminae, inter Saturni Jovisque orbitas foramina bina sunt parvo intervallo distantia, binosque pollices longa, dimidium lata, quorum superiore dies Mensis, altero Annus Epochae nostrae comparet, itidem ut caetera suis orbibus delati & Automati motu volubiles, quorum ille ter 365 dierum aequales divisiones habetGa naar voetnoot8), hic trecentorum annorum. Motus autem ab incluso horologio oritur, quod idem horas quoque & scrupula prima indicat in semicirculari foramine inter Jovis ac Martis Orbes parte superiori inciso. In eo namque numerus horae cujusque ordine praeterlabens, particulas quoque sexagesimas una opera demonstrat. Movetur autem & manu machina tota, cum vel spectaculi gratia Planetarum discursus exigui temporis mora transigi placet, vel ad tempus datum futurum praeteritumve positus eorum requiritur. Tunc enim lateri dextro Octogoni manubrium inseritur, quod levi manus motu conversum, qualibet circumductione annuum motum planetis universis superaddit; vel con | traria ratione agitatum tantundem illos in praecedentiaGa naar margenoot+ retrahit, ut retrorsum quidem in centenos annos, in futurum ad ducenos, quaecunque fuit aut futura est coeli positura repraesentari queat. Pari vero facilitate omnia rursus ad praesens tempus reducuntur, converso manubrio, donec ad puncta dictorum foraminum media dies annusque restituantur. Quo peracto auferendum est manubrium, ut rursus automatico motu omnia sicuti prius ferantur. Sed quae hactenus exposita sunt, quo clarius percipiantur figuram hanc Automati, quale extrinsecus apparet, adjicimusGa naar voetnoot9). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 598]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 140]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explication de la fig. 140.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 599]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explanatio Tab. 1. Fig. 1.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 600]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
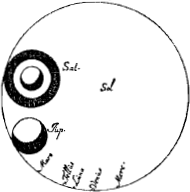 [Fig. 143]
La figure 143 montre la vraie proportion de la dimension du disque solaire à ceux de toutes les autres [sic] planètes. Il faut savoir, qu'il était impossible que dans la machine les corps du soleil et des planètes fussent représentés suivant les véritables proportions de leurs dimensions à celles des orbites: il auraient tous été invisibles à cause de leur petitesse. C'est pourquoi nous les avons tous fait graver à part en un endroit vacant de la table en indiquant les dimensions de chacun d'eux. Le plus grand cercle y représente le soleil, les autres les planètes placées contre le bord intérieur du soleil pour que les véritables rapports de leurs grandeurs tant entre elles qu'à l'égard de lui apparaissent distinctement. Ces rapports ont été calculés en tenant compte tant de la comparaison des distances que de celle des grandeurs des diamètres tels qu'on les observe avec le télescope, comme cela est expliqué dans ce que nous avons écrit jadis sur les merveilleuses formes de SaturneGa naar voetnoot10). Or, ces corps planétaires sont bien plus petits par rapport à la grandeur du soleil que ne l'ont enseigné les astronomes antérieurs. Il n'est pas étonnant que parmi eux les anciens, déjà mentionnés plus haut, qui ne connaissaient pas les rapports des orbes entre eux et qui d'autre part mesuraient les diamètres des planètes à l'oeil nu et sans grande application, se soient égarés de beaucoup; mais les astronomes plus récents, même ceux qui ont écrit après l'invention du télescope, ont encore publié des mesures bien différentes des nôtres. Je n'hésite pas à affirmer que ces dernières sont plus exactes puisque nous avons en premier lieu observé ces astres avec de plus grands télescopes et que d'autre part nous avons mesuré | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 601]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fig. 2.Fig. 2. Exhibet veram proportionem magnitudinis disci Solaris, ad reliquorum omnium Planetarum discos.
Caeterum fieri non poterat, ut ipsa Solis & Planetarum corpora suis proportionibus ad hunc orbitarum modulum exprimerentur; quippe quae omnia visu percipi ob exilitatem nequirent:Ga naar voetnoot*) idcirco seorsim eos omnes in tabulae loco vacuo describendos curavimus ea, quae hic signata est, magnitudine. Itaque major circulus Solem refert, reliqui Planetas juxta Solem positos ut vera eorum tum inter se tum ad Solem magnitudinis ratio appareat. Ea vero & ex distantiarum & ex diametrorum telescopio observatorum comparatione constituta est; quemadmodum in his, quae de Saturni mirabilibus formis olim conscripsimus,Ga naar voetnoot10) est explicatum. Sunt quidem haec Planetarum corpuscula ad Solis magnitudinem multo exiliora, quam ab astronomis qui ante nos suere sunt prodita. E quibus prisci illi qui nec orbium inter se rationem cognitam habebant, & nudo visu atque indiligenter prorsus Planetarum diametros metiebantur, non mirum est si longissime aberrarunt; recentiores vero, quique invento jam telescopio scripsere, etiam hi non parum ab hisce mensuris nostris diversi abierunt. Quas equidem veriores esse adseverare non vereor, quod & ma|joribus organis visoriis haec sidera nos observavimusGa naar margenoot+ & certiori ratione diametros dimensi simus. Itaque quae Solem inter caeterosque Pla- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 602]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
leurs diamètres d'après une méthode plus sûre. Le rapport qu'on voit indiqué ici entre le soleil et les autres planètes est donc certain, ou du moins il ne diffère du rapport véritable ou point du tout ou fort peuGa naar voetnoot11). Seul le rapport de la grandeur de la terre à celle du soleil a été établi avec moins de certitude: nous l'avons défini en disant que, puisque la terre est placée entre les astres Mars et Vénus, on peut aussi par hypothèse adopter pour sa grandeur une valeur intermédiaireGa naar voetnoot12). Ce raisonnement conduit à une distance du soleil d'environ 12000 diamètres terrestres et à une valeur 1:110Ga naar voetnoot13) pour le rapport du diamètre terrestre à celui du soleil; or, ces valeurs ont été très bien confirmées par la fort subtile observation de certaines parallaxes postérieurement exécutée par d'excellents astronomes, observation qui leur a permis de calculer la distance de Vénus en son périgéeGa naar voetnoot14). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 603]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
netas hic cernitur expressa ratio, ea certa est, atque a vera vel nihil vel minimum quid diversa.Ga naar voetnoot11) Una tantum Telluris minus liquido comperta est, quam nos hac ratione definivimus; ut sicut loco inter Martis & Veneris stellas media est Tellus, ita ponatur & magnitudineGa naar voetnoot12); exinde distantia Solis circiter 12000 Terrae diametrorum efficitur, Terraeque diameter ad Solarem ut 1 ad 110Ga naar voetnoot13); quas tamen mensuras subtillissima illa parallaxium observatio a summis astronomis postea adhibita, qua Veneris perigaei distantiam ad calculos revocarunt, egregie confirmavitGa naar voetnoot14). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 604]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
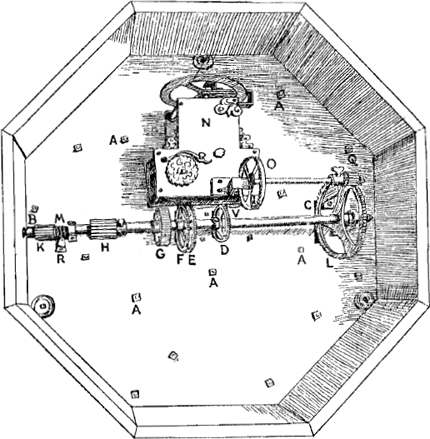
Quant au mouvement apercevable au dedans de l'automate [Fig. 144], son agencement est reconnu en considérant attentivement l'intérieur après avoir tourné la boîte. En effet, après avoir enlevé la planche qui recouvre la machine de ce côté, on voit apparaître dans son corps une table de cuivre occupant, comme celle de devant,
 [Fig. 144]
tout l'octogone; elle est distante d'un pouce de cette dernière et porte plusieurs petites colonnes. En second lieu un axe transversal de fer se présente à la vue long de deux pieds et pourvu d'un nombre de roues égal à celui des planètes, chaque roue y étant attachée avec une vis passant par le moyeu. Les dents de ces roues s'adaptent à celles d'autres roues plus grandes faisant circuler les différentes planètes et situées entre les deux tables ou plaques. Il y a en outre sur le même axe commun encore une autre roue destinée à faire tourner le cercle des jours et des mois, ainsi qu'une particule d'une vis sans fin, comme on a l'habitude de dire, laquelle par l'intermédiaire d'un | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 605]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Motus autem, qui in hoc Automato cernitur, ratio converso pegmate, inspectaque intus machina cognoscitur. Reducto enim quod hac parte eam claudit operculo, apparet intus lamina ex aere octogonum totum, uti anterior, occupans, atque ab illa anteriore pollicis unius intervallo remota, & columellis pluribus conserta. Porro axis quidam ferreus hic apparet bipedalis transversim objectus, ac totidem, quot sunt Planetae, rotis instructus, quarum unaquaeque cochlea una per modiolum trajecta affigitur. Harum rotarum dentes dentibus majorum rotarum Planetas singulos circumferentium, interque binas laminas jacentium aptantur. Porro eidem axi communi alia praeterea rota insidet circulo dierum ac mensium convertendo destinata; itemque cochleae, quam | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 606]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
certain petit axe denté, fait tourner, une fois en trois cents ans, un cercle où se trouvent inscrits les chiffres correspondants à chacun d'eux. Or, la position de cet axe de fer est la suivante: il est horizontal mais non pas parallèle à la grande table dont nous avons parlé: à droite, pour celui qui examine l'intérieur de l'automate, il s'en écarte beaucoup plus que de l'autre côté, ce qui a dû être fait ainsi pour que la conversion de cet axe unique pût suffire pour mettre en mouvement toutes les planètes. Les nombres des dents ont été trouvés d'après une méthode que nous expliquerons un peu plus loin; ils sont adaptés si exactement aux mouvements moyens qu'en vingt ans il suffit de faire avancer Saturne de 1 minute 34 secondes, Jupiter de 1′ 9″, Mars de 24′ 0″, Vénus de 3o 37′, Mercure de 7′ 47″, la Lune de 1o 31′Ga naar voetnoot15). Nous n'avons d'ailleurs pas seulement représenté les mouvements moyens, mais outre ceux-ci l'inégalité qui existe en réalité dans la marche de chacune des planètes, ceci suivant les anomalies établies par Kepler dont l'autorité est fort grande auprès des astronomesGa naar voetnoot16). Nous ferons voir en lieu propre comment cette inégalité est obtenue. On voit en outre de ce côté du planétaire l'horloge automatique attachée à la dite table un peu au dessus de l'axe, par la force de laquelle ce grand axe exécute ses révolutions annuelles entretenant le mouvement continu universel; en effet, le mouvement est transmis par l'horloge à la roue montée sur l'axe que nous avons dite être adaptée au cercle des jours et des mois, comme cela paraîtra plus clairement dans la figure ci-jointe [Fig. 144]. Il serait inutile de décrire l'intérieur de l'horloge, puisque cette invention est bien connue. Elle est mise en mouvement par un ressort spiral. Or, nous avons ici assuré l'uniformité du mouvement par un deuxième ressort hélicoïdal capable de tempérer les oscillations par sa vertu égalisatrice, remède que nous avons conçu en second lieu après l'invention du penduleGa naar voetnoot17); il est en vérité moins sûr que celui-ci, puisque la force du ressort augmente ou diminue quelque peu par le froid et la chaleur; mais ici cet agencement était plus apte et plus pratique. Quant au premier ressort, il doit être remonté une fois par semaine. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 607]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
infinitam vocant, particula, quae circulum cum inscriptis annis trecentis, totidem annorum spatio semel circumducit, intercedente axiculo quodam dentato. Positum vero axis ferrei quod attinet, is horizonti quidem parallelus est, non autem laminae magnae quam|jam demonstravimus, sed parte ea, quae inspicienti dextra est,Ga naar margenoot+ multo magis ab illa recedit, quod ita faciendum fuit, ut commodius unius axis conversio omnium planetarum diversis motibus sufficeret. Dentium vero numeri certa ratione, quam mox exponemus, reperti sunt, tamque exacte mediis motibus aptati, ut in annis viginti Saturnus tantum scrupulo 1, 34″ promovendus sit, Jupiter 1′, 9″. Mars 24′, 0″. Venus gradibus 3. scrup. 37′, Mercurius 7′, 47″. Luna parte 1, scrup. 31′Ga naar voetnoot15). Caeterum non tantum motus medios exhibuimus, sed & cum inaequalitate ea quae reipsa planetarum cursibus inest; idque secundum anomalias a Keplero excogitatas, quarum apud astronomos maxima auctoritasGa naar voetnoot16). Quo pacto autem haec inaequalitas conficiatur suo loco ostendemus. Porro etiam horologium Automaton hac parte conspicitur paulo supra axem dictae laminae adfixum, cujus horologii vi axis ille magnus annuas conversiones facit, ac per eum omnia continuo motu cientur; transit enim motus ab horologio in rotam axi infixam quam dierum ac mensium circulo aptari diximus, quemadmodum in adscripto typo apertius liquebit. Interiora horologii percensere nihil necesse est, cum vulgo notum sit inventum, cujus nimirum vis a lamina in helicem convoluta. Hic vero motus aequalitatem alia ἑλιϰώδεϊ lamina adjuvimus, quae libramento recursus temperaretGa naar voetnoot17); quod alterum post inventa pendula remedium excogitavimus non aeque tutum quidem, quod frigore & calore elater vires suas paulatim quid intendat ac remittat, sed hîc aptius convenientiusque. Intenditur autem lamina ilia prior motus effectrix septenis quibusque diebus.| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 608]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 144].
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explication de la Fig. 144.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 609]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ExplanatioGa naar margenoot+ Tab. 2. Fig. 3.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 610]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
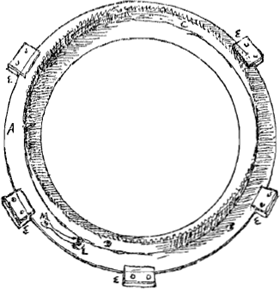
 [Fig. 144 bis]
Dans la Fig. 144 qui représente l'aspect de la machine retournée après l'enlèvement de la planche qui la recouvrait, les plaques carrées indiquées par la lettre A et les autres qui leur sont semblables, tiennent pas des vis les extrémités des colonnes qui rattachent à la table qu'on voit de ce côté l'autre table mentionnée plus haut, celle de devant, qui est coupée en parties par les orbes des planètes. L'axe de fer long de deux pieds est CB, lequel est distant de la table de deux pouces du côté où se trouve la lettre C. Les roues montées sur cet axe font circuler les planètes dans leurs orbes, D étant la roue de Mercure, E celle de Vénus, F celle de la Terre, G celle de Mars, H celle de Jupiter, K celle de Saturne. Quant au cercle sur lequel sont inscrits les mois et les jours, c'est la roue L qui le meut; et la révolution en 300 ans est effectuée par celle de la vis sans fin M par l'intermédiaire de deux pignons attachés à un même axicule et possédant chacun 6 dents, dont l'une engrène dans cette vis et l'autre, intérieurement, dans les dents de la grande roue des 300 ans. C'est donc par les révolutions annuelles du seul axe CB (car la roue L et la vis M en font aussi partie) qu'une si grande diversité de mouvements est produite. Or, cet axe est mis en mouvement par l'horloge de la manière suivante. Il y a dans elle une roue V, partiellement visible dans la figure, qui fait ses révolutions en 96 heures. À l'autre extrémité de l'axe de cette roue, en PGa naar voetnoot18), ont été entaillées quatre dents lesquelles engrènent dans une roue O à 45 dents. L'axe de cette dernière porte également un tympan Q à neuf dents qui engrènent dans les 73 dents de la roue L. Il faut maintenant figurer les roues planétaires situées entre les deux tables pour qu'il apparaisse comment elles sont construites et quel est leur mouvement. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 611]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In schemate adscripto, quae conversae machinae faciem amoto operculo exhibet,Ga naar margenoot+ lamellae quadratae, quibus adscriptum est a, reliquaeque iis similes, eae columellarum capita cochleis adstringunt, quibus columellis laminae, quae hic cernitur, connectitur anterior illa Planetarum orbibus in partes dissecta. Axis bipedalis ferreus est cb, parte ea, qua c adscriptum est, pollices binos a lamina distans. In hoc axe defixae rotae orbes planetarum circumagunt, d quidem Mercurii, e Veneris, f Telluris, g Martis, h Jovis, k Saturni. Circulum vero cui menses diesque inscripti sunt rota l movet, ac denique annorum 300 circuitum efficit cochleae m convolutio, intercedentibus rotulis binis communi axiculo affixis, quibus singulis dentes 6, quarumque altera cochleae huic convenit, altera interior rotae annorum magnae dentibus inseritur. Per unum igitur axem cb annuas conversiones peragentem, (namque & rota l & cochlea m ipsi inhaerent) tot motuum diversitas perficitur; axis autem ab horologio hoc modo cietur. Est in horologio rota v, cujus hic particula tantum cernitur horis 96. singulas conversiones faciens. Hujus axi altero capite ad pGa naar voetnoot18) dentes additi sunt quaterni, hi inseruntur rotae o dentibus 45. cui rotae in communi axi jungitur tympanum q. novem dentibus incisum; qui denique aptantur dentibus 73 rotae l. Oportet nunc & interjectas utrique laminae planetarum rotas inspiciundas dare, ut quomodo constructae sint & quo pacto circumeant, appareat. | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 612]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 141.]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explication de la Fig. 141.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 613]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ExplanatioGa naar margenoot+ Tab. 3. Fig. 4.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 614]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 141 bis]
placé sur un petit axe attaché à l'anneau, de telle manière que le globule se trouve, à l'extérieur, à une petite distance de la dite table antérieure. Auprès des circonférences extérieures de ces anneaux sont placées certaines roulettes attachées à la table lesquelles guident les rotations des anneaux et les empêchent en même temps de s'écarter d'elle. Il y en a cinq ou six pour les planètes supérieures Saturne et Jupiter, vu la grandeur des anneaux qui leur correspondent, pour les autres quatre ou trois suffisent. Dans la Fig. 141 l'anneau plan est ab [ou AB dans la Fig. 141 bis | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 615]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Singulis igitur Planetis annulus planus ad orbitae eorum amplitudinem dicatus est, cui armilla dentata rectis angulis insistit, aequaliter undique ab annuli peripheria distansGa naar voetnoot19). Annulus iste Tabulae octogonae anteriori intus applicitus globulum, Planetae corpus referentem, circumfert, stylo exiguo sibi infixum, quo extra laminam anteriorem tantillo promineat. In circumferentia annuli hujus repagula quaedam collocata sunt laminaeque adfixa intra quae circulari motu ipsi moventur, simulque ut ne a jam dicta lamina recedant continentur. Horum in Planetis superioribus Saturno ac Jove quina aut sena adjecta sunt propter annulorum magnitudinem, in reliquis quaterna aut trina sufficiunt. In figura hic descripta annulus planus est ab, super hunc erecta armilla ac dentibus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 616]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
omise par les éditeurs]; la couronne dentée dressée sur lui est cd [ou CD]. Les roulettes guidant l'anneau plan à l'extérieur sont désignées par ee [ou EE]. Elles se composent chacune de deux parties, savoir d'une partie inférieure que frise la circonference extérieure de l'anneau et qui est attachée à part à la table planétaire, et d'une partie supérieure jointe à l'autre par des vis laquelle recouvre tant soit peu le contour de l'anneau et l'empêche ainsi de sortir de son plan comme on peut le voir dans la figure. C'est donc par de tels anneaux que sont charriées les diverses planètes, parcourant ainsi des orbites circulaires. Si nous avions voulu faire celles-ci elliptiques, ceci aussi aurait été d'une exécution facile, puisque chaque planète n'est pas attachée à l'anneau ab lui-même, mais à la petite lame lm mobile autour de l'axicule M et attachée, elle, à l'anneau, laquelle porte en L la planète insérée dans un tube; en cet endroit il faudrait faire dans l'anneau un trou un peu plus grand, de cette façon la planète pourrait aisément se mouvoir dans une fente elliptique. Toutefois, comme ces ellipses ne diffèrent que fort peu de circonférences de cercles, il ne nous a pas semblé y avoir une raison suffisante pour les introduire. Mais pour les planètes Saturne et Jupiter nous avons effectué par la dite méthode qu'elles se meuvent un peu plus librement par leurs fentes assez étroites. Tout semblable à ces anneaux est celui sur lequel sont inscrites es divisions des jours; mais le cercle des ans n'a que l'anneau plan seulement pourvu de dents à l'extérieur; nous avons dit plus haut comment il est mis en mouvement. Pour ces anneaux des jours et des ans nous avons trouvé une place entre ceux qui portent Saturne et Jupiter; par conséquent dans la table antérieure les ouvertures par lesquelles on voit ces divisions ont été pratiquées entre les orbites de ces deux planètes. 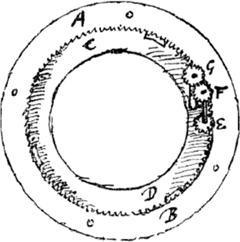 [Fig. 145]
Il faut maintenant faire voir comment le mouvement mensuel de la Lune est obtenu. Qu'on considère la partie de la table antérieure qui est bornée par les orbites de Mars et de la Terre. À cette partie est attaché, par derrière, un anneau portant 137 dents à sa circonférence intérieure; dans la Fig. 145 il est indiqué par les lettres inscrites A B. Cette circonférence dentée est un peu plus grande que l'orbite annuelle de la Terre, et l'anneau AB s'élève un peu au-dessus du plan auquel il est attaché, de sorte que peuvent être placées sous lui les roulettes entre lesquelles tourne l'anneau qui porte la Terre, lequel est indiqué par les lettres C D. L'anneau CD fait tourner avec lui un axicule qu'il porte et qui lui est perpendiculaire, aux extrémités duquel sont attachés les pignons E, F, dont l'inférieure a douze dents | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 617]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
incisa cd. Repagula annulum planum in ambitu continentia ee. Haec singula duabus partibus constant, inferiore quam extrema annuli circumferentia radit, quaeque seorsim laminae Planetariae adfixa est; tum alia huic superposita & cochleis conjuncta, quae paulum supra annuli marginem protenditur, atque ut ne excidere possit impedit, sicut in figura videre est.| Hujusmodi itaque annulis singuli Planetae feruntur, ac circulares orbitas percurrunt.Ga naar margenoot+ Quod si Ellipticas voluissemus, nullo negotio id quoque efficere licebat, defixo scilicet Planeta non in annulum ipsum ab, sed in brachiolum lm, ipsi inhaerens, quod movetur in axiculo m; in l vero Planetam tubulo insertum gerat; qua parte annulus laxiori foramine perforandus. Sic enim facile per rimam Ellipticam planeta ducetur. Sed cum parum adeo a circulis Ellipses istae differant, non satis caussae visum, ut eas adhiberemus. In Saturno autem ac Jove, quo liberius per rimas angustiores circuli laberentur hac ipsâ ratione effecimus. Est autem his prorsus similis ille, cui dierum divisiones inscriptae sunt; ut annorum circulus solum annulum planum habet dentibus in circumferentia incisis, qui quomodo motum accipiat jam ante dictum. Et his quidem dierum & annorum annulis locus repertus est inter illos qui Saturni & Jovis Planetas vehunt; Eoque & foramina, quibus divisiones illae spectentur, inter istorum orbitas Planetarum in anteriore tabula sunt incisa. Jam de menstruo Lunae motu ostendendum qua ratione ordinatus sit. Inter Martis ac Terrae orbitas quod interjacet laminae Planetariae segmentum, in eo intus defixus est annulus, interiore cirumferentia dentes habens 137, quem in hoc schemate significant inscriptae literae ab. Circumferentia haec dentata paulo major est orbita terrae annuâ, atque ipse annulus ab paulum supra planum, cui affixus est, attollitur, ut sub ipso collocari queant repagula, intra quae volvitur annulus Tellurem ferens, qui notatus est literis cd. Hic porro annulus axiculum circumfert ad rectos angulos sibi insistentem, rotulasque utroque capite affixas habentem e, f, quarum inferior duodenos dentes | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 618]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
engrenant dans celles de l'anneau AB, tandis que le pignon supérieur en a treize. Ces dernières engrènent dans les 12 dents du pignon G juxtaposé ayant lui aussi son axe planté dans l'anneau CD; or, cet axe a une cavité regardant la face antérieure de la table planétaire, dans laquelle cavité est fixée un petit axe attaché au cercle lunaire. Pour que rien n'empêche la vue des deux pignons E, F, je n'ai cru devoir représenter dans la figure ni un certain rétinacle attaché à l'anneau CD lequel tient en place, par
 [Fig. 140]
leurs extrémités supérieures, les deux petits axes mentionnés, ni aussi la couronne dentée. Lorsque l'anneau terrestre CD tourne suivant l'ordre des lettres A E B, révolution qui vue sur la face de devant de la table procède suivant l'ordre des signes du zodiaque, il est nécessaire que les pignons E et F tournent à rebours, et le pignon G de nouveau dans le sens opposé à celui de E et F, donc dans le même sens que l'anneau de la Terre. Or, nous avons dit qu'un petit axe est inséré dans l'axe cave du pignon G, auquel axe est attaché le petit anneau qui porte la Lune sur son bord et la Terre en | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 619]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
habet commissos dentibus | annuli ab, superior tredecim. Superioris dentes inserunturGa naar margenoot+ dentibus 12 rotulae g juxta collocatae, axemque itidem annulo cd infixum habenti, qui quidem axis cavitatem habet in partem anteriorem tabulae Planetariae patentem, in quam cavitatem defigitur stylus exiguus ac lunari circello conjunctus. Caeterum nec retinaculum quoddam annulo cd affixum & utrosque, quos diximus, axiculos parte superiori detinens, uti nec armillam dentatam exprimendam duxi, ne quid rotularum ef conspectum impediret. Revoluto itaque annulo Terrestri cd secundum ordinem literarum aeb, quae revolutio anteriori tabulae parte spectata incedit secundum signorum ordinem zodiaci; necesse est contrario motu circumire rotulas e & f, atque huic rursus contrario rotulam g, hoc est, in partem eandem cum annulo Telluris: diximus autem in axem cavum rotulae g stylum inseri, cui cohaeret orbiculus Lunam in circumferentia gerens, Tellu- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 620]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
son centre, d'où résulte que le parcours de la Lune est bien ordonné; il paraîtra plus loin jusqu'à quel point il s'accorde avec la période du mois.
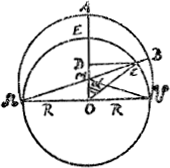
Ayant exposé jusqu'ici les différentes parties de la machine, nous dirons maintenant avec quelles proportions des rayons et de quels centres nous avons décrit les orbites des planètes sur la table antérieure et aussi où nous avons placé les points des aphélies et des noeuds; ensuite quel nombre de dents nous avons attribué à chaque roue pour obtenir les bons rapports des mouvements moyens et par quelle méthode nous avons calculé ces nombres; enfin par quelle construction des dents nous avons réussi à représenter les anomalies telles qu'elles doivent être. Voici ce que nous avons fait. Après avoir décidé que la grandeur de la table octogone serait telle que la perpendiculaire du centre sur un quelconque des côtés aurait la longueur de 11½ pouces, nous avons décrit avec un rayon de 10½ pouces du même centre, où il faut mettre le Soleil, la circonférence de cercle des signes de l'écliptique. [Fig. 140]. Nous avons divisé cette circonférence en 360 parties et nous avons mis les 12 signes chacun en son lieu, plaçant celui du Bélier à droite à la hauteur du centre. Les lieux des aphélies marqués dans un tableau joint à l'écliptique font voir dans quelles directions les centres des orbites ont été pris pour chaque planète. Et les valeurs des rapports des rayons compris dans le même tableau font connaître aussi la grandeur de chacun d'eux aussitôt que la longueur d'un d'eux, ici le rayon de l'orbe terrestre, est donné. Or, nous a vons donné à ce dernier rayon la longueur d'un pouce, c.à.d. celle de la douzième partie du pied rhénan. En prenant le rayon de l'orbite de la Terre de 100000 parties, les autres rayons auront les nombres de parties marqués dans le tableau. Les excentricités ici notées sont aussi exprimées dans la même unité. Il faut les considérer comme portées du centre de l'écliptique, où est le lieu du Soleil, vers les lieux des aphélies: leurs extrémités désignent alors le centre de chaque orbite. Voulant p.e. décrire la route de Saturne au commencement de l'année de Christ 1682, je tire une droite du centre de l'ellipse au point 27o40′ du Sagittaire, je porte sur elle à partir du même centre 54 parties telles que le rayon de la terre, c.a.d. un pouce, en contient 100: on ne peut pas, à cette petite échelle, prendre plus de décimales. Je trouve ainsi le centre de l'orbite de Saturne. Alors, prenant un rayon de 951 des mêmes parties, je décris l'orbite de la planète et je marque de la lettre A son aphélie là où l'orbite est coupée par la droite que j'ai dit être tirée du centre. Mais comme dans le ciel toutes les orbites planétaires font un certain angle avec l'écliptique ou plan de l'orbite terrestre, ce dernier étant ici censé coïncider avec la surface de la table, de telle manière évidemment que chaque plan est moitié au dessus, moitié au dessous de l'écliptique, il est clair que ce ne sont pas les orbites des planètes elles-mêmes que nous avons décrites mais leurs projections orthogonales sur le plan de l'écliptique, projections que nous considérons cependant comme étant elles-mêmes les orbites, vu que c'est d'après elles qu'on examine le mouvement longitudinal de la planète, quoique ce ne soient en vérité que les orbites rapportées au plan de l'écliptique. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 621]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
rem vero in centro; quare recte ordinatus est Lunae circuitus; quam bene vero tempori Mensis Periodici conveniat inferius manifestum fiet. Expositis hactenus singulis machinae partibus, dicemus jam, quibus semidiametrorum inter se proportionibus, quibusque centris orbitas Planetarum in Tabula anteriore descripserimus, item ubi Apheliorum ac Nodorum puncta constituerimus; deinde quem dentium numerum rotae cuique tribuerimus, ut mediorum motuum constaret ratio, deque ejusmodi numerorum inventione; ac denique qua dentium constructione debitas motuum anomalias expediverimus. Igitur octogonae laminae statuta hac magnitudine, ut quae ex centro in latus perpendicularis ducitur sit pollicum 11½, centro eodem, ubi & Sol collocandus, cir|culumGa naar margenoot+ Eclipticae signorum descripsimus radio pollicum 10⅔. Hunc circulum in partes 360 partiti sumus, Signaque 12 suis locis adscripsimus, collocato Arietis signo in parte, quae spectanti ad dextram est, ac pari cum centro altitudine. Porro Apheliorum loca in laterculo adjecto notata, in quam partem uniuscujusque Planetariae orbitae centrum sumptum fuerit, declarat. Ex proportione vero semidiametrorum juxta collocata etiam mensura harum linearum intelligitur, si una ipsarum quae est orbitae Telluris semidiameter desinita fuerit, quam quidem pollicis unius statuimus, seu pedis Rhenolandici duodecimam partem, qualium enim haec partes 100000 continere censetur, talium radii orbitarum caeterarum partes in laterculo descriptas habent. Earundem quoque partium sunt excentricitates hic adnotatae, quas ex centro Eclipticae, ubi locus Solis, versus Apheliorum loca accipere oportet, atque ibi centra cujusque orbitae signare. Ita ex. gr. Saturni orbitam descripturus initio Anni Christi 1682. lineam ex Eclipticae centro duco ad Sagittarii grad. 27, scr. 40′. in ea pono ex centro eodem particulas 54, qualium semidiameter orbitae telluris sive pollex unus 100 continet, non possumus enim in hac parvitate ulteriores minutias prosequi. Ita centrum orbitae Saturni reperio. Tum deinde accepto semidiametro partium earundem 951, orbitam Planetae describo, cujus Aphelium signo litera Λ ad intersectionem rectae ejus, quam ex centro ductam ostendi. Cum vero orbitae Planetariae in coelo omnes non nihil declinent a plano Eclipticae seu plano orbitae telluris, quod planum hic ipsius tabulae superficies esse intelligitur; ut nimirum dimidiâ sui parte supra attollantur, altera dimidia infra descendant, perspicuum est, non esse ipsas Plane|tarum orbitas, quae a nobisGa naar margenoot+ sunt descriptae, sed lineas ejusmodi in quas incidunt ductae in Eclipticae planum per pendiculares ex orbitarum quibuslibet punctis, quas tamen lineas pro orbitis ipsis habemus, quod secundum illas Planetae motus in longitudinem examinetur; revera autem sunt orbitae ad Eclipticae planum reductae. Itaque puncta bina, quibus orbita quaeque | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 622]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nous avons indiqué par leurs signes ☊ et ☋ les deux points, appelés noeuds où chaque orbite coupe le plan de l'écliptique, signes dont le premier est attribué au noeud ascendant, celui à partir duquel la planète va du côté boréal par rapport à l'écliptique, côté qui doit être censé se trouver au dessus de la table, le second au noeud descendant, c.à.d. au point où la planète passe dans l'hémisphère austral. Ces noeuds se trouvent suivant le sentiment universel des astronomes opposés l'un à l'autre sur une droite passant par le centre du soleil, quoique ceci ne semble pas être tout-à-fait exact, comme nous le dirons plus amplement en un lieu propreGa naar voetnoot20). Ici nous avons marqué dans un tableau les lieux des noeuds ascendants ainsi que les angles ou inclinaisons des plans des orbites planétaires par rapport à celui de l'écliptique, d'après les auteurs qui nous semblent les plus dignes de foi, e.a. en faisant usage pour Vénus et Mercure des résultats les plus récents d'observateurs qui ont vu passer ces planètes sur le disque du soleilGa naar voetnoot21). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pour le 1 janvier de l'année 1682Ga naar voetnoot22)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 623]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
planum Eclipticae intersecat (hi nodi vocantur) suis signis ☊ & ☋ notavimus, quorum illud nodo ascendenti tribuitur, unde nimirum Planeta ad partes Eclipticae boreas feratur, quas supra tabulam existere intelligendum; alteram nodo descendenti, quo praeterito in partes austrinas transeat. Hi vero in eadem linea recta per Solis centrum ducta oppositos locos obtinent communi Astronomorum consensu, etsi non plane ad amussim res sese hoc modo habere videatur, ut suo loco amplius declarabiturGa naar voetnoot18). Caeterum loca nodorum ascendentium; Et quali angulo plana orbitarum Planetarum ad Eclipticae planum inclinentur in tabella hic expressimus; auctores eos secuti qui maxime nobis probandi videntur; adeoque in Venere & Mercurio recentissimorum adhibitis observationibus, quibus in Sole ipso hi Planetae apparueruntGa naar voetnoot21).| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Anno 1682. Januarii 1mo.Ga naar voetnoot22)Ga naar margenoot+
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 624]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pour qu'on puisse aussi connaître les latitudes apparentes des planètes nous avons décrit de part et d'autre sur la ligne droite qui joint les noeuds opposés des arcs de circonférence de cercle, l'un en dehors de la partie septentrionale de l'orbite, l'autre en dedans de sa partie méridionale, lesquels ont chacun à la partie nommée correspondante, là où la distance est la plus grande, une distance égale à celle qu'en ces endroits l'orbite elle-même devrait avoir de l'écliptique, étant située soit au dessus soit au dessous de son plan; nous avons marqué en ces endroits les angles d'inclinaison. Mais lorsque la planète se trouve en un point quelconque de la projection de son orbite, et qu'on prend la plus courte distance de ce point à l'arc adjoint, celle-ci indiquera avec une grande approximation la distance de la véritable orbite de la planète au plan de l'écliptiqueGa naar voetnoot27), et en comparant cette distance avec celle de la planète à la | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 625]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Porro ut apparentes Planetarum latitudines cognoscere liceat super linea recta nodos oppositos jungente arcus circunferentiae circularis utrinque descripsimus, alterum extra orbitae portionem boream, alterum intra portionem australem, tanto intervallo ab ipsis portionibus, ubi maxime absunt, recedentes, quanto orbita ipsa supra atque infra planum Eclipticae iis ipsis in locis extare deberet; atque ibidem angulos inclinationis adscripsimus. In quocunque vero orbitae suae reductae puncto Planeta reperietur, si ab eo puncto ad adscriptum arcum minima distantia accipiatur, ea quam proxime intervallum indicabit, quo ab Eclipticae plano illic vera Planetae orbita receditGa naar voetnoot27), quod intervallum cum distantiâ Planetae a Tellure comparando, ipse quo|que latitudinis angulus exGa naar margenoot+ triangulorum doctrina facile investigabiturGa naar voetnoot28); atque haec de exteriore Automati forma deque usu ejus dixisse sufficiat: Nunc ad inferiorem fabricam pergamus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 626]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
terre, l'angle de la latitude pourra facilement être calculé par voie trigonométriqueGa naar voetnoot28). Qu'il suffise d'avoir dit ce qui précède sur la forme extérieure de l'automate et sur son usage. Occupons-nous maintenant de l'agencement intérieur. Les nombres des dents des roues ont été trouvés de la manière suivante. Nous avons comparé entr'eux le mouvement moyen annuel, ou de 365 jours, de chaque planète sous l'écliptiqueGa naar voetnoot29) avec le mouvement moyen annuel de la terre, tels que l'un et l'autre sont consignés dans les tables astronomiques, en réduisant les mouvements dans les arcs entiers en tierces ou soixantièmes parties de secondes. Comme les nombres ainsi obtenus ont entr'eux la même proportion que les arcs des circonférences de cercle décrits simultanément dans leurs orbites par la planète considérée et par la terre, il s'ensuit que les périodes de l'une et de l'autre sont exprimées par le contraire du même rapport, lequel doit donc aussi, à moins que l'on ne prenne le même rapport exprimé par des nombres plus petits, être celui des dents des roues, savoir d'une part la roue planétaire, d'autre part la roue montée sur le grand axe laquelle engrène avec elle. En effet, par chaque révolution de l'axe la Terre parcourt son orbite entière, puisque nous donnons des nombres de dents égaux à la roue qui porte la Terre et à celle de l'axe qui lui correspond, p.e. 60 ou tel autre nombre qui leur convient. Toute la question se réduit donc à ceci: étant donnés deux grands nombres ayant entr'eux un certain rapport, en trouver d'autres plus petits pour les dents des roues qui ne soient pas incommodes par leurs grandeurs et qui aient entr'eux à peu près le même rapport, de telle façon qu'aucun couple de nombres plus petits ne fournisse un rapport plus approchant de la vraie valeur. Mais nous rendrons la chose plus claire par un exemple. Supposons donc qu'il faille trouver les dents de la roue de Saturne et celles de la roue plus petite, indiquée par la lettre K dans la Fig. 144, qui la meut et est elle-même montée sur l'axe. Le mouvement annuel de Saturne - je me base tant ici qu'ailleurs sur les plus récentes Tables de Riccioli - est dit avoir la valeur 12o 13′34″18‴Ga naar voetnoot30). Celui de la Terre, que Riccioli appelle celui du Soleil, est de 359o45′40″31‴Ga naar voetnoot31). Réduisant l'une | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 627]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dentium in rotis numerus hoc modo a nobis inventus fuit; Motum Medium cujusque sub EclipticaGa naar voetnoot29) Planetae annuum seu dierum 365 ad Telluris Medium annuum motum, quales in Tabulis Astronomicis exhibentur, comparavimus; reductis ad tertios scrupulos arcubus eorum motuum integris. Numeri hinc orti, cum eam inter se proportionem habeant, quam arcus circulorum eodem tempore a Planeta, atque a Tellure in orbitis suis emensi, sequitur tempora utriusque Periodica ejusdem rationis contrariam continere; quam itaque, vel similem minoribus numeris expressam, etiam dentium numeri habere debent, quibus nempe rota tum Planetaria, tum altera ipsi congruens, atque axi magno imposita incidantur; singulis enim axis hujus conversionibus Tellus integram orbitam suam percurrit; quoniam aequalem dentium numerum rotae Tellurem ferenti, itemque ei, quae in axe magno respondet, attribuimus, sexagenarium puta, vel alium pro lubitu, qui commode in rotas inducatur. Huc itaque res tota recidit ut datis numeris duobus magnis certam inter se rationem habentibus, alii minores inveniantur rotarum dentibus multitudine sua non incommodi, quique eandem proxime rationem ita exhibeant, ut nulli ipsis minores propius. Sed exemplo rem totam melius exponemus; Sunto igitur inveniendi dentes in rota Saturni, inque minore illam movente, quae axi magno est imposita, quam indicabat superius litera k. Annuus Saturni motus (sequor autem tum in hoc tum in caeteris Riccioli recentissimas Tabulas) prodi|tus est gr. 12, 13′, 34″, 18‴Ga naar voetnoot30). Annuus Telluris, quem ille SolisGa naar margenoot+ vocat, gr. 359o, 45′, 40″, 31‴Ga naar voetnoot31). Reductis igitur omnibus ad scrupula tertia, fit propor- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 628]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
et l'autre à des tierces, on obtient le rapport 2640858:77708431Ga naar voetnoot32). Par conséquent, comme le dernier nombre est au premier, ainsi est la période de Saturne au temps dans lequel la Terre accomplit sa révolution autour du Soleil; partant le nombre des dents de la roue de Saturne doit avoir, avec la meilleure approximation pratiquement possible, ce même rapport au nombre des dents de sa roue motrice. Pour trouver donc des nombres plus petits qui expriment approximativement ce rapport, je divise le plus grand nombre par le plus petit, puis le plus petit par le reste de la première division et ensuite ce reste par le nouveau reste. Continuant ainsi je trouve que la première division donne 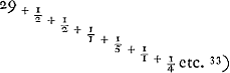 Ga naar voetnoot33) c.à.d. un nombre plus une fraction à numérateur 1 dont le dénominateur possède de nouveau une fraction adjointe à numérateur 1 et dont le dénominateur est composé de la même manière; et ainsi de suite. Poursuivant ce calcul aussi longtemps que possible, on parvient enfin par la division à un reste 1. Or, lorsqu'on néglige à partir d'une fraction quelconque les derniers termes de la série, p.e. ici la fraction ⅕Ga naar voetnoot33) et celles qui la suivent, et qu'on réduit lesautres plus le nombre entier à un commun dénominateur, le rapport de ce dernier au numérateur, sera voisin de celui du plus petit nombre donnéau plus grand; et la différence sera si faible qu'il serait impossible d'obtenir un meilleur accord avec des nombres plus petits. Le mode de la réduction estaisé; en effet, les dernières fractions, par lesquelles nous commençons, savoir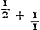
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 629]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tio 2640858 ad 77708431Ga naar voetnoot32). Itaque quam rationem habet posterior horum numerus ad priorem, eam habet Saturni tempus Periodicum ad tempus, quo circa Solem Tellus convertitur, ac proinde & rotae Saturniae dentium numerus ad suae motricis rotae dentes hanc rationem quam proxime servare debet. Inveniendis igitur numeris minoribus qui proxime rationem istam exprimunt; divido majorem per minorem, & rursus minorem per eum qui a divisione relinquitur, & hunc rursus per ultimum residuum, atque ita porro continenter pergendo invenio quod fit ex primâ divisione 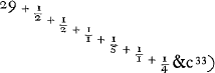 Ga naar voetnoot33) nempe numerum cum adjuncta fractione, cujus fractionis numerator est unitas, denominator vero rursus fractionem adjunctam habet, cujus numerator unitas, denominator similiter ac praecedens componitur; idque ita consequenter; qua via, si, quo usque potest, continuetur, eo devenitur, ut a divisione tandem unitas supersit. Jam ab hac fractionum serie posteriores aliquousque praecidendo, velut hic ⅕Ga naar voetnoot33) cum caeteris deinceps sequentibus, reliquasque cum numero ipsas praecedente reducendo ad communem denominatorem, erit hujus ad numeratorem ratio propinqua ei, quam datorum numerorum minor habet ad majorem; adeo quidem ut minoribus numeris propius ad eam accedere non liceat. | Reductionis modus facilis est; nempeGa naar margenoot+ posteriores, unde hic incipimus fractiones,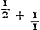 , tantundem valent ac ⅓, unde ad , tantundem valent ac ⅓, unde ad
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 630]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
valent ⅓; passant à celle qui précède immédiatement et réduisant, 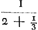 donne 3/7; prenant ensuite avec la fraction le nombre entier et réduisant de nouveau, 29 + 3/7 donne 206/7. Par conséquent le rapport 7:206 est voisin de 2640858:77708431. C'est pour quoi nous avons donné 206 dents à la roue de Saturne et 7 à sa roue motrice. Quant à la thèse qu'il est impossible de trouver des nombres plus petits exprimant le rapport proposé avec une plus grande approximation, nous la démontrerons comme suit. Il est d'abord certain, d'après la Prop. 1 du Livre 7 d'EuclideGa naar voetnoot34), que les nombres résultant d'une réduction de cette espêce sont premiers entr'eux. En effet, notre division continue n'est autre chose que cette soustraction euclidienne, et en l'appliquant à nos nombres 206 et 7 obtenus par la réduction, il est clair qu'on aboutit enfin au reste 1, puisque le numérateur de toutes les fractions est l'unité. Supposé que deux autres nombres fournissent une meilleure approximation au rapport des grands nombres, il est nécessaire, lorsqu'on effectue la division continuelle du plus grand par le plus petit jusqu'à ce qu'il reste 1, qu'ils donnent le quotient 29 avec les mêmes fractions adjointes que plus haut, mais continuées outre le terme d'où nous étions partis dans notre réduction qui nous faisait trouver les nombres 7 et 206. En effet, il est impossible de s'approcher davantage d'une autre manière du quotient de la première
division lequel comporte toutes les dites fractions jusqu'au bout de la série. Il serait donc nécessaire, vu que la division continue de 206 par 7 donne donne 3/7; prenant ensuite avec la fraction le nombre entier et réduisant de nouveau, 29 + 3/7 donne 206/7. Par conséquent le rapport 7:206 est voisin de 2640858:77708431. C'est pour quoi nous avons donné 206 dents à la roue de Saturne et 7 à sa roue motrice. Quant à la thèse qu'il est impossible de trouver des nombres plus petits exprimant le rapport proposé avec une plus grande approximation, nous la démontrerons comme suit. Il est d'abord certain, d'après la Prop. 1 du Livre 7 d'EuclideGa naar voetnoot34), que les nombres résultant d'une réduction de cette espêce sont premiers entr'eux. En effet, notre division continue n'est autre chose que cette soustraction euclidienne, et en l'appliquant à nos nombres 206 et 7 obtenus par la réduction, il est clair qu'on aboutit enfin au reste 1, puisque le numérateur de toutes les fractions est l'unité. Supposé que deux autres nombres fournissent une meilleure approximation au rapport des grands nombres, il est nécessaire, lorsqu'on effectue la division continuelle du plus grand par le plus petit jusqu'à ce qu'il reste 1, qu'ils donnent le quotient 29 avec les mêmes fractions adjointes que plus haut, mais continuées outre le terme d'où nous étions partis dans notre réduction qui nous faisait trouver les nombres 7 et 206. En effet, il est impossible de s'approcher davantage d'une autre manière du quotient de la première
division lequel comporte toutes les dites fractions jusqu'au bout de la série. Il serait donc nécessaire, vu que la division continue de 206 par 7 donne
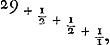
que par les divisions du même genre correspondant aux nombres plus approchés, une fraction au moins fût ajoutée à celles-ci, soit ⅕ soit une autre, pour pouvoir se rapprocher du quotient universel mieux qu'en s'arrêtant à 1/1. Mais il résulte manifestement de cette conclusion que les nombres deviennent plus grands par cette réduction que lorsqu'on part d'une fraction antérieure, puisque par l'adjonction de chaque fraction réduite on obtient une fraction composée de nombres premiers entr'eux et qui par conséquent ne peut être réduite à d'autres plus petits, ce qui deviendra évident pour celui qui examine la chose en ayant égard au théorème suivant aisément démontrable: étant donnés deux nombres premiers entre eux, chacun d'eux est premier à la somme de lui-même ou d'un multiple de lui-même et de l'autre nombre. En effet, s'il n'en était pas ainsi, le nombre considéré mesurerait le nombre composé; or, il en mesure | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 631]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
proxime praecedentem pergendo ac reducendo 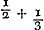 , faciunt 3/7; denique & numerum integrum includendo ac reducendo 29+3/7, siunt 206/7. Itaque numeri 7 ad 206 propinqua ratio est rationis 2640858 ad 77708431. Eoque rotae Saturniae dentes 206 dedimus, ipsam vero moventi dentes 7. Quod autem minores numeri non inveniuntur, qui propius rationem propositam exprimant, ita ostendemus. Principio certum est numeros hujusmodi reductione factos, esse inter se primos, ex Prop. 1. l. 7. Elem.Ga naar voetnoot34) quia nihil aliud est divisio nostra continua quam subtractio illa Euclidea, quae si numeris nostris 206 & 7, reductione effectis adhibeatur, planum est unitatem tandem relinqui, quia fractionum istarum omnium numerator est unitas. Quod si jam duo quivis alii numeri propius ad proportionem magnorum accedunt, eos necesse est, facta continua divisione majoris per minorem, donec unitas supersit, quotientem efficere 29, cum fractionibus iisdem, quae supra, continue adjectis, atque ulterius continuatis quam unde reductionem incepimus, cum inveniremus numeros 7 & 206. alioqui enim ad primae divisionis quotientem qui dictas fractiones omnes quousque possunt continuatas adjectas habet propius accedi nequit. Sic quoniam continua divisione 206 per 7, invenitur , faciunt 3/7; denique & numerum integrum includendo ac reducendo 29+3/7, siunt 206/7. Itaque numeri 7 ad 206 propinqua ratio est rationis 2640858 ad 77708431. Eoque rotae Saturniae dentes 206 dedimus, ipsam vero moventi dentes 7. Quod autem minores numeri non inveniuntur, qui propius rationem propositam exprimant, ita ostendemus. Principio certum est numeros hujusmodi reductione factos, esse inter se primos, ex Prop. 1. l. 7. Elem.Ga naar voetnoot34) quia nihil aliud est divisio nostra continua quam subtractio illa Euclidea, quae si numeris nostris 206 & 7, reductione effectis adhibeatur, planum est unitatem tandem relinqui, quia fractionum istarum omnium numerator est unitas. Quod si jam duo quivis alii numeri propius ad proportionem magnorum accedunt, eos necesse est, facta continua divisione majoris per minorem, donec unitas supersit, quotientem efficere 29, cum fractionibus iisdem, quae supra, continue adjectis, atque ulterius continuatis quam unde reductionem incepimus, cum inveniremus numeros 7 & 206. alioqui enim ad primae divisionis quotientem qui dictas fractiones omnes quousque possunt continuatas adjectas habet propius accedi nequit. Sic quoniam continua divisione 206 per 7, invenitur
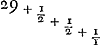
necesse esset divisione simili numerorum propiorum unam saltem insuper fractionem istis adjici, vel ⅕ vel aliam qua propius ad quotientem universalem pervenia|tur, quamGa naar margenoot+ si ad 1/1 subsistamus. Hinc vero facta reductione, manifestum est, numeros majores effici, quam si a citeriori fractione caeptum fuisset, quandoquidem accessione cujusque fractionis reductae efficitur fractio constans numeris inter se primis, quaeque propterea ad minores reduci nequit; quod examinanti manifestum fiet si ad sequens theorema attenderit demonstratu facillimum: nempe Propositis duobis numeris inter se primis, eorum alteruter ad se ipsum vel sui multiplicem altero numerorum auctum primus erit. Si enim non, ergo ita compositum metietur, sed & partem metitur, hoc est, se ipsum, vel | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 632]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
aussi une partie, c.à.d. soi-même ou son multiple; il mesurera donc aussi le reste; ce qui est absurde, puisque les nombres étaient par hypothèse premiers entre eux. Les nombres plus rapprochés du rapport proposé ne seront donc pas plus petits mais au contraire plus grands que les nombres trouvés 206 et 7. On conçoit en outre facilement que la réduction des fractions commence toujours plus utilement d'une d'elles qui est suivie par une fraction possédant un dénominateur assez grand par rapport à ceux des fractions environnantes; c'est ainsi que dans l'exemple proposé nous avons commencé la réduction là où suivait la fraction ⅕. Or, l'utilité de cette méthode s'étend à beaucoup d'autres cas où il s'agit de remplacer un rapport numérique donné par un autre composé de nombres plus petits. P.e. celui où le rapport de la circonférence du cercle à son diamètre est donné en un grand nombre de chiffres exacts, mettons 31415926535 à 10000000000. Ici la division donne 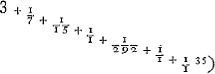 et en commençant la réduction en partant de la fraction 1/7 on obtient la proportion d'Archimède 22 à 7; mais en commençant par 1/1 il en résulte celle beaucoup plus approchée qu'Adr. Metius a fait connaître, savoir 355:113, en effet, comme 113 est à 355, ainsi est 10000000 à 31415929 etc. De la même manière on peut trouver d'autres rapports plus approchants de la vraie valeur, mais celui de Metius est d'un excellent usage et fort exact eu égard à la petitesse des nombres, ceci à cause del'exiguité de la fraction 1/292 qui suit celle par où l'on a commencé la réduction. C'est là une particularité qu'on ne rencontre pas facilement en faisant des essais avec d'autres nombres. Il faut savoir en outre que par notre réduction on trouve tour-à-tour un terme plus grand et un terme plus petit que le véritable; le terme est plus grand lorsque la réduction a été commencée par la première, la troisième ou la cinquième fraction ou plus généralement par une fraction d'ordre impair. P.e. lorsque dans le cas précédent nous commencions la réduction en partant de la troisième fraction 1/1, la proportion trouvée de la circonférence au diamètre 355:113 devenait plus grande que la vraie valeur. Mais si j'avais commencé par la deuxième fraction, il en serait résulté le rapport 333:106 inférieur à la vraie valeur. Commençant par la première fraction, savoir 1/7, on trouve de nouveau un rapport, celui d'Archimède, 22:7, supérieur à la véritable | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 633]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sui multiplicem; ergo & reliquum metietur; quod absurdum, quandoquidem numeri inter se primi ponebantur. Itaque propiores numeri proportioni propositae, non minores, sed majores erunt inventis 206 & 7. Porro facile intelligitur reductionem fractionum ab ea utilius semper incipi, quam proxime insequens fractio majorem denominatorem habebit vicinarum comparatione; sicut & antecedenti exemplo inde reductionem incepimus, ubi ⅕ sequebatur. Utilitas vero methodi ad alia multa porrigitur, ubi proportio quaepiam numeris comprehensa ad proxime aequalem aliis minoribus numeris est redigenda. Velut cum peripheriae circuli ad diametrum ratio ad notas veras plures datur, nempe quae 31415926535 ad 10000000000. Hîc facta divisione fit, 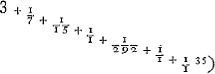 ubi si reductionem inchoaremus a fractione 1/7 fit proportio Archimedea 22 ad 7, si vero ab 1/1 fit alia multo propinquior quam Adr. Metius prodidit 355 ad 113; sicut enim | 113Ga naar margenoot+ ad 355 ita 10000000 ad 31415929 &c. Eodem modo hic alias ad verum propius accedentes rationes invenire licet; sed haec Metiana, cum ad usum habilis est, tum pro numerorum parvitate eximia, ob exiguam particulam 1/292 citra quam reductio coepta est; Cujusmodi non facile similis reperitur ulteriores numeros tentanti. Sciendum vero, reductione hac nostra majorem proportionis terminum alternis majorem minoremve vero reperiri, prout a prima, tertia, quinta aut alia deinceps impari fractione reductio inchoata fuerit. Ita cum a tertia fractione, quae est 1/1 reductionem praecedentem inceperimus, fit proportio circumferentiae ad diametrum, ut 355 ad 113 major vera; at si a secunda quae est 1/15 incepissem, extitisset inde proportio 333 ad 106 minor verâ; rursus si a prima quae est 1/7 initium fiat oritur proportio Archimedea 22 ad 7 major | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 634]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
proportion; j'appelle ici véritable celle qui s'exprime par les grands nombres donnés, laquelle nous avons prise comme représentant vraiment le rapport de la circonférence au diamètre. La démonstration de cette propriété repose sur ce fondement fort connu que toute fraction devient plus petite par l'augmentation du dénominateur et plus grande par sa diminution. En effet, soit A le nombre résultant de la première division et qu'il y ait ensuite un nombre quelconque de fractions descendantes B, C, D, E, F, au dénominateur de la dernière desquelles soit jointe une fraction Z obtenue par la réduction de toutes les fractions ultérieures. Comme la fraction indiquée par F est par conséquent plus grande que la vraie fraction, puisqu'elle possède un dénominateur inférieur au vrai dénominateur qui serait 1 + Z, il résulte de l'augmentation du dénominateur de la fraction E par la fraction F une fraction réduite, provenant de E et de F, plus petite que la vraie fraction; partant en augmentant ensuite le dénominateur de la fraction D, il résultera de la réduction de celle-ci une fraction provenant de D, E et F qui sera plus grande que la vraie valeur; et en augmentant enfin le dénominateur de la fraction C par cette dernière, une fraction sera produite, provenant de C, D, E et F, qui sera plus petite que la fraction véritable. Puisque les fractions obtenues par la réduction de celles qui forment la série ascendante sont donc nécessairement alternativement plus grandes et plus petites que les fractions véritables, et que la plus basse, par laquelle on commence, est toujours trop grande, il appert facilement que si celle-ci occupe un lieu impair, la fraction résultant de la réduction de toutes les fractions sera également trop grande et que par conséquent elle donnera, étant ajoutée au nombre A, un rapport supéricur au rapport véritable. Mais si celle par laquelle on commence est d'ordre pair, il est clair que de la réduction de toutes les fractions il en résultera une qui sera inférieure à la fraction véritable et que par conséquent elle fournira, lorsqu'on l'ajoute au nombre A, un rapport inférieur au rapport véritable. La vérité de la proposition est dès lors manifeste. Il faut savoir en outre que si l'on désire avoir la série consécutive de tous les termes approchants de la proportion donnée, il faut faire la réduction d'abord pour toutes les fractions d'ordre impair, ensuite pour toutes celles d'ordre pair, et cela en prenant successivement dans le cas de toutes les fractions à dénominateurs supérieurs à 1 des dénominateurs variant de 1 jusqu'au vrai dénominateur et en effectuant la réduction pour chacune des fractions ainsi obtenues. En agissant ainsi pour les fractions d'ordre impair, on obtiendra en bon ordre tous les termes supérieurs à la vraie valeur; dans le cas des fractions d'ordre pair on trouvera, également en bon ordre, tous les termes inférieurs à la valeur véritable. C'est ainsi que dans l'exemple proposé plus haut il faut à la première fraction substituer successivement 1/1, ½, ⅓, ¼, ⅕, ⅙, 1/7; la réduction donnera alors les rapports tous supérieurs au vrai rapport 4:1, 7:2, 10:3, 13:4, 16:5, 19:6, 22:7. Commençant ensuite par la troisième fraction D, le prochain rapport supérieur trouvé sera 355:113. Et en commençant par la cinquième | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 635]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
vera; veram autem proportionem hic appello, quae iis, qui adsumti sunt, magnis numeris exprimitur, quam nimirum pro ipsa proportione circumferentiae ad diametrum accepimus. Horum vero demonstratio hoc fundamento nititur notissimo, Fractionem quamcunque, aucto denominatore, fieri minorem; imminuto, majorem. Sit enim numerus ex prima divisione ortus a, fractionibus vero deinceps descendentibus quotlibet bcdef & ad infimae f denominatorem adjecta intelligatur fractio quae ex omnibus ulterioribus fractionibus reductis conficeretur, quae dicatur z. Cum itaque fractio, cui superscriptum f, sit major vera, quia denominatorem habet minorem vero denominatore, qui esset 1 + z, hinc augendo denominatorem fractionis e fractione f, fiet reducta fractio ex fractionibus e, f, minor vera, ideoque rursus augendo denominatorem fractionis d, ista fractione re|ducta, fiet fractio ex def reductis major vera,Ga naar margenoot+  ac proinde rursus augendo denominatorem fractionis c ista ultima, fiet fractio, ex cdef fractionibus reductis, minor vera. Cumque ita necessario fractiones ex reductione fractionum sursum tendendo effectae, alternatim nunc majores, nunc minores evadant Veris, sitque infima, unde initium fit, semper vera major; facile apparet, si haec sedem imparem obtineat, etiam ex omnium fractionum reductione effectam vera majorem fore, ideoque numero a additam, daturam terminum proportionis majorem vero. Si vero illa, unde initium fit, sedem parem obtineat, tum ex reductione omnium exstituram vera minorem, ac proinde numero a additam, daturam terminum proportionis vero minorem. Quare patet propositi veritas. Sciendum porro, si omnes ordine terminos proximos datae proportioni desideremus, tunc & ab omnibus fractionibus imparium sedium, & rursus ab omnibus sedium parium faciendam reductionem, idque ita, ut pro singularum fractionum denominatore, qui unitate major erit, ponantur seorsim denominatores omnes ab unitate ad illum usque, & cum iis singulis reductio inchoetur perficiaturque. Hoc enim si fiat in fractionibus sede impari locatis, omnes termini veris majores ordine existent; si verò fiat in fractionibus sedium parium, habebuntur ordine omnes termini veris minores. Ita in proposito exemplo si pro fractione prima 1/7 ponantur sigillatimGa naar voetnoot*) 1/1, ½, ⅓, ¼, ⅕, ⅙, 1/7, facta hinc reductione existent proportiones vera majores: 4 ad 1, 7 ad 2, 10 ad 3, 13 ad 4, 16 ad 5, 19 ad 6, 22 ad 7. deinde a fractione tertia d incipiendo fiet | proxima ratioGa naar margenoot+ major 355 ad 113. Et ab quinta f incipiendo fiet proxima ratio major 104348 ad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 636]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
F, le prochain rapport supérieur sera 104348:33215. Lorsque d'autre part à la deuxième fraction 1/15 on substitue toutes les 15 fractions 1/1, ½, ⅓ etc. et de même à la quatrième 1/292 toutes les fractions depuis l'unité 1/1, ½, ⅓ jusqu'à 1/292, on obtiendra en bon ordre après réduction de chacune d'elles des rapports inférieurs à la vraie valeur, ceux bien entendu qui se peuvent avoir à l'aide de la fraction E. Si nous voulons enfin construire une série mixte continue, savoir une série contenant tant des termes supérieurs que des termes inférieurs à la vraie valeur, dont chacun soit plus approchant que le terme précédent, il saut s'en tenir à la règle suivante: dans chaque fraction à dénominateur supérieur à 1 il faut substituer successivement, non pas comme tantôt, tous les dénominateurs plus petits depuis l'unité, mais seulement tous les dénominateurs depuis le plus petit nombre qui surpasse la moitié du vrai dénominateurGa naar voetnoot36). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 637]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
33215. Rursus si pro fractione secunda 1/15 ponantur sigillatimGa naar voetnoot*) 15 fractiones 1/1, ½, ⅓, &c. Item pro quarta 1/292 ponantur omnes ab unitate, 1/1, ½, ⅓, usque ad 1/292; factis reductionibus habebuntur ordine proportiones veris minores, quae quidem ad fractionem E procedendo dari possint. Quod si denique seriem continuam mixtam terminorum tam majorem quam minorem vera proportionem exhibentium velimus, quorum quique praecedentibus ad veram propius accedant, tunc hoc observandum, ut in fractionibus quibusvis, quarum denominator unitate major erit, ponantur, non ut modo factum omnes deinceps minores denominatores ab unitate, sed ab ea incipiendo quae dimidio illius denominatoris proxime major eritGa naar voetnoot36). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 638]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nous servant de cette méthode aussi pour les autres planètes, nous avons donné 166 dents à la roue de Jupiter, 14 dents à sa roue motriceGa naar voetnoot37); 158 dents à la roue de Mars, 84 dents à sa roue motriceGa naar voetnoot38); 32 dents à celle de Vénus, 52 à sa roue motrice, nombres qui sont à peu près entre eux comme 43:70Ga naar voetnoot39). Si nous nous étions servi de ces derniers et que nous avions donné 43 dents à la roue de Vénus, 70 à sa roue motrice montée sur le grand axe, la machine aurait correspondu un peu plus exactement au vrai mouvement de Vénus; en effet, les premiers nombres, ceux dont nous avons fait usage, sont cause pour Vénus d'un retard de 3o 37′ en 20 ans, tandis que les seconds auraient légèrement fait avancer la planète en ces mêmes 20 ans, savoir d'un peu moins de 15′ seulement. C'est aussi à peu près de la même manière qu'ont été trouvées les dents des pignons qui meuvent Mercure: prenant 365 jours, 5 heures, 49′ 15″ 4‴ pour la période de la terre sous l'écliptiqueGa naar voetnoot40) et 87 jours, 23 heures, 14′ 24″ pour celle de Mercure sous elleGa naar voetnoot41), ou plutôt, pour la facilité du calcul, respectivement 365 jours, 5 heures, 50′ et 87 jours, 23 heures, 15′Ga naar voetnoot41), on trouvera pour le rapport des révolutions de Mercure à celles de la Terre 105190:25335 ou 21038:5067, par la division desquels nombres, exécutée suivant la méthode susdite, il vient  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 639]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hac igitur ratione in caeteris quoque Planetis usi, rotae Jovis dedimus dentes 166, rotae vero ipsam moventi dentes 14Ga naar voetnoot37), rotae Martis dentes 158, ipsam vero moventi dentes 84Ga naar voetnoot38). Rotae Veneris dentes 32, ei quae movet dentes 52; qui numeri sunt inter se ferme, ut 70 ad 43Ga naar voetnoot39). Quibus numeris si usi essemus, & Rotae Veneris dedissemus dentes 43, rotae vero hanc in axe magno agitanti, 70, aliquantulum perfectius vero Veneris motui respondisset Machina. Priores enim numeri, quos adhibuimus, efficiunt, ut Venus post 20 annos a vero loco deficiat gr. 3, 37′. cum posteriores in iisdem 20 annis tantillulum ultra verum locum Venerem promoveant, sed excessu 15′. non plene aequante. Nec multum dissimili ratione inveniuntur dentes rotularum, quae Mercurium movent. Assumta enim Periodo telluris sub Ecliptica dierum 365. hor. 5. 49′. 15″. 46‴.Ga naar voetnoot40), Mercurii vero sub eadem dierum 87. Hor. 23, | 14′, 24″, aut facilitatis ergoGa naar margenoot+ assumta illa d. 365. hor. 5. 50′ & hac dierum 87. Hor. 23. 15′.Ga naar voetnoot41) invenietur ratio revolutionum Mercurii ad illas Telluris ut 105190 ad 25335, sive 21038 ad 5067; quorum divisione, eo, quo dictum, modo, instituta 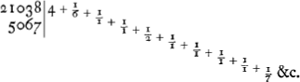 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 640]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Négligeant la dernière fraction et réduisant les autres à un commun dérnominateur on obtient 847/204, lesquels nombres correspondent aussi exactement que possible à la proportion des mouvements des deux planètes considérées. Mais comme 847 est le produit de 121 par 7 et 204 celui de 12 par 17, nous avons donné 12 dents à la roue annuelle qui se trouve sur l'axe commun, et nous avons fait usage de l'interposition (voyez la Fig. 141) d'un axicule mobile autour de deux points fixes situés l'un sur l'axe passant par le Soleil et l'anneau de Mercure, l'autre sur la colonne dressée sur la plaque sixe de la Terre. Ces points sont si éloignés des orbites de Mercure et de Vénus que les dents des roues de Vénus et de la Terre, passant librement sous l'axicule, n'en éprouvent dans leur mouvement aucune gêne. Le dit axicule porte deux pignons, un à chaque extrémité, dont le premier, qui engrène dans la roue annuelle, a 12 dents, tandis qu'il y en a 7 à l'autre engrenant dans la couronne dentée menant la planète, couronne qui possède, elle, 17 dents. Il est évident par là qu'entre le mouvement de l'axe commun et celui de la roue qui mène Mercure, existe le rapport nommé, celui de 204 à 847. Pour établir les nombres des dents des rouages qui mènent la LuneGa naar voetnoot42), nous prenons ici aussi pour le même mouvement annuel 365 jours, 5 heures, 50′ et pour celui de la Lune 29 jours, 12 heures, 44′ 3″ ou plutôt 45′ pour la facilité du calcul, d'où l'on trouvera pour le rapport des révolutions de la Lune à celles de la Terre 105190:8505 ou 21038:1701; en divisant comme auparavant il en résulte 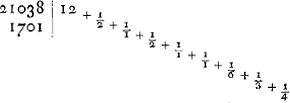 Prenant ⅙ comme dernière fraction et réduisant les précédentes au même dénominateur, on obtient les nombres 1546 et 125; mais comme le premier de ces deux n'a pas de parties aliquotes autres que 2 et 773 qui serait un nombre de dents excessif, il sera préférable de prendre, au lieu de ⅙, la fraction plus petite la plus proche, savoir 1/7, d'où résultent les nombres 1781 et 144, dont le premier est le produit de 137 par 13 et le deuxième celui de 12 par 12. On verra aisément qu'à ces nombres correspondent les rapports sus-énoncés des dents de la roue majeure et des axicules dentés. Il est manifeste d'après la méthode de calcul du nombre des dents, tant de celles qui doivent être taillées dans l'axe commun que de celles qu'il faut tailler dans chacune | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 641]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
& neglecta ultima fractione reliquis ad communem denominatorem deductis fiet 847/204, qui numeri proportioni motuum, quibus hi Planetae moventur, quam proxime respondent. Verum cum 847 fiat ex ductis in se numeris 121, & 7, & 204 ex ductis in se numeris 12 & 17, rotae annuae, quae est in axe communi, inditi sunt dentes 121, & axiculus interpositus rotatilis circa duo puncta fixa, quorum alterum est in axe per Solem & annulum Mercurii transeunte; alterum in columella inhaerente lamellae fixae Telluris. Sunt autem haec puncta ita remota ab ipsis orbitis Mercurii & Veneris, ut dentes rotarum Veneris & Telluris libere sub axiculo transeuntes ab eo in motu suo non impediantur; Hic autem axiculus duas rotulas habet circa unamquamque extremi tatem unam, quarum altera, cujus dentes committuntur rotae annuae, est dentium 12; altera vero, quae armillae dentatae Planetam vehenti committitur dentium 7, cum ipsa armilla habeat dentes 17. quo ipso inter motum axis communis, & rotae Mercurium vehentis eandem proportionem servari, quae est 204 ad 847, manifestum est.| Rotularum, quae Lunam vehunt dentes ut invenianturGa naar voetnoot42), assumto eodem motu annuoGa naar margenoot+ d. 365. hor. 5.50′, & Lunari motu d. 29 hor. 12,44′, 3″ sive scrupulorum 45, ob faciliorem calculum invenietur ratio revolutionum Lunae ad eas Telluris, ut 105190 ad 8505, sive 21038 ad 1701: quibus numeris, ut prius, divisis fit 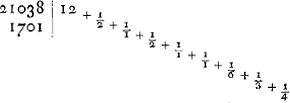 Quod si pro ultima fractione sumatur ⅙, & praecedentes ad eundem denominatorem deducantur, fient numeri 1546 & 125, quorum cum prior nullas partes aliquotas habeat, praeter 2 & 773; hic autem nimium dentium numerum faciat, praestabit si loco fractionis ⅙ proxime minorem sumamus 1/7, quo facto orientur numeri 1781 & 144, quorum prior sit ex 137 & 13, posterior ex 12 in 12. Ex quibus descripta ratio dentium tum in majori rota, tum in minoribus axiculis dentatis facile constabit. Ex ipsa autem hac inventione numeri dentium, qui tum in axe communi, tum in rotis singulos Planetas deferentibus incidi debent, manifestum est non posse has cir- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 642]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
des roues menant les planètes, que les rotations ne peuvent se saire sans que dans le cours du temps de petites fautes se produisent dans les rapports du mouvement de la terre à celui de chaque planète, tels que nous les avons adoptés comme véritables d'après les observations. Or, il est facile de déterminer les grandeurs de ces petites aberrations. En effet, pour que la machine reproduisìt exactement le rapport correspondant au vrai mouvement, il serait nécessaire que ce rapport correspondìt précisément aux nombres des dents des roues. Pour rendre la chose plus claire, considérons par exemple le cas de Saturne. Dans la roue de Saturne montée sur l'axe commun il y a 7 dents, dans celle qui mène la planète il y en a 206. Nécessairement Saturne accomplit donc 7 fois sa révolution en un espace de 206 ans. Mais comme le rapport du mouvement de la Terre à celui de Saturne est exprimé par 7708431:2640858, on trouvera qu'en 206 ans Saturne accomplit son mouvement périodique non pas précisément sept fois, mais environ 7 1/1346 fois. Dans chaque période de 206 ans Saturne retarde donc d'après le mouvement de notre machine de 1/1346 de sa circonférence de cercle, et dans chaque année séparément d'une même fraction d'une quelconque de ses dents. En 1346 ans son mouvement retardera d'une seule dent; après ce laps de temps c'est donc d'une dent qu'il faudra faire avancer la roue de Saturne. Or, cette roue consiste en 206 dents constituant un contour circulaire de 360 degrés. À chaque dent correspondent par conséquent 105 minutes; c'est d'autant qu'il faudra faire avancer Saturne après 1346 ans, ce qui fait 1′34″ en 20 ansGa naar voetnoot43). Le même calcul est applicable à toutes les autres planètes. Reste à expliquer de quelle manière les justes inégalités des mouvements résultent des révolutions de nos rouesGa naar voetnoot44). Voici ce que nous avons à proposer à cet effet. Que l'on considère l'orbite planétaire ANP [Fig. 146], ayant C pour centre; soit S le soleil et prenons sur SC le point quelconque E; soit prise CE : ED comme l'excentricité SC est au rayon CA; et décrivons la circonférence de cercle DM du centre E avec le rayon CE. Il faut savoir en outre qu'au cercle AL est immobilement attaché en son centre mobile C le dit cercle DM, pourvu de dents égales perpendiculaires à son plan, lequel cercle tournera donc nécessairemenr autour du centre C. Mettons qu'il se meuve par la rotation uniforme du tympan KH dont l'axe est dirigé vers C et dont les dents engrènent dans la roue DM. Les dents auront les unes sur les autres une prise suffisante, quoiqu'à cause de l'excentricité de cette roue leur ensemble ne fasse pas toujours un angle droit avec l'axe de la roue mobile nommée. Je dis que par ce mouvement la planète se meut inégalement dans son orbite, de telle manière que son mouvement est à fort peu près identique avec le mouvement keplérien. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 643]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cumvolutiones ita fieri, quin tractu temporis aliquantulum ab ea ratione quam motus telluris ad motum uniuscujusque Planetae ex observatis habere assumsimus, aberret; Cujus tamen aberrationis quantitatem, quantula sit, facile est determinare. Nam ut exacte in machina eadem ratio veri motus observaretur, necessum fo|ret, ut ratioGa naar margenoot+ motus praecise numero dentium in rotulis respondeat. Nimirum in Saturni, ut hoc exemplo res plana fiat, rota, quae in axe communi est, dentes sunt 7, in ea vero, quae Saturnum vehit, dentes 206. Necessum igitur est, ut tempore 206 annorum Saturnus periodum suam absolvat septies; Verum cùm ratio motus Telluris ad Saturnum sit, ut 7708431 ad 2640858, invenietur, Saturnum spatio 206 annorum, absolvere periodum suam non praecise septies, sed circiter 7 1/1346. Singulis ergo 206 annis Saturnus in motu suo in hac machina retardatur 1/1346 sui circuli, singulisque annis tantundem uniuscujusque dentis, & annis 1346 retardabitur ejus motus unico dente, quo igitur post id tempus rota Saturni promovenda erit. Haec autem rota cum constet dentibus 206, qui integrum circulum 360 graduum constituunt, unicuique denti praeterpropter respondebunt 105 scrupuli, per quos itaque promovendus erit Saturnus post exactos annos 1346, adeoque post 20 annos 1′ : 3″4Ga naar voetnoot42). Eademque ratio est in caeteris. Restat explicemus quanam ratione ex harum rotarum revolutione debitae motuum anomaliae sequanturGa naar voetnoot44). Hunc in finem sit anp orbita Planetae, cujus centrum c; Sol s; sumaturque in sc punctum e ad lubitum, fiatque, ut excentricitas sc ad radium ca, ita ce ad ed, quo radio ac centro e describatur circulus dm. Intelligatur porro circulo al super centro suo c mobili affixum esse immobiliter circulum dm incisum dentibus aequalibus super circuli plano erectis, qui proinde circulus necessario quoque circa centrum c movebitur. Ponatur autem moveri versatione aequabili tympani kh axem ad c directum habentis, cujusque dentes congruant dentibus rotae dm. Satis enim convenient, etsi ob excentricitatem hujus rotae non semper tympano ad | rectos angulosGa naar margenoot+ subjiciantur: dico hoc motu Planetam inaequaliter ferri in sua orbita, idque ita, ut ejus motus hypothesi Keplerianae proxime aequipolleat. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 644]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
En effet, prenons sur la circonférence de cercle DM décrite du centre E un arc quelconque DO et admettons que les dents de cet arc aient par la rotation du tympan HK dépassé la droite CD; la droite CO coïncidera alors nécessairement avec la droite CAD, non pas cependant de telle manière que le point O serait en D, il se trouve au contraire plus vers l'intérieur en R, vu que CD, qui est égale à la somme de CE et de EO, est plus grande que CO. Aussi grand qu'est l'angle OCD, aussi grand sera donc aussi l'angle duquel la droite CAD a tourné autour du centre C. Si nous prenons ∠ DCT = ∠ DCO, CT sera donc la droite à laquelle CAD est parvenue, de sorte que la planète sera avancée de A jusqu'au point N où la droite CT coupe la circonférence AN décrite du centre C. Quant au cercle DM, puisque le centre E s'est avancé jusqu'en F et que FT a été prise égale à ED, il occupera désormais le lieu du cercle TR. Or, il apparaît par la même égalité des angles OCD et DCT que l'arc DM que la droite CT coupe sur la circonférence ODM est égale à l'arc DO. Si nous tirons la droite ME, l'angle MED sera donc aussi égal à DEO. Par conséquent si l'arc AL est pris d'autant de degrés qu'en contient l'arc DM, et qu'on joint C et L par une droite, celle-ci sera parallèle à EM. Dans les triangles CEM, SCL les angles LCS, MEC seront donc égaux, et les côtés avoisinant ces angles égaux seront dans un même rapport pour les deux triangles. En effet, on a d'après la construction SC : CL = CE : EM, puisque CL = CA et EM = ED. Les angles MCE et LSC seront donc aussi égaux entre eux et par conséquent les côtés CM et SL parallèles. Nous pouvons maintenant démontrer comme suit que par cette rotation des cercles DM et AL la planète placée en A se meut par la circonférence de cercle AL de telle manière que son mouvement correspond à fort peu près avec l'hypothèse de Kepler. Supposons que la planète se soit portée de A en N, l'espace NSA sera alors son anomalie moyenne; mais à cause du parallélisme des droites SL et CN le triangle NSC sera égal au triangle CLN, qui diffère fort peu du secteur CLNGa naar voetnoot45). L'espace CLA, et par conséquent aussi l'arc AL, correspondront donc à l'anomalie moyenne lorsque la planète se sera transportée de A en N. Et si nous considérons AQP comme l'orbite elliptique de Kepler, la planète sera, il est vrai, en Q, c.à.d. au point où NQ, perpendiculaire à AP, coupe l'ellipse AQP, et non pas en N, mais ces ellipses s'écartent si peu de circonférences de cercles que la différence est inapercevable dans notre machine. N sera donc le lieu de la planète dû au mouvement moyen AL, arc qui contient autant de degrés que l'arc DO ou DM. Que si le tympan est placé en un autre endroit quelconque tel que G également distant du centre C vers lequel il est dirigé, et qu'on place sous lui le point D qui sur la roue ODM est le point le plus distant du centre C, plaçant en même temps la planète de nouveau en A, lieu de son aphélie, il appert que | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 645]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sumto enim in circulo dm. centro e descripto quolibet arcu do, ponatur ejus arcus dentes versatione tympani hk pertransiisse rectam cd, erit necessario recta co in recta cad, etsi non ita, ut punctum o sit in d, sed interius in r, cum cd, quae aequalis est duabus ce, eo, major sit, quam co. Quantus igitur est angulus ocd, tantus quoque erit angulus, quo recta cad mota erit circa Centrum c; ideoque si faciamus angulum dct aequalem angulo dco, erit ct recta, in quam promota erit cad, adeo ut Planeta processerit ex a in punctum n, ubi recta ct secat circumferentiam an centro c descriptam. Circulus autem dm centro e promoto in f, factoque ft aequali ed, habebit situm circuli tr. Apparet autem ob eandem angulorum ocd, dct aequalitatem arcum dm, quem recta ct abscindit in circumferentia odm esse aequalem arcui do. Unde juncta me, erit & angulus med aequalis deo. Itaque si fiat arcus al totidem graduum, quot continet arcus dm, jungaturque cl, erit haec parallela em. In triangulis igitur cem, scl erunt anguli lcs, mec aequales, & circa hos aequales angulos latera proportionalia. Est enim ex constructione sc ad cl, ita ce ad em, quoniam cl ipsi ca & em ipsi ed est aequalis. Erunt ergo aequales etiam anguli mce & lsc, ac proinde latera cm, sl parallela. Hac igitur rotatione circulorum dm, al Planetam in a positum ita moveri per circulum al, ut ejus motus quam proxime respondeat Hypothesi Kepleri ita ostendetur: Ponatur Planeta motus ab a versus n, erit spatium nsa anomalia ejus media; atqui propter lineas parallelas sl, cn erit triangulum nsc aequale triangulo cln, quod insensibili | discrimine differt a sectore clnGa naar voetnoot45). Spatium itaque cla, adeoque & arcus alGa naar margenoot+ respondebit anomaliae mediae; promoto Planeta ex a in n. Quod si ponamus aqp esse ellipticam Kepleri orbitam, erit quidem Planeta in q, ubi scilicet nq perpendicularis in ap Ellipsin aqp secat, non in n, sed hae Ellipses tam parum a circulis recedunt, ut differentia in machina animadverti nequeat. Erit itaque n locus Planetae debitus medio motui al, qui arcus tot gradus, ac arcus do sive dm complectitur. Quod si tympanum ponatur quovis alio loco velut in g aeque distante a centro c versus quod tympanum dirigitur, collocetur vero punctum d, quod in rota odm maxime a Centro c distat sub tympano, & Planeta rursus in a loco Aphelii sui, apparet aequali versatione tympani | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 646]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
par des rotations égales du tympan en G et en D, passent les mêmes angles autour du centre C. En quelqu'endroit qu'on place le tympan, le mouvement de la planète deviendra donc inégal suivant la même loi, quoique les dents de la roue DM aient été prises toutes égales; il faut seulement que les dents du tympan K visant directement le point C aient une certaine longueur par l'effet de laquelle elles puissent engrener dans celles de la circonférence DM coupant la droite DC en des points toujours divers; de plus on doit avoir égard à ce que, lorsque la plus longue droite qu'on puisse tirer du centre C à la circonférence DM est placée directement sous le tympan K, la planète soit placée dans l'aphélie de la circonférence ANL. Mais comme dans notre machine tous les tympans sont placés sur un axe unique, celui-ci ne pourra avoir la bonne direction que par rapport aux centres de deux planètes. C'est pourquoi il faut encore examiner comment le même but peut être atteint au moyen de dents inégales. Supposons à cet effet la circonférence DMP coupée en parties égales Da, ab, bM, Mg et qu'à elles toutes des droites soient tirées à partir du point C, savoir Ca, Cb, CM, Cg, alors celles-ci couperont l'orbite ANL de la planète en des parties inégales Ad, de, eN, Nf. De cette façon on trouvera sur la circonférence ANL un nombre de dents inégales égal à celui des dents égales de la circonférence DM. En leur appliquant maintenant le tympan K (car elles s'y adapteront fuffisamment bien quoiqu'ici plus petites et là plus grandes), il arrivera qu'avec le même nombre de dents du tympan K qui faisait d'abord passer les dents de l'arc DM, passent maintenant celles de l'arc AN, d'où résulte que dans l'un et l'autre cas il se produit la même inégalité du mouvement planétaire, savoir celle dont nous avons fait voir qu'elle correspond à fort peu près à l'hypothèse de Kepler.
FIN. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 647]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
in g atque in d eosdem angulos transire circa centrum c. Quare ubicunque collocetur tympanum, eodem ritu motus Planetae inaequalis fiet, licet dentes rotae dm aequales ponantur, modo dentes tympani k directe spectantis ad punctum c aliquam habeant longitudinem, qua committi queant dentibus circuli dm aliis & aliis in punctis secantis rectam dc; & simul observetur, ut posita recta longissima, quae a centro c ad circulum dm duci potest directe sub tympano k, Planeta ponatur in Aphelio circuli anl. Verum cum nostra in machina omnia tympana in uno eodemque axe sint posita, non poterit ille nisi ad duorum Planetarum centra debite collocari; quare porro considerandum est, qui idem per inaequales dentes perfici queat. Quem in finem supponamus circulum dmp in partes aequales da, ab, bm, mg sectum esse, & ad illas singulas duci ex puncto c rectas, ca, cb, cm, cg illae in partes inaequales ad, de, en, nf secabunt orbitam Planetae anl. Qua ratione invenientur in circulo anl totidem dentes inae|quales, quotGa naar margenoot+ aequales positi sunt in circulo dm. Quibus si nunc porro tympanum k applicetur, (satis enim convenient, licet alibi minores, alibi vero majores paulo evadant,) cum eodem numero dentium tympani k, quo transiere prius dentes arcus dm, jam transeant dentes arcus an, fiet, ut simul eadem motus Planetae oriatur inaequalitas, quam Hypothesi Keplerianae proxime respondere ostendimus.
FINIS. |
|