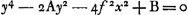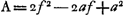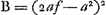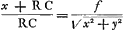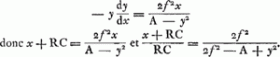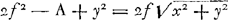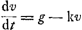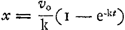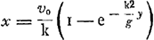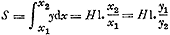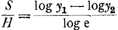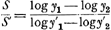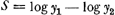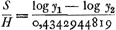Oeuvres complètes. Tome XXI. Cosmologie
(1944)–Christiaan Huygens–
[pagina 451]
| |
Discours de la cause de la pesanteur.Pour trouver une cause intelligible de la Pesanteur, il faut voir comment il se peut faire, en ne supposant dans la nature que des corps qui soient faits d'une mesme matiere, dans lesquels on ne considere aucune qualité ni aucune inclination à s'approcher les uns des autres, mais seulement des differentes grandeurs, figures, & mouvements; comment, disje il se peut faire que plusieurs pourtant de ces corps tendent directement vers un mesme centre, & s'y tienent assemblez à l'entour; qui est le plus ordinaire & le principal phenomene de ce que nous appelons pesanteur. La simplicité des principes que j'admets, ne laisse pas beaucoup de choix dans cette recherche. car on juge bien d'abord qu'il n'y a point d'apparence d'attribuer à la figure, ni à la petitesse des corpuscules, quelque effet semblable à celuy dela pesanteur; laquelle estant un effort, ou une inclination au mouvement, doit vraisemblablement estre produite par un mouvement. De sorte qu'il ne reste qu'à chercher de quelle maniere il peut agir, & dans quels corps il se peut rencontrer. A regarder simplement les corps, sans cette qualité qu'on appelle pesanteur, leurGa naar margenoot+ mouvement est naturellement ou droit ou circulaireGa naar voetnoot1). Le premier leur apartenant lors qu'ils se meuvent sans empeschement: l'autre quand ils sont retenus autour de quelque centre, ou qu'ils tournent sur leur centre mesme. Nous connoissons aucunement la nature du mouvement droit, & les loix que gardent les corps dans la communication de leurs mouvements, lorsqu'ils se rencontrent. Mais tant que l'on ne considere que cette sorte de mouvement, & les reflexions qui en arrivent entre les parties de la matiere, on ne trouve rien qui les determine à tendre vers un centre. Il faut donc venir necessairement aux proprietéz du mouvement circulaire, & voir s'il y en a quelqu'une quinous puisse servir. Je sçay que Mr. Des Cartes a aussi tasché dans sa Physique d'expliquer la pesanteur par le mouvement de certaine matiere qui tourne autour de la Terre; & c'est beaucoup d'avoir eu le premier cette penséeGa naar voetnoot1). Mais l'on verra, par les remarques que je | |
[pagina 452]
| |
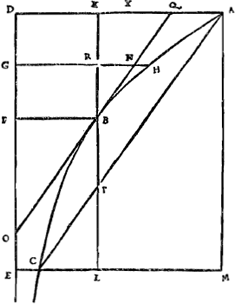
feray dans la suite de ce discours, en quoy sa maniere est differente de celle que je vais proposer, & aussi en quoy elle m'a semblé defectueuse. Il a consideré, comme moy, l'effort que font les corps, qui tournent circulairement, à s'eloigner du centre; dont l'experience ne nous permet pas de douter. Car en tournant une pierre dans une fronde, l'on sent qu'elle nous tire la main, & cela d'autant plus fort que l'on tourne plus viste; jusques là mesme que la corde peut venir à se casser. J'ay fait voir cy devant cette mesme proprieté du mouvement circulaire, en attachant des corps pesants sur une table ronde, percée au centre, & qui tournoit sur un pivot; & j'ay trouvé la determination de sa force, & plusieurs Theoremes qui la concernentGa naar voetnoot2): que l'on peut voir à la fin du livre que j'ay escrit du Mouvement desGa naar margenoot+ Pendules. Par exemple, je dis qu'un corps tournant en rond, au bout d'une | corde etendue horizontalement, s'il va avec la vitesse qu'il pourroit acquerir par sa chute, en tombant d'une hauteur egale à la moitié de la mesme corde, c'est-à-dire au quart du diametre de la circonference qu'il decrit, elle sera tirée justement avec autant de force que si elle soutenoit le mesme corps suspendu en l'airGa naar voetnoot3). L'effort à s'eloigner du centre est donc un effet constant du mouvement circulaire. & quoyque cet effet semble directement opposé à celuy de la gravité, & que l'on ait objecté à Copernic que, par le tournoiement de la terre en 24 heures, les maisons & les hommes devroient estre jettez dans l'air; je feray voir pourtant, que ce mesme effort, que font les corps tournants en rond à s'eloigner du centre, est cause que d'autres corps concourrent vers le mesme centre. 7. Imaginons nous [Fig. 129] qu'à l'entour du centre D il tourne de la matiere fluide contenue dans l'espace ABC, dont elle ne puisse point sortir à cause des autres corps qui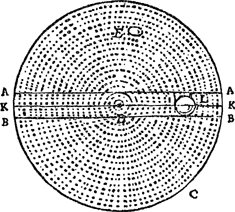 [Fig. 129]
l'environnent. Il est certain que toutes les parties de ce fluide font effort pour s'eloigner du centre D; mais sans aucun effet, puis que celles, qui devroient succeder en leur place, ont la mesme inclination à s'eloigner de ce centre. Mais si parmy les parties de cette matiere il y en avoit quelqu'une, comme F, qui ne suivist pas le mouvement circulaire des autres, ou qui allast moins vite que celles qui l'environnent;Ga naar margenoot+ je dis qu'elle sera poussée vers le centre. parce que ne faisant | point d'effort pour s'en eloigner, ou en faisant moins que les parties prochaines, elle cedera à l'effort de celles qui seront moins eloignées | |
[pagina 453]
| |
du centre D, & leur fera place en s'approchant vers ce centre, puisqu'elle ne le sçauroit faire autrement. L'on peut voir cet effet par une experience que j'ay faite expres pour celaGa naar voetnoot4), qui merite bien d'estre remarquée, parce qu'elle fait voir à l'oeil une image de la pesanteur. Je pris un vaisseau cylindrique, d'environ 8 ou 10 pouces de diametre, & dont le fond estoit blanc & uni. sa hauteur n'avoit que la moitié ou le tiers de sa largeurGa naar voetnoot5). L'ayant rempli d'eau, j'y jettay de la cire d'Espagne concasséeGa naar voetnoot6), qui, estant tant soit peu plus pesante que l'eau, va au fond; & en fuite je le couvris d'un verre, appliqué immediatement sur l'eau, que j'attachay tout autour avec du ciment, afin que rien ne pust echaper. Estant ainsi ajusté, je plaçay ce vaisseau au milieu de la table ronde, dont j'ay parlé peu devant; & la faisant tourner, je vis aussi tost que les brins de la cire d'Espagne, qui touchoient au fond, & suivoient mieux le mouvement du vaisseau que ne faisoit l'eau, s'allerent mettre tout autour des bordsGa naar voetnoot7), par la raison qu'ils avoient plus de force que l'eau à s'eloigner du centre. Mais ayant continué un peu de temps à faire tourner le vaisseau avec la table, par où l'eau acqueroit de plus en plus le mouvement circulaire, j'arrestay soudainement la table; & alors à l'instant toute la cire d'Espagne s'enfuit au centre en un monceau, qui me representa l'effet de | la pesanteur. Et laGa naar margenoot+ raison de cecy estoit que l'eau, non-obstant le repos du vaisseau, continuoit encore son mouvement circulaire, & par consequent son effort à s'eloigner du centre; au lieu que la cire d'Espagne l'avoit perdu, ou peu s'en faut, pour toucher au fond du vaisseau que estoit arresté. Je remarquay aussi que cette poudre s'alloit rendre au centre par des lignes Spirales, parce que l'eau l'entrainoit encore quelque peu. Mais si l'on ajuste, dans ce vaisseau, quelque corps en sorte, qu'il ne puisse point du tout suivre le mouvement de l'eau, mais seulement s'en aller vers le centre, il y sera alors poussé tout droit. Comme si L est une petite boule, qui puisse rouler librement sur le fond, entre les filets A A, B B & un troifiéme un peu plus élevé K K, tendus horizontalement par le milieu du vaisseau; l'on verra qu'aussi tost que le mouvement du vaisseau sera arresté, cette boule s'en ira au centre D. Et il faut noter que, dans cette derniere experience, on peut rendre le corps L de la mesme pesanteur que l'eau, & que la chose | |
[pagina 454]
| |
en succedera encore mieux; de sorte que, sans aucune difference de pesanteur des corps qui sont dans le vaisseau, le seul mouvement en produit icy l'effect. L'experience que Mr. Des Cartes propose, dans une de ses lettres impriméesGa naar voetnoot8), differe beaucoup de cellescy. car il remplit le vaisseau A B C de menuë dragée de plomb entre-meslée de quelques pieces de bois, ou d'autre matiere plus legere que le plomb: & faisant tout tourner ensemble, il dit que les pieces de bois seront chassées vers le milieu du vase. ce que je puis bien croire, pourvu toutefois qu'on frappast legerement sur les bords du vaisseau, pour faciliter la separation de ces deux matieres. Mais ce qui arrive icy n'est nullement propre à representer l'effet de la pesanteur; puis qu'on devroit conclure de cette experience, que les corps, qui contienent le moins de matiere, sont ceux qui pesent le plus. ce qui est contraire à ce qui s'observeGa naar margenoot+ dans la veritable pesanteurGa naar voetnoot9). Il propose encore, dans une autre | lettreGa naar voetnoot10), de jetter, dans de l'eau tournante, de petits morceaux de bois, & il dit qu'ils s'en iront vers le milieu de l'eau. Au quel endroit s'il entend du bois qui nage sur l'eau, comme il y a de l'apparence, il ne se fera point de concentration. Mais s'il veut qu'il aille au fond, ce sera veritablement la mesme experience que j'ay proposée peu auparavant, & le bois s'amassera au centre, mais ce sera à cause qu'en touchant au fond du vase, son mouvement circulaire sera retardé, de laquelle raison Mr. Des Cartes n'a point parlé. Or ayant trouvé dans la nature un effect semblable à celuy de la pesanteur, & dont la cause est connuë, il reste à voir si l'on peut supposer qu'il arrive quelque chose de pareil à l'égard de la Terre, c'est à dire qu'il y ait quelque mouvement de matiere qui contraigne les corps à tendre au centre, & qui s'accommode en mesme temps à tous les autres phenomenes de la pesanteur. Supposant le mouvement journalier de la Terre, & que l'air & l'ether qui l'environnent ayent ce mesme mouvement, il n'y a encore rien en cela qui doive produire la pesanteur: puisque, suivant l'experience peu devant rapportée, les corps terrestres ne devroient point suivre ce mouvement circulaire de la matiere celeste, mais estre à son égard comme en repos, s'il faloit qu'ils fussent poussez par elle vers le centre. | |
[pagina 455]
| |
Que si l'on vouloit que la matiere celeste tournast du mesme costé que la Terre, mais avec beaucoup plus de vitesse, il s'ensuivroit que ce mouvement rapide, d'une matiere qui se mouvroit continuellement & toute d'un mesme costé, se feroit sentir, & qu'elle emporteroit avec elle les corps qui sont sur la Terre; de mesme que l'eau emporte la cire d'Espagne dans nostre experience; ce qui pourtant ne se fait nullement. Mais outre cela, ce mouvement circulaire, autour de l'axe de la Terre, ne pourroit en tout cas chasser les corps, qui ne suivent pas le | mesme mouvement, que vers ceGa naar margenoot+ mesme axe, de sorte que nous ne verrions pas les corps pesants tomber perpendiculairement à l'horizon, mais par des lignes perpendiculaires à l'axe du monde, ce qui est encore contre l'experience. Pour expliquer donc la pesanteur de la maniere que je la conçoisGa naar voetnoot11), je supposeray que dans l'espace spherique, qui comprend la Terre & les corps qui sont au tour d'elle jusqu'à une grande estenduë, il y a une matiere fluide qui consiste en des parties tres petites, & qui est diversement agitée en tous sens, avec beaucoup de rapidité. Laquelle matiere ne pouvant sortir de cet espace, qui est entouré d'autres corps, je dis que son mouvement doit devenir en partie circulaire autour du centre; non pas tellement pourtant qu'elle viene à tourner toute d'un mesme sens, mais en sorte que la pluspart de ses mouvemens differens se fassent dans des surfaces spheriques à l'entour du centre dudit espace, qui pour cela devient aussi le centre de la Terre. La raison de ce mouvement circulaire est que la matiere contenue dans quelque espace, se meut plus aisement de cette maniere que par des mouvemens droits contraires les uns aux autres, lesquels mesme en se reflechissant, (parce que la matiere ne peut pas sortir de l'espace qui l'enferme) sont reduits à se changer en circulaires. L'on voit cet effect du mouvement lors qu'on essaie de l'argent par la Coupelle; car la petite boule de plomb meslée d'argent, ayant ses parties fortement agitées par la chaleur, tourne incessament autour de son centre, tantost d'un costé tantost d'un autre, changeant à tous momens, & si viste que l'oeil a de la peine à s'en appercevoir. Il arrive encore la mesme chose à une goute de suif de chandelle, lors que la tenant suspendue à la pointe des mouchettes, on l'approche de la flame, car elle se met à tourner avec une tres grande vitesse. Il est vray que d'ordinaire cette goute tourne toute d'un | costé ou d'autre, selonGa naar margenoot+ que la flame de la chandelle vient à la toucher. Mais dans la matiere celeste, que j'ay supposée, il n'en doit pas arriver de mesme, par ce qu'ayant une fois du mouvement en tous sens, il faut qu'il en demeure tousjours, quoyqu'il soit changé en spherique, par ce qu'il n'y a pas de raison pourquoy le mouvement d'une partie de la matiere | |
[pagina 456]
| |
l'emporteroit sur celuy des autres, pour faire que toute la masse tournast d'un mesme sens. Car au contraire, la loy de la nature, que j'ay rapportée ailleurs, est telle dans la rencontre des corps qui sont diversement agitez, qu'il s'y conserve tousjours la mesme quantité de mouvement vers le mesme costé. Et quoy que ces mouvemens circulaires, en tant de sens divers dans un mesme espace, semblent se devoir contrarier & empescher souvent; la grande mobilité toute fois de la matiere, aydée par la petitesse de ses parties, qui surpasse de beaucoup l'imagination, fait qu'elle souffre assez facilement toutes ces differentes agitations. L'on voit quand on a brouillé de l'eau dans une phiole de verre, de combien de differens mouvemens ses parties sont capables; & il faut se figurer la liquidité de la matiere celeste incomparablement plus grande que celle que nous remarquons dans l'eau, qui estant composée de parties pesantes, entassées les unes sur les autres, devient par là paresseuse au mouvement; au lieu que la matiere celeste, se mouvant librement de tous costez, prend tres facilement des impressions differentes par les diverses rencontres de ses parties, ou par la moindre impulsion des autres corps. & s'il n'estoit ainsi, l'air ne cederoit pas si facilement qu'il fait au mouvement de nos mains. De sorte qu'il faut considerer que les mouvemens circulaires de cette matiere fluide, autour de la Terre, sont bien souvent interrompus & changez en d'autres, mais qu'il en demeure tousjours plus que de ceux qui suivent d'autres routes: ce qui suffit pour le present dessein. Ga naar margenoot+ Il n'est pas difficile maintenant d'expliquer comment par ce mouvement la pesanteur est produite. Car si parmy la matiere fluide, qui tourne dans l'espace que nous avons supposé, il se rencontre des parties beaucoup plus grosses que celles qui la composent, ou des corps saits d'un amas de petites parties accrochées ensemble, & que ces corps ne suivent pas le mouvement rapide de ladite matiere, ils seront necessairement poussez vers le centre du mouvement, & y formeront le globe Terrestre s'il y en a assez pour cela, supposé que la Terre ne fust pas encore. Et la raison est la mesme que celle qui, dans l'experience raportée cy dessus, fait que la cire d'Espagne s'amasse au centre du vaisseau. C'est donc en cela que consiste vraisemblablement la pesanteur des corps: laquelle on peut dire, que c'est l'effort que fait la matiere fluide, qui tourne circulairement autour du centre de la Terre en tous sens, à s'éloigner de ce centre, & à pousser en sa place les corps qui ne suivent pas ce mouvement. Or la raison pourquoy des corps pesants, que nous voions descendre dans l'air, ne suivent pas le mouvement spherique de la matiere fluide, est essez manifeste; parce qu'y ayant de ce mouvement vers tous les costez, les impulsions qu'un corps en reçoit se succedent si subitement les unes aux autres, qu'il y intercede moins de temps qu'il luy en faudroit pour acquerir un mouvement sensible. Mais comme cette seule raison ne suffit pas pour empêcher que les corps les plus menus que l'oeil puisse appercevoir, comme sont les brins de poussiere qui voltigent dans l'air, ne soient point chassez ça & là par la rapidité de ce mouvement; il faut sçavoir que ces petits corps ne nagent pas dans la seule matiere liquide qui cause la pesanteur: mais qu'outre celle cy il y a d'autres matieres, composées de particules plus grossieres, qui remplissent la plus | |
[pagina 457]
| |
grande partie de l'espace qui est autour de nous, & mesme ceux des | cieux; lesquellesGa naar margenoot+ particules quoyque differemment agitées & reflechies entre elles, ne suivent pas le mouvement soudain de la matiere liquide; parce qu'estant contiguës, ou peu distantes les unes des autres, une trop grande quantité devroit se mouvoir à la fois. L'on sçait qu'il y a autour de la Terre premierement les particules de l'air, lesquelles on fera voir tout à l'heure estre plus grossieres que celles de la matiere fluide que nous avons supposée. Je dis de plusGa naar voetnoot12) qu'il y a une matiere dont les particules sont plus menuës que celles de l'air, mais plus grossieres que celles de cette matiere fluide: ce qui se prouve par nostre experience, qu'on fait avec la Machine qui vuide l'air. Où l'on remarque l'effet d'une matiere invisible qui pese là où il n'y a point d'air; puis qu'elle y soutient l'eau suspendue dans un tube de verre, dont le bout ouvert est plongé dans d'autre eau: & qu'elle y sait couler l'eau d'un siphon recourbé, de mesme que dans l'air: pourvu que l'eau, dans ces experiences, ait esté purgée d'air; ce qui se fait en la laissant pendant quelques heures dans le vuide. Il paroit par là premierement, que les particules, de ce corps pesant & invisible, sont plus petites que celles de l'air, puisqu'elles passent à travers le verre qui exclud l'air, & qu'elles y font apercevoir leur pesanteur. Il paroit de plus qu'elles doivent estre plus grossieres que les particules de la matiere fluide qui cause la pesanteur, afin que le corps qu'elles composent ne suive pas le mouvement de cette matiere, par ce qu'en le suivant il ne seroit pas pesant. Il peut y avoir autour de nous encore d'autres sortes de matieres de differents degrez de tenuité, quoyque toutes plus grossieres que n'est la matiere qui cause la pesanteur. Lesquelles contribueront donc toutes à empêcher les petits brins de la poussiere d'estre emportez par le mouvement rapide de cette matiere, parce qu'elles ne suivent pas ce mouvement elles mesmesGa naar voetnoot13). Il ne faut pas au reste trouver etranges ces differents degrez | de petits corpuscules,Ga naar margenoot+ ni leur extreme petitesse. Car bien que nous ayons quelque penchant à croire que des corps, à peine visibles, sont desja presque aussi petits qu'ils le peuvent estre, la raison nous dit que la mesme proportion qu'il y a d'une montagne à un grain de sable, ce grain la peut avoir à un autre petit corps, & cettuicy encore à un autre, & cela autant de fois qu'on voudra. L'extreme petitesse des parties de nostre matiere fluide est encore d'une necessité absolue pour rendre raison d'un effet considerable de la pesanteur; qui est que des corps pesants, enfermez de tous costez dans un vaisseau de verre, de metail, ou de | |
[pagina 458]
| |
quelqu'autre matiere que ce soit, se trouvent peser tousjours egalement. De sorte qu'il faut que la matiere que nous avons dit estre cause de la pesanteur, passe tres librement à travers tous les corps qu'on estime les plus solides, & avec la mesme facilité qu'à travers l'air. Ce qui se confirme encore par ce que, s'il n'y avoit pas cette liberté de passage, une bouteille de verre peseroit autant qu'un corps massif de verre de la mesme grandeur; & que tous les corps solides d'egal volume peseroient egalement; puisque, selon nostre Theorie, la pesanteur de chaque corps est reglée par la quantité de la matiere fluide qui doit monter en sa place. Cette matiere passe donc facilement dans les interstices des particules dont les corps sont composez, mais non pas par les particules mesmes; & ce qui cause les diverses pesanteurs, par exemple, des pierres, des metaux &c. c'est que ceux de ces corps, qui sont plus pesants, contienent plus de telles particules, non en nombre mais en volumeGa naar voetnoot14): car c'est en leur place seulement que la matiere fluide peut monter. Mais parce qu'on pourroit douter, si ces particules, estant impenetrables à la dite matiere,Ga naar margenoot+ sont pour cela entierement solides: (car ne l'estant pas, ou mes|me estant vuides, elles devroient faire le mesme effet, par la raison que je viens de dire) je demontreray qu'elles ont cette parfaite solidité; & que par consequent la pesanteur des corps suit precisement la proportion de la matiere, qui les compose. Je feray remarquer pour cela ce qui arrive dans le choc de deux corps, quand ils se rencontrent d'un mouvement horizontal. Il est certain que la resistence que font les corps à estre mûs horizontalement, comme seroit une boule de marbre ou de plomb posée sur une table bien unie, n'est pas causée par leur poids vers la Terre, puisque le mouvement lateral ne tend pas à les eloigner de la Terre, & qu'ainsi il n'est nullement contraire à l'action de la pesanteur, qui les pousse en bas. Il n'y a donc rien que la quantité de matiere attachée ensemble, que chaque corps contient, qui produit cette resistence: de sorte que si deux corps en contienent autant l'un que l'autre, ils reflechiront egalement, ou demeureront tous deux sans mouvement, selon qu'ils seront durs ou mols. Mais l'experience fait voir que toutes les fois que deux corps reflechissent ainsi egalement ou s'arrestent l'un l'autre, estant venus à se rencontrer avec d'egales vitesses, ces corps sont d'egale pesanteur: donc il s'ensuit que ceux, qui sont composez d'egale quantité de matiere, sont aussi d'egale pesanteur. ce qu'il faloit demonstrer. | |
[pagina 459]
| |
Mons. Des Cartes estoit en cecy d'un autre sentiment, comme encore en ce qui regarde le passage libre de la matiere, qui cause la pesanteur, à travers les corps sur lesquels elle agit. Car pour ce qui est de ce dernier point, il veut que cette matiere soit empechée, par la rencontre de la Terre, de continuer ses mouvements en ligne droite, & que pour cela elle s'en eloigne le plus qu'elle peut. En quoy il semble n'avoir pas pensé à cette proprieté de la pesanteur que j'ay fait remarquer peu aupa|ravant.Ga naar margenoot+ Car si le mouvement de cette matiere est empêché par la Terre, elle ne penetrera non plus librement les corps des metaux ni celuy du verre. D'où il s'ensuivroit que du plomb enfermé dans une phiole perdroit son poids à l'égard de la phiole mesme, ou que du moins ce poids seroit diminué. De plus, en portant un corps pesant au fond d'un puits, ou dans quelque carriere ou mine profonde, il y devroit perdre beaucoup de sa pesanteur. Mais on n'a pas trouvé, que je scache, par experience qu'il en perde quoy que ce soit. Quant à l'autre point, Mr. Des Cartes pretend, que, quoy qu'une masse d'or soit vingt fois plus pesante qu'une portion d'eau de la mesme grandeur, l'or neanmoins peut ne contenir que 4 ou 5 fois autant de matiere que l'eau: premierement à cause qu'il faut deduire (il faloit plutost dire adjouter) un poids égal à l'un & l'autre, à raison de l'air dans lequel on les pese: & puis parce que l'eau & les autres liquides ont quelque legereté à l'egard des corps durs, d'autant que les parties des premiers sont en un mouvement continuel. Mais on peut respondre à la premiere de ces deux raisons, que la pesanteur de l'air autour de nous, n'estant à celle de l'eau qu'environ comme 1 à 800, ce ne sera pas un poids considerable qu'il faudra adjouter également à celuy de l'eau & de l'or, trouvé par la balance. Et pour l'autre raison, si elle estoit bonne, il faudroit qu'une mesme portion d'eau, apres estre gelée pesast bien d'avantage qu'estant liquide; & de mesme les metaux en masse, plus que quand ils sont fondus; ce qui est contre l'experience. Outre que je ne vois pas comment il a conceu que le mouvement des parties des corps liquides leur donneroit de la legereté, c'est-à-dire de l'effort pour s'ecarter du centre, puisque pour cela il faudroit que ce mouvement fust circulaire autour du centre de la Terre, ou qu'il fust plus fort vers le haut que vers le bas, ce qu'il n'a jamais dit, mais bien | au contraire que les parties des liqueurs se meuvent en tous sens indifferemment.Ga naar margenoot+ Il ne semble non plus avoir consideré combien la vitesse de la matiere fluide doit estre grande, pour donner autant de pesanteur qu'on en trouve à la plus part des corps: parce qu'autrement il auroit bien jugé que le mouvement, que peuvent avoir les parties de l'eau & de semblables liquides, n'est nullement comparable au mouvement de cette matiere qui cause la pesanteur. Pour moy j'ay recherché soigneusement le degré de cette vitesse, & je crois pouvoir determiner à peu prés à combien elle doit monter. Et puis que plusieurs autres effets naturels en peuvent dependre, il ne sera pas inutile de faire voir icy ce que produit mon calcul, & sur quoy il est fondé. Reprenant donc la figure dont je me suis servi cy | |
[pagina 460]
| |
dessus, puis que la pesanteur du corps E est justement égale à l'effort avec lequel une portion aussi grande, de la matiere fluide, tend à s'éloigner du centre D; ou que c'est
 [Fig. 129].
plutost la mesme chose; il faut qu'une livre de plomb, par exemple, pese autant vers la Terre, qu'une masse de la matiere fluide, de la grandeur de ce plomb, (j'entens de la grandeur que font ses parties solides) pese du costé d'enhaut pour s'éloigner du centre, par la vertu de son mouvement circulaire. Or la matiere du plomb & la matiere fluide ne different en rien selon nostre hypothese. On peut doncGa naar margenoot+ dire que la livre de | plomb pese autant vers le bas, qu'elle peseroit vers le haut, si, demeurant à la mesme distance du centre de la Terre, elle tournoit autour avec autant de vitesse que fait la matiere fluide. Mais je trouve par ma Theorie du mouvement Circulaire, qui s'accorde parfaitement avec l'experience, qu'un corps tournant en cercle, si on veut que son effort à s'éloigner du centre, égale justement l'effort de sa simple pesanteur, il faut qu'il fasse chaque tour en autant de temps, qu'un Pendule, de la longueur du demi diametre de ce cercle, en emploie à faire deux allées. Il faut donc voir en combien de temps un pendule, de la longueur du demidiametre de la Terre, feroit ces deux allées. Ce qui est aisé par la proprieté connue des pendules, & par la longueur de celuy qui bat les Secondes, qui est de 3 pieds 8½ lignes, mesure de Paris. Et je trouve qu'il faudroit pour ces deux vibrations 1 heure 24½ minutes; en supposant, suivant l'exacte dimension de Mr. Picard, le demidiametre de la Terre de 19615800 pieds de la mesme mesureGa naar voetnoot15). La vitesse donc de la matiere fluide, à l'endroit de la surface de la Terre, doit estre égale à celle d'un corps qui feroit le tour de la Terre dans ce temps de 1 heure, 24½Ga naar voetnoot16) minutes. Laquelle vitesse est, à fort peu pres, 17 fois plus grande que celle d'un point sous l'Equateur; qui fait le mesme tour, à l'égard des Etoiles fixes, comme on doit le prendre icy, en 23 heures, 56 minutes. ce qui paroit par la proportion entre ce temps & celuy d'une heure 24½ minutes, qui est tres pres comme de 17 à 1. | |
[pagina 461]
| |
Je sçay que cette rapidité semblera étrange à qui la voudra comparer avec les mouvemens qui se voient icy parmy nous. Mais cela ne doit point faire de difficulté; & mesme, par raport à sa sphere, ou à la grandeur de la Terre, elle ne paroitra point extraordinaire. Car si, par exemple, en regardant un Globe Terrestre, de ceux qu'on fait pour l'usage de la Geogra|phie, on s'imagine sur ce globe un point qui n'avanceGa naar margenoot+ que d'un degré en 14 Secondes ou battemens de pous, qui est la vitesse de la matiere que je viens de dire; on trouvera ce mouvement tres mediocre, & mesme il pourra sembler estre lentGa naar voetnoot17). Il y a au reste plusieurs effets naturels qui semblent demander une matiere extremement agitée, & qui penetre facilement par les pores des corps. Telle est la force de la poudre à Canon, qui en s'allumant ne prend pas son mouvement violent d'elle mesme, ni de celuy qui en aproche la mesche; & par consequent il faut qu'il viene de quelqu'autre matiere qui ait ce mouvement, & qui se trouve par tout; faisant son effet toutes les fois qu'elle y trouve une disposition convenable. Telle est aussi, à ce que je conçois, la force du Ressort, tant de l'acier & autres corps solides, que de celuy de l'air. A quoy l'on peut joindre celle des muscles des animaux: qu'on explique fort bien par une fermentation que le suc des nerfs cause dans le sang: mais d'où viendra la force de la fermentation, si ce n'est de quelque mouvement de dehors? La puissante action de la Gelée ne paroit pas non plus concevable, si on n'a recours à une impulsion violente de quelque matiere, qui fasse étendre ou la glace, en y introduisant d'autres particules, ou les bulles qui s'y forment, en augmentant l'air qu'elles contienent. Ce qui se fait avec tant de violence, que j'en ay vû crever des canons de mousquet, dans lesquels l'eau avoit esté enfermée. Mais pour revenir à la Pesanteur; l'extreme vitesse de la matiere qui la cause, sert encore à expliquer comment les corps pesants, en tombant, accelerent tousjours leur mouvement, quand mesme ils l'ont desja acquis à un fort grand degré de vitesse. Car celuy de la matiere fluide, surpassant encore de beaucoup la celerité d'un boulet de canon, par exemple, qui retombe de l'air, apres y avoir esté tiré perpendiculairement; ce boulet, jusqu'à la fin de sa chûte, ressent à fort peu prés la mesme | pression de cetteGa naar margenoot+ matiere, & partant sa celerité en est continuellement augmentée. Au lieu que, si la matiere n'avoit qu'un mouvement mediocre, la balle apres en avoir acquis autant, n'accelereroit plus sa chûte, par ce qu'autrement elle seroit obligée de pousser cette mesme matiere, à succeder dans sa place avec plus de vitesse qu'elle n'auroit pour cela par son propre mouvement. L'on peut enfin trouver icy la raison du Principe que Galilée a pris pour demontrer la proportion de l'acceleration des corps qui tombent; qui est que leur vitesse s'augmente egalement en des temps egaux. Car les corps estant poussez successivement | |
[pagina 462]
| |
par les parties de la matiere qui tasche de monter en leur place, & qui, comme on vient de voir, agissent continuellement sur eux avec la mesme force, du moins dans les chûtes qui tombent sous nostre experience; c'en est une suite necessaire que l'accroissement des vitesses soit proportionel à celuy des temps. Ainsi donc j'ay expliqué, par une Hypothese qui n'a rien d'impossiible, pourquoy les corps terrestres tendent au centre; pourquoy l'action de la gravité ne peut estre empêchée par l'interposition d'aucun corps de ceux que nous connoissons; pourquoy les parties de dedans de chaque corps contribuent toutes à sa pesanteur; & pourquoy en fin les corps en tombant augmentent continuellement leur vitesse, & cela dans la raison des temps. Qui sont les proprietez de la pesanteur qu'on avoir remarquées jusqu'a presentGa naar voetnoot18). Il en reste une encore, que jusqu'icy on n'a pas crû moins certaine; qui est que les corps pesans le sont autant en un endroit de la Terre qu'en un autre. Ce qui aiant esté trouvé autrement, par des observations qu'on a faites depuis peu, il vaut la peine d'examiner d'où cela peut proceder, & quelles en sont les consequences. Ga naar margenoot+ L'on assure d'avoir trouvé dans la Caiene, qui est un païs | dans l'Amerique, eloigné seulement de 4 ou 5 degrez de l'Equateur, qu'un Pendule qui bat les Secondes, y est plus court qu'a Paris d'une ligne & un quart. d'où sensuit que, si on prend des pendules d'égale longueur, celuy de la Caiene fait des allées un peu plus lentes que celuy de Paris. La verité du fait estant posée, on ne peut douter que ce ne soit une marque assurée de ce que les corps pesans descendent plus lentement en ce païs là qu'en France. Et comme cette diversité ne sçauroit estre attribuée à la tenuité de l'air, qui est plus grande dans la zone Torride; parce qu'elle devroit causer un effet tout contraire; je ne vois pas qu'il puisse y avoir d'autre raison, sinon qu'un mesme corps pese moins sous la ligne que sous des Climats qui s'en éloignent. Je reconnus, aussi tost qu'on nous eust communiqué ce nouveau phenomene, que la cause en pouvoit estre raportée au mouvement journalier de la Terre: qui estant plus grand en chaque païs, selon qu'il approche plus de la ligne Equinoctiale, doit produire un effort proportionné à rejetter les corps du centre; & leur oster par là une certaine partie de leur pesanteur. Et il est aisé, par les choses expliquées cy dessus, de sçavoir la quantieme partie ce doit estre, dans les corps qui se trouvent placez sous l'Equateur. Car ayant trouvé, comme on a vû, que, si la Terre tournoit 17 fois plus viste qu'elle ne fait, la force Centrifuge sous l'Equateur seroit égale à toute la pesanteur d'un corps: il faut que le mouvement de la Terre, tel qu'il est maintenant, oste une partie de la pesanteur, qui soit à la pesanteur entiere comme 1 au quarré de 17, c'est-à-dire 1/289; parce que les forces des corps, à s'éloigner du centre autour du quel ils tournent, sont entre elles comme les quarrez de leurs vitesses, suivant mon Theoreme 3e de Vi Centrifuga. | |
[pagina 463]
| |
Chaque corps, sous l'Equateur, estant donc moins pesant de 1/289 de ce qu'il seroit si la Terre ne tournoit point sur son axe; il s'ensuit, par les loix de la Mechanique, que la longueur | d'un Pendule, en cet endroit, doit aussi estre diminuée de 1/289, pour faireGa naar margenoot+ ses allées dans le mesme tems qu'il les feroit sur la Terre immobile. Mais pour sçavoir la diminution que doit souffrir un Pendule, qui de Paris est transporté sous la ligne Equinoctiale, il faut considerer qu'a Paris sa longueur est desia moindre que si la Terre estoit en repos; parce que le mouvement journalier fait aussi sous ce parallele son effort à éloigner les corps du centre de la Terre. Lequel effort n'est pourtant pas si grand qu'il est sous la Ligne; tant à cause que le cercle du mouvement est moindre, que parce qu'il ne chasse pas les corps directement en haut, mais suivant la perpendiculaire à l'axe de la Terre, comme l'on verra par cette figure. Le cercle P A Q E [Fig. 130] y represente la Terre, coupée par un plan qui passe par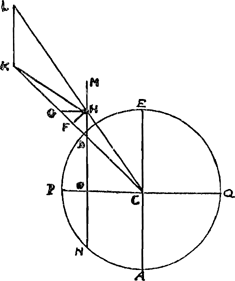 [Fig. 130]
ses deux poles, P, Q. le centre est C: le cercle Equinoctial E C A: le parallele de Paris D O N, supposant que Paris est en D. K H represente une corde qui soutient un plomb H, qui s'écarte de la perpendiculaire K D C, parce qu'il est rejetté, par le mouvement circulaire, suivant la ligne O D M; que je suppose passer par le poids H. Pour connoitre maintenant quelle doit estre la situation du fil K H, & combien moins le plomb H pese de cette façon, que s'il pendoit perpendiculairement le | long de K D;Ga naar margenoot+ il faut considerer le point H comme estant tiré par trois fils, H C, HM, H K. desquels H C le tire vers le centre de la Terre, avec tout le poids que le plomb auroit si la Terre estoit sans mouvement. mais H M le tire de son costé avec la force que donne le mouvement de la Terre dans le cercle D N. & le troisieme fil H K tire, ou est tiré, avec une force qui est celle qu'on cherche. Ayant donc prolongé C H, & mené K L parallele à D M; l'on sçait que les trois costez du triangle H L K sont proportionels aux puissances qui tirent le point H: le costé L H respondant à celle qui tire par H C; le costé K L à celle qui tire par H M; & le costé H K à la puissance qui tire ou soutient le plomb par le fil K H. Mais le triangle K D H est censé avoir tous ses costez egaux à ceux du triangle H L K, parce que C H L est comme parallele à C D K. Les costez donc de K D H respondent aux mesmes puissances: sçavoir le costé K D à la pesanteur absoluë du poids H, qu'il auroit si la Terre ne tournoit point; D H à la puissance que luy imprime le mouvement journalier; & K H à la pesanteur qu'on cherche. Or ce triangle K H D est donné. car puis que nous sçavons que l'effort circulaire, sous l'Equateur en E, est 1/289 du poids absolu: & puisque cet effort est à celuy en D, ou en H, comme E C à D O, qui sont en raison | |
[pagina 464]
| |
Ga naar margenoot+ donnée, nous sçau | rons donc aussi, quelle partie du poids absolu est l'effort centrifuge en D ou H. c'est-à-dire que la raison de D K à D H sera connue, comme estant composée de celle de 289 à 1, & de E C à D O. Mais l'angle H D K est aussi connu, estant égal à celuy de la Latitude de Paris, sçavoir de 48 degr. 51 min. Donc on connoitra la raison de D K à K H, qui est celle de la pesanteur absoluë des corps, à celle qu'ils ont à Paris, & qui est encore celle de la longueur du pendule sur la Terre immobile, à la longueur qu'il doit avoir sous ce Parallele, suivant ce qui desia a esté dit. Et puis que la longueur du pendule à Secondes est donnée à Paris, l'on sçaura aussi celle qu'auroit le pendule à Secondes sur la Terre immobile, & quelle est leur difference, & de combien cette difference est moindre que cette 1/289, que nous avions trouvée sous l'Equateur. Pour faire cette supputation avec facilité, & sans le calcul des triangles, il faut sçavoir, & nous le prouverons à cette heure, que, comme le quarré du rayon E C est au quarré de D O, sinus du complement de la Latitude de Paris, ainsi est 1/289, difference ou racourcissement du pendule sous l'Equateur, à la difference ou racourcissement à Paris. Qui se trouve par la estre 1/668 de la longueur du pendule sur la Terre immobile, ou sous le Pole. Et puisque le Pendule à secondes à Paris, est de 3 pieds 8½ lignes; il s'ensuit que la Longueur du pendule sur la Terre immobile, ou sous le Pole, seroit de 3 pieds 9 ⅙ lignes. d'où ostant 1/289, qui fait 1 ½ ligne, on aura la longueur du pendule à Secondes, sous l'Equateur, de 3 pieds 7½ lignes. De sorte que ce pendule seroit plus court, que celuy de Paris, de ⅚ d'une ligne; qui est un peu moins que ce qui a esté trouvé à la Caiene par Mr. Richer, sçavoir une ligne & un quart. Mais on ne peut pas se sier entierement à ces premieres observations, desquelles on ne voit marqué aucune circonstance. Et encore moins, à ce que je crois, à cellesGa naar margenoot+ qu'on dit avoir | esté faites à la Gadaloupe, où le racourcissement du pendule de Paris auroit esté trouvé de 2 lignesGa naar voetnoot19). Il faut esperer qu'avec le temps nous serons informez au juste de ces differentes longueurs, tant sous la ligne qu'en d'autres Climats; & certainement la chose merite bien d'estre recherchée avec soin, quand ce ne seroit que pour corriger, suivant cette Theorie, les mouvemens des Horloges à Pendule, en les faisant servir à mesurer les Longitudes sur mer. Car une Horloge, par exemple qui seroit bien reglée à Paris, estant transportée en quelque endroit sous l'Equateur, retarderoit environ d'une minute & 5 secondes en 24 heures; comme il est aisé de supputer suivant le raisonnement precedent: & ainsi à proportion pour chaque different | |
[pagina 465]
| |
degré de Latitude. Où l'on trouvera que ces retardemens, entre eux, suivent assez precisément la mesme proportion que les diminutions de la longueur du pendule: &
 [Fig. 130]
que le plus grand retardement, tel que seroit celuy d'une Horloge sous l'Equateur, lors qu'elle auroit esté reglée sous le Pole, seroit par jour fort prés de 2½ minutes. En ayant donc calculé des Tables, on pourroit corriger, par leur moien, le mouvement des Horloges, & s'en servir avec la mesme sureté que si ce mouvement estoit par tout égal. Pour demonstrer ce qui a esté posé un peu auparavant, en | cherchant la diminution duGa naar margenoot+ Pendule à Paris, (& c'est la mesme chose dans quelque autre lieu que ce soit) lorsqu'on connoit la quantité de cette diminution sous l'Equateur: soit prise, dans la mesme figure, K F égale à K H, & soit H G parallele à l'axe P Q. Il a esté montré que H D est à D K, comme l'effort à s'éloigner du centre, en D ou H, au poids absolu fur la Terre immobile. Mais comme E C ou C D à D O, c'est à-dire comme G D à H D, ainsi est l'effort centrifuge en E, sous l'Equateur, à celuy en D. Donc comme G D à D K, ainsi sera l'effort centrisuge en E, au poids absolu sur la Terre immobile. Et la ligne G D sera le racourcissemenr du pendule, qui est requis sous l'Equateur, suivant ce qui a esté dit cy devant. Mais F D est le racourcissement à Paris; & G D est à D F comme le quarré de G D au quarré de D H; parce que la petitesse de l'angle D K H, fait que H F peut estre considerée comme perpendiculaire à G D. Le racourcissement donc sous l'Equateur, à celuy qui convient à Paris, est comme le quarré de G D au quarré de D H; c'est-à-dire comme le quarré de C D, ou de E C, au quarré de D O. ce qu'il faloit demontrer. Il reste à considerer l'angle H K D, dans la mesme figure; qui marque de combien le plomb K H, estant en repos, decline de la perpendiculaire K D. Où je trouve que, sous le Parallele de Paris, cet angle est de 5 minutes 54 secondes; & qu'il doit estre encore un peu plus grand au 45e degré de Latitude. Cette declinaison est bien contraire à ce qu'on a supposé, de tout temps, comme une verité tres certaine; sçavoir que la corde, qui tient un plomb suspendu, tend directement au centre de la Terre. Et cet angle, d'une dixieme de degré, est assez considerable, pour faire croire qu'on devroit s'en estre aperceu, soit dans les observations Astronomiques, soit dans celles qu'on fait avec le Niveau. Car pour ne parler que de ces dernieres, | ne faudroit il pas, qu'en regardant du costé du Nort, la ligne du niveauGa naar margenoot+ baissast visiblement sous l'Horizon? ce qui pourtant n'a jamais esté remarqué, ni qui assurément n'arrive point. Et pour en dire la raison, qui est un autre paradoxe, c'est | |
[pagina 466]
| |
que la Terre n'est pas tout à fait spherique, mais d'une figure de sphere abaissée vers les deux Poles, telle que feroit à peu prés une Ellipse, en tournant sur son petit axe. Cela procede du mouvement journalier de la Terre, & c'est une suite necessaire de la declinaison susdite du plomb. Parce que la descente des corps pesans estant parallele à la ligne de cette suspension, il faut que la surface de tout liquide se dispose en sorte, que cette ligne luy soit perpendiculaire, parce qu'autrement il pourroit descendre d'avantageGa naar voetnoot20). Partant la surface de la mer est telle, qu'en tout lieu le fil suspendu luy est perpendiculaire. D'ou s'ensuit que la ligne du niveau, c'est-à-dire celle qui coupe le fil, du plomb suspendu, à angles droits, doit marquer l'horizon, ainsi qu'elle fait; n'y ayant que la hauteur du lieu, où le niveau est placé, qui le fasse viser quelque peu plus haut. Or les costes des terres estant generalement elevées, & presque par tout de mesme, à l'egard de la mer; il s'ensuit que tout le composé, de terres & de mers, est reduit a la mesme figure spheroïde que la surface de la mer se donne necessairement. Et il est à croire, que la Terre a pris cette figure, lors qu'elle a esté assemblée par l'effect de la pesanteurGa naar voetnoot21): sa matiere ayant dés lors le mouvement circulaire de 24 heures. | |
Addition.Quelque temps aprés que j'eus achevé d'escrire ce qui precede, ayant receu & examiné le journal du voiage, qui, par ordre de Messieurs les Directeurs de la CompagnieGa naar margenoot+ des Indes Orientales, a esté fait, avec nos Horloges à pendule, | jusqu'au Cap de Bonne Esperance; & du depuis ayant encore lû le tres sçavant ouvrage de Mr. Newton, dont le titre est Philosophiae Naturalis principia MathematicaGa naar voetnoot22); l'un & l'autre me fournit de la matiere pour étendre d'avantage ce Discours. Et premierement, quant aux differentes longueurs des Pendules dans divers Climats, dont il a aussi traité, je crois avoir, par le moien de ces Horloges, non seulement une confirmation évidente de cet effect du mouvement de la Terre, mais aussi de la mesure de ces longueurs, qui s'accorde tres bien avec le calcul que je viens d'en donner. Car ayant corrigé & rectifié, suivant ce calcul, les Longitudes qu'on avoit mesurées par les Horloges, au retour du Cap de B. Espe. jusqu'au Texel en Hollande, (car en allant elles n'avoient point servi) j'ay trouvé que la route du vaisseau en estoit beaucoup mieux | |
[pagina 467]
| |
marquée sur la Carte, qu'elle n'estoit sans cette correction; & si bien, qu'en arrivant à ce Port, il n'y avoit pas 5 ou 6 lieues d'erreur dans la Longitude ainsi rectifiée. Supposant que celle dudit Cap avoit esté bien prise par les P.P. Jesuites, lors qu'ils y passerent en l'année 1685, en allant à Siam; & qu'elle est de 18 degrez plus à l'Est que celle de Paris; ce que je sçay encore d'ailleurs ne s'éloigner guere de la veritéGa naar voetnoot23). Le detail de toute cette affaire est deduit au long dans le Raport que j'ay fait, touchant ce voiage des Pendules, aux dits Messieurs les Directeurs. Sur lequel raport, apres l'avoir fait examiner par des personnes intelligentes, il leur a plû d'ordonner qu'on fist une seconde epreuve; pour s'assurer par plusieurs experiences de la bonté de cette invention. L'on verra quel sera le succés de cet autre voiage, & particulierement en ce qui est de la variation des Pendules. estant certain que, pour la bien connoitre, ces Horloges donnent un moyen plus seur, par leur acceleration & retardement, que n'est celuy de mesurer actuellement la longueur du pendule à Secondes en differens païs. Cependant, parce | que dans l'essay, dont je viens de parler, l'experienceGa naar margenoot+ s'est si bien accordée avec ce que j'avois trouvé par raisonnement, je m'y fie assez pour vouloir continuer cette speculation, en cherchant premierement, quelle est donc la forme de la Terre, puisque, comme il a esté dit, elle n'est pas Spherique. Il est bon pour cela de la considerer comme toute couverte d'eau, ou comme si toute sa masse n'estoit autre chose. Et alors il paroit, par ce qui a esté expliqué cy dessus, que la surface doit estre telle, que, dans quelque endroit que ce soit, le fil, qui soutient un plomb, l'aille rencontrer à angles droits; ayant égard à la pesanteur ensemble, & à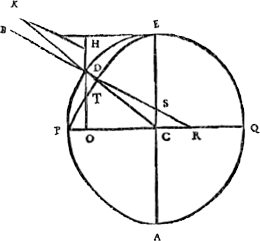 [Fig. 131]
la force centrifuge, qui detourne le fil de sa direction vers le centre. Parce que si le fil ne rencontroit pas la surface à angles droits, elle ne pourroit pas demeurer en l'assiete où elle est. Supposé donc les mesmes choses, que dans la derniere figure du discours precedent, & aussi ce qui en a esté expliqué; mais faisant la forme de la Terre un peu diminuée & applatie vers les Poles, en sorte que l'axe P Q [Fig. 131] soit plus court que le diametre E A; soit menée B D S R parallele à K H, coupant E A, P Q en S & R. Puisque le fil K H, qui soutient le plomb, ou plutost sa parallele B D, doit rencontrer | |
[pagina 468]
| |
la surface de la mer à angles droits; & puisque ce fil pend en sorte, que K D est à D H,Ga naar margenoot+ ou D C à | C S, comme la pesanteur absoluë à la force centrifuge en D; laquelle raison est composée de celle de la pesanteur absoluë, à la force centrifuge en E, qui est comme de 289 à 1, & de celle de cette force à la force centrifuge en D, qui est comme E C à D O; il paroit que la nature de la Ligne courbe E D P est determinée par la proprieté de sa perpendiculaire, comme D R; c'est-à-dire qu'en menant une telle perpendiculaire, tousjours la raison de D C à C S doit estre composée d'une raison donnée, & de celle de E C à D O. Ou bien, comme on en peut inferer facilement, que la raison de D O à C S, ou de O R à R C doit estre composée de la dite raison donnée, & de celle de E C à C D. Or il est difficile de trouver ainsi des lignes courbes par la proprieté donnée de leurs perpendiculaires, ou, ce qui est la mesme chose, par la proprieté de leur TangentesGa naar voetnoot24). Mais il y a un moyen assez aisé pour cette courbe icy, qui est fondé sur l'equilibre de certains canaux, dont Mr. Newton a donné la premiere idée. Le canal qu'il suppose est representé dans nostre figure par E C P, faisant un angle droit au centre de la Terre. Il faut le concevoir comme ayant quelque peu de creux, & rempli d'eau. Ce qui estant, il est certain que les deux jambes, E C, C P, se doivent tenir en équilibre, si l'on suppose que la Terre, estant toute composée d'eau, prend une figure, dont les diametres soient E A & P Q: parce qu'autrement, cette eau du canal, ne demeureroit pas non plus dans son assiete en la concevant sans canal, contre ce qu'on suppose. d'où il est aisé de trouver la raison de E A à P Q. Car en posant E C ∞ a; C P ∞ b, & representant la pesanteur absoluë par une ligne p; & la force centrifuge en E par la ligne n; le poids du canal P C est p b, sçavoir ce qui se fait en multipliant toutes les parties de ce canal egalement par la ligne p. Mais le poids duGa naar margenoot+ canal E C, qui seroit | p a, est diminué par la force centrifuge de toutes ses parties, des quelles la plus élevée, qui est en E, a la force n; & toutes les autres parties l'ont proportionée à celle cy, suivant leur distances du centre D. ce qui fait ½ na pour toute la force centrifuge de l'eau du canal E C, qui estant ostée de son poids p a, reste p a-½ n a; qui doit estre égal à p b poids du canal P C. d'où il paroit que a est à b comme p à p-½ n. C'est-à-dire que le diametre E A de la Terre, est à son axe P Q, comme 289 à 288½, ou comme 578 à 577; car la raison de p à n estoit comme 289 à 1. Pour trouver en suite quelle est la ligne courbe E D P, je m'imagine le canal plein d'eau E C D, & menant D O perpendiculaire sur l'axe P C, je fais C O ∞ x, & O D | |
[pagina 469]
| |
 [Fig. 131]
∞ y; les autres lignes estant nommées comme devant. Il est certain que l'eau de E C & celle de D C se doivent derechef contrebalancer. Et mesme, cela doit arriver de quelque maniere qu'on conçoive que le canal soit fait, pourvû qu'il aboutisse de part & d'autre à la surface; comme, par ex. s'il alloit par D O C E, ou D O P, ou D C P. Maintenant, la force centrifuge de toute l'eau en C D, est égale à celle de l'eau qui rempliroit le canal O D, supposé de mesme largeur; ce qui se voit facilement par la Mechanique des plans inclinez. Mais comme E C ∞ a, à D O ∞ y, ainsi est la force centrifuge en E, qui estoit n, à la force centrifuge en D; | qui sera donc ny/a. Dont la moitié multipliant le contenu du canal D O ∞ y, fait laGa naar margenoot+ force centrifuge de ce canal ∞ ½nyy/a, qui est donc aussi la force centrifuge du canal C D. Mais la pesanteur de ce canal C D, vers le centre C est 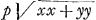 . donc sa pression qui reste vers C, sera . donc sa pression qui reste vers C, sera
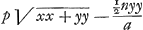 ; qui doit estre égale à pa - ½an, pression du canal E C, trouvée cydevant. ; qui doit estre égale à pa - ½an, pression du canal E C, trouvée cydevant.
Laquelle Equation, en supposant ap/n ∞ f, revient à celle-cy, 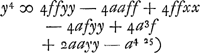 Qui fait voir que la ligne courbe E D P n'est pas une section de Cone, si ce n'est quand p & n sont égales; c'est-a-dire quand la force centrifuge d'un corps, placé en E, est supposée égale à sa pesanteur vers le centre C. Car alors il paroit que f est égale à a; & l'Equation devient 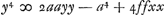 ; ou bient ; ou bient 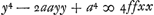 . & enfin . & enfin 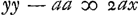 . Ce qui marque qu'en ce cas E D P est une Pa- . Ce qui marque qu'en ce cas E D P est une Pa- | |
[pagina 470]
| |
raboleGa naar voetnoot26), telle que dans cette figure [Fig. 132]; ayant le sommet P; l'axe P C égal à la moitié de C E; & le parametre double de la mesme C E. 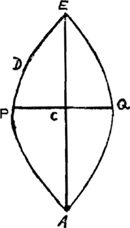 [Fig. 132]
De sorte que si la Terre, ayant le diametre E A de la grandeur qu'il est, tournoit, sur son axe P Q, 17 fois plus viste qu'elle ne fait, (car alors la force centrifuge en E seroit égale à la pesanteur vers le centre, par la demonstration qui est dans |Ga naar margenoot+ ce Discours) elle auroit la figure du corps que font ces deux demies Paraboles opposées, P E C, Q E C, en tournant autour de l'axe P Q. Et on voit que c'est là la plus grande force centrifuge qu'on puisse supposer; par ce que, si on la faisoit plus grande que la pesanteur, les corps placez en E s'envoleroient en l'air. Hors de ce cas, si dans l'Equation trouvée l'on fait yy ∞ a z, estant z une ligne indeterminée, l'on aura 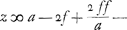 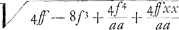 Et mettant d pour ff/a - f, viendra
Et mettant d pour ff/a - f, viendra
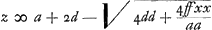 . D'où je connois que, C O estant x, si la perpendiculaire O T est appellée z; le point T sera dans une Hyperbole dont l'axe . D'où je connois que, C O estant x, si la perpendiculaire O T est appellée z; le point T sera dans une Hyperbole dont l'axe
 [Fig. 131]
adjouté à C E sera 4d. Et que comme 4ff à aa, ainsi sera l'axe au parametre; qui sera donc aad/ff, c'est-à-dire a - na/p, en restituant les valeurs de d & de f. Et parce que yy estoit égale à az, il s'ensuit que D O ∞ y sera moyene proportionelle entre O T & E C. D'où l'on peut trouver les points par lesquels la ligne courbe E D P doit passer. Or cette ligne satisfait aussi à ce que j'ay dit estre requis; sçavoir que menant D R qui luy soit à angles | |
[pagina 471]
| |
droits, la raison | de O R à R C sera composée de la raison de p à n, & de E C à C D,Ga naar margenoot+ comme cela se peut prouver par le calcul d'AlgebreGa naar voetnoot28). J'ay supposé dans tout ce raisonnement que la pesanteur est la mesme au dedans de la Terre qu'à sa surface; ce qui me paroit fort vraisemblable, non obstant la raison qu'on peut a voird' en douter, dont je parleray aprés. Mais quand il en seroit autrementGa naar voetnoot29), cela ne changeroit presque rien à ce qui a esté trouvé de la figure de la Terre: mais bien alors quand la force centrifuge fait une partie considerable de la pesanteur, ou qu'elle luy est égale, comme dans le cas de la figure Parabolique, qui alors deviendroit tout autre. Au reste quand la force centrifuge en E est tres petite à raison de la pesanteur, comme elle est icy sur la Terre, l'Hyperbole E T P, à cause du grand éloignement de son centre, approche fort de la Parabole, & par consequent E D P ne differe guere de l'Ellipse; ni guere aussi du cercle, parce que E C alors ne surpasse C P que de fort peu; comme il a esté trouvé peu devant, que cet exces n'est que 1/578 de E C, demidiametre de la Terre. Monsieur Newton le trouve 1/231 de E C, & que ainsi la figure de la Terre differe bien plus de la spherique; se servant en cela d'une tout autre supputation. que je n'examineray pas icy, parce qu'aussi bien je ne suis pas d'accord d'un Principe qu'il suppose dans ce calcul & ailleurs; qui est, que toutes les petites parties, qu'on peut imaginer dans deux ou plusieurs differents corps, s'attirent ou tendent à s'approcher mutuellement. Ce que je ne sçaurois admettre, par ce que je crois voir clairement, que la cause d'une telle attraction n'est point explicable par aucun principe de Mechanique, ni des regles du mouvement. comme je ne suis pas persuadé non plus de la necessité de l'attraction mutuelle des corps entiers; ayant fait voir que, quand il n'y auroit point de Terre, les corps nel aisseroient pas, par ce qu'on appelle leur pesanteur, de tendre vers un centre.| | |
[pagina 472]
| |
Ga naar margenoot+ Je n'ay donc rien contre la Vis Centripeta, comme Mr. Newton l'appelle, par la quelle il fait peser les Planetes vers le Soleil, & la Lune vers la Terre, mais j'en demeure d'accord sans difficulté: parce que non seulement on sçait par experience qu'il y a une telle maniere d'attraction ou d'impulsion dans la nature, mais qu'aussi elle s'explique par les loix du mouvement, comme on a vû dans ce que j'ay écrit cy dessus de la pesanteur. Car rien n'empêche que la cause, de cette Vis Centripeta vers le Soleil, ne soit semblable à celle qui pousse les corps, qu'on appelle pesants, à descendre vers la Terre. Il y avoit long temps que je m'estois imaginé, que la figure spherique du Soleil pouvoit estre produite de mesme que celle qui, selon moy, produit la sphericité de la TerreGa naar voetnoot30); mais je n'avois point etendu l'action de la pesanteur à de si grandes distances, comme du Soleil aux Planetes, ni de la Terre à la Lune; parce que les Tourbillons de Mr. Des Cartes, qui m'avoient autrefois paru fort vraisemblables, & que j'avois encore dans l'esprit, venoient à la traverse. Je n'avois pas pensé non plus à cette diminution reglée de la pesanteur, sçavoir qu'elle estoit en raison reciproque des quarrez des distances du centre: qui est une nouvelle & fort remarquable proprieté de la pesanteur, dont il vaut bien la peine de chercher la raison. Mais voiant maintenant par les demonstrations de Mr. Newton, qu'en supposant une telle pesanteur vers le Soleil, & qui diminue suivant la dite proportion, elle contrebalance si bien les forces centrifuges des Planetes, & produit justement l'effet du mouvement Elliptique, que Kepler avoit deviné, & verifié par les observations, je ne puis guere douter que ces Hypotheses touchant la pesanteur ne soient vrayes, ni que le Systeme de Mr. Newton, autant qu'il est fondé la dessus, ne le soit de mesme. Qui doit paroitre d'autant plus probable, qu'on y trouve la solution de plusieurs difficultez, qui faisoient deGa naar margenoot+ la peine dans les Tourbil|lons supposez de Des Cartes. On voit maintenant comment les excentricitez des Planetes peuvent demeurer constamment les mesmes: pourquoy les plans de leurs Orbes ne s'unissent point, mais gardent leurs differentes inclinaisons à l'égard du plan de l'Ecliptique, & pourquoy les plans de tous ces Orbes passent necessairement par le SoleilGa naar voetnoot31). Comment les mouvemens des Planetes peuvent s'accelerer & se ralentir par les degrez qu'on y observe; qui malaisement pouvoient estre tels, si elles nageoient dans un Tourbillon autour du SoleilGa naar voetnoot32). On y voit enfin | |
[pagina 473]
| |
comment les Cometes peuvent traverser nostre Systeme. Car depuis qu'on sçait qu'elles entrent souvent dans la region des Planetes, on avoit de la peine à concevoir comment elles pouvoient quelquefois aller d'un mouvement contraire à celuy du Tourbillon, qui avoit assez de force pour emporter les PlanetesGa naar voetnoot33). Mais, par la doctrine de Mr. Newton, ce scrupule est encore osté; puisque rien n'y empêche que les Cometes ne parcourent des chemins Elliptiques autour du Soleil, comme les Planetes; mais des chemins plus étendus, & de figure plus differente de la circulaire; & qu'ainsi ces corps n'aient leurs retours periodiques, comme quelques Philosophes & Astronomes anciens & modernes se l'estoient imaginé. Il y a seulement cette difficulté, que Mr. Newton, en rejettant les Tourbillons de Des Cartes, veut que les espaces celestes ne contienent qu'une matiere fort rare, afin que les Planetes & les Cometes rencontrent d'autant moins d'obstacle en leur cours. Laquelle rareté estant posée, il ne semble pas possible d'expliquer ni l'action de la Pesanteur, ni celle de la Lumiere, du moins par les voies dont je me suis servi. Pour examiner donc ce point, je dis que la matiere etherée peut estre censée rare de deux manieres, sçavoir ou que ses particules soient distantes entre elles, avec beaucoup de vuide entre deux; ou qu'elles se touchent, mais que le tissu de chacune foit rare, & |Ga naar margenoot+ entre-meslé de beaucoup de petits espaces vuides. Pour ce qui est du vuide, je l'admets sans difficulté, & mesme je le crois necessaire pour le mouvement des petits corpuscules entre eux. n'estant point du sentiment de Mr. Des Cartes, qui veut que la seule étendue fasse l'essence du corps; mais y adjoutant encore la dureté parfaite, qui le rende inpenetrable, & incapable d'estre rompu ni écorné. Cependant à considerer la rareté de la premiere, je ne vois pas comment alors on pourroit rendre raison de la Pesanteur: & quant à la Lumiere, il me semble entierement impossible, avec de tels vuides, d'expliquer sa prodigieuse vitesse, qui doit estre six cent mille fois plus grande que celle du Son, suivant la demonstration de Mr. Romer, que j'ay raportée au Traité de la Lumiere. C'est pourquoy je tiens qu'une telle rareté ne sçauroit convenir aux espaces celestes. Il y a plus d'apparence de la concevoir de l'autre façon; parce que les particules s'y peuvent toucher, comme je les ay supposées au dit Traité, & toutefois, à cause de la legereté de leur tissu, resister fort peu au mouvement des Planetes. Car que sçait on jusqu'où la nature peut aller à composer des corps durs, avec peu de matiere; sur tout, si des particules tres menues & deliées, ou mesme creusesGa naar voetnoot34), peuvent estre infiniment | |
[pagina 474]
| |
fortes. Mais je crois que, sans considerer la rareté, la grande agitation de la matiere etherée, peut contribuer beaucoup à sa penetrabilité. Car si le petit mouvement des particules de l'eau la rend liquide, & de beaucoup moindre resistence, à l'égard des corps qui nagent dedans, que n'est le sable ou quelque poudre tres fine; ne faut il pas qu'une matiere plus subtile, & insiniment plus agitée, soit aussi d'autant plus aisée à penetrer? Quoy qu'il en soit, nous voions que la nature ne manque pas d'industrie, pour faire qu'il y ait des espaces, dans lesquels les corps se meuvent avec tres peu de resistence; carGa naar margenoot+ cela pa | roit par ce que nos mains sentent dans l'air, & encore plus par les experiences qu'on fait dans les vaisseaux de verre, dont on a tiré tout l'air; où la plume la plus legere, descend avec la mesme vitesse qu'une balle de plomb. Que si on vouloit soutenir que cela procede de la grande rareté de la matiere qui reste dans ce vuide d'air; j'alleguerois au contraire qu'on y aperçoit l'effet d'une matiere qui pese fort considerablementGa naar voetnoot35), comme on a vû dans l'experience cy dessus raportée. Quant au raisonnement de Mr. Newton dans la Prop. 6. du Livre 3. pour prouver l'extreme rareté de l'ether: sçavoir que les pesanteurs des corps sont comme les quantitez de la matiere qu'ils contienent; & que, cela estant, si les espaces de l'air ou de l'éther estoient aussi pleins de matiere que l'or & l'argent, ces metaux n'y descendroient pas; parce qu'un corps solide, n'ayant pas une plus grande pesanteur specifique qu'un fluide, n'y sçauroit enfoncer. je dis que je suis d'accord que les pesanteurs des corps suivent les quantitez de leur matiere; & je l'ay mesme demontré dans ce present Discours. Mais j'ay aussi fait voir, qu'à ces corps que nous appellons pesants, la pesanteur peut bien estre imprimée par la force centrisuge d'une matiere, qui ne pese point elle mesme vers le centre de la Terre, à cause de son mouvement circulaire & tres rapide; mais qui tend à s'en éloigner. Cette matiere donc peut fort bien remplir tout l'espace autour de la Terre, que d'autres corpuscules n'occupent point, sans que cela empesche la descente des corps qu'on appelle pesants; estant au contraire la seule cause qui les y oblige. Ce seroit autre chose si on supposoit que la pesanteur fust une qualité inherente de la matiere corporelle. Mais c'est à quoy je ne crois pas que Mr. Newton consente, parce qu'une telle hypothese nous eloigneroit fort des principes Mathematiques ou Mechaniques. Ga naar margenoot+ Il me dira peutestre, que, quand on m'auroit accordé | que la matiere etherée consiste en des particules qui se touchent, pour transmettre la lumiere; on ne verroit pas | |
[pagina 475]
| |
pourtant qu'elle observeroit cette regle de ne s'étendre qu'en ligne droite, comme elle fait; parce que cela est contre sa Propos. 42. du 2 Livre. qui dit que le mouvement, qui se repand dans une matiere fluide, ne s'etend pas seulement tout droit depuis son origine, apres avoir passé par quelque ouverture, mais qu'il s'ecarte aussi à costé. A quoy je repons par avance, que ce que j'ay allegué, pour prouver que la lumiere (horsmis en la reflexion ou en la refraction) ne s'etend que directement, ne laisse pas de subsister non obstant la dite Proposition. Parce que je ne nie pas que, quand le Soleil luit à travers une fenestre, il ne se repande du mouvement à costé de l'espace eclairé; mais je dis que ces ondes detournées sont trop foibles pour produire de la lumiere. Et quoy qu'il veuille que l'emanation du Son prouve que ces epanchemens à costé sont sensibles, je tiens pour assuré qu'elle prouve plustost le contraire. Par ce que si le Son, ayant passé par une ouverture, s'etendoit aussi à costé, comme veut Mr. Newton, il ne garderoit pas si exactement, dans l'Echo, l'égalité des angles d'incidence & de reflexion; en sorte que quand on est placé en un lieu, d'où il ne peut point tomber de perpendiculaire sur le plan reflechissant d'un mur un peu eloigné, on n'entend point repondre l'Echo au bruit qu'on fait en ce lieu, comme je l'ay experimenté tres souvent. Je ne doute pas aussi, que l'experience qu'il apporte du Son, qu'on entendroit non obstant une maison interposée, ne se trouvast tout autre, pourvû que cette maison fust placée au milieu de quelque grande eau, ou en sorte qu'il n'y eust rien autour, qui pust renvoier quelque parcelle du Son par reflexion. Et pour ce qu'il dit, qu'en quelque endroit qu'on soit dans une chambre, dont la fenestre est ouverte, on y entend le Son de dehors, non pas par la reflexion des murailles, mais venant | directement de la fenêtre; on voit combien il est facile de s'y abuser, àGa naar margenoot+ cause de la multitude des reflexions reïterées, qui se font comme dans un instant; de sorte que le Son, qui s'entend comme venant immediatement de la senétre ouverte, en peut venir, ou des endroits fort proches, aprés une double reflexion. J'avouë donc, que pour ce qui est des ondulations ou cercles qui se font à la surface de l'eau, la chose se passe à peu pres comme l'assure Mr. Newton: c'est à dire qu'une onde, aprés avoir passé l'ouverture, se dilate en suite d'un costé & d'autre, & toutefois plus foiblement là que dans le milieu. Mais pour le Son, je dis que ces emanations par les costez, sont presque insensibles à l'oreille: & qu'en ce qui est de la lumiere, elles ne font point d'effet du tout sur les yeuxGa naar voetnoot36). J'ay crû devoir aller au devant de ces objections que pouvoit suggerer le Livre de Mr. Newton, sçachant la grande estime qu'on fait de cet ouvrage, & avec raison; puis qu'on ne sçauroit rien voir de plus sçavant en ces matieres, ni qui temoigne une | |
[pagina 476]
| |
plus grande penetration d'esprit. Il me reste encore deux choses à remarquer dans son Systeme, qui me semblent fort belles, & qui me donneront occasion de faire quelque reflexion. Aprés quoy j'adjouteray ce que j'ay trouvé parmi mes papiers touchant le mouvement des corps à travers l'air, ou autre milieu qui resiste; duquel mouvement il traite au long dans le livre 2. On a vû comment dans le Systeme de Mr. Newton les pesanteurs, tant des Planetes vers le Soleil, que des Satellites vers leurs Planetes, sont supposées en raison double reciproque de leurs distances du centre de leurs Orbes. Ce qui se confirme admirablement par ce qu'il demontre touchant la Lune; sçavoir que sa force centrifuge, que luy donne son mouvement, égale precisement sa pesanteur vers la Terre, & qu'ainsi cesGa naar margenoot+ deux sorces contraires la tienent suspendue là où elle est. Car la | distance d'icy à la Lune estant de 60 demidiametres de la Terre, & partant la pesanteur, dans sa region, 1/3600 de celle que nous sentons; il faloit que la force centrifuge d'un corps, qui se mouvroit comme la Lune, égalast de mesme 1/3600 du poids qu'il auroit à la surface de la Terre. Ce qui se trouve effectivement ainsi, & le calcul s'en peut faire aisément, puis qu'on sçait desja que la force centrifuge sous l'Equateur est 1/289 de nostre pesanteur icy bas. Mais puisque cet exemple de la Lune prouve si bien la diminution du poids, suivant la raison reciproque des quarrez des distances du centre de la Terre; on pourroit douter s'il n'y auroit pas aux Pendules une autre inégalité, outre celle qui estoit causée par le mouvement journalier. Car si la Terre n'est pas spherique, mais assez pres spheroïde, & qu'un point sous l'Equateur est plus eloigné du centre, que n'est un point sous le Pole, dans la raison de 578 à 577, comme il a esté dit cy-devant; les pesanteurs estant en ces endroits en raison contraire des quarrez des distances, il faudroit aussi que le pendule sous l'Equateur fust plus court, que celuy dessous le Pole, dans cette mesme raison contraire. C'est à dire que ces pendules seroient comme 288 à 289; ou que le pendule sous l'Equateur seroit plus court de 1/289 de ce qu'il feroit sous le Pole. Qui est justement la mesme difference, qui provenoit cy dessus du mouvement journalier, ou de la force centrifuge. De sorte qu'une Horloge, avec la mesme longueur de pendule, iroit plus lentement sous l'Equateur que sous le Pole, du double de ce qu'elle retardoit par le mouvement de la Terre; & ainsi cette difference journaliere sous l'Equateur seroit de pres de 5 minutes. Et sous les autres paralleles, on la trouveroit par tout plus que double de ce qu'elle y estoit auparavant. Mais je doute fort que l'experience confirme cette grande variationGa naar voetnoot37), puisque j'ay vû que, dans le voiageGa naar voetnoot36) | |
[pagina 477]
| |
dont j'ay fait mention, la seule premiere équation suffit, & que la plus que double mettroit, vers | le milieu du chemin, trop de difference entre la route du vaisseau,Ga naar margenoot+ calculée sur le Pendule, & celle qu'il tenoit par l'Estime des Pilotes. Et pour rendre raison pourquoy la seconde variation n'auroit point lieu, je dis qu'il ne seroit pas étrange si la pesanteur, prés de la surface de la Terre, ne suivoit pas precisement, ainsi que dans les regions plus élevées, la diminution que font les differentes distances du centreGa naar voetnoot38); parce qu'il se peut que le mouvement de la matiere qui cause la pesanteur, soit aucunement alteré dans la proximité de la Terre. comme il l'est apparemment au dedans: puisque sans cela il faudroit dire que la pesanteur, en allant vers le centre, augmenteroit â l'infini; ce qui n'est point vraisemblable. Au contraire, selon Mr. Newton, la pesanteur au dedans de la Terre diminue suivant que les corps approchent du centre; mais il se sert à le prouver de son principe, dont j'ay dit que je ne suis pas d'accord. Ce qui me reste à remarquer touchant son Systeme, & qui m'a fort plû, c'est qu'il trouve moyen, en supposant la distance d'icy au Soleil connue, de definir quelle est la pesanteur que sentiroient les habitans de Saturne & de Jupiter, comparée à la nostre icy sur la Terre, & quelle encore est sa mesure à la surface du SoleilGa naar voetnoot39). Choses qui d'abord semblent bien éloignées de nostre connoissance; & qui pourtant sont de consequences des principes que j'ay raportez peu devant. Cette determination a lieu dans les Planetes qui ont un ou plusieurs Satellites, parce que les temps periodiques de ceux cy, & leur distances des Planetes qu'ils accompagnent, doivent entrer dans le calcul. Par lequel Mr. Newton trouve les pesanteurs aux surfaces du Soleil, de Jupiter, de Saturne, & de la Terre, dans la raison de ces nombres, 10000, 804½, 536, 805½. Il est vray qu'il y a quelque incertitude à cause de la distance du Soleil, qui n'est pas assez bien connuë, & qui a esté prise dans ce calcul d'environ 5000 diametres de la Terre, au | lieu que, suivant la dimension de Mr. Cassini, elle estGa naar margenoot+ environ de 10000, qui approche assez de ce que j'avois autrefois trouvé, par des raisons vraisemblables, dans mon Systeme de Saturne, sçavoir 12000Ga naar voetnoot40). Je differe aussi quelque chose en ce qui est des diametres des Planetes. De sorte que, par ma supputation, la pesanteur dans Jupiter, à celle que nous avons icy sur la Terre, se trouve comme 13 à 10, au lieu que Mr. Newton les fait égales, ou insensiblement differentes. Mais la pesanteur dans le Soleil, qui, par les nombres qu'on vient de voir, estoit environ 12 fois plus grande que la nostre sur la Terre, je la trouve 26 fois plus grande D'où s'ensuitGa naar voetnoot41), en expliquant la pesanteur de la façon quej'ay fait, que la matiere fluide, | |
[pagina 478]
| |
aupres du soleil, doit avoir une vitesse 49 fois plus grande que celle que nous avons trouvée pres de la Terre; qui estoit desià 17 fois plus grande que la vitesse d'un point sous l'Equateur. Voila donc une terrible rapidité; qui m'a fait penser si elle ne pouroit pas bien estre la cause de la lumiere eclatante du Soleil, supposé que la lumiere soit produite comme je l'explique dans ce que j'en ay écrit; sçavoir de ce que les particules Solaires, nageant dans une matiere plus subtile & extremement agitée, frappent contre les particules de l'Ether qui les environnent. Car si l'agitation d'une telle matiere, avec le mouvement qu'elle a icy sur la Terre, peut causer la clarté de la flamme d'une chandelle, ou du Camphre allumé, combien plus grande fera t'elle cette clarté par un mouvement 49 fois plus prompt & plus violent? J'ay vu avec plaisir ce que Mr. Newton écrit touchant les chûtes & les jets des corps pesants dans l'air, ou dans quelqu'autre milieu qui resiste au mouvement; m'estant appliqué autrefoisGa naar voetnoot42) à la mesme recherche. Et puisque cette matiere appartient en partie à celle de la Pesanteur, je crois pouvoir raporter icy ce que j'en decouvris alors.Ga naar margenoot+ Ce que je ne feray pourtant qu'en | abregé & sans y joindre les demonstrations; ayant negligé de les achever, parce que cette speculation ne m'a pas semblé assez utile, ni de consequence, à proportion de la difficulté qui s'y rencontre. J'examinay premierement ces mouvemens, en supposant que les forces de la Resistance sont comme les Vitesses des corps, ce qui alors me paroissoit fort vraisemblable. Mais ayant obtenu ce que je cherchois, j'appris presque en mesme temps, par les experiences que nous fîmes à Paris dans l'Academie des Sciences, que la resistence de l'air, & de l'eau, estoit comme les quarrez des vitessesGa naar voetnoot43). Et la raison est assez aisée à concevoir; parce qu'un corps, allant par exemple avec double vitesse, est rencontré par deux fois autant de particules de l'air ou de l'eau, & avec double celerité. Ainsi je vis ma nouvelle Theorie renversée, ou du moins inutile. Apres quoy je voulus aussi chercher ce qui arrive lors qu'on suppose ce veritable fondement des Resistances; où je vis que la chose estoit beaucoup plus difficile, & sur tout en ce qui regarde la ligne courbe que parcourent les corps jettez obliquement. Dans la premiere supposition, où les resistances sont comme les vitesses, je remarquay que, pour trouver les espaces passez en de certains temps, lors que les corps tombent ou montent perpendiculairement, & pour connoitre les vitesses au bout de ces temps, il y avoit une ligne courbe, que j'avois examinée long temps auparavant, qui estoit de grand usage en cette recherche. On la peut appeller la Logarithmique ou la Logistique, car je ne vois pas qu'on luy ait encore donné de nom, quoyque | |
[pagina 479]
| |
d'autres l'aient encore considerée cy devantGa naar voetnoot44). Cette ligne infinie estant A B C, [Fig. 133] elle a une ligne droite pour Asymptote, comme D E; dans la quelle si on prend des parties égales quelquonques qui se suivent, comme D G, G F, & que l'on tire des points D, G, F, des perpendiculaires jusqu'à la courbe, sça | voir, D A.Ga naar margenoot+
 [Fig. 133]
G H, F B, ces lignes seront proportionelles continues. D'oû l'on voit qu'il est aisé de trouver autant de points qu'on veut dans cette courbe; de la quelle je raporteray par apres quelques proprietez qui meritent d'estre considerées. Pour expliquer ce qui est des chûtes des corps, je repete icy premierement ce que j'ay écrit à la fin du Traité du Centre d' AgitationGa naar voetnoot45): sçavoir qu'un corps, en tombant à travers l'air, augmente continuellement sa vitesse, mais toutefois en sorte qu'il n'en peut jamais exceder, ni mesme atteindre, un certain degré; qui est la vitesse qu'il faudroit à l'air à soufler de bas en haut, pour tenir le corps suspendu sans pouvoir descendre; car alors, la force de l'air contre ce corps, égale sa pesanteur. J'appelle cette vitesse, dans chaque corps, la vitesse Terminale. | |
[pagina 480]
| |
Si donc un corps pesant est jetté perpendiculairement en haut, avec une vitesse dont la raison à la vitesse Terminale soit donnée, par exemple comme de la partie A K à K D dans l'ordonnée A D, perpendiculaire à l'asymptote D E; soit menée K B parallele à cette asymptote, & qu'au point B la courbe soit touchée par la droite B O, qui rencontre D E en O, & D A en Q. Laquelle tangente se trouve en prenant F O, depuisGa naar margenoot+ l'ordonnée | B F; égale à une certaine longueur, qui pour toutes les tangentes est la mesme, & que je definiray dans la suite. Puis soit A C parallele à cette tangente, coupant K B prolongée en P; & du point C, où elle rencontre la courbe, soit tirée C L M, parallele à A D, & coupant K B prolongée, & A M parallele à l'asymptote, aux points L & M. Maintenant le temps que le corps met à monter à la hauteur où il peut arriver, est au temps de sa descente de cette mesme hauteur, comme la ligne K B à B LGa naar voetnoot46). Et le temps qu'il emploie à monter à travers l'air, estant jetté comme il a esté dit, est au temps qu'il emploieroit sans rencontrer de resistence, comme K B à K PGa naar voetnoot47). Et la hauteur à laquelle il montera dans l'air, à celle où monteroit sans resistence, comme l'espace A B K au triangle A P KGa naar voetnoot48), ou comme Q A à A X, queje suppose estre la moitié d'une troisieme proportionelle aux lignes D K, K AGa naar voetnoot49). Et sa vitesse, en commençant de monter, à celle qu'il a en retombant à terre, comme M L à L CGa naar voetnoot50). On trouve de plus, par cette mesme ligne, quelle est la courbe que parcourt un corps jetté obliquement. Car, dans la mesme figure, [Fig. 134] si l'angle du jet, sur la ligne horizontale, est L M R, avec une vitesse donnée, dont le mouvement en | |
[pagina 481]
| |
haut soit à la vitesse Terminale comme A K à K D: soit repetée la construction precedente, & que la droite A S, qui touche la courbe A B C en A, rencontre K B en S. Puis comme S P à P B ainsi soit R L à L T, & sur la base M C soit dressée une figure proportionelle au segment A B C P, en sorte que les paralleles & également distantes de l'asymptote D E, dans l'une & l'autre figure, aient par tout la mesme raison de B P à T L. Ce sera la courbe M T C qui marquera la figure requise du jetGa naar voetnoot51). Et parce que la hauteur de l'élevation avec resistance, estoit à la hauteur du jet libre, comme Q A à A X; si l'on fait que T L ait cette mesme raison à une autre ligne V Z; ce sera la hauteur | de la Parabole M V que fait ce jet libre, commencé en MGa naar margenoot+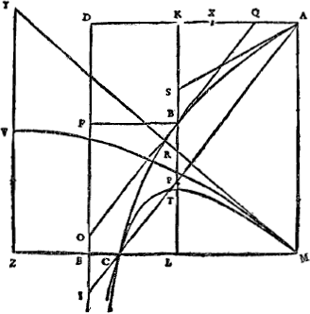 [Fig. 134]
avec la mesme force, & dans la mesme direction M R, qu'avoit l'autre jet. De sorte que si dans l'angle L M R on ajuste Y Z perpendiculaire à M C, & égale à la double V Z, on aura le sommet de cette parabole en V au milieu de Y Z, & sa demie base ou demie amplitude M Z. Il est à noter que, quel que soit l'angle d'elevation L M R, pourvu que la vitesse verticale demeure la mesme, on trouve icy la mesme amplitude M C. Mais il faut estre averti que ce sont seulement les figures des jets qu'on trouve de cette façon, & | |
[pagina 482]
| |
non pas les hauteurs & amplitudes de divers jets comparez ensemble. Car ils doiventGa naar margenoot+ tous estre de mesme hauteur, quand la cele | rité verticale est la mesme. C'est pourquoy alors chaque figure de jet, ainsi trouvée, doit estre reduite à une figure proportionelle d'égale hauteur, si on veut sçavoir comment les amplitudes, & les hauteurs des divers jets, sont les unes aux autres. J'adjoute encore icy, que la ligne Logarithmique ne sert pas seulement à trouver les courbes des jets, mais qu'elle est cette courbe elle mesme en un cas, sçavoir quand on jette un corps obliquement en bas, en sorte que ce qu'il y a de descente perpendiculaire, égale la vitesse TerminaleGa naar voetnoot52). Car alors ce corps suivra precisement la courbure d'une telle ligne, en s'approchant tousjours de l'asymptote, sans la pouvoir atteindre. Et ce qui determine l'espece de la ligne, c'est que sa Soutangente, (je nommeray ainsi la ligne F O, qui pour toutes les tangentes est la mesme) sera double de la hauteur à laquelle la vitesse Terminale pent faire monter le corps, sans resistance du milieuGa naar voetnoot53). Ce sont là les choses que je trouvay en supposant la resistance estre comme la vitesse, mais toute cette Theorie estant, comme j'ay dit, fondée sur un principe, que la nature ne suit point en ce qui est des resistances de l'air & de l'eau, je la negligeay entierement; & ce n'est qu'à l'occasion du Traité de Mr. Newton que je l'ay reprise, pour voir si ce que nous avions cherché par des voies fort differentes, s'accordoit ensemble comme il faloit. Ce qui se trouve ainsi: car la construction pour la ligne du jet, qu'il donne dans la Propos. 4 du 2 Livre, quoyque tout autre que la miene & plus difficile, produit pourtant la mesme courbe, comme cela se peut prouver par demonstrationGa naar voetnoot54). En examinant ce qui arrive dans la vrayeGa naar voetnoot55) hypothese de la Resistance, qui est en raison double de la Vitesse, j'avois seulement determiné ce cas particulier, d'un corps | |
[pagina 483]
| |
jetté en haut avec sa vitesse Terminale; sçavoir que le temps de toute son élevation en l'air, est au temps qu'il emploieroit à monter jusqu'où | il peut sans resistance,Ga naar margenoot+ comme le Cercle au Quarré qui luy est circonscrit. Et que la hauteur du premier jet est à la hauteur de l'autre, comme l'espace entre une Hyperbole & son asymptote, terminé par deux paralleles à l'autre asymptote qui soient en raison de 2 à 1, au rectangle où parallelogramme de la mesme Hyperbole. C'est-à-dire, comme, dans la figure suivante, l'espace A M D K au quarré A CGa naar voetnoot56). Je n'avois point recherché les autres cas, qui sont compris universellement dans la Prop. 9, du 2. Livre de Mr. Newton, qui est tresbelle: & ce qui m'en empêcha, ce fut que je ne trouvois point, par la voie que je suivois, la mesure des descentes des corps, si non en supposant la quadrature de certaine Ligne courbe, que je ne sàavois pas qu'elle dependoit de la quadrature de l'Hyperbole. Je reduisis la dimension de l'espace de cette courbe, à une Progression infinie, a + ⅓a3 + ⅕a5 + 1/7a7 &c. Ne sçachant pas que la mesme progression donnoit aussi la mesure du secteur Hyperbolique: ce que j'ay vu depuis, en comparant la demonstration de Mr. Newton avec ce que j'avois trouvéGa naar voetnoot57). Mais par ce que cette Progression, pour la mesure de l'Hyperbole, n'a pas encore esté remarquée que je sçache, je veux expliquer icy comment elle y sert. Soit A B [Fig. 135] une Hyperbole, dont les asymptotes D C, C E, fassent un angle droit. le demi axe soit C A, perpendiculaire à D A E qui touche l'Hyperbole; & que A C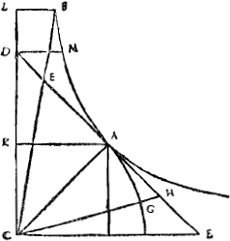 [Fig. 135]
B soit un Secteur, la ligne C B coupant A D en F. Si on prend maintenant A C ou A D pour l'unité, & que A F soit nommée a, qui est une fraction moindre que l'unité, quand A F, A D sont commensurables; je dis que, comme la somme de la Progression infinie a + ⅓a3 + ⅕a5 + 1/7a7, &c. à 1, ainsi sera le Secteur A C B au triangle A C D. Ou si on mene les perpendiculaires A K, B L sur l'asymptote, on peut dire la mesme chose de l'espace A B L K, qui est egal à ce Secteur, comme on voit aisement par l'égalité des triangles C A K, C B L. De sorte que cette Pro | gression pour l'Hyperbole,Ga naar margenoot+ respond à celle qu'a donné Mr. Leibnits pour le CercleGa naar voetnoot58). par la quelle, si le Secteur du Cercle est A C G, ayant pour rayon A C, & que C G coupe A E en H; A H estant nom- | |
[pagina 484]
| |
mée a, & A E égale à 1; la somme de la Progression a - ⅓a3 + ⅕a5 - 1/7a7 &c. est à 1, comme le Secteur A C G au triangle A C E, ou comme l'arc A G à la droite A E. Pour ce qui est de la ligne du jet oblique; s'il suffisoit, dans cette maniere de resistance, de connoitre le mouvement horizontal & le vertical d'un corps, pour en composer le mouvement oblique, ainsi que dans la premiere hypothese, il y auroit moyen de determiner des points par où cette ligne doit passer: & la mesme ligne Logarithmique y seroit utile, estant tournée en sorte que son asymptote fust parallele à l'horizon; & elle mesme seroit derechef la courbe du jet, dans le cas ou j'ay dit qu'elle servoit auparavant. Mais cette composition de mouvement n'ayant point lieu icy; parce que la diminution du mouvement retardé, dans la diagonale d'un rectangle, n'est pas proportionelle aux diminutions par les costez; il est extremement difficile, si non du tout impossiblee, de resoudre ce ProblemeGa naar voetnoot59). Le mouvement horizontal estant consideré à part, comme d'une boule qui rouleroit sur un plancher uni, a cela de remarquable icy, qu'il doit aller loin à l'infini, non-obstantGa naar margenoot+ la resistance | du milieu, au lieu que, quand la resistance est comme la vitesse, il est borné, & n'atteint jamais un certain terme. Et cette infinité se prouve aisement par la Propos. 5. du 2 Livre du Traité de Mr. Newton, parce que l'espace compris entre l'Hyperbole & ses asymptotes est de grandeur infinieGa naar voetnoot60). Les proprietez de la ligne Logistique, que j'ay promis de raporter, & dont quelques unes ont servi à trouver ce que j'ay remarqué touchant les mouvemens à travers l'air, 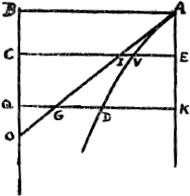 [Fig. 136]
sont les suivantes; outre la premiere, que j'ay desia indiquée, de la proportionalité des ordonnées à l'asymptote, quand elles sont également distantes, par laquelle on trouve des points dans cette ligne. 1. Que les espaces compris entre deux ordonnées à l'asymptote, sont entre eux comme les differences de ces ordonnéesGa naar voetnoot61). Ainsi dans cette figure [Fig. 136], où A V D est la Logistique, B O son asymptote, & les ordonnées A B, V C, D Q; dont ces dernieres, estant continuées, rencontrent A K, parallele à l'asymptote, en E, K; les espaces A B C V, A B Q D sont entre eux comme les droites E V, K D. 2. Que les mesmes choses estant posées, & A O | |
[pagina 485]
| |
estant la tangente au point A, laquelle coupe C E, Q K, en I & G; les espaces A V E, A D K sont entre eux comme les droites V I, D GGa naar voetnoot62). 3. Que l'espace compris entre deux ordonnées, est à l'espace infini, qui, depuis la moindre de ces ordonnées, s'étend entre la Logistique & son asymptote, comme la difference | des mesmes ordonnées est à la moindre. Quand je dis que l'espace infini aGa naar margenoot+ une certaine raison à un espace fini, cela signifie qu'il aproche si prés de la grandeur d'un espace donné, qui a cette proportion à l'espace fini, que la difference peut devenir moindre qu'aucun espace donné. Dans la figure precedente l'espace A B Q D est à l'espace infini, qui depuis D Q s'étend entre la courbe & l'asymptote, comme K D à D QGa naar voetnoot63). 4. Que la Soutangente, comme B O dans la mesme figure, est tousjours d'une mesme longueur, à quelque point de la Logistique que la tangente apartieneGa naar voetnoot64). 5. Que cette longueur se trouve par approximation, & qu'elle est à la partie de l'asymptote, comprise entre les ordonnées de la raison double, comme 434294481903251804 à 301029995663981195; ou, bien pres, [Fig. 133]
comme 13 à 9Ga naar voetnoot65). 6. Que s'il y a trois ordonnées, comme dans cette figure sont A D, H G, B F, & que du point de la courbe, apartenant à la moindre, on mene une parallele à l'asymptote qui coupe les deux autres ordonnées en R & K, & une tangente B Q qui les coupe en N & Q; les espaces trilignes A B K, H B R sont entre eux, comme les parties des ordonnées entre la courbe & la tangente, sçavoir comme A Q, H NGa naar voetnoot66). 7. Que l'espace infini entre une ordonnée,Ga naar margenoot+ la Logistique, & son asymptote, du costé que ces deux dernieres vont en s'approchant, est double du triangle que font l'ordonnée, la tangente menée du mesme point que l'ordonnée, & la soutangente. Ainsi, dans la mesme figure, l'espace infini, depuis l'ordonnée B F, est double du triangle B F OGa naar voetnoot67). | |
[pagina 486]
| |
8. Que l'espace, compris entre deux ordonnées, est égal au rectangle de la soutangente & de la difference des mesmes ordonnées. Ainsi, dans la mesme figure, l'espace A D F B est égal au rectangle de la soutangente F O & de K AGa naar voetnoot68). 9. Que le solide que fait l'espace infini depuis une ordonnée, en tournant autour de l'asymptote, est sesquialtere du Cone, dont la hauteur est egale à la soutangente, & le demidiametre de la base égal à la mesme ordonnée. Ainsi le solide que fait l'espace insini B F O C, en tournant autour de F O, est sesquialtere du cone que fait le triangle B F O, en tournant autour de la mesme F OGa naar voetnoot69). 10. Que le solide produit par le mesme espace infini, en tournant autour de l'ordonnée B F, depuis laquelle il commence, est sextuple du cone que fait le triangle B F O, par sa conversion sur B FGa naar voetnoot70). De laquelle mesure des solides il s'ensuit; 11. Que le centre de gravité de l'espace infini, depuis une ordonnée, est distant de cette ordonnée, de la longueur de la soutangenteGa naar voetnoot71).  [Fig. 133]
12. Que ce mesme centre de gravité est de l'asymptote, du quart de l'ordonnéeGa naar voetnoot71). 13. J'avois aussi trouvé que le centre de gravité du premier des dits solides infinis, est distant de sa base, de la moitié de la soutangenteGa naar voetnoot72). 14. Et que le centre de gravité de l'autre solide est distant de sa base infinie, d'une huitieme de son axeGa naar voetnoot73). 15. On sçait assez que cette ligne LogistiqueGa naar margenoot+ sert à la Qua | drature de l'Hyperbole, depuis les demonstrations du P. Greg. de St. Vincent, touchant les espaces Hyperboliques compris entre deux ordonnées sur une des asymptotesGa naar voetnoot74). Et que s'il y a deux tels espaces, dont les ordonnées de l'un soient comme A D à H G dans la derniere figure, & les ordonnées de l'autre comme B F à C E; ces | |
[pagina 487]
| |
espaces seront entre eux comme les lignes D G à F E. Mais on n'a point remarqué, que je sçache, que ces mesmes espaces Hyperboliques sont au Parallelogramme de l'Hyperbole (j'appelle ainsi le parallelogramme dont les costez sont les deux ordonnées sur les asymptotes, tirées d'un mesme point de la Section) comme chacune des lignes D G, F E, à la soutangente F O. De sorte que, si le Parallelogramme de l'Hyperbole est supposé de 0,4342944819 parties, chaque espace Hyperbolique, compris entre deux ordonnées à une des asymptotes, sera à ce parallelogramme, comme le Logarithme de la proportion des mesmes ordonnées, c'est à dire comme la difference des Logarithmes, des nombres qui expriment la proportion des ordonnées, au nombre 0,4342944819; en prenant des Logarithmes de 10 characteres outre la characteristiqueGa naar voetnoot75). | |
[pagina 488]
| |
Ga naar margenoot+ Et d'icy il est aisé de verifier la Quadrature de l'Hyperbole que j'ay donnée dans le Traité de l'Evolution des Lignes Courbes, qui est dans mon Horologium OscillatoriumGa naar voetnoot76). |
|