Oeuvres complètes. Tome XXI. Cosmologie

[p. 25]

I.

Projet de déterminer la méridienne et la latitude de Paris, manière de trouver les ascensions droites et les déclinaisons des étoiles fixes et en même temps l'obliquité de l'écliptique et la quantité de la réfraction atmosphérique pour les étoiles, détermination de cette même quantité pour le soleil, observation d'une éclipse du soleil, discours sur la construction de tables exactes du mouvement des astres.
[1666 et 1667]

Cette Pièce est tirée des ‘Registres de Mathematiques’ dits ‘de l'Année 1667 et d'une partie de l'année 1668 iusqu'au mois d'Auril’. C'est le T. II des Registres, ou plutôt le T. I devenu T. II d'après la correction de feu l'archiviste de l'Académie P. Dorveaux; voyez les p. 180 et 680 du T. XIX; cette correction nous semble arbitraire vu que le tome contient aussi, malgré son titre, des pièces de 1666¹⁾.

§ 1. P. 1 (feuille collée dans le Registre). Mr. Auzout. ‘Les deux premieres observations astronomiques sont la ligne Meridienne, et la hauteur du Pole²⁾, et quoyqu'il y ait diverses manieres de prendre l'une et l'autre, il faut mettre au premier rang celles qui ne supposent point d'observations precedentes, ou l'on puisse auoir erré.

Si ces observations se pouuoient faire en toute sorte de temps on n'auroit rien a souhaitter, mais la hauteur du Pole suppose un certain temps de l'année qui dure environ un mois, depuis la fin de Decembre iusqua la fin de Januier, quand l'Etoile Polaire en une mesme nuit peut estre obseruée dans sa plus grande, et dans sa plus petite hauteur.

1) A la p. 20 du tome - voyez le § 9 qui suit - se trouve la date du 2 juillet 1666: il y est question de l'observation - voyez le titre de la présente Pièce - de l'éclipse du soleil de ce jour dont nous avons déjà fait mention dans l'Avertissement. Toutefois nous avons dû dire dans l'Avertissement que la date précise de la présente Pièce est indéterminable, qu'elle peut fort bien être postérieure à la Pièce de Huygens qui constitue le § 11 qui suit. Voyez encore sur Huygens et Auzout la note 5 qui suit.

2) On a vu dans le T. XIX (p. 255) que le programme de 1666 de Huygens débute, conformément à la note, ou le discours, d'Auzout, par l'alinéa: 1. Trouver la ligne meridiene et la hauteur du pole de Paris, qui sont les fondements de toutes autres observations astronomiques.

[p. 26]

Pour la ligne meridienne, on la peut prendre en tout temps par le moyen des estoilles, pourveu que l'on ait des Instruments bien iustes³⁾, c'est pourquoy il semble plus a propos de commencer par cette obseruation, puisqu'elle suppose le moins, et qu'il est mesme a propos de l'auoir pour la hauteur du Pole.

La maniere de la tracer est par le moyen d'une Etoille telle qu'on voudra, pourvue qu'elle soit hors des refractions⁴⁾, ou prend de cette Etoile deux hauteurs égales deuant et apres qu'elle est arriueé au meridien du lieu, marquant en mesme temps les Azimuths de l'Etoile, car ayant diuisé ces deux Azimuths par la moitié, nous aurés la ligne meridienne.

Il faut pour cela aussi un azimuthal ioint au quart de Cercle pour prendre en mesme temps la hauteur et l'Azimuth, ou auoir un azimuthal a part auec des filets⁵⁾ ou autrement, et qu'il y ait deux Obseruateurs qui prennent en mesme temps l'un la hauteur, et l'autre l'azimuth: ce qu'il y a de commode est que si on a pris une hauteur du costé d'Orient en un jour, on peut quelques iours apres prendre l'autre hauteur egale vers l'Occident.

Ce que l'on fait par le moyen des Etoilles en tout temps, se fait par le moyen du Soleil en un certain temps quelques iours deuant et apres le Solstice d'Esté, quand l'on scait que le soleil ne change point sensiblement de declinaison, et il y a cela de commode que l'on peut tracer son azimuth ... par son ombre, si l'on n'a pas d'instrument, ou se servir de l'Equaire meridienne sans l'embarras de grands Instruments, comme il est necessaire aux Etoilles’ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 2. P. 3 et 4. M. Hugens. [Détermination de la méridienne]. Par le moyen d'un sil perpendiculaire sur un plan horizontal l'on pourra obseruer et tracer l'Azimuth le plus Oriental, et ensuitte le plus Occidental de quelque Etoile fixe de celles qui passent entre le Pole et le Zenith, et diuisant apres cela par le milieu l'angle que font ces deux Azimuths sur ledit plan horizontal par une ligne droite, ce sera la meridienne.

Cette obseruation se peut faire commodement en une nuit dans l'espace de 6 ou 7 heures, et les Etoiles qui y sont les propres pour la latitude de Paris, qui est enuiron de 49 degrés⁶⁾, sont au mois de Mars et d'Avril, les 7 grandes etoiles de l'Ourse, exceptè celle qui est la dernière dans la queüe, parce qu'elle passe au dela du Zenit,

3) Voyez ce que nous disons à la p. 18 de l'Avertissement sur les dispositifs micrométriques.

4) En 1666 on était encore convaincu, paraît-il, de l'insensibilité, ou de la nullité, des réfractions pour des hauteurs supérieures à 30^o pour les étoiles, à 45^o pour le soleil. C'est du moins ce que dit J.D. Cassini, le contemporain de Huygens, à la p. 37 de son article ‘De l'origine et des progrès de l'astronomie, et de son usage dans la géographie et dans la navigation’. Comparez les notes 28 et 29 de la p. 15 de l'Avertissement qui précède.

5) Comparez la Fig. 3 de Huygens de la p. 30 qui suit. Comme la méthode d'observer ‘avec des silets’ fut déjà pratiquée par Huygens en ou vers 1658 (Fig. 3 de la p. 530 du T. XV), il paraît fort possible qu' Auzout marche ici sur ses traces. La Pièce d'Auzout pourrait donc (comparez la note 1 qui précède) être postérieure en date à la Pièce de Huygens qui constitue le § 4 qui suit.

6) Latitude de Paris et hauteur du pôle à Paris sont une et même chose. Il faut noter que la question de savoir si la terre est parfaitement sphérique ne se posait pas encore pour Auzout en 1666. Voyez sur la hauteur du pôle à Paris d'après Huygens et d'après Cassini la note 4 de la p. 266 du T. XIX. Mais consultez aussi la p. 17 de l'Avertissement qui précède et la Pièce Ia qui suit.

[p. 27]

vers la fin d'Aoust une Etoile a l'Epaule droite de Cephée, et uers le commencement de Novembre trois ou quatre Etoilles de Cassiopée.

Le brouillon de 1666 de cette Pièce se trouve à la p. 99 du Manuscrit C. Voyez la partie E bis de l'Appendîce II qui suit (p. 45).

§ 3. P. 5 et 6. Description de l'Equerre Azimuthale. Son usage pour trouver la ligne méridienne. M. Buot. ‘C'est une regle de Cuivre’, etc. Figure par Couplet⁷⁾.

§ 4. P. 7-10. M. Hugens. Pour trouuer l'ascension droitte des etoiles fixes. Il faut mesurer par le moyen d'une horloge a pendule le temps depuis qu'une Etoile fixe a passé par le Meridien iusqu'a ce que le soleil y passe le iour ensuiuant en comptant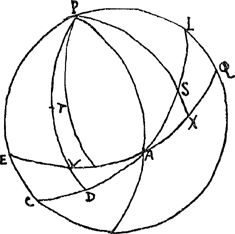

[Fig. 1]

par heures d'Etoiles; outre cela il faut prendre la hauteur meridienne du soleil en mesme temps, et 6 semaines, ou 2 ou 3 mois apres faire toutes les mesmes observations, remarquant comme auparauant le temps du passage par le meridien depuis l'etoile susdite iusqu'au soleil, que si l'etoile ne se peut obseruer commodement, on prendra quelque autre dont la difference ascensionelle d'auec la premiere soit connüe.

Ces observations faites l'on en deduira l'ascension droite requise comme s'ensuit.

Soit EPQ [Fig. 1] le meridien de la Sphere, l'Equateur EQ, le Pole P, l'Eclyptique LC, le commencement d'Aries A. Supposons qu'a la première observation le lieu du soleil dans l'Eclyptique ait esté en S, et la seconde fois en L, et soit mené par le Pole et par S le grand cercle PSX coupant l'Equateur en X. Que l'etoile observée et dont on cherche l'ascension droite soit T par laquelle soit aussy mené du Pole le grand cercle PV coupant l'Equateur en V et soit PA le Colure des Equinoxes. Donc par le temps qui est entre le passage de l'Etoille T et celuy du soleil S par le meridien, dans la premiere observation l'on scaura l'angle SPT et semblablement dans la derniere l'on scaura l'angle LPT, duquel ostant SPT restera connu l'angle SPL. Or par les observations des hauteurs Meridiennes du soleil, et par la connoissance de la hauteur du Pole, l'on a aussy les costés

7) Voyez sur Buot et Couplet la note 8 de la p. 89 du T. XIX.

[p. 28]

PS, PL du triangle PSL; l'on connoistera donc par le calcul son angle S qui est egal a l'angle S du triangle ASX duquel estant aussy connu le costé SX et l'angle X droit, l'on scaura par le calcul le costé AX qui mesure l'angle APX lequel osté de TPX qui estoit connu, restera APV qui osté de 360 degrés le reste sera l'ascension droite de l'Etoile T, d'ou l'on connoistera aussy celle des autres fixes par les differences des ascensions droites trouuées auparauant.

C'est dans le ‘§ 5’ qui suit qu'il est question de la détermination des différences des ascensions droites des étoiles. Nous aurions donc pu intervertir les §§ 4 et 5; mais nous avons préféré nous en tenir à l'ordre des Registres. Voyez toutefois sur ce sujet l'Appendice II qui suit.

L'on pouuoit aussy faire le Calcul du triangle PSA au lieu de celuy de ASX pour trouuer l'angle SPA, et l'un et l'autre donnera aussy le costé AS, qui est la longitude du soleil a la derniere observation; item l'on connoistera l'angle SAX qui est l'obliquitè de l'Eclyptique.

§ 5. Maniere de trouuer les lieux des etoiles fixes, par le moyen d'une horloge a pendule & de filets, comme aussy leur refraction. Premierement pour trouuer les Ascensions droites ou pour mieux dire leurs differences, l'on n'aura qu'a suspendre deux filets auec des poids en bas, a la distance de 7. ou 8. pieds (ou d'auantage selon la commodité du lieu) en sorte qu'ils se rencontrent precisément dans le plan du meridien. Ce qui estant fait, et l'horloge estant ajustée a la longueur des iours des etoilles qui sont plus courts que les iours moyens solaires de 3 min. 56 sec., l'on obseruera quand chaque étoile arriuera dans ledit plan du meridien determiné par les 2. filets, et l'on fera regarder au mesme instant quelle heure, minute et seconde marque l'horloge.

Connoissant par ce moyen le temps entre le passage de 2. Etoiles et comptant pour chaque heure 15. degrés, l'on aura la difference de leurs ascensions droittes.

L'on se peut aussy servir de l'horloge a cet usage sans qu'elle soit ajustée a la longueur des iours des etoiles ny mesme aux solaires; car en attendant seulement iusqua la nuit prochaine ou 2. ou 3. autres apres, et prenant garde a quelle heure de l'horloge une des estoiles obseruées retourne dans le plan du meridien, l'on connoistera par la combien l'horloge va trop viste ou trop lentement; et suiuant cela l'on reduira aisement les interualles du temps qu'on auoit marqué selon l'horloge aux interualles veritables pour en conclure la difference des ascensions droites comme dessus.

Pour trouver ensuitte la declinaison des mesmes etoiles l'on suspendera un troisieme filet, en sorte que le Plan qui passe par cettuycy, et par celuy des autres filets qui est du costé de l'Oeil fasse un angle connu avec le plan du meridien [Fig. 3]; l'on fera par exemple cet angle de 60. degres ou plus ou moins comme on le iugera meilleur pour la certitude de l'operation, et il n'importe pas que ledit Angle soit pris du costé d'Orient ou d'Occident a l'égard du plan du Meridien.

L'on obseruera apres cela le passage de chaque etoile par le dernier plan incliné a celuy du midy faisant regarder au mesme instant quelle heure marque l'horloge, et les

[p. 29]

mesmes etoiles estant aussy obseruées quand elles ont passé par le plan du midy, ou quand elles y passeront, l'on scaura le temps que chacune employe au passage entre lesdits deux plans. Par lequel et par la hauteur du Pole donnée l'on trouuera leur declinaison ainsy que s'ensuit.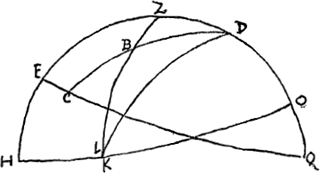

[Fig. 2]

Soit HZO [Fig. 2] le meridien du lieu de l'Obseruation, HO, l'horizon, P le Pole, EQ l'Equateur, Z le zenit, ZK le Cercle Vertical qui decline du meridien d'autant qu'est l'angle susdit determiné par les trois filets par ex. de 60 degrés et posons que l'Etoile B ait esté obseruée premierement dans l'Azimut ZK à 9 heures du soir, et qu'a 11. heures elle se soit trouuée dans le meridien HZO, ou il faut noter que je suppose l'horloge ajustée aux iours des Etoiles.

Soit mené par le Pole et par l'Etoile B un grand cercle coupant l'Equateur en C.

Dans le triangle spherique BZP l'on connoist l'angle BPZ qui est de 30. degrés a cause que l'Etoile a passé en 2. heures du Cercle PC a celuy du Meridien HZO. De plus l'angle BZP est donné estant le complement a 2. droits de l'angle HZK qui a esté supposé de 60. degrés. Et enfin le costé ZP est aussy donné estant le complement de la hauteur du Pole. L'on trouuera donc aussy le costé PB et partant son complement au 90. degré BC, ou bien l'excès dont il les surpasse, dont l'une ou l'autre seront la declinaison boreale ou australe de l'Etoile B.

Que si outre les filets perpendiculaires qui sont icy representés par AB, CD, EF [Fig. 3], l'on en adiouste d'autres horizontaux ou a peu pres qui ioignent les filets AB aux autres CD, EF comme font icy les filets GK, GH, AC, AE, dont les deux premiers doiuent estre un peu plus distans de terre que de la hauteur d'un homme, il n'y a point d'etoile visible sur nostre horizon dont on ne trouue la situation par cette voye pourveu que l'on etablisse l'angle HZK [Fig. 2] qui est celuy que comprennent les plans des filets perpendiculaires en sorte que l'angle B du triangle BZP soit de grandeur mediocre.

Au reste il est a noter qu'en cette methode il n'est causé aucun inconuenient par la refraction de l'Atmosphere, parce qu'une etoile estant veüe dans le plan du meridien

[p. 30]

ou de quelque Azimuth l'on scait asseurement qu'elle y est veritablement, et que la refraction peut seulement la faire paroistre plus haute.

Par consequent cette mesme maniere peut aussy seruir a trouuer la refraction des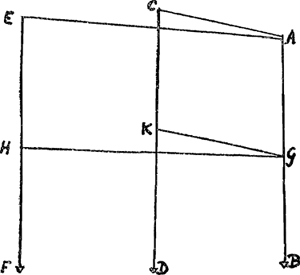

[Fig. 3]

etoiles, si lorsqu'elles arriuent au plan de l'Azimuth susdit ZK, l'on prend leur hauteur apparente. Car par le calcul du triangle BZP estant connu le costé ZB, dont le complement est la veritable hauteur de l'Estoile B, l'on aura en l'ostant de la hauteur obseruée la quantité de la refraction de ladite Etoile dans cette Elevation sur l'horizon.

§ 6. P. 10-12. M. Auzout proposa une reflexion qu'il auoit faite a laquelle il ne voioit pas qu'aucun astronome eust songé qui estoit que quand on prend le diametre de la Lune, il faut necessairement auoir egard a sa hauteur qu'elle a sur l'horizon ... ‘quand elle est a l'horizon elle est presque plus eloignée de l'Oeil de l'Observateur du diametre de la terre que si elle passoit au zenith’

Comparez les calculs de Huygens de la fin de 1666 sur la distance de la lune qui constituent la partie A de l'Appendice III qui suit.

§ 7. P. 13 et suiv. M. de Roberval. Méthode pour trouuer la Parallaxe de la Lune⁸⁾; et autres sujets.

8) Nous observons que d'après Delambre (‘Histoire de l'Astronomie moderne’ T. II, p. 259-260) Roberval et Fl. de Beaune avaient été, longtemps avant la création de l'Académie, amis de Morin qui leur avait communiqué sa méthode de mesurer les parallaxes, après quoi ils cherchèrent l'un et l'autre de leur côté la solution du problème.

[p. 31]

§ 8. P. 18-19. M. Hugens. Pour trouuer la refraction de l'Atmosphere a l'esgard du soleil. Il faut supposer que le soleil n'a point de parallaxe sensible comme l'on a assés reconnu par l'Experience.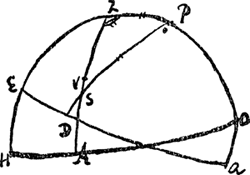

[Fig. 4]

Soit maintenant HZO [Fig. 4] le meridien, HO l'horizon, Z le zenith, P le Pole. EQ l'Equateur. V le soleil obserué, c'est-à-dire auec refraction, et son azimuth ZVA et que S dans le mesme Azimuth soit le lieu du soleil, ou il paroistroit sans refraction, et soit mené un grand cercle SP.

L'on obseruera donc la hauteur du soleil AV, et au mesme instant on remarquera l'heure qu'il est sur une horloge a pendule qui auparauant aura esté ajustée au soleil. Par cette heure l'on connoistra premierement l'angle P du triangle PZS, et en second lieu aussy le costé PS. qui est le complement de la declinaison du soleil. Mais outre cela le costé PZ est aussy connu, estant le complement de la hauteur du Pole. Partant l'on trouuera facilement le costé ZS duquel ostant ZV qui est le complement de la hauteur du soleil obseruée, l'on aura VS la quantité de la refraction a cette hauteur la.

Autrement. Pour trouuer la mesme chose sans l'aide d'une horloge a pendule l'on prendra en mesme temps la hauteur du soleil AV [Fig. 4], et l'arc AH entre son Azimuth et le meridien ou l'angle Z du triangle SZP sera donné. Or le costé PS est connu a peu prés estant le complement de la declinaison du soleil au iour de l'obseruation mais a une heure inconnüe et le costé ZP est connu precisement. Partant l'on trouuera a peu pres l'angle ZPS, et l'on scaura par la à peu pres quelle heure il estoit au temps de l'Obseruation, par laquelle on rectifiera ensuitte la declinaison du soleil, et l'on la connoistra auec autant de precision qu'il est besoin. L'on scaura donc aussy son complement SP, et estant connu PZ et l'angle PZS, l'on trouuera ensuitte aussy le costé ZS du triangle PZS, et ayant osté ZV qui est connu par l'observation de ZS, l'on aura l'arc de la refraction VS qu'il falloit trouuer.

§ 9. P. 20-28. Obseruation de l'Eclypse du Soleil du 2^e Juillet 1666, faite dans la maison de M^r. Colbert. Par M^rs. Hugens, de Carcauy, Roberual, Auzout, Frenicle et Buot.

C'est la Pièce publiée dans le T. VI que nous avons mentionnée aussi dans l'Avertissement qui précède.

[p. 32]

§ 10. P. 28-30. M. Picard. Obseruations des Diametres des Planetes en 1666. ‘Le 26^e Novembre au soir Saturne parut selon son grand Diametre de 40′ et selon l'autre de 16′’ ... ... Picard donne aussi les diamètres de Jupiter, de Mars, de Vénus et de la Lune. La dernière observation est du 10 décembre 1666.

En 1659 Huygens avait trouvé 68″ pour le diamètre apparent de Saturne (en son périgée). La valeur de Picard (40″) est meilleure⁹⁾.

§ 11. P. 30-33. [Huygens]. Comme la construction de tables exactes du mouuement des astres est une des principales choses que l'on se propose dans l'astronomie .. .. etc. Voyez la Pièce II qui occupe les p. 258-263 du T. XIX. Huygens vante e.a. (p. 263) la précision que nous donnent les horloges a pendule et dit en terminant que la création d'un observatoire muni de grands et bons instruments¹⁰⁾ donnera ‘tout suiet de se promettre un heureux succes de ce que l'on entreprendra.’

§ 12. P. 33. Auzout traite des méthodes pour mesurer la grandeur de la terre.

§ 13. P. 37. M. Auzout. ‘Memoire des Instrumens & autres choses necessaires dont il faudra fournir ceux qui iront à Madagascar’¹¹⁾.

‘Deux grands quarts de Cercle’ .... ‘Deux bons pendules a secondes, ou l'un a secondes, et l'autre a demisecondes. Une machine de M. Hugens pour les demisecondes, si elle reussit mieux que les pendules ordinaires. Et si l'on veut faire l'Epreuve des longitudes par le moyen des pendules de mer de M. Hugens il faudra deux de ces pendules dans le Vaisseau. Plusieurs boules de Cuivre rondes pour faire en toutte occasion des pendules a secondes, demisecondes &c.’

Auzout mentionne ensuite non seulement les lunettes, mais aussi les instruments et ingrédients nécessaires pour fabriquer et polir des lentilles, e.a. ‘une suffisante quantitè de morceaux de bon verre bien choisy’; ainsi que ‘la machine pour se seruir des Lunetes sans tuiau’. Voyez sur ce dernier sujet la p. 19 de l'Avertissement qui précède.

Il parle aussi des ‘thermometres’¹²⁾ et des ‘barometres’¹³⁾. Puis e.a. de ‘plusieurs tuyaux de verre ou sarbacanes tant pour les instruments nommés que pour faire les niveaux de M. Tevenot’¹⁴⁾; de ‘deux machines pour sonder la profondeur de la mer et pour puiser l'eau du fond de la mer¹⁵⁾; des ‘tables Rudolfines, de Bouillaud et de Riccioli’¹⁶⁾, d'‘un livre de navigation, comme l'hydrographie du P. Fournier¹⁷⁾, d'un ‘horloger capable de faire (?) et de racommoder les Instruments’.

9) Voyez la note 3 de la p. 343 du T. XV.

10) La construction de l'Observatoire se termina en 1672.

11) Cette expédition a été mentionnée e.a. aux p. 9 et 10 du T. XVIII.

12) Voyez les p. 257 et 345 du T. XIX.

13) P. 257 du T. XIX.

14) Consultez sur Melchisédec Thévenot la note 5 de la p. 370 du T. I. Il devint membre de l'Académie Royale des Sciences en 1685. Sa collection ‘Veteres Mathematici’ parut à Paris en 1693, un an après sa mort. Voyez sur son niveau, datant de 1661, les p. 105-108 qui suivent où Huygens en parle avec éloges. Il ne s'agit pas d'un niveau servant au nivellement comme celui de Huygens (p. 81-104 qui suivent), mais d'un instrument ‘à mettre une surface plane parallele a l'horizon’.

15) Voyez sur ce sujet la note 8 de la p. 143 du T. XIX.

16) Comparez la note 10 de la p. 261 du T. XIX.

17) Voyez sur cet ouvrage les p. 200-201 du T. XVII.

[p. 33]

Comme l'Appendice II qui suit le fait voir, les brouillons des Pièces précédentes de Huygens (§§ 2, 4, 5, 8) sont de 1666 (note 1 de la p. 43). Or, le § 13 qui précède date du 11 janvier 1667 d'après la p. 155 du T. II des Registres. On dirait donc, d'après l'une et l'autre donnée, que les Pièces antèrieures au § 13 constituent des discussions ou communications à l'Académie datant de 1666. On trouve toutefois dans le dit T. II encore les remarques qui suivent:

P. 157. Le 23 février [1667] ... M^rs Hugens et Roberval ont proposé leur Methode qui est de prendre devant et apres l'Equinoxe la hauteur meridiene du soleil et sa declinaison, par ce moyen et par les parties proportionnelles on aura le temps de l'Equinoxe, puis on prendra la nuict la hauteur meridienne d'une etoille: et ainsy on aura la distance de l'étoille du poinct de l'Equinoxe.

P. 158. Monsieur Hugens donnera la maniere de trouuer le lieu des estoilles fixes sans auoir egard a l'Equinoxe.

Monsieur Hugens a proposé une autre methode par le moyen de la pendule en prenant le temps qui est entre le Meridien du Soleil, et celuy de l'Etoille, ou la difference du temps qui est depuis que le Soleil a passé par le meridien jusques a ce que l'Estoille y passe.

P. 159. Mons^r. Hugens a donné une Methode pour trouuer les Ascensions droites des etoilles fixes.

Aux p. 159-160 on trouve les dates du 23 mars et du 30 mars.

P. 161. Monsieur Hugens a esté d'auis que pour bien regler le mouuement de la Lune, il faut scavoir exactement l'Equation du temps, d'autant que Ptolomée, Kepler et les autres Astronomes y ont fait beaucoup de sautes¹⁸⁾.

18) Voyez les l. 2-3 de la p. 123 du T. XVII (Ptolemaei error et Copernici’, remarque de Huygens de 1660); notre note en cet endroit (dans cette note 10 le lecteur est renvoyé e.a. aux p. 523 et 547 du T. III; il y a ici une faute d'impression; au lieu de T. III il faut lire T. XV)renvoie à d'autres passages des Tomes précédents. Voyez sur Kepler la p. 17 du T. III; il semble d'ailleurs possible qu'au lieu de Kepler il faille lire Copernic: comparez la p. 318 qui suit.