Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 547]
| |
V. À propos de la méthode du marquis de l'hospitalGa naar voetnoot1).
| |
[pagina 548]
| |
On peut dans la construction mettre 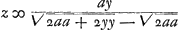 .
Huygens a trouvé cette valeur en égalant deux expressions de la soustangente: .
Huygens a trouvé cette valeur en égalant deux expressions de la soustangente: 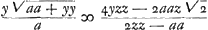 tout en ayant aussi égard à l'équation de la courbe 2yzz ∞ aay + 2aaz √2. Vérification de cette valeur de z: tout en ayant aussi égard à l'équation de la courbe 2yzz ∞ aay + 2aaz √2. Vérification de cette valeur de z:
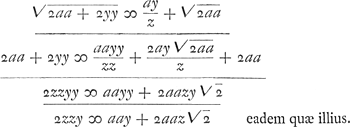
§ 2. Construction de Mr. le Marquis de l'Hospital pour trouver la longueur d'une partie donnée de la ligne Logarithmique. En marge: Cette construction suppose qu'on sache la soutangente generale de la Logarithmique, qu'on ne scauroit trouver. Et pour decrire cette courbe qui conviene a une soutangente donnée, on ne le peut qu'en supposant la quadrature de l'hyperbole. Soit la Courbe Logarithmique indefinie ABCD [Fig. 129], qui a pour asymptote la droite TE. D'un point quelconque E de cette asymptote ayant menè la perpendiculaire EL, soit decrite la courbe Geometrique HI, dont la nature soit exprimée par cette Equation (EF ou EG ∞ y. FI ou HG ∞ z) 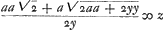
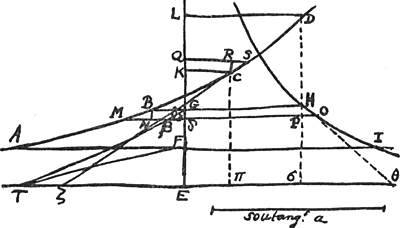 [Fig. 129]
Cette figure est une copie, avec quelques additions, de celle de l'Hospital (T. X, p. 314). | |
[pagina 549]
| |
Ou, en ostant les incommensurables, aay + 2aaz √2 ∞ 2yzz. Que l'on mene à present deux paralleles quelconques AFI, BGH à l'asymptote TE. Et ayant pris TE ∞ a, parametre ou soutangente; EL ∞ FI; EK ∞ GH; et menè les droites TG, TF, et les paralleles LD, KC qui rencontrent la Logarithmique aux points D, C; je dis que la portion AB de cette Logarithmique est egale à TG - TF + LD - KC. Demonstration. Ayant pris l'arc BM infiniment petit, et menè MO parallele à BH, l'on nommera, comme fait Monsr. Leibnitz, BN ou HP,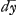 ; MN ; MN 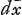 : et l'on aura par la proprieté de la Logarithmique dx ∞ ady/y, d'où l'on tire BM ou : et l'on aura par la proprieté de la Logarithmique dx ∞ ady/y, d'où l'on tire BM ou 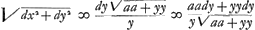 : or il est clair que la somme des : or il est clair que la somme des 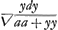 dans la portion AB ∞ TG - TF. de sorte qu'il ne reste plus qu'a demontrer, que la somme des dans la portion AB ∞ TG - TF. de sorte qu'il ne reste plus qu'a demontrer, que la somme des 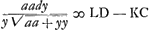 : ce que je prouve ainsi. Soit prise KQ ∞ OP, et soit menée QS. l'on trouvera par la Methode des Tangentes de Barrou ou de Mr. Leibnitz, que OP ou : ce que je prouve ainsi. Soit prise KQ ∞ OP, et soit menée QS. l'on trouvera par la Methode des Tangentes de Barrou ou de Mr. Leibnitz, que OP ou 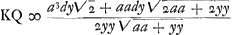 . Or par la proprietè de la Logarithmique . Or par la proprietè de la Logarithmique 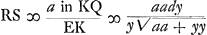 . Donc la somme des RS c'est à dire LD - KC ∞ à la somme des . Donc la somme des RS c'est à dire LD - KC ∞ à la somme des 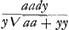 dans la portion AB. Donc &c.
Ayant examinè cette Construction et Demonstration, je les ay trouvè bonnes, et l'invention admirablement belle et subtile. Voir pag. 99, 100, 101, 102, 103, item 160Ga naar voetnoot3) ou est ma solution. Il aura trouvè que la construction de la courbe dont dans la portion AB. Donc &c.
Ayant examinè cette Construction et Demonstration, je les ay trouvè bonnes, et l'invention admirablement belle et subtile. Voir pag. 99, 100, 101, 102, 103, item 160Ga naar voetnoot3) ou est ma solution. Il aura trouvè que la construction de la courbe dont 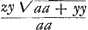 est soutangente, dependoit de la quadrature de l'hyperbole, et qu'ainsi on la peut construire par le moien de la Logarithmique. Or elle sera reduite a la quadrature de l'hyperbole, si la quadrature de la courbe θθxxaa + θθx4 ∞ a6 se reduit a celle de l'hyperbole. est soutangente, dependoit de la quadrature de l'hyperbole, et qu'ainsi on la peut construire par le moien de la Logarithmique. Or elle sera reduite a la quadrature de l'hyperbole, si la quadrature de la courbe θθxxaa + θθx4 ∞ a6 se reduit a celle de l'hyperbole.
En marge: Au lieu de dy je mets λ, au lieu de dx je mets ϰ, ce qui est plus commode. Comparez à la p. 509 qui précède le § 1 ter de la Pièce III (theorema Barrovij). En marge: Notez que parce que ET ∞ a, il s'en suit que GT est parallele a celle qui toucheroit la courbe en B, et qu'ainsi Gβ est egale et parallele à BM. d'ou il | |
[pagina 550]
| |
paroit que menant δθ perpendiculaire sur Gβ, sa partie Gθ sera 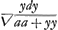 . Et on voit aisement que la somme de toutes cellecy sera ∞ TG - TF. . Et on voit aisement que la somme de toutes cellecy sera ∞ TG - TF.
Voyez en outre sur la rectification de la logarithmique l'article de Huygens publié dans la livraison de février 1693 de l'‘Histoire de Ouvrages des Sçavans’ (T. X, No. 2793, à la p. 407) que nous citons aussi à la fin de la Pièce VI qui suit. |
|


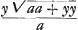 appartenoit la courbe 2yzz ∞ aay + 2aaz √2? J'ay eu de la peine a prouver que cela est ainsi. Je le prouve en tirant de cette courbe la soutangente par la regle des Tangentes, vient
appartenoit la courbe 2yzz ∞ aay + 2aaz √2? J'ay eu de la peine a prouver que cela est ainsi. Je le prouve en tirant de cette courbe la soutangente par la regle des Tangentes, vient 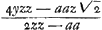 , qui doit estre la mesme que
, qui doit estre la mesme que 