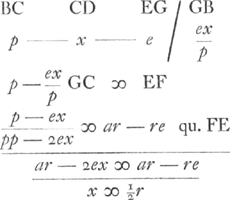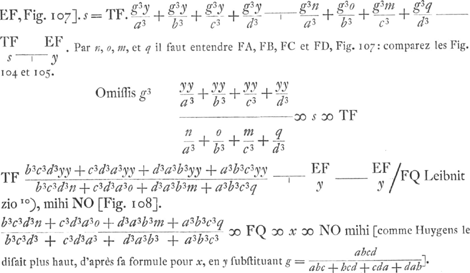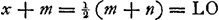Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 491]
| |||
I. Fatio de Duillier et Huygens. Méthode des tangentes pour les ‘Curvae filares’ de Tschirnhaus, ou plutôt pour les courbes données en coördonnees bipolaires, tripolaires etc., les poles ici considerés étant situés sur une droite.
| |||
[pagina 492]
| |||
court grand risque d'estre fausse. Cependant ce qu'il avoir trouvè de la somme egale des sinus, servoit a demontrer facilement le Theoreme susdit du centre de gravité, et estoit fort beau. Voiez à la page precedente [c.à.d. le § 2 qui suit]. 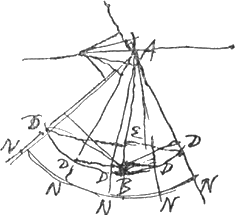 [Fig. 99]
Il avoit trouvè le centre de gravitè de tous les points N [Fig. 99], puis il considera que la somme des perpendiculaires tirées d'un point de la ligne AB si elle estoit perpendiculaire a la tangente, devoit estre egale d'un et autre costè de cette ligne. En suite il crut que ces distances depuis les centres de gravitè des fils au point B estant egales d'un costè et d'autre, cela ne convenoit pas au centre de gravitè. Mais s'il avoit menè des points D des sinus sur AB, il auroit vu qu'ils estoient chacun egaux perpendiculaires de B sur les lignes AN, et qu'ainsi AB estoit le vray axe de pesanteur des fils.
Après le 17 mars Huygens resta en communication avec Fatio de D.: on lit au bas de la feuille: prestè le reçeuil des Journaux de 1685 [il s'agit sans doute du Journal des Scavans ou peut-être aussi des Acta Eruditorum] à M.r Duilliers 20 Mars 1687. | |||
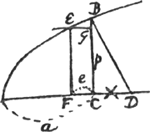
§ 2Ga naar voetnoot2).A, B, C [Fig. 100] puncta data in linea recta vel utcunque. KDK curva ejusmodi naturae ut ductis ad ejus punctum quodlibet rectis AD, BD, CD. harum summa sit datae rectae aequalis.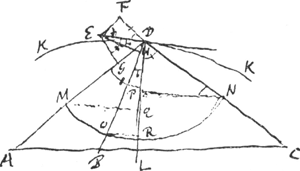 [Fig. 100]
quaeritur tangens in D. Sit ea DE, et E punctum proximum D. idque censendum in curva existere. Ab E in rectas AD, BD, CD, si opus est productas, cadant perpendiculares EG, EH, EF. Ergo si ex A, B, C ducerentur rectae ad E, crescet ea quae ex C longitudine DF, | |||
[pagina 493]
| |||
quae ex B diminuetur longitudine DH, quae ex A diminuetur item longitudine DG. Ergo ut summa ductarum ex A, B C, ad E sit aequalis tribus ex A, B, C ad D ductis, hoc est rectae datae, oportet DF aequari duabus DH, DG. Sit tangenti DE perpendicularis DL, et ex D descripta circumferentia secet rectas AD, BD, CD in M, O, N. unde ducantur in DL perpendiculares MQ, OR, NP. Quod si jam pro radio circuli sumatur DE, apparet angulorum DEF, DEH, DEG esse sinus DF, DH, DG. Istis autem angulis aequales sunt singulis singuli PDN, RDO QDM, quorum sinus sunt NP, OR, MQ. Ergo sicut sinus DF aequatur duobus DH, DG, ita sinus NP aequabitur duobus OR, MQ. Unde facile colligitur punctorum M, O, N centrum gravitatis esse in recta DL. Itaque reperto hoc centro, dabitur recta DL, quae tangenti DE est ad angulos rectos. Eadem vero est constructio quotcunque data fuerint puncta [unde rectae] ad D ducendae quarum summa sit data. | |||
§ 3Ga naar voetnoot3). Ratio inveniendarum tangentium in curvis lineis.Ponitur CD [Fig. 101] esse tangens quaesita in puncto C. in ea proximè puncto C,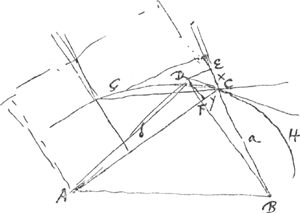 [Fig. 101]
accipi intelligitur punctum D. quod idem in curva proposita esse censetur. Ex D cadant perpendiculares in AC et BC, nempe DF, DE. Recta AC superare censetur | |||
[pagina 494]
| |||
rectam AD differentiâ FC quia DF minima respectu AF. Item BD superare censetur rectam BC, differentia CE. CE vocatur x. CF, y. quarum si inter se ratio cognoscatur, dabitur D punctum in concursu perpendicularium ED, FD. adeoque tangens CD. Ista vero ratio investigatur ex aequatione in qua ponitur parte una proprietas curvae lineis datis AC, CB expressa; parte altera eadem proprietas expressa lineis AD, BD, seu pro ijs AF, EB. Vel tantummodo exprimatur proprietas curvae positis a + x et b - y pro a et b. et deleantur omnia praeterquam in quibus unum x aut y. Ut deleantur etiam in quibus x et y conjunctim. Reliqua dabunt rationem x ad y ac proinde tangentis constructionem. | |||
§ 4.Proprietas curvae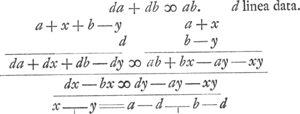 | |||
§ 5.Proprietas curvae ut | |||
§ 6.Les §§ 6 et 7 sortent du cadre de la Pièce I: il ne s'agit pas ici de coördonnées bipolaires (ou tripolaires etc.), mais de coördonnées cartésiennes orthogonales; a et b sont les coördonnées courantes, x et y leurs accroissements. Le rapport y : x détermine la direction de la tangente.
Parabola [Fig. 102]. r latus rectum. 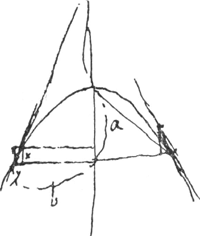 [Fig. 102]
 | |||
§ 7.In circulo. 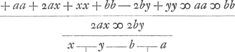 | |||
[pagina 495]
| |||
§ 8Ga naar voetnoot4).HO perpend. in tangentem HK [Fig. 103]. Hic NT ponitur ∞ x. Puisque d + c = const. (d'après les équations qui suivent) il s'agit ici de l'ellipse. 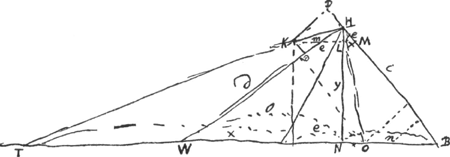 [Fig. 103]
 | |||
[pagina 496]
| |||
§ 9Ga naar voetnoot5)Les équations qui suivent font voir qu'ici le produit cd des deux rayons vecteurs est par hypothèse constant. Il s'agit donc de la courbe qui plus tard recevra le nom de lemniscate.
Omittuntur in quibus plura e quam unum. 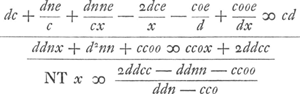 Atqui cc - nn ∞ pp atque etiam dd - oo ∞ pp. Huygens désigne donc maintenant pa p ce qui dans la Fig. 103 s'appelle y, et dans la Fig. 104 s'appellera p. 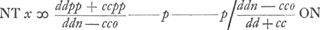 N.B. quod hic [c.à.d. dans les facteurs c + ne/c etc. et d - oe/d etc.] in numeratoribus nullum x. et unum e vel nullum. et in denominatoribus tantum unum x. Cumque in aequatione tantum scribenda sunt in quibus unum e vel nullum, hinc fit ut, sive quadrata inventarum linearum sive cubi sive rectangula ex duabus, vel solida ex tribus, efficienda sint, semper tamen simplex x aequale proditurum sit quantitati cognitae. | |||
§ 10Ga naar voetnoot5).Le calcul suivant s'applique à la Fig. 104. Le résultat est le même que celui obtenu dans le § 9: ce qui plus haut s'appelait ON est maintenant désigné par BF ou x. 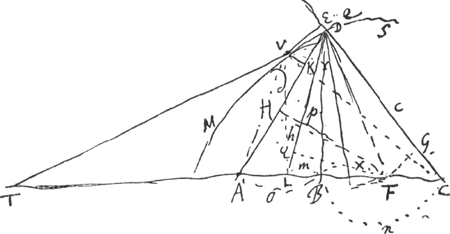 [Fig. 104]
| |||
[pagina 497]
| |||
Proprietas curvae MDS, ut semper ▭ duarum ex C et A punctis ad ipsam ductarum eidem spatio qq aequale sit. 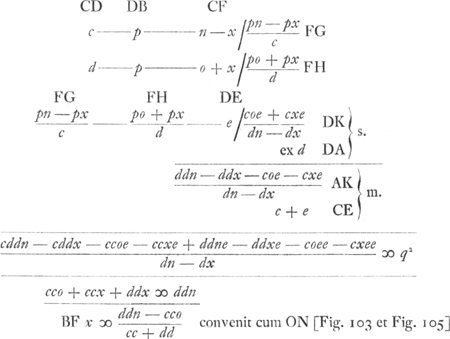 | |||
§ 11Ga naar voetnoot6).Hoc modo optimè et brevissimè ad aequationem pervenitur [Fig. 105]. Idem hic modus est qui in fine paginae praecedentis [§ 10]. 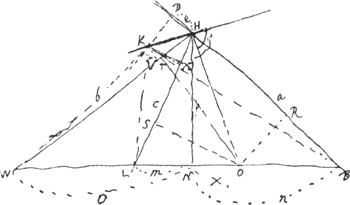 [Fig. 105]
| |||
[pagina 498]
| |||
 KHD et ∆ HOS simile KHX ut facile apparet propter angulum rectum OHK. nam HO ponitur perpend. in tangentem HK. 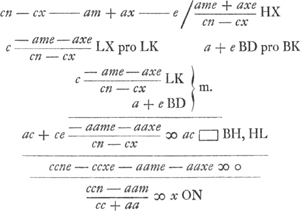 ON [ou plutôt BF] ex pag. ante praecedentem 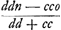 convenit cum hac ON (d pro c, c pro a, o pro m), sed hic facilius invenitur. convenit cum hac ON (d pro c, c pro a, o pro m), sed hic facilius invenitur.
| |||
§ 12.Cas où la courbe considérée est déterminée par la constance de la somme des deux rayons vecteurs c et d: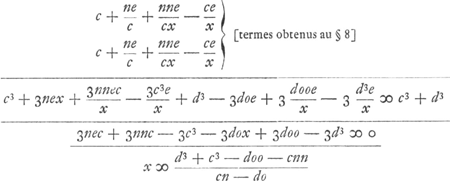
| |||
[pagina 499]
| |||
Sed dd - oo ∞ pp, cc - nn ∞ pp NT 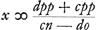 [Fig. 103 où toutefois p s'appelait y] [Fig. 103 où toutefois p s'appelait y]
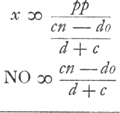 | |||
§ 13.Proprietas ut solidum trium rectarum à punctis B, L, W [Fig. 105] ad curvae punctum ductarum, semper eidem solido aequale sit. Solidum d3 ∞ acb. 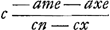 LX pro LK [voyez le § 11]. LX pro LK [voyez le § 11]. 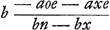 WV pro WK. a + e BD pro BK. WV pro WK. a + e BD pro BK.
C'est de ces formules que Huygens sera usage dans le Manuscrit G en considérant la première ovale de Descartes; voyez, à la p. 463 qui précède, la Pièce IV des ‘Mathematica varia 1681-1695’.  | |||
§ 14.Proprietas ut summa quadratorum ab L et B punctis [Fig. 105] ad curvam inclinatarum sit semper eidem spatio aequalis. 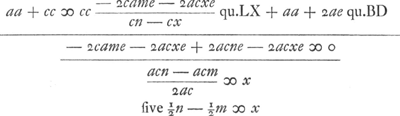 hic curva fit circuli circumferentiaGa naar voetnoot7). | |||
[pagina 500]
| |||
§ 16Ga naar voetnoot9).Natura curvae EE [Fig. 107] est haec ut sit abcd/g ∞ abc + bcd + cda + dab [AE = a, BE = b, CE = c, DE = d]. EQ perpend. tangenti ET. 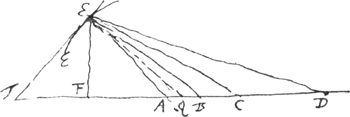 [Fig. 107]
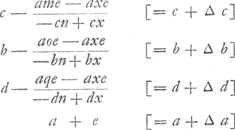 Voyez les §§ 11 et 13 qui précèdent sur ces expressions qui représentent les accroissements [∆a, ∆b, ∆c, ∆d] des quatre rayons vecteurs lorsqu'on passe du point H au point K [Fig. 108]. HK est donc un élément de la courbe et en même temps de la tangente. HO ⟂ HK est la normale à la courbe au point H. | |||
[pagina 501]
| |||
Huygens écrit que l'accroissement de abcd/g (g étant apparemment une constante), lorsqu'on
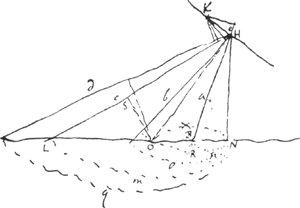 [Fig. 108]
passe du point H au point K, est égal à celui de abc + bcd + cda + dah. En effectuant la multiplication [c + ∆c] [b + ∆b] [d + ∆d][a + ∆a], où il néglige les termes contenant e à un degré supérieur au premier, en retranchant ensuite cbda de ce premier produit, et en divisant finalement par g, il trouve ce que nous appelons 1/g ∆ (abcd), accroissement de abcd/g. De la même manière il trouve ∆ (abc) etc. L'équation 1/g ∆ (abcd) = ∆ (abc + bcd + cda + dab) permet, après division par e, de trouver l'inconnue x. Huygens obtient 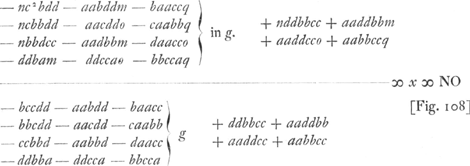 Si restituatur valor g qui est 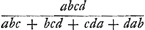 fit x hic idem quod QF Leibnitzio pag. sequenti [Fig. 107]. fit x hic idem quod QF Leibnitzio pag. sequenti [Fig. 107].
Constructio Leibnit zij [il s'agit - voyez la note 30 de la p. 486 - de la construction indiquée dans le tableau du No 2214, T. VIII, p. 269, Leibniz à Huygens, 26 janvier 1680]. y = GF [lisez | |||
[pagina 502]
| |||
§ 17.Les ‘curvae filares’ (expression de Huygens) considérées par Tschirnhaus ne sont pas exclusivement celles où les fils sont tendus par des points matériels (ou plutôt, pour fixer les idées, par des stylets linéaires perpendiculaires au papier) demeurant tous en repos à l'exception de celui dont la pointe trace la courbe: ils peuvent également être tendus par des courbes convexes fixes et rigides situées, comme les points fixes, dans le plan du papier ou, si l'on préfère cette expression, dans le plan de la ‘curva filaris’. Le passage suivant du Manuscrit GGa naar voetnoot11), ou plutôt la Fig. 109 à laquelle il se rapporte, fait bien voir, lorsqu'on considère A comme un point lumineux, le rapport existant entre des courbes ainsi construites et certaines catacaustiquesGa naar voetnoot12). 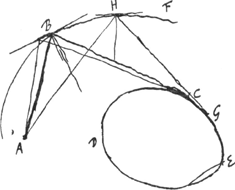 [Fig. 109]
Si ABCE sit filum, defixum in A puncto et ambiens curvam CEGa naar voetnoot13). Eoque semper tenso describatur curva BF. Ostendendum rectas AB, BC curvae BF vel rectae ipsam tangenti in B, aequalibus angulis occurrere. Ostendendum deinde expuncto B non posse exire nisi unam curvam ut BHFGa naar voetnoot14), ita comparatam ut ducta a puncto ejus aliquo H recta AH, et HG tangente curvae CE, utraque AH, HG occurant curvae BHF angulis aequalibus. Haec Do. Tchirnhaus demonstranda sunt. Nous avons déjà fait mention en termes généraux de ce théorème de Tschirnhaus à la p. 483 de l'Avertissement qui précède. Or comme Tschirnhaus l'affirme, le théorème - dont il ne | |||
[pagina 503]
| |||
donne pas la démonstration disant qu'elle serait très longueGa naar voetnoot13) - est correct quoique Huygens semble ne pas en avoir trouvé la preuve, sans doute faute d'y réfléchir sérieusement. Il sussit, pour en faire voir la vérité, de remplacer la courbe fixe par un polygone. Dans le cas de la Fig. 109 bis la ‘curva filaris’ BH se compose de deux (etc.) arcs d'ellipse se raccordant au point P et dont le
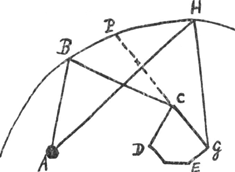 [Fig. 109 bis]
premier a pour foyers les points A et C, le deuxième les points A et G. Il est donc évident que la tangente est perpendiculaire, d'abord à la bissectrice de l'angle ABC, ensuite à celle de l'angle AHG. Or, ceci reste vrai, quelque grand que soit le nombre des côtés du polygone; l'on peut être assuré qu'il en sera encore de même à la limite lorsque le polygone, pour nous exprimer ainsi, devient une courbe. Comparez sur les démonstrations de ce genre les notes 1 de la p. 388, 4 de la p. 401 et 9 de la p. 403 du T. XVIII. Notre démonstration reste valable lorsque, comme dans certaines figures de Tschirnhaus, le point fixe A est remplacé lui aussi par une courbe convexe fixe. Il est de plus évident que dans le cas de la Fig. 109 bis, et par conséquent aussi dans celui de la Fig. 109, il n'y a, lorsque le point B est donné (de même que le point A et le polygone, ou la courbe fixe) qu'une seule courbe continue BPH capable de concentrer la lumière réfléchie successivement en C, en G, en E etc., précisément celle qui se compose des arcs d'ellipse dont nous avons parlé. Nous observons encore qu'on a dans la Fig. 109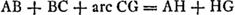 , ce qui peut conduire dans certains cas à la rectification de la courbe fixe (ou catacaustique). Tschirnhaus se vante de posséder une méthode fort générale pour la rectification des courbes. Dans le cas p.e. de la réflexion de rayons parallèles sur une circonférence de cercle (du côté concave), ce qui est le cas considéré en 1678 par Huygens (T. XVIII, p. 399), ainsi qu'en 1690 dans le Traité de la Lumière (T. XIX, p. 537) et, en mars 1691, à la p. 73 du T. X, on a, dans la figure de cette p. 73, arc , ce qui peut conduire dans certains cas à la rectification de la courbe fixe (ou catacaustique). Tschirnhaus se vante de posséder une méthode fort générale pour la rectification des courbes. Dans le cas p.e. de la réflexion de rayons parallèles sur une circonférence de cercle (du côté concave), ce qui est le cas considéré en 1678 par Huygens (T. XVIII, p. 399), ainsi qu'en 1690 dans le Traité de la Lumière (T. XIX, p. 537) et, en mars 1691, à la p. 73 du T. X, on a, dans la figure de cette p. 73, arc 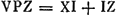 , donc ‘tota VME = 3/2 AN’ conformément au prêsent théorème de Tschirnhaus: le point lumineux (A) de la présente Fig. 109 se trouve alors à l'infini, les points B et H de la Fig. 109 sont les points V et I, ou V et A, de la figure de la dite p. 73Ga naar voetnoot15). , donc ‘tota VME = 3/2 AN’ conformément au prêsent théorème de Tschirnhaus: le point lumineux (A) de la présente Fig. 109 se trouve alors à l'infini, les points B et H de la Fig. 109 sont les points V et I, ou V et A, de la figure de la dite p. 73Ga naar voetnoot15).
| |||
[pagina 504]
| |||
Nous avons publié un facsimilé de la p. 48r du Manuscrit G, où se trouve la Fig. 109, dans notre article - comparez la p. 594 qui suit - ‘Deux pages consécutives du Manuscrit G de Chr. Huygens’ inséré dans la revue ‘Janus’, organe de la société historique néerlandaise des sciences médicales, exactes et naturelles, 1e à 3e livraisons janvier-mars 1940Ga naar voetnoot*. On trouve dans le même article la Fig. 109 bis et le facsimilé de la p. 47v du Manuscrit contenant les définitions du corps, de la surface, de la ligne et du point sur laquelle on peut consulter les p. 190 et suiv. qui précèdent. À cet article fait suite un deuxième article - voyez également la p. 594 qui suit - intitulé ‘Démonstration mécanique des théorèmes de Tschirnhaus considérés dans le T. XX des Oeuvres Complètes de Chr. Huygens’ (Janus, 7e à 9e livraisons juillet - septembre 1940). Nous y disons être d'avis que Huygens n'aurait pas récusé cette démonstration: voyez (T. XVII, p. 286) ce qu'il dit en 1659 sur la méthode mécanique d'Archimède servant à démontrer une ou des propositions géométriques et consultez aussi sur la Méthode d'Archimède dont il s'inspirait parfois lui-même la note 5 de la p. 553 qui suit. |
|