Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 445]
| |
Mathematica varia 1681-1695. | |
[pagina 447]
| |
Avertissement.Des dix Pièces qui suivent la plupart se rapportent à des questions de géométrie; c'est ce que le lecteur eût assurément deviné d'avance. Une Pièce (II) traite de trigonométrie, une (IV) de géométrie analytique (équation d'une courbe), trois (I, VI, X) de rayons de courbures, trois aussi (V, VII, IX) d'intégration, plus précisément du calcul de la grandeur de certaines surfaces ou de certains corps obtenus par la révolution de lignes ou de surfaces. Une seule (III), publiée dans le T. XIV, se rapporte au calcul des chances (comparez les Mathematica varia 1666-1681), une autre (VIII) à celui des logarithmes en partant de la considération de l'hyperbole équilatère et en faisant usage d'une certaine série trouvée par Huygens et publiée par lui en 1690 dans le ‘Discours de la cause de la pesanteur’Ga naar voetnoot1).
On a remarqué dans les Math. varia 1666-1681 les problèmes assez nombreux sur le triangle, sujet cher à tant de mathématiciens anciens et modernes; Huygens s'y servait d'équations en x et y de sorte qu'il s'agissait, peut-on dire, de géométrie analytique. Quant aux formules trigonométriques, la présente Pièce II fait voir que Huygens aimait à trouver lui-même leurs démonstrations plutôt que de les chercher ailleurs. Le catalogue de vente de 1695 de ses livres ne mentionne pas la ‘Mirifici Logarithmorum Canonis Descriptio’ de 1614 de NeperGa naar voetnoot2) dans le Livre II de laquelleGa naar voetnoot3) l'auteur considère e.a. longuement le cas où ‘sunt ... tria latera [trianguli sphaerici] data, & quaeruntur anguli’. Huygens trouvait apparemment les énoncés des différents | |
[pagina 448]
| |
théorèmes dans les petites tables, celles in octavo, de VlacqGa naar voetnoot4). Or tant dans l'édition latine que dans les deux éditions néerlandaises que nous citons Vlacq dit en latin ou en flamand: ‘Qui demonstrationes hujus videre cupiunt - mais c'est ce que Huygens ne désirait pas - eas invenient in Trigonometria Britannicâ Henrici Briggii’.
Dans la Pièce de géométrie analytique (IV) datant de 1690 Huygens considère une des ovales de DescartesGa naar voetnoot5). Nous rappelons qu'au commencement de cette année il avait publié le ‘Traité de la Lumière’Ga naar voetnoot6) dans le Chap. VI duquel il est également question de ces ovalesGa naar voetnoot7).
Tout ce qui se rapporte à des développées et des rayons de courbure (Pièces I, VI, X) se rattache évidemment à la Troisième Partie de l'‘Horologium oscillatorium’ de 1673Ga naar voetnoot8).
Des recherches sur les surfaces et corps de révolution (Pièces V, VII, IX) nous ne mentionnons ici que la dernière, où il est question tant de la cissoïde que de la cycloïde, ce qui donne lieu à Huygens de rappeler les ‘profondes speculations’ de Pafcal et de WallisGa naar voetnoot9).
La Pièce fur le calcul des logarithmes se rattache à un endroit des ‘Principia’ de 1687 de Newton, ainsi qu'à la quadrature de l'hyperbole par Mercator et Wallis, comme le font voir les notes des p. 471-472 ou plutôt les pages des T. IX et X auxquelles ces notes renvoient le lecteur. Nous terminons cet Avertissement en disant un mot du développement du cofinus en une série, sujet dont il est question dans la Pièce I. Dans la note 6 de la p. 392 qui précède on trouve la série de Newton 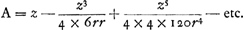 . .
| |
[pagina 449]
| |
ou, en divisant par 2r et en posant ½z = s,  , ce qui est le développement de ce que nous appelons le sinus (sin s dans la formule est une ligne, non pas un rapport) en fonction de l'angle correspondant (s = arc, r = rayon). Wallis cite également, ce que nous n'avons pas reproduit dans la note, le développement du sinus versus suivant Newton, savoir , ce qui est le développement de ce que nous appelons le sinus (sin s dans la formule est une ligne, non pas un rapport) en fonction de l'angle correspondant (s = arc, r = rayon). Wallis cite également, ce que nous n'avons pas reproduit dans la note, le développement du sinus versus suivant Newton, savoir  .
Or, en retranchant le sinus versus du rayon, on obtient le cosinus (c.à.d. le cosinus linéaire, analogue au sinus linéaire mentionné plus haut); en divisant par r il en résulte le développement de ce que nous appelons aujourd'hui le cosinus: .
Or, en retranchant le sinus versus du rayon, on obtient le cosinus (c.à.d. le cosinus linéaire, analogue au sinus linéaire mentionné plus haut); en divisant par r il en résulte le développement de ce que nous appelons aujourd'hui le cosinus:
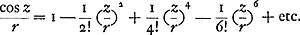
C'est depuis l'apparition de l'Algèbre de 1685 de Wallis que Huygens a connu ce développement en série du cosinus. Il ne connaissait d'ailleurs pas la preuve des formules de Newton, et il ne paraît pas s'en être jamais servi. En 1683 il ne les connaissait certainement pas encore. On a vu plus hautGa naar voetnoot10) que la série de l'arc tangente de J. Gregory lui était même inconnue au moins jusqu'à 1689. Il ne semble pas étonnant qu'après sa dispute avec GregoryGa naar voetnoot11) on n'ait pas éprouvé en Angleterre le besoin, supposé qu'on l'eût éprouvé sinon, de lui faire connaître au plus tôt les nouvelles découvertes. Mais pour la considération théorique du ‘pendulum cylindricum trichordon’ (1683), dont traite la Pièce IGa naar voetnoot12), il n'avait que faire de développements en série. |
|

