Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 420]

V.
Principe des ondes-enveloppes. Courbes diacaustiques.

Lame de verre servant à concentrer en un point donné unfaisceauderayons convergeant vers un autre point.
Rayons courbés dans le cas de la réfraction atmosphérique.
[1676 ou 1677.]⁶⁾

[Fig. 142.]

[Fig. 143.]

§ 1.

La Fig. 142 fait voir les surfaces d'ondes dans le cas de la réfraction; comparez la Fig. 130 de la p. 408. La Fig. 143 représente les surfaces d'onde dans le cas des lames minces, ainsi que les ‘anneaux de Newton’ que Huygens avait d'ailleurs déjà observés avant lui (en 1665, T. XVII, p. 268 et 341-348).

6) Manuscrit E, p. 81-83. Voyez sur la date la note 1 de la p. 416.

[p. 421]

§ 2.

Les rayons concentriques qui sortent du verre par la surface plane inférieure VM forment dans l'air la courbe diacaustique VHN.

VM [Fig. 144] superficies vitri versus K. Radij tendunt ad punctum P et in exitu franguntur. fractis tangens communis curva VHN.

Curva NHV aequatur NM + 3/2 MK.

Nam cum K undae VK pervenit in M, simul V venit in Q ut VQ sit ∞ 3/2 KM. Sed MR undae pars. Ergo reliqua pars undae est RQ. Sed RM est ex evolutione partis curvae RN, et RQ ex evolutione partis reliquae RV. Ergo NR + RV sive curva tota aequalis NM plus VQ, sive NM + 3/2 MK.

§ 3.

Les rayons concentriques qui, en sortant de l'air, pénètrent dans le verre limité par la surface plane BC y forment la courbe diacaustique EF.

DC ⫟ CE ut 2 ad 3 [Fig. 145]⁷⁾.

DA ∞ DB.

BF tangens curvae factâ BS ∞ 3/2 BD.

Erit curva FE + recta EC + 2/3 CA ∞ rectae BF

ablataque GB ∞ EC + 2/3 CA, fiet curva EF ∞ rectae GF.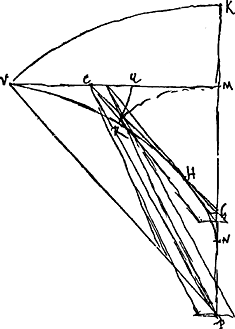

[Fig. 144.]

[Fig. 145.]

7) Le rayon réfracté que provient d'un rayon se dirigeant vers D et faisant avec l'axe AD un angle infiniment petit, coupe cet axe en un point E tel que CE : CD = n (indice de réfraction); ou, pour mieux dire, E est la limite vers laquelle tend l'intersection du rayon réfracté avec l'axe, lorsque l'angle du rayon incident avec l'axe devient plus qu'une valeur donnée quelconque.

[p. 422]

§ 4. Curva omnium undarum particularium tangens communis erit propagatio undae principalis intra vitrum [Fig. 146]. Ergo rectae quae hanc curvam tangentem communem secant ad angulos rectos, erunt radij refracti. Hi autem aliunde dantur. Ergo hi ipsi curvam illam secant ad angulos rectos. Ergo curva oritur ex evolutione curvae alterius quae tangens communis est horum radiorum.

Sufficit scire quod undae intra vitrum propagantur per istas rectas. Sed cum debeant rectae secare undas ad angulos rectos, mirum videri posset quomodo lineae non ad unum centrum tendentes, undas secare possint semper ad angulos rectos. At hoc jam explicatur per evolutionem.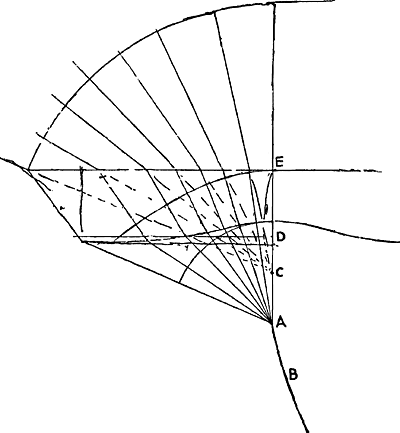

[Fig. 146.]

[p. 423]

La courbe AB de la Fig. 146 est de même nature que la courbe EF du § précédent: c'est l'enveloppe des rayons réfractés dans le verre. On voit aussi dans la figure, dans la lame comme ailleurs, les trajectoires orthogonales des rayons: ce sont des intersections de surfaces d'ondes avec le plan de la figure. Avant de parvenir à la diacaustique les rayons rencontrent la surface inférieure de la lame de verre courbée de telle manière qu'après la traversée ils redeviennent concentriques. Huygens ne donne pas l'équation en coördonnées cartésiennes de la courbe méridiane de la surface inférieure. On peut écrire, comme il l'indique, que tous les rayons, e.a. celui qui se meut suivant l'axe EDCA, employent le même temps pour parvenir à partir d'une surface d'onde sphérique située dans l'air au-dessus de la lame jusqu'au point de concentration A: comparez les Pièces VI et X qui suivent.

Huygens avait l'intention de publier dans son Traité le cas considéré dans ce paragraphe, mais il biffa plus tard le paragraphe de la ‘Première copie’ qui s'y rapporte.

§ 5. La Fig. 147 est le prototype de la première figure du Chap. IV (‘De la Refraction de l'air’) du Traité de la Lumière.

Voyez sur les rayons courbés la p. 392 de l'Avertissement.

[Fig. 147.]