Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695
(1937)–Christiaan Huygens–
[pagina 77]
| |
Dynamique. | |
[pagina 79]
| |
Avertissement.A la fin du premier Avertissement de ce Tome nous avons dit (p. 9) que quoique Huygens soit atomiste, les forces admises par tout-le-monde, telles que les tensions des cordes ou celles exercées par les dents d'une roue, jouent un grand rôle, dans ses écrits. Ce qui était vrai pour les Pièces relatives à la Statique qui précèdent, l'est également pour les Pièces sur la Dynamique qui suivent. On n'y trouve rien sur la constitution moléculaire des corps. En particulier Huygens ne tâche pas d'expliquer la grandeur de la résistance qu'un mobile éprouve dans l'eau ou dans l'air par la considération des particules qui constituent ces milieux, comme Newton devait le faire, d'ailleurs sans rien affirmer, dans son ouvrage de 1687Ga naar voetnoot1). Comme Huygens le dira en 1691Ga naar voetnoot2) la résistance du milieu est pour lui ‘comme une pression, qui est comparée à celle de la pesanteur’. ‘À Mr. Newton et à moy la resistence est la pression du milieu contre la surface d'un corps, etc.’ Apparemment les forces dont il est question dans la dynamique sont de même nature que celles que considère la statique: là aussi | |
[pagina 80]
| |
toutes les forces pouvaient suivant Huygens être comparées à la pesanteur (p. 16 et 27 qui précèdent). Le § 1 de la Pièce de 1668 qui suit dit clairement (p. 104) que la ‘vis gravitatis’ et la ‘resistentia aeris’ sont, pour un corps, ou plutôt pour un point matériel, lancé verticalement en l'air, des ‘causae retardationis’ pareilles. L'air, soufflant de bas en haut contre un globe en repos, ou traversé par un globe tombant verticalement, lui enlève une partie de son poids (p. 106). Pour tout corps punctiforme donné, c'est le fondement du calcul de la Pièce IV ainsi que de la Pièce VI, l'accélération ou la retardation dans le sens du mouvement, est proportionnelle à la force agissant dans cette directionGa naar voetnoot1). Dans le cas d'une résistance proportionnelle à la vitesse du mobile (Pièce IV) le mouvement d'un globe lancé obliquement résulte donc (p. 113, note 13) de la composition des mouvements horizontal et vertical, les vitesses initiales de ces mouvements étant les composantes de la vitesse initiale donnéeGa naar voetnoot2).
A propos du fondement mentionné, il importe de remarquer que Huygens ne parle qu'incidemment de la question de savoir si les principes de la mécanique - voir sur les principes la p. 697 du T. XVIII, ainsi que la p. 16 qui précède (principe des déplacements virtuels ou vitesses virtuelles) - peuvent être démontrés par raison. Voyez les p. 166 et 171 qui suivent où il parle en 1668 d' ‘un effet de la nature, qui ne s'estant pû jusqu'icyGa naar voetnoot3) demonstrer par raison mais seulement prouver par experience, doit estre pris pour principe’Ga naar voetnoot4). Voyez aussi à la p. 164 le § 4 de la Pièce X, où il dit en 1686 que ‘[Leibniz] ne peut pas pretendre qu'on luy accorde ce principe de la conservation de la force motrice comme qui n'auroit pas besoin de preuve’, en quoi d'ailleurs Leibniz (inspiré par les résultats obtenus par Huygens, voir le § 3 de la Pièce X, et le dernier alinéa de la note 6 de la p. 359 du T. XVI) imitait plus ou moins Descartes (§ 1 de la même Pièce), lequel suivant Huygens (mais non pas suivant le sentiment que Leibniz lui attribue) dérive ‘cette [fausse] loy de la nature qu'il s'y conserve constamment la mesme quantitè de mouvement ...... immediatement de l'immutabilitè de Dieu’. Nous avons vu qu'en 1693 (T. XVIII, p. 471, dernier alinéa, et p. 477, note 1, T. XIX, p. 7-9) Huygens s'est pourtant résolu à considérer | |
[pagina 81]
| |
la thèse que ‘nihil virium perditur aut interit nisi effectu edito et exstante ad quem producendum tantundem virium requiritur quantum est id quod decessit’ comme un axiome. Il faut bien qu'il y ait des axiomes: ‘nisi principium ponatur nihil demonstrari potest’ T. XVI, p. 114).
Bientôt après avoir considéré géométriquement le mouvement d'un corps dans le cas d'une résistance proportionnelle à la vitesse, Huygens apprit par les expériences de 1669 (Pièce V) que la résistance est plutôt proportionnelle au carré de la vitesse. Il en tira la conclusion (p. 107, note 14) que sa spéculation de 1668 était ‘falsa, licet pulcherrima’. Mais il est permis de dire que la question de la méthode a ici plus d'importance que celle de la conformité avec l'expérience. On peut dire de ces paragraphes, ce que Huygens disait en 1691 (T. X, p. 23) seulement à propos de ses calculs de 1669 complétés plus tard, où la résistance est prise proportionnelle au carré de la vitesse (Pièce VI), savoir que la ‘ratio inveniendi’ est telle que son ‘utilitas ad alia quoque pertinet’. Même vers 1691 Huygens ne publia d'ailleurs point sa ‘ratio inveniendi’ (T. X, p. 23-45). En 1690, talonné par la publication de Newton (Principia, Lib. II), il publia sans preuves dans l'‘Addition’ au ‘Discours de la Cause de la Pesanteur’ les résultats obtenus en 1668 et 1669. A-t-il en 1668 et dans les années suivantes gardé sa première Pièce pour lui-même sans en causer avec qui que te fûtGa naar voetnoot5)? C'est ce qu'il est impossible de savoir. En 1669 (fin du § 10 de la Pièce VB, à la p. 142) il parla à l'Académie d'un ‘traité particulier’ qu'il pourrait consacrer à ces recherches. Les constructions et calculs de 1669 sont cependant certainement restés à l'état de brouillonsGa naar voetnoot6). Quant à ceux de 1668, un peu moins confus, les mots ‘hinc incipienda demonstratio’ et ‘faciendae propositiones plures ut huc veniatur’ (p. 118) indiquent qu'il se proposait de les mieux rédiger, mais après 1669 il n'a apparemment plus été question de ce projet. Et nous ne trouvons pas dans les Registres qu'il en ait rien communiqué à l'Académie, ce qui, il est | |
[pagina 82]
| |
vrai, n'est pas absolument probantGa naar voetnoot1). S'il en avait causé à Paris avec Leibniz, il le lui aurait sans doute rappelé, ou bien Leibniz l'aurait dit, lorsqu'en 1690 et 1691 (T. IX, p. 367 etc., T. X, p. 18 etc.) les deux savants correspondaient sur ce sujet; et il paraît assez probable que si Leibniz avait vu, en tout ou en partie, la Pièce de Huygens, il aurait donné au mot ‘résistance’ le même sens que ce dernier. D'autre part en parlant de Newton - il observe p.e. (T. IX, p. 367) que ‘Mr. Newton [a traité de la résistance] plus amplement que pas un de nous deux’ - Huygens ne dit nulle part que Newton pourrait avoir appris quelque chose de ses recherches de 1668. Il nous semble donc probable qu'il a fait un mystère de la Pièce de 1668Ga naar voetnoot2); à cela près qu'il a annoncé à Oldenburg le 13 novembre 1668 (T. VI, p. 276) qu'il s'était occupé de la théorie ‘de la cheute .... tant sans la resistance qu'avec la resistance de l'air’. Il est toutefois certain que Huygens conversait avec Leibniz sur des questions mathématiques pendant que ce dernier séjournait à Paris, c.à.d. depuis 1672. Voyez p.e. la note 12 de la p. 244 du T. VIIGa naar voetnoot3), et consultez aussi les notes 12 de la p. 147, 4 de la p. 149, 12 de la p. 151 et 3 de la p. 152 qui suivent. Vers 1673 Huygens peut fort bien lui avoir donné quelque vague idée de sa méthode de 1668; or, c'est, peut-on dire, d'une méthode des fluxions que Huygens se sert dans les considérations géométriques sur l'accélération, la vitesse et le chemin parcouru qui nous occupent: le temps s'écoule évidemment sans discontinuité. Il est vrai que dans son ‘Historia et Origo Calculi Differentialis’ Leibniz indique, d'après la note nommée du T. VII, que lors de son séjour de quelques semaines à Londres en 1673Ga naar voetnoot4) il était trop peu versé dans la Géométrie pour avoir pu s'intéresser à la méthode des fluxions. Huygens ne se sert pas du mot ‘fluxus’ ou du verbe ‘fluere’, comme Neper et Cavalieri. Le seul nom qui se trouve dans la Pièce de 1668 (§ 3) est celui de Galilée.
Au sujet de cette Pièce nous devons faire ici quelques brèves remarques de nature mathématique. | |
[pagina 83]
| |
1o. Nous disons dans la note 19 de la p. 107 que Huygens admit à bon droit, que la courbe qui représente l'accélération du corps en fonction du tempsGa naar voetnoot5) est nécessairement une logarithmique, dès qu'il eut découvert que l'espace compris entre l'axe des temps, deux ordonnées perpendiculaires à cet axe et la courbe est proportionnel à la différence de ces ordonnées. Il le remarqua d'abord pour un espace infinitésimal; en concluant de là à l'existence de la même relation pour des espaces finis on peut dire qu'il intégra une équation différentielle, quoique l'‘aequatio differentialis’ ne fît son apparition que plus tard: voyez la note 7 de la p. 101. Nous parlons (brevitatis causa) des équations différentielles du mouvement qui se rapportent au problème de 1668 dans les notes 18 de la p. 107 et 4 de la p. 111. Rien n'est plus aisé aujourd'hui que d'obtenir par intégration, comme on l'a fait depuis longtemps, de l'équation 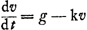 , s'appliquant à la chute verticale, ou , s'appliquant à la chute verticale, ou 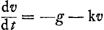 , se rapportant à l'ascension (la résistance étant proportionnelle à la vitesse), la vitesse - voir le No 3 qui suit - et ensuite le chemin parcouru en fonction du temps, partant la hauteur atteinte par le projectile et le temps qu'il met à monter et à redescendre. Or, il est clair que, dans cette intégration, le
mouvement est entièrement déterminé par l'équation différentielle, dès que la vitesse initiale est donnée. Puisqu'il s'agit d'un problème physique, il est parfaitement permis d'admettre à-priori que la vitesse initiale étant donnée, le mouvement doit être entièrement déterminé. Ayant trouvé une courbe capable de représenter le mouvement, Huygens pouvait donc en conclure sans hésiter que c'était là la solution unique. , se rapportant à l'ascension (la résistance étant proportionnelle à la vitesse), la vitesse - voir le No 3 qui suit - et ensuite le chemin parcouru en fonction du temps, partant la hauteur atteinte par le projectile et le temps qu'il met à monter et à redescendre. Or, il est clair que, dans cette intégration, le
mouvement est entièrement déterminé par l'équation différentielle, dès que la vitesse initiale est donnée. Puisqu'il s'agit d'un problème physique, il est parfaitement permis d'admettre à-priori que la vitesse initiale étant donnée, le mouvement doit être entièrement déterminé. Ayant trouvé une courbe capable de représenter le mouvement, Huygens pouvait donc en conclure sans hésiter que c'était là la solution unique.
2o. Après avoir expliqué pourquoi on obtient une logarithmique dans le cas de la chute verticale (p. 107, note 19), Huygens ne prend pas la peine de dire pourquoi il en est de même dans le cas de l'ascension. Les équations différentielles écrites ci-dessus font voir que dans le cas de la chute la vitesse v est proportionnelle à (g - dv/dt), c.à.d. dans la Fig 56 de la p. 108, l'espace ABOP à (OT - OP) ou PT; d'où il suit que la courbe AHP est une logarithmique. Or, dans le cas de l'ascension la vitesse est | |
[pagina 84]
| |
proportionnelle à (- dv/dt - g), c.à.d. dans la Fig. 54 de la p. 102, l'espace GFDE à (GF - GH) ou HF; d'où se tire la même conclusion. Sachant que AFDI est une logarithmique, on peut alors donner à la figure une deuxième interprétation. 3o. Une même logarithmique, considérée à partir du même point, est prise par Huygens (p. 107, note 19, Fig. 55) pour la descente comme pour l'ascension; dans le cas de l'ascension les vitesses (deuxième interprétation de la figure) sont situées à droite, dans le cas de la descente elles sont situées à gauche de la courbe; pour un même temps à partir du commencement de l'ascension ou de la descente la somme des deux vitesses est donc constante, bien entendu en prenant dans le cas de la descente une unité de vitesse deux fois plus grandeGa naar voetnoot1). On voit le plus aisément qu'il en est ainsi en considérant que d'après les équations différentielles intégrées la vitesse est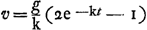 Ga naar voetnoot2) pour l'ascension et Ga naar voetnoot2) pour l'ascension et 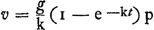 pour la descente. pour la descente.
Dans la Fig. 59 (p. 111, note 2) Huygens prend au contraire la même unité de vitesse partout. La courbe qui se rapporte à la descente se raccorde alors à celle qui représente l'ascension: la retardation, et par conséquent la direction de la tangente à l'un et l'autre arc, sont évidemment les mêmes pour la fin du mouvement ascendant et pour le commencement de la chute. 4o. Huygens ne donne (p. 118, note 3) la démonstration de sa construction de la courbe du jet que pour la Fig. 62 qui représente le cas particulier où le projectile est lancé en l'air sous un angle de 45o. Mais on voit aisément, en considérant le principe de cette démonstration, que dans le cas général elle est à peu près la même. Suivant les propositions du § 5 on a (Fig. 57) spat. AVE : spat. ADK = VS : DR et (Fig. 58) spat. ADL : spat. VDH = AM : VQ. Les espaces qui représentent des montées ou des descentes ∫ vdt (où les v, composantes verticales de la vitesse du projectile à différents moments, sont dans les figures des droites horizontales), peuvent, par des relations de ce genre, être transformés, à un facteur près, en des droites verticales. En plaçant ces dernières les unes à côté des autres de telle manière que leurs extré- | |
[pagina 85]
| |
mités inférieures se trouvent sur une même horizontale, p.e. à des distances égales (le mouvement horizontal est uniforme), on verra passer par leurs extrémités supérieures une courbe, qui se change en courbe du jet lorsqu'on multiplie toutes les ordonnées par un même facteur. 5o. Peu de lecteurs, sans doute, auront la patience d'examiner en détail les constructions géométriques de Huygens, remarque qui s'applique d'ailleurs à une grande partie de son oeuvre. Tout en admirant son ingéniosité, on conçoit bien, en jetant les yeux sur ces longueurs, que la recherche de méthodes plus efficientes s'imposait. Mais on voit aussi qu'une longue préparation est nécessaire, que les méthodes abrégées ne peuvent aucunement se présenter d'emblée à l'esprit humain.
Un trait caractéristique de l'esprit de Huygens, nous l'avons indiqué plusieurs fois, est le désir d'être aussi exact que possible, tant dans la construction d'instruments que dans les raisonnements mathématiquesGa naar voetnoot3). Sans doute, les instruments de précision qu'on possède aujourd'hui laissent fort loin derrière eux ceux du dix-septième siècle, et l'on peut dire la même chose à propos de l'exactitude des expériences modernes comparées à celles du temps de Huygens. Peu enclin en général à exécuter lui-même de longues séries d'expériences ou d'observations (comparez la note 17 de la p. 345 du T. XVII), Huygens a fait cependant quelques expériences - celles des Pièces XI et V qui suiventGa naar voetnoot4) - dont il dira plus tard (T. X, p. 19) qu'elles furent fort exactes. C'est ici surtout qu'il faut se rappeler que les écrits doivent être jugés d'après leur dateGa naar voetnoot5). Il y a parfois chez Huygens une légère tendance quelque peu antique, nous semble-t-il, à admettre sans raisons suffisantes la simplicité de la natureGa naar voetnoot6). Il dira | |
[pagina 86]
| |
(Pièce VB, § 3, au no 2) que si les résistances ne se montrent pas parfaitement proportionnelles aux carrés des vitesses ‘cela vient peut estre de quelque petit defaut qui s'est trouué dans l'experience’. Il parle de la ‘speculatio vera’ (p. 107, note 14) et dit (p. 142) qu'on pourra maintenant ‘determiner exactement ... la proportion des espaces que parcourent des corps pesants en tombant par l'air’.
Ce qui ressort avec évidence de la suite des Pièces IV, V et VI, c'est que les expériences de Huygens se rattachent aux questions théoriques qu'il considérait, et que d'autre part ses théories se rattachent aux expériences. Il s'était déjà occupé en 1646 et en 1659 de la chute à travers un milieu résistant (T. XI, p. 73; T. XVI, p. 384). En 1661 (T. III, p. 320) il est d'avis que ‘l'on ne pourra pas reduire [l'] accélération [d'une boule de liège] a quelque regle certaine’. Il connaissait les expériences de l'Accademia del Cimento, de Riccioli (T. V, p. 101, de 1664) et celles qu'on faisait en Angleterre (T. V, p. 355, de 1661; T. VI, p. 277, de novembre 1668; T. XVI, note 1 de la p. 344 et p. 356). On trouve à la p. 20 du Manuscrit B datant de 1661 la figure du parachutiste que nous mettons ici sous les yeux du lecteur; comparez sur la parachute en forme de ‘voile quarré’ la p. 142 qui suit. Une des causes immédiates de son travail d'octobre 1668 peut avoir été la lettre de Mariotte de février 1668 (T. VI, p. 177) qui venait de lire, sur l'avis de Huygens, les dialogues de Galilée et admet, comme ce dernier, que les corps tombants n'augmentent leur vitesse que ‘jusques a vn certain point’. En effet, Mariotte suppose ‘qu'vn vent soufflant de bas en haut puisse soustenir une boule de lieige’, ce qui est conforme à la considération de Huygens de la p. 106 (déjà citée à la p. 80). Les moulins (p. 140 qui suit; voyez aussi la note 5 de la p. 88) et les voiles des vaisseaux sont déjà mentionnés dans les programmes des p. 23 et 25 qui précè- | |
[pagina 87]
| |
dent. Il en est de même de la force mouvante de l'eau et de la vitesse de son écoulement. À la p. 142 qui suit il est question de la mesure de la profondeur de la mer suivant MersenneGa naar voetnoot1) (la Piece de Huygens de 1690 s'y rattache). Enfin - last not least - il faut se rappeler que dans le programme de la p. 23 Huygens mentionnait ‘ce qui regarde l'artillerie’. À la p. 80 nous avons parlé de ‘corps punctiformes’ ou de ‘globes’ lancés en l'air; mais les Fig. 61 et 63 font bien voir que dans la pensée de Huygens il s'agit en réalité de boulets ou de bombes. Les dialogues de Galilée eux aussi montrent que la détermination, exacte ou approchée, machina volansGa naar voetnoot6)
de la courbe du jet préoccupait surtout - comment en eût-il pu être autrement? - les princes et les capitainesGa naar voetnoot2). Déjà en 1646 (T. I, p. 34) Huygens connaissait fort bien les ‘Cogitata physicomathematica’ de 1644 de Mersenne, dont fait partie la ‘Ballistica’Ga naar voetnoot3). Personnellement il est animé, comme Mersenne, d'un esprit pacifiqueGa naar voetnoot4), et ce n'est certes pas dans des buts militaires qu'il s'intéresse à l'art de volerGa naar voetnoot5). À la figure du para chutiste nous ajoutons celle de l'avion mis en mouvement par deux hélices de la f. 33r du Manuscrit G (datant probablement de 1689), à laquelle Huygens joint des vers grecs indiquant qu'il s'agit d'un rêveGa naar voetnoot7):
ὑπνος ὁτε γλυϰιων μελιτος βλεφαροισιν ἐφιζων
λυσιμελης, πεδαα μαλαϰω ϰατα φαεα δεσμω.
| |
[pagina 88]
| |
Nous avons dit (T. XVIII, p. 486) ne pas savoir si les expériences de Huygens sur les cordes vibrantes furent prises chez lui ou à l'Académie. Il avait chez lui, c.à.d. à la Bibliothèque du Roi, d'après sa lettre du 3 décembre 1666 à son frère Lodewijk (T. X, p. 727), ‘une ... chambre .... ou [ses] instruments et machines [étaient] rangées’. Sans doute y-prenait-il des expériences avec ou sans CoupletGa naar voetnoot8) ou d'autres assistants. D'après les §§ 2 et 3 de la Pièce V il paraît que les expériences sur la force | |
[pagina 89]
| |
mouvante de l'air prises dans la cour de la Bibliothèque furent précédées, comme cela se conçoit, par la construction d'un modèle de l'appareil; sortant, pensons-nous, du domicile de Huygens.
Les Pièces II, III, VII, VIII et IX sont fort brèves. La Pièce II n'a de l'intérêt qu'au point de vue de la brièveté des formules. Dans la Pièce III on peut remarquer, comme partout ailleurs, que si Huygens désigne un temps, une vitesse, etc. par une lettre, c'est toujours après s'être figuré ce temps ou cette vitesse par une ligne droite (ou parfois par une surface, comme dans les Pièces IV et VI). On remarquera aussi dans la Pièce III la façon correcte dont Huygens prend en 1690, quoique sans se servir du symbole dx de Leibniz (p. 451 du T. IX), la différentielle d'un radical. La Pièce VII (mouvement roulant sur un plan incliné) a été écrite immédiatement après que Huygens eut trouvé le théorème que la force vive totale est la somme des forces vives du mouvement progressif et du mouvement de rotation autour du centre de gravité (T. XVIII, p. 433-436). Il résulte de ce théorème que le mouvement progressif est d'autant plus lent que le mouvement de rotation absorbe une plus grande partie de la force vive. Voyez sur le calcul des moments d'inertie les p. 419-426 du T. XVIII. La Pièce VIII indique que les tensions dans un corps tournant sont indépendantes du mouvement progressif considéré en cet endroit (principe de relativité pour les translations uniformes). La Pièce IX est de nature expérimentale; toutefois, il semble s'agir plutôt d'expériences projetées que d'expériences réelles. Si Huygens avait sérieusement expérimenté sur la collision de cylindres, il aurait sans doute constaté que les observations ne confirment pas toujours exactement sa théorie de la collision des corps durs (p. 8 qui précède): voir la note 11 de la p. 17 du T. XVI. Huygens parle ici de la ‘fistuca’ ou ‘festuca’, ce qui signifie le poids mobile d'un appareil pour enfoncer des pilotis (sonnette à déclic; en hollandais: heimachine, dérivé du verbe heien) comme on en voit souvent chez nous, aujourd'hui comme au dix-septième siècle. Nul n'ignore qu'Am- | |
[pagina 90]
| |
sterdam est bâtie sur des pilotis. On peut se figurer qu'il écrivit la Pièce après avoir vu une de ces machines à l'oeuvreGa naar voetnoot1). Voyez sur la question du travail la note 2 de la p. 160.
Dans leur ensemble ces petites Pièces font bien voir, avec les Pièces IV et VI, que Huygens envisageait la possibilité, lontaine sans doute, de donner de tous les phénomènes une explication mécanique correcte.
Il se trompe toutefois en admettant le 13 février 1669Ga naar voetnoot2) pour un jet non contractéGa naar voetnoot3) à la fois la loi de Torricelli sur l'écoulement de l'eau - à de petites différences prèsGa naar voetnoot4) - et la thèseGa naar voetnoot5) que la pression de l'eau sortant d'une ouverture est ‘egale a celle du poids du cylindre d'eau [nous désignons la hauteur par h] qui a l'ouverture pour base’; thèse qu'on trouve également chez Mariotte dans son ouvrage de 1686Ga naar voetnoot6) et dont Daniel Bernoulli dira en 1738Ga naar voetnoot7): ‘Huic sententiae plerique, imo omnes, adhaeserunt & adhaerent’Ga naar voetnoot8). En effet, l'eau qui tombe avec une vitesse v sur la platine immobile de la balance, lui donne par seconde une impulsion Sδv2, δ étant la densité de l'eau et S l'aire d'une section normale du jet, égale, dans la pensée de Huygens à l'ouverture. Ceci peut s'écrire 2δghS (g = accélération de la pesanteur) en admettant la loi de TorricelliGa naar voetnoot9). Or, d'après cette formule l'impulsion du jet équivaut à la pression d'un cylindre d'eau de section droite S et de hauteur 2h, c.à.d. deux fois plus haut que celui dont parle Huygens. Nous avons déjà dit à la p. 10 du T. XVI que la théorie de l'impulsion n'avait pas encore été établie. | |
[pagina 91]
| |
Trois jours plus tard, le 16 février 1669Ga naar voetnoot10), Huygens crut découvrir que la loi de Torricelli est parfois fort inexacte ‘ce qui n'estoit pas facile a deviner’: il constata que dans son expérience la quantité d'eau sortie de l'ouverture n'était que les deux tiers de celle à laquelle il s'était attendu, et comme il ne songeait apparemment pas à une contraction du jetGa naar voetnoot11), il conclua ‘que toute l'eau qui sort par le trou du vase n'a pas autant de vitesse qu'auroit un corps en tombant de la surface de l'eau’.
Quant à la thèse de Huygens du 13 février 1669 sur l'impulsion - thèse inexacte, nous l'avons dit, dans le cas d'un jet non contracté, et dont il n'avait pas tâché de donner une démonstration théorique - elle fut confirmée par les expériences du 3 avril 1669Ga naar voetnoot12). En réalité, cette confirmation était certainement due à la contraction du jet. M.J.M. BurgersGa naar voetnoot13) nous écrit: ‘La valeur du coëfficient α de contraction - rapport de la section droite du jet à l'ouverture - est une fonction des particularités de la forme du trou et dans une certaine mesure aussi de la forme du vase, particularités dont dépend la répartition des pressions et des sous-pressions sur les parois dans le voisinage immédiat du trou. Ce n'est que dans des cas exceptionnels que l'on peut calculer a priori la valeur de α. Des expériences ont montré que pour un trou circulaire bien aménagé dans une paroi mince on peut admettre α = 0,61 à 0,6Ga naar voetnoot14). Dans | |
[pagina 92]
| |
ce cas ou aurait 2δghS = environ 1,25 δghS. Pour des diamètres fort petits du trou cette valeur peut devenir encore plus petite par le frottement’Ga naar voetnoot1). Ainsi s'explique l'égalité approximative, dans les expériences du 3 avril, entre l'impulsion de l'eau et le poids du cylindre d'eau de volume hS, l'impulsion se montrant toutefois un peu plus grande.
Ceci fait bien voir qu'il ne faut accepter que cum grano salis les raisonnements et les conclusions de Huygens. On peut remarquer que, tandis que les forces exercées par l'eau qui s'écoule dans les conditions indiquées sont théoriquement proportionnelles au carré de la vitesse, il n'en est pas de même dans le cas d'un objet tiré par une corde à travers de l'‘eau immobile’Ga naar voetnoot2): la résistance dépend alors de la vitesse d'une façon fort compliquée bien que - nous citons de nouveau M. Burgers - ‘dans certaines conditions, par exemple pour des corps à des arêtes vives, des régimes se présentent dans lesquels la proportionnalité au carré de la vitesse se trouve réalisée’. Il est vrai que Huygens ne cherche pas à établir une théorie du phénomène; il ne fait qu'énoncer le résultat des expériences en disant ‘que les impressions de l'eau contre une mesme surface sont [approximativement] comme les quarrez des vitesses’Ga naar voetnoot3); mais en ajoutant ‘que la premiere experience qui pese l'impression de l'eau par la balance quand elle sera bien affermie est la plus assurée de toutes’, il établit peut-être un lien trop étroit entre les deux genres d'expériencesGa naar voetnoot4). Une remarque analogue s'applique aux expériences sur la force mouvante et la résistance de l'air. |
|

