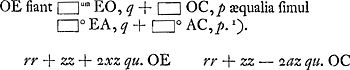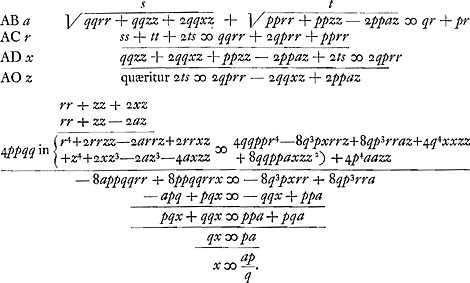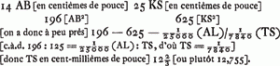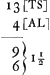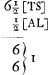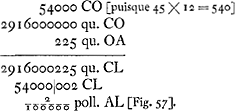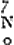VII B. § 3 (1665).
|
-
voetnoot1)
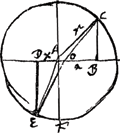
- Comparez sur ce calcul, emprunté à la p. 70 du Manuscrit B, la p. 266 de l'Avertissement qui précède. C'est la répétition d'un calcul de Fermat qui venait de retrouver la loi de Snellius ou de Descartes en partant du principe ancien qui fut précisé plus tard sous le nom de ‘principe de la moindre action’. Ici c'est d'un temps minimum qu'il s'agit; si l'on admet le principe, il suffit, pour trouver la loi de la réfraction, puisqu'on n'a apparemment pas affaire à un maximum, de poser que le temps qu'employerait la lumière pour aller de C en E par le chemin COE, infiniment voisin de CAE, est égal, lorqu'on ne considère que les infiniment petits du premier ordre, au temps nécessaire pour parcourir le vrai chemin CAE. Dans la Fig. 53 AO ou z est la grandeur infiniment petite; comparez sur l'expression ‘infiniment petit’ la note 12 de la p. 243 du T. XVI.
Il ressort du calcul de Fermat répété par Huygens (où p désigne la résistance du premier milieu et q celle du second, ou, si l'on veut, p l'inverse de la vitesse du rayon dans le premier milieu, et q l'inverse de celle dans le second) que le rapport a : x des deux projections AB et AD, en d'autres termes celui du sinus de l'angle d'incidence à celui de l'angle de réfraction, c.à.d. l'indice de réfraction, est égal à q : p ou 1/p : 1/q, c.à.d. au quotient de la vitesse de la lumière dans le premier milieu par celle de la lumière dans le second.
-
voetnoot2)
- Lisez - 8qqppaxzz. Le signe de ce terme est d'ailleurs peu important, puisqu'il doit être négaligé comme tous les autres termes contenant z à des puissances supérieures à la première.
-
voetnoot3)
- La Pièce VII Best empruntée aux p. 78-81 du Manuscrit C. Voir les p. 267-269 de l'Avertissement qui précède.
-
voetnoot4)
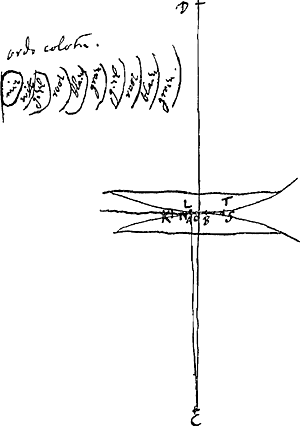
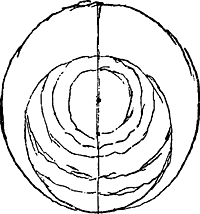
- Traduction: ordre des couleurs [a partir du centre] rien [il s'agit du cercle central de diamètre AB; voir la note 6] blanc jaune rouge bleu vert jaune rouge bleu vert. Voir aussi la note 11 de la p. 343.
-
voetnoot5)
- Donc AO ou OB [Fig. 54] = 0,07 pouce. Il s'agit évidemment d'une longueur mesurée; toutefois, comme le § 2 qui suit le fait voir, Huygens oublia de mesurer le diamètre AB dans l'expérience de la Fig. 54 et introduisit dans sa relation de l'expérience un diamètre (0,14 pouce) mesuré dans une autre expérience. Par conséquent nous ignorons le diamètre du cercle ‘sine colore’ qu'il aperçut dans l'expérience de la Fig. 54.
-
voetnoot6)
- Comme on peut le constater dans les expériences de ce genre, le cercle central est noir au milieu et devient de moins en moins foncé vers les bords sans coloration prononcée.
-
voetnoot7)
- Calcul de Huygens en centièmes de pouce, où il admet que 0,14 pouce est la vraie valeur de AB (voir la note 5) et que les lentilles, nullement déformées par la pression, se touchent en un point unique:
 En réalité la distance AL (attendu que suivant G. Quincke ‘Optische Experimental-Untersuchungen’, p. 180 du T. 129 de 1866 des ‘Annalen der Physik und Chemie’ de J.C. Poggendorff, Leipzig, A. Barth, le ‘blanc presque pur’ apparaît dans les conditions des expériences de Huygens pour une épaisseur d'air de 129 μμ, c.à.d. de 0,000129 millimètre ou 0,0000049 pouce) n'a dû être que de 0,000005 pouce environ, donc la huitième partie de la longueur calculée par Huygens. Près du centre les lentilles étaient donc fortement déformées par la pression. Il est vrai que si Huygens avait mesuré le diamètre AB (voir la note 20 de la p. 346) son calcul lui aurait fourni une valeur de AL seulement quatre fois plus grande que la vraie valeur.
En réalité la distance AL (attendu que suivant G. Quincke ‘Optische Experimental-Untersuchungen’, p. 180 du T. 129 de 1866 des ‘Annalen der Physik und Chemie’ de J.C. Poggendorff, Leipzig, A. Barth, le ‘blanc presque pur’ apparaît dans les conditions des expériences de Huygens pour une épaisseur d'air de 129 μμ, c.à.d. de 0,000129 millimètre ou 0,0000049 pouce) n'a dû être que de 0,000005 pouce environ, donc la huitième partie de la longueur calculée par Huygens. Près du centre les lentilles étaient donc fortement déformées par la pression. Il est vrai que si Huygens avait mesuré le diamètre AB (voir la note 20 de la p. 346) son calcul lui aurait fourni une valeur de AL seulement quatre fois plus grande que la vraie valeur.
-
voetnoot9)
- Calcul de Huygens:
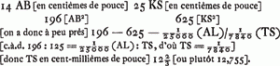 Huygens prend TS = 0,00013 pouce. Le calcul direct donne (pour KS = 0,25 et CO = DO = 120 pouces, en supposant que les lentilles, parfaitement sphériques, se touchent en un point unique) TS = 0,000143 pouce. Comme il y a lieu d'admettre une déformation des lentilles par la pression (note 7) la véritable longueur doit avoir été, pour TS comme pour AL, considérablement plus petite; comparez la note 15 qui suit.
Huygens prend TS = 0,00013 pouce. Le calcul direct donne (pour KS = 0,25 et CO = DO = 120 pouces, en supposant que les lentilles, parfaitement sphériques, se touchent en un point unique) TS = 0,000143 pouce. Comme il y a lieu d'admettre une déformation des lentilles par la pression (note 7) la véritable longueur doit avoir été, pour TS comme pour AL, considérablement plus petite; comparez la note 15 qui suit.
-
voetnoot10)
- Huygens donne le nom d'iris’ à chaque frange colorée; les couleurs énumérées dans le texte (note 4) constituent apparemment deux iris. Quoique Huygens ne le dise pas, il est certain que les différentes franges ne présentaient pas exactement la même ‘colorum varietas’; voir p.e. le tableau des couleurs dans l'article de Quincke cité dans la note 7 et reproduit par F. Kohlrausch dans son ‘Leitfaden der praktischen Physik’, p. 476 de la 8ième éd. Leipzig, Teubner, 1896.
-
voetnoot11)
- La lentille inférieure de la Fig. 54 était apparemment placée sur une table ou autre objet non transparent. La lumière du jour venait d'en haut. En disant qu'il n'y a pas de réflection ‘in circello AB’ Huygens indique que ce cercle (ou du moins la partie centrale de ce cercle: voir la note 6 de la p. 342) était noir.
-
voetnoot12)
- Longueur calculée plus haut (voir la note 7 de la p. 342). Au § 2 Huygens corrige cette fraction en 1/50000.
-
voetnoot13)
- Ceci montre clairement, comme nous le disons aussi à la fin de l'Avertissement, que Huygens considéra les couleurs qu'il aperçut comme celles d'une mince couche d'air. Il répéta plus tard (voir le No. 6 et la note 18 à la p. 183 du T. XVI) l'expérience sous le récipient de la machine pneumatique et constata que les couleurs ne disparaissent point, d'où il conclua que la mince couche d'air était encore présente. Dans la pensée de Huygens (comme dans celle de Boyle) - voir à la p. 485 du T. XIV la phrase de 1662 de Huygens ‘ex corporeis partibus aer constat sese mutuo tangentibus’ - les particules de l'air ne possèdent pas le mouvement rapide de translation qu'on leur attribue aujourd'hui.
-
voetnoot13)
- Ceci montre clairement, comme nous le disons aussi à la fin de l'Avertissement, que Huygens considéra les couleurs qu'il aperçut comme celles d'une mince couche d'air. Il répéta plus tard (voir le No. 6 et la note 18 à la p. 183 du T. XVI) l'expérience sous le récipient de la machine pneumatique et constata que les couleurs ne disparaissent point, d'où il conclua que la mince couche d'air était encore présente. Dans la pensée de Huygens (comme dans celle de Boyle) - voir à la p. 485 du T. XIV la phrase de 1662 de Huygens ‘ex corporeis partibus aer constat sese mutuo tangentibus’ - les particules de l'air ne possèdent pas le mouvement rapide de translation qu'on leur attribue aujourd'hui.
-
voetnoot14)
- Cette expression (‘la même couleur’) doit évidemment être prise ‘cum grano salis’; comparez la note 10 qui précède. On pourrait dire, pour employer l'expression de Shakespeare, que Huygens a vu ici la même couleur non seulement avec l'oeil corporel, mais aussi avec ‘the minds eye’. Voir le deuxième alinéa de la note suivante.
-
voetnoot15)
- Calcul de Huygens en cent-millièmes de pouce:
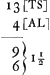 Le calcul géométrique plus correct (note 9 de la p. 342) donne pour la grandeur cherchée ⅙ (TS - AL) - toujours en admettant que AB [Fig. 54] = 0,14 pouce et que les lentilles, nullement déformées, se touchaient en un point unique - 0,000017 au lieu de 0,000015. Apparemment (notes 7 et 9 de la p. 342) ni l'un ni l'autre calcul ne mérite confiance. Huygens Le calcul géométrique plus correct (note 9 de la p. 342) donne pour la grandeur cherchée ⅙ (TS - AL) - toujours en admettant que AB [Fig. 54] = 0,14 pouce et que les lentilles, nullement déformées, se touchaient en un point unique - 0,000017 au lieu de 0,000015. Apparemment (notes 7 et 9 de la p. 342) ni l'un ni l'autre calcul ne mérite confiance. Huygens
juge à bon droit (quoique les expériences n'eussent pu confirmer nettement cette manière de voir que si elles avaient été prises avec de la lumière monochromatique et des verres non déformés) que les distances entre les deux lentilles forment une série arithmétique aux endroits correspondant à la même couleur. Partant de cette idée, il calcule en divisant par six l'épaisseur 0,000015 de la couche d'air (note 13) qui ‘ramène la même couleur’. La Fig. 55 qui se trouve à la p. 81 du Manuscrit C et doit donc, semble-t-il, avoir quelque rapport avec l'expérience des anneaux, sert peut-être à indiquer l'iddée qu'il pourrait y avoir dans les rayons de lumière une certaine périodicité (comparez la p. 268 qui précède); on pourrait même soutenir que l'idée nouvelle d'un vecteur périodique perpendiculaire à la direction du rayon a traversé l'esprit de Huygens. Si nous admettons pour un instant le nombre (considérablement trop grand) 0,000015 (une observation ultérieure donna 0,000014, voir la note 29 de la p. 347) qu'il faut multiplier par 2, vu que la lumière réfléchie traverse deux fois la couche d'air, pour trouver la longueur d'onde de la lumière monochromatique correspondante, cette lumière à longueur d'onde de 0,00003 pouce rhénan ou 0,000785 millimètre (785 μμ) serait de la lumière rouge; on trouverait 740 μμ en prenant 0,000014 au lieu de 0,000015.
Suivant le tableau de Quincke (notes 7 et 10 qui précèdent) le ‘blanc presque pur’ est suivi dans les conditions des expériences de Huygens, où la lumière incidente est celle du jour, par le jaune et ensuite par le rouge (comparez le texte de Huygens au § 1), le rouge étant à peu près pur pour une distance des lentilles de 275 μμ. La couleur rouge apparaît aussi aux endroits où la distance des lentilles est 550 μμ, 767 μμ, 1024 μμ, 1334 μμ. En moyenne l'épaisseur de la couche d'air qui ramène cette mème couleur (pour parler avec Huygens) est donc de 263 . μμ ou de 0,00001 pouce. En cent-millièmes de pouce, vu que AL = ½ (note 7 de la p. 342), le petit calcul de Huygens par lequel débute la présente note devrait donc être remplacé par 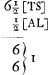 c.à.d. la distance TS [Fig. 54] doit avoir eu, semble-t-il, dans son expérience du § 1, par suite de la déformation du verre, environ la moitié de la valeur qu'il lui assigne. Nous avons vu (note 7 de la p. 342; voir aussi la note 20 qui suit) que la vraie distance AL était le quart de la distance AL selon Huygens; en effet, il paraît admissible ou même certain qu'à une plus grande distance du centre O la déformation était moindre. c.à.d. la distance TS [Fig. 54] doit avoir eu, semble-t-il, dans son expérience du § 1, par suite de la déformation du verre, environ la moitié de la valeur qu'il lui assigne. Nous avons vu (note 7 de la p. 342; voir aussi la note 20 qui suit) que la vraie distance AL était le quart de la distance AL selon Huygens; en effet, il paraît admissible ou même certain qu'à une plus grande distance du centre O la déformation était moindre.
-
voetnoot16)
- Vu que c'est là, suivant le calcul de Huygens, la distance des lentilles à l'endroit où l'on aperçoit la dernière frange.
-
voetnoot17)
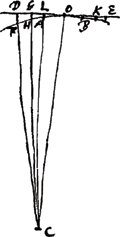
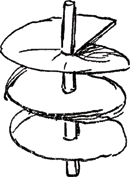
- Nous ne voyons pas que Huygens ait fait des expériences de ce genre. Exécuter une longue série d'expériences ou d'observations précises, physiques ou astronomiques, n'était d'ailleurs pas de son goût. Voir toutefois la note 13 qui précède. Au sujet de la détermination de l'épaisseur d'une mince lame de verre ou de talc que Hooke (voir l'Avertissement) n'avait pas réussi à mesurer, il ajoute: ‘Possit talis crassitudo interpositione inter lentes duas explorari, tentando quousque lamella ingrediatur angulum contactus’. L'idée de mesurer l'épaisseur d'une lame mince de cette façon (c.à.d. en cherchant jusqu'où on peut la pousser sans effort vers le point de contact de deux lentilles convexes) l'amène ensuite (p. 81-82 du Manuscrit) à mesurer d'une manière analogue la courbure des formes concaves pour tailler les lentilles. C'est à cette mesure que se rapporte la Fig. 56. Le texte qui correspond à cette figure est le suivant:
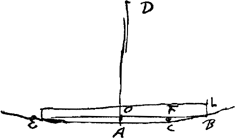 ad inveniendam diametrum formae cavae ad lentes. EL regula. FC crassitudo fili ferrei, regulam et formam hoc loco tangentis, et un peu plus loin: crassitudines 17 ∞ 22/100 poll. 22/1700 ∞ 1 crassitudo FC. BE ∞ 736. BO ∞ 368. BF ∞ 250. Le calcul ex filo interposito inter modulum et regulam ou inter lentem et regulam lui donne ensuite 45 pieds pour le rayon de courbure de la forme ou de la lentille et il ajoute: Ex reflexione deinde inveni radium hunc eundem 45 pedum.
ad inveniendam diametrum formae cavae ad lentes. EL regula. FC crassitudo fili ferrei, regulam et formam hoc loco tangentis, et un peu plus loin: crassitudines 17 ∞ 22/100 poll. 22/1700 ∞ 1 crassitudo FC. BE ∞ 736. BO ∞ 368. BF ∞ 250. Le calcul ex filo interposito inter modulum et regulam ou inter lentem et regulam lui donne ensuite 45 pieds pour le rayon de courbure de la forme ou de la lentille et il ajoute: Ex reflexione deinde inveni radium hunc eundem 45 pedum.
-
voetnoot19)
- C.à.d. noir: comparez les notes 4 et 6 de la p. 342.
-
voetnoot20)
- Calcul de Huygens en centièmes de pouce:
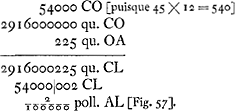 Comparez la note 7 de la p. 342, suivant laquelle la distance AL de la Fig. 57 - moitié de la distance AL (calculée en partant d'une fausse valeur du diamètre AB) du § 1 [Fig. 54] - doit en réalité avoir été environ quatre fois plus petite. Comparez aussi la note suivante.
Comparez la note 7 de la p. 342, suivant laquelle la distance AL de la Fig. 57 - moitié de la distance AL (calculée en partant d'une fausse valeur du diamètre AB) du § 1 [Fig. 54] - doit en réalité avoir été environ quatre fois plus petite. Comparez aussi la note suivante.
-
voetnoot21)
- En d'autres termes: en écrivant le § 1 Huygens a commis, dit-il, une erreur en donnant au diamètre AB [Fig. 54] la valeur de 0,14 pouce, valeur qui avait été mesurée dans une autre expérience non relatée où l'une des deux surfaces était plane, l'autre convexe avec un rayon de courbure de 10 pieds (120 pouces). Il aurait pu ajouter (puisqu'il suppose les lentilles non déformées et se touchant en un seul point) qu'on obtient la valeur AL = 1/50000 pouce dans le cas de la Fig. 54, comme dans celui de la Fig. 57, en admettant que dans le cas de la Fig. 54 le diamètre AB non mesuré avait une longueur de 0,10 pouce. La suite du texte (‘KS recte se habet etc.’) fait voir que les expériences de la ‘pagina praecedens’, c.à.d. du § 1, furent réellement exécutées avec deux lentilles convexes comme l'indique la Fig. 54.
-
voetnoot25)
- Ceci s'accorde avec le § 1: Huygens y avait également trouvé 0,00013 pouce pour l'épaisseur correspondante TS de la Fig. 54, c.à.d. pour la plus grande épaisseur de la couche d'air montrant des couleurs. Comme nous l'avons dit dans les notes 9 de la p. 342 et 15 de la p. 343 la vraie valeur doit avoir été plus petite dans l'une et l'autre expérience. Nous en concluons que dans la deuxième expérience, comme dans la première, les surfaces ont été fortement serrées l'une contre l'autre et par conséquent déformées.
-
voetnoot27)
- C.à.d. suivant l'interprétation de Huygens les couleurs apparaissent pour la première fois, dans une couche d'air d'épaisseur croissante, lorsque cette épaisseur est devenue égale à 0,000033 pouce. Vu la déformation du verre (note 25) la vraie valeur doit être plus petite. Huygens ne fait aucune mention de la largeur des franges. Si nous admettons pour fixer les idées, comme nous l'avons fait dans le dernier alinéa de la note 15 de la p. 343, que la frange colorée apparaît selon lui au moment où la couleur rouge se montre, il faut et conclure (vu que le tableau de Quincke donne 268 à 275 μμ pour l'épaisseur de la couche d'air à cet instant, et que 278 μμ = 0,000011 pouce) que la vraie longueur GH était environ le tiers de la longueur GH selon Huygens. Ce rapport 1 : 3 s'accorde fort bien avec les rapports 1 : 4 (distance AL) et 1 : 2 (distance TS) adoptés plus haut (fin de la note 15 de la p. 343).
-
voetnoot28)
- Entre les points D et G [Fig. 57] Huygens apercevait donc 6 franges colorées, de sorte qu'il en voyait 8 en tout.
-
voetnoot29)
- Ici aussi - comparez les notes 14 et 15 qui précèdent - Huygens, voyant évidemment que les franges se resserrent à mesure qu'elles s'éloignent du centre, admet à bon droit qu'il faut une couche d'air d'une épaisseur déterminée pour ramener la même couleur. Il trouve ici pour cette épaisseur 1/70000 ou 0,000014 pouce, ce qui s'accorde avec la valeur 0,000015, trouvée précédemment en attribuant faussement au diamètre AB (Fig.54) une longueur de 0,14 pouce. Comme nous l'avons dit dans la note 15 de la p. 343, la valeur que Huygens aurait trouvée s'il avait pu tenir compte correctement de la déformation du verre aurait été plus petite.
-
voetnoot30)
- Suivant Huygens - mais nous avons vu que ses mesures (notamment le nombre 0,000034) ne méritent pas confiance - une couche d'air horizontale, éclairée d'en haut et se trouvant au-dessus d'un objet non transparent (voir la note 11 de la p. 343) montre donc des couleurs à un observateur qui regarde d'en haut lorsque son épaisseur est située entre les limites 0,000034 et 0,000134 pouce (0,00089 et 0,0035 millimètre). Des franges colorées (du moins colorées lorsqu'on les examine au microscope) y apparaissent aux endroits où l'épaisseur est E = 0,000034 + 0,000014
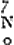 pouce ou 890 + 370 pouce ou 890 + 370 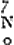 μμ (millionième de millimètre). La véritable formule aurait plutôt été E = 0,000011 + 0,000010 μμ (millionième de millimètre). La véritable formule aurait plutôt été E = 0,000011 + 0,000010
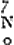 pouce ou 275 + 263 pouce ou 275 + 263  μμ. μμ.
-
voetnoot1)
- La Fig. 58, empruntée à la p. 80 du Manuscrit C (comparez la note 3 de la p. 342) représente apparemment les franges telles qu'on les aperçoit en regardant les verres des Fig. 54 ou 57 obliquement. On trouve à la même page encore quelques autres figures de ce genre.
|