|
-
voetnoot1)
- Cette section a été empruntée à une feuille séparée, pliée deux fois de manière à laisser à découvert quatre pages dont deux contiennent chacune une des figures que nous reproduisons avec les annotations qui les accompagnent.
-
voetnoot2)
- Il s'agit du troisième passage de Mercure qui ait jamais été observé, le premier étant celui de 1631, observé par Gassendi, et le second celui de 1651, observé à Surat (près de Bombay) par Shakerley. Huygens jugea le phénomène d'une telle importance qu'il y sacrifia la fête du couronnement du Roi (voir à la p. 70 l'annotation du 3 mai 1660). Huygens a donné un court exposé de son observation dans une lettre à Boulliau (p. 279-281 du T. III) où toutefois, dans la figure de la p. 281, Huygens écrivit par mégarde ‘Ecliptica’ où l'on doit lire ‘Semita Mercurij’ (voir la p. 314 du T. III); il y revint dans une lettre à Hevelius (p. 314 du T. III). On trouve encore d'autres renseignements aux pp. 268, 290, 293, 309 et 438 du même Tome. Il en résulte que le président de la Société Royale de Londres, Robert Moray, pria Huygens de vouloir ‘faire quelque memoire pour ceux qui obserueront la coniunction du ☉ & de ☿ des choses qu'ils ont a remarquer.’ Le jour de l'évènement Huygens se rendit au logis, dans le Longacre, du ‘bon faiseur de lunettes’ John Reeves (le ‘Reefs τελεσϰοπιοποιός’ de la Fig. 38), où il ne trouva pas toute la commodité qu'il aurait souhaitée (p. 280 et 314). D'ailleurs des nuées ne permettaient d'observer le soleil que pendant une demi-heure (p. 280). Quelques observateurs anglais qui s'étaient installés dans un autre endroit de Londres avaient été encore moins heureux. Après avoir attendu tout le matin, ils s'étaient éloignés
pour prendre un repas lorsque l'observation devint possible.
Voir encore pour l'explication de la figure 38 la note suivante.
-
voetnoot3)
- Afin de discuter cette figure, désignons par S le centre du soleil et par EE′ l'écliptique passant par ce centre (E du côté droit, c'est-à-dire Est) et faisant un angle de 45o14′ avec la verticale (le diamètre tracé par les deux gros points). Cet angle se calcule aisément comme la différence entre l'angle que fait l'écliptique avec le cercle de déclinaison passant par le soleil (pour le 3 mai) et l'angle parallactique du Soleil (pour 2 heures). Comme AB = 260″ et
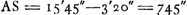 , l'angle BSA s'évalue à 20o26′. D'où. , l'angle BSA s'évalue à 20o26′. D'où. 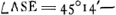 , et les coördonnées écliptiques de Mercure par rapport au soleil dans l'observation de deux heures: λ = + 11′16″, β = + 5′12″. , et les coördonnées écliptiques de Mercure par rapport au soleil dans l'observation de deux heures: λ = + 11′16″, β = + 5′12″.
-
voetnoot4)
- Nous ne savons pas expliquer complètement les petits calculs qu'on trouve sur les pages qui contiennent les figures 38 et 39. Toutefois il nous semble qu'ils doivent se rapporter à la détermination de la durée totale du passage. En effet, les nombres 58 et 41 qu'on trouve à lap. 21 a désignent probablement les mouvements diurnes en longitude du soleil et de Mercureau 3 mai 1661. Ce dernier mouvement étant rétrograde on trouve 99′ pour le mouvement en longitude de Mercure par rapport au Soleil. De même 17 peut désigner le mouvement diurne de Mercure en latitude. On a donc
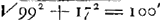 pour le mouvement diurne total par rapport au Soleil. Posant 31′ pour la corde parcourue sur le Soleil, il résulte une durée de 7½ heures pour le passage, durée qui fut estimée par Hevelius à 8 heures (voir la p. 290 du T. III). pour le mouvement diurne total par rapport au Soleil. Posant 31′ pour la corde parcourue sur le Soleil, il résulte une durée de 7½ heures pour le passage, durée qui fut estimée par Hevelius à 8 heures (voir la p. 290 du T. III).
88 est peut-être la valeur, adoptée primitivement pour le déplacement diurne en longitude de Mercure sur le Soleil, qui fut remplacée ensuite per 99.
-
voetnoot7)
- ♉ 13o27′, ou 43o27′, est la longitude du Soleil à l'époque de l'observation.
-
voetnoot8)
- Cette valeur est obtenue par la proportion suivante qu'on trouve sur une autre page du même manuscrit: 1296000″ [ad] 1440′ [ut] 3548⅓ [ad] 3.56. Ici 1296000″ = 360o,
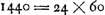 , tandis que 3548⅓ signifie le déplacement diurne en secondes du soleil par rapport aux étoiles, supputé par Huygens par l'opération , tandis que 3548⅓ signifie le déplacement diurne en secondes du soleil par rapport aux étoiles, supputé par Huygens par l'opération 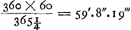 (ou plutôt 59′.8″.15‴, puisqu'il y une légère erreur dans le calcul). Or, il est aisé de voir que la valeur 3.56, calculée de cette manière un peu compliquée, désigne la différence en minutes et secondes entre le jour sidéral et le jour moyen solaire. (ou plutôt 59′.8″.15‴, puisqu'il y une légère erreur dans le calcul). Or, il est aisé de voir que la valeur 3.56, calculée de cette manière un peu compliquée, désigne la différence en minutes et secondes entre le jour sidéral et le jour moyen solaire.
|