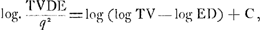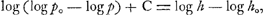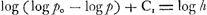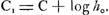Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 431]
| ||||||||||||
Avertissement.Recherches de 1661 et 1662 sur le calcul des logarithmes et sur la quadrature de l'hyperbole par les logarithmes. Application à la détermination de l'altitude qui correspond à une hauteur donnée de la colonne barométrique et réciproquement.
En 1868, Joseph Bertrand découvritGa naar voetnoot1) dans le ‘Registre des procès verbaux de l'Académie des Sciences’ une ‘règle pour trouver les logarithmes’, communiquée par Huygens à cette Assemblée, en 1666, dans l'une de ses premières réunions. Bertrand jugea cette règle ‘remarquable et élégante en elle-même et la démonstration que Huyghens ne donne pas’ lui parut ‘difficile à faire sans recourir à la série logarithmique de MercatorGa naar voetnoot2), publiée seulement en 1668Ga naar voetnoot3) et présentée à cette date par Huyghens lui-même dans l'une des séances de l'AcadémieGa naar voetnoot4)’. | ||||||||||||
[pagina 432]
| ||||||||||||
Or, la Pièce No. I (p. 451-457), datée d'août 1661, nous donne la solution de cette énigme. Elle nous fait connaître la méthode suivie par Huygens pour trouver sa règle; méthode qui, en effet, n'a rien à faire avec la série de Mercator, puisqu'elle s'appuie sur une quadrature approchée de l'hyperbole, déduite par Huygens d'un théorème qu'il avait publié en 1651 dans ses ‘Theoremata de quadratura hyperboles, ellipsis et circuli ex dato portionum gravitatis centro’.
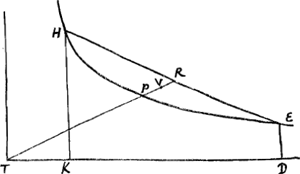 Suivant ce théorèmeGa naar voetnoot1) on peut calculer l'aire d'unsegment hyperbolique HPERHGa naar voetnoot2) pourvu qu'on connaisse la situation du centre de gravité V sur le diamètre PR. Si donc, on remplace, par première approximation, le segment hyperbolique par un segment parabolique construit sur le même diamètre PR et sur la même base HE, il est facile de trouver une valeur approchée pour l'aire du segment HPE (et, par suite, aussi pour celle de la figure mixtiligne HKDEPHGa naar voetnoot3)), puisqu'on sait que dans un segment parabolique le centre de gravité divise le diamètre PR dans la raison de 3 à 2. Considérons maintenant la figure suivante, qui correspond à celle de la p. 451 du texte qui suit. Par un théorème dû à Grégoire de St. VincentGa naar voetnoot4) Huygens savait que les aires des figures mixtilignes ABDEA et FGDEF sont | ||||||||||||
[pagina 433]
| ||||||||||||
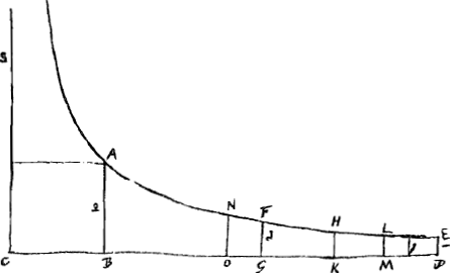 proportionnelles aux logarithmes des rapports des ordonnées extrêmes. Posant donc DE = 1, AB = 10, FG = β, on a: 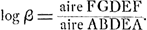
Si Huygens avait appliqué directement sa quadrature approximative aux aires FGDEF et ABDEA, le résultat aurait été très peu satisfaisantGa naar voetnoot5), mais l'approximation devient évidemment meilleure à mesure qu'on rapproche les ordonnées extrêmes AB et FG de DE sans changer le rapport des aires. Afin de profiter de cette circonstance, Huygens divise l'aire ABDE en deux parties égales par l'ordonnée NO, moyenne proportionnelle entre AB et DE, et il agit de la même façon avec l'aire FGDE. Répétant cinq fois ces opérations, il obtient des figures, limitées à droite par l'ordonnée DE, dont les aires sont la trentedeuxième partie respectivement des aires ABDE et FGDE. Or, c'est à celles-ci qu'il applique sa méthode. Pour vérifier ensuite l'efficacité de sa règle, il l'emploie au calcul de log 2, avec le résultat qu'il trouve ‘10 characteres vrais et l'unzième qui surpasse le vray de l'unitè’Ga naar voetnoot6). Entièrement satisfait de ce résultat, il annonce sa découverte le 1 août 1661 à Moray dans les termes suivantsGa naar voetnoot7): ‘Je me suis occupè pendant quelques jours a estudier la musique, et la diuision du monochorde à la quelle j'ay appliquè heureusement l'algebreGa naar voetnoot8). J'ay aussi trouuè que les logarithmes y sont de grand usage, et de la je me suis mis a considerer ces merveilleux nombres et admirer | ||||||||||||
[pagina 434]
| ||||||||||||
l'industrie et la patience de ceux qui nous les ont donnez. Que si la peine n'en estait desia prise, j'ay une regle pour les trouuer avec beaucoup de facilitè, et non pas la vingtieme partie du travail qu'ils ont coustè’. Comme nous l'avons vu, Huygens communiqua sa règle en 1666 à l'Académie des Sciences. En novembre 1667 il la mentionne dans une lettre au Prince Léopoldo de MedicisGa naar voetnoot1) parmi les travaux qu'il tient en réserve parce qu'il n'y a pas encore mis la dernière main. Enfin, dans le Journal des scavans du 2 juillet 1668Ga naar voetnoot2), il fait allusion à sa Règle en faisant remarquer, à propos de ce qui est dit sur le rapport entre les logarithmes et la dimension de l'hyperbole dans un livre de Gregory ‘que Messieurs de l'Assemblée ne le trouveroient pas nouveau, puisqu'ils pourroient se souvenir qu'il leur a desja proposé la même chose, & que la regle qu'il a donnée pour trouver les Logarithmes est insérée il y a longtemps dans leur Registre’. Onze mois après la découverte de sa règle, Huygens aperçut que la quadrature approchée de l'hyperbole, qu'il y avait appliquée, était encore susceptible d'une autre application non moins importante. Il s'agit de la quadrature de 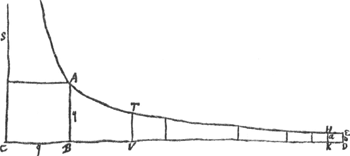 l'hyperbole par les logarithmesGa naar voetnoot3). Du théorème de Grégoire de St. Vincent, que nous avons cité plus hautGa naar voetnoot4), il fuit que le rapport de l'espace hyperbolique TVDEGa naar voetnoot5) au carré caractéristique AC est proportionnel à la différence des logarithmes de TV et de ED. On a donc: | ||||||||||||
[pagina 435]
| ||||||||||||
où q représente le côté AB du carré caractéristique, et où C est une constante. Afin d'obtenir une formule commode pour calculer l'aire d'un espace hyperbolique comme TVDE, il suffit donc de déterminer, une fois pour toutes, la valeur de la constante C. À cet effet Huygens applique sa quadrature approchée à l'espace HKDE où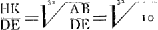 . Profitant des calculs qu'il avait déjà accomplis en 1661, il trouve pour cet espace 719557838,5Ga naar voetnoot6), savoir, en supposant DE = 104 et AB = q = 105. Il s'en suit: . Profitant des calculs qu'il avait déjà accomplis en 1661, il trouve pour cet espace 719557838,5Ga naar voetnoot6), savoir, en supposant DE = 104 et AB = q = 105. Il s'en suit:
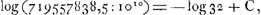
ce qui permet de calculer la valeur de C, pour laquelle Huygens, se servant des tables de Vlacq à dix mantissesGa naar voetnoot7), trouve 0,3622156868; nombre qu'il a remplacé plus tard par 0,3622156887Ga naar voetnoot8) à la suite d'un nouveau calcul que nous ne connaissons pas. Or, on sait par l'analyse moderne qu'on a: 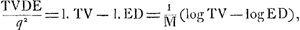
où M est le module du système ordinaire des logarithmes. Il en résulte C = - log M = - log log e = 0,362215688699..., ce qui prouve l'exactitude des calculs de Huygens et surtout du dernier calcul dont les détails nous sont inconnus. Ayant trouvé ainsi la règle pour la quadrature de l'hyperbole par les logarithmes, il l'applique d'abord à quelques exemples numériquesGa naar voetnoot9) et il montre ensuite comment elle peut servir au calcul de l'aire d'un segment hyperbolique quelconqueGa naar voetnoot10) et à la rectification de la paraboleGa naar voetnoot11), qu'il avait apprise à réduire, cinq ans plus tôtGa naar voetnoot12), à la quadrature de l'hyperbole. | ||||||||||||
[pagina 436]
| ||||||||||||
Puis, le lendemain de la rédaction de la Pièce No. III que nous venons d'analyser, une application bien autrement intéressante se présenta à luiGa naar voetnoot1). Quelques mois auparavant, en mars 1662Ga naar voetnoot2), Moray l'avait averti de la relation simple, récemment découverte par Boyle, d'après laquelle le volume d'une quantité donnée d'air est inversement proportionnel à la pression à laquelle on la soumet. À la description succincte de l'une des expériences de Boyle, Moray avait ajouté la phrase un peu énigmatique: ‘Je crois que vous comprendrez assez bien par cette courte description que cecy en veut à l'Atmosphere, mais comme que cen soit J'ay trop de besogne de reste, pour m'y arrester plus long temps’. En réponseGa naar voetnoot3), Huygens demanda des renseignements sur un point important qui lui était resté douteux; du reste il ne voyait pas encore qu'il fût fort aisé de déduire des expériences de Boyle la hauteur de l'atmosphère, il croyait que pour cela on aurait besoin encore d'autres expériences, comme celles qu'on avait fait en France sur les montagnes d'AuvergneGa naar voetnoot4). Cependant, avant d'avoir obtenu l'éclaircissement demandéGa naar voetnoot5), Huygens reçut le 12 juillet l'ouvrage de BoyleGa naar voetnoot6) où celui-ci donne en détail les résultats de deux séries d'expériences touchant la condensation et la raréfaction de l'air. Ayant pris connaissance de ces résultats ‘qui prouvent’ comme il s'exprimeGa naar voetnoot7) ‘assez clairement cette proprietè remarquable [de l'air] a sçavoir que la force de son ressort suit la proportion contraire des espaces ou il est reduit’, Huygens ne doutait plus de l'exactitude approximativeGa naar voetnoot8) de la loi de Boyle. Quelques jours aprèsGa naar voetnoot9), il se mit à l'oeuvre pour chercher la relation qui devait exister entre l'altitude au-dessus de la mer | ||||||||||||
[pagina 437]
| ||||||||||||
et la hauteur de la colonne barométrique, dans l'hypothèse que la diminution de la pression dans les couches diverses de l'atmosphère se conforme entièrement à la loi récemment découverteGa naar voetnoot10). En effet, par un raisonnement subtil, pour lequel nous renvoyons au texte de la Pièce No. IVGa naar voetnoot11), Huygens trouve une relation qui est équivalente à la formule, en notation moderne:  où ho désigne la hauteur fictive jusqu'à laquelle l'atmosphère s'étendrait si sa densité était partout égale à celle de la couche d'air qui se trouve au niveau de la mer, où h indique l'altitude du lieu, v le volume d'une particule d'air à cette altitude, p la pression à laquelle elle y est soumise, et ensin vo le volume de cette même particule transportée au niveau de la mer où la pression est po. Or, puisque, d'après la loi de Boyle, on a v = vopo/p, il est évident que la détermination de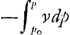 se réduit à la quadrature d'un espace hyperbolique auquel la formule (1), p. 435, est applicable lorsqu'on y remplace q2 par povo. De cette façon on trouve: se réduit à la quadrature d'un espace hyperbolique auquel la formule (1), p. 435, est applicable lorsqu'on y remplace q2 par povo. De cette façon on trouve:
où C représente la constante de Huygens que nous avons trouvée égale à - log log e. C'est là, à part une petite complication sur laquelle nous n'insistons pas iciGa naar voetnoot12), la formule qui correspond au calcul de la p. 486 du texte; mais puisque ho est une constante (du moins lorsque l'unité de longueur qu'on emploie à mesurer les altitudes est donnée) on peut écrire:
| ||||||||||||
[pagina 438]
| ||||||||||||
Pour supputer la valeur de ho, Huygens devait connaître la hauteur de la colonne barométrique au niveau de la mer, qu'il suppose égale à 30 pouces anglaisGa naar voetnoot1), et le rapport du poids spécifique du mercure à celui de l'airGa naar voetnoot2). Il trouve de cette façon 32640 pieds anglais pour la hauteur fictive ho de l'atmosphère supposée homogène, nombre qu'il remplace par le nombre rond 33000. À l'aide de cette donnée on trouve C1 = 4,88073; mais, par suite de la complication mentionnée, les calculs abrégés, que Huygens fait suivreGa naar voetnoot3), sont mieux représentés par la formule:
où 0,11927 est le ‘numerus perpetuus’ qui entre dans tous les calculs. Ayant appliqué la règle qu'il venait d'obtenir à plusieurs exemplesGa naar voetnoot3), il communique, le 17 août 1662, à son frère Lodewijk les résultats de deux d'entre euxGa naar voetnoot4), le priant d'en faire part au duc de RoanezGa naar voetnoot5), un de ses amis parisiens. Le lendemain il exposa sa règle, appliquée à trois exemples, à MorayGa naar voetnoot6), sans toutefois en faire connaître la démonstration.
Si dans la Pièce No. IV, dont nous nous sommes occupés jusqu'ici, Huygens discute des exemples fictifs, dans l'Appendice I (p. 491-494), de date inconnue, que nous avons ajouté à cette Pièce, il discute les célèbres expériences faites par Perier au Puy de Dôme en Auvergne sur l'instigation de Pascal. À cet effet il devait commencer par changer le ‘numerus perpetuus’ pour l'adapter à l'emploi du pied de Paris, qui remplace le pied anglais des calculs précédentsGa naar voetnoot7); ensuite il applique sa règle aux données fournies par Perier, pour en | ||||||||||||
[pagina 439]
| ||||||||||||
déduire entre autres l'altitude du sommet du Puy de Dôme. Il trouve pour cette altitude une valeur qui, même après la correction notable que nous y avons apportéeGa naar voetnoot8), est trop forte; conséquence nécessaire de l'hypothèse dont il partGa naar voetnoot9). Enfin, beaucoup plus tard, en 1673, Huygens s'est occupé encore une dernière fois du même sujet à propos d'une expérience de Cassini faite sur une montagne près de ToulonGa naar voetnoot10). | ||||||||||||
La courbe logarithmique.Il y a lieu de s'étonner que les recherches sur la courbe logarithmique qu'on trouve dans la Pièce No. II (p. 460-471) (quoiqu'elle n'y soit pas encore indiquée sous ce nom) portent une date si ancienne que celle de septembre 1661. En effet Huygens ne mentionne ces recherches, ni dans sa lettre à Leopoldo de MedicisGa naar voetnoot11), du 19 novembre 1667, où il énumère ses travaux encore inédits, ni dans le reste de sa correspondance antérieure à sa lettre à Leibniz du 23 février 1692Ga naar voetnoot12), ni dans l'‘Horologium oscillatorium’ de 1673, où il donne tant de résumés de ses travaux mathématiques pas encore publiésGa naar voetnoot13). Cependant la date en question est inscrite en tête de la Pièce No. II, d'une manière tout-à-fait distincte, ne permettant aucun doute. Il s'en suit que, lorsque les résultats concernant une ligne courbe qu'il avait ‘examinée longtemps auparavant’ et qu'il proposa d'appeler ‘Logarithmique’ ou ‘Logistique’, furent publiés enfin, sans leurs déductions, dans son ‘Discours de la cause de la pesanteur’Ga naar voetnoot14), ils avaient été connus à Huygens pour la grande majorité, et quant aux plus importants, depuis presque trente ans. Les déductions qui manquent dans ce ‘Discours’, on les trouve, pour la plupart, dans la Pièce No. II. Commençons par observer que chez la ‘Logarith- | ||||||||||||
[pagina 440]
| ||||||||||||
mique’ les abscisses, comme ADGa naar voetnoot1), sont proportionnelles aux logarithmes des ordonnées HD, pourvu qu'on prenne AK pour unité de longueur des ordonnées. Cette courbe peut donc servir à exécuter graphiquement toutes les opérations auxquelles on emploie les logarithmesGa naar voetnoot2). Or, ce qu'il y a de remarquable, c'est
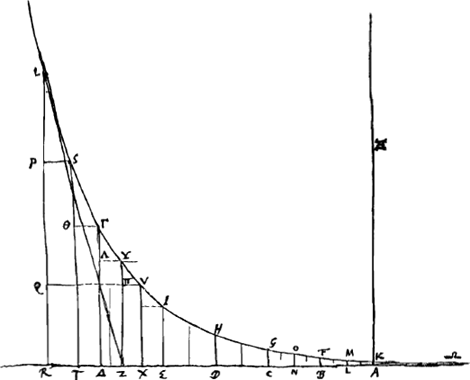 qu'on peut construire la logarithmique par points sans recourir à une table de logarithmes. Huygens, à cet effet, porte sur l'axe des x successivement les segments égaux AB, BC, CD, etc. et il prend chaque fois l'ordonnée, qui correspond à l'extrémité d'un tel segment, égale au double de celle du point de division qui précède; de sorte qu'on a BF = 2AK, GC = 4AK, HD = 8AK, etc. Ensuite, afin d'interpoler d'autres points entre les points K, F, G, H, etc., il | ||||||||||||
[pagina 441]
| ||||||||||||
suffit de diviser chaque segment en deux parties égales par les points L, N, etc., d'y ériger des ordonnées qui sont les moyennes proportionnelles entre celles des points extrêmes du segment, et de répéter cette opération sur les nouveaux segments, toujours plus petits, autant de fois qu'on le désireGa naar voetnoot3). C'est de cette construction que Huygens se sert pour formuler la définition de la courbeGa naar voetnoot4). Il en conclut d'abord que les abscisses peuvent être considérées comme les logarithmes des ordonnées et que deux ordonnées dont la distance de l'une à l'autre est donnée sont partout dans le même rapportGa naar voetnoot5). Partant de cette dernière propriété, il sait en déduire, par voie géométrique, plusieurs autres, parmi lesquelles nous signalons l'invariabilité de la longueur de la soustangenteGa naar voetnoot6) dont le rapport à la distance entre deux ordonnées dont l'une est le double de l'autre, est trouvé égal à celui de 0,434294481903251804Ga naar voetnoot7) à log 2. Il trouve par la même voie la quadrature de l'espace compris entre deux ordonnéesGa naar voetnoot8), la situation du centre de gravité de l'espace qui s'étend à l'infini entre la courbe et l'asymptote depuis une ordonnée donnéeGa naar voetnoot9), puis les cubatures des solides engendrés par la révolution d'un tel espace respectivement autour de l'asymptoteGa naar voetnoot10) et autour de l'or- | ||||||||||||
[pagina 442]
| ||||||||||||
donnéeGa naar voetnoot1). Enfin Huygens ajoute, sans démonstration, deux théorèmes qui font connaître la situation du centre de gravité dans l'un et dans l'autre de ces solidesGa naar voetnoot2). Assurément la Pièce que nous venons d'analyser est un des plus beaux exemples de ce que les meilleurs géomètres du dix-septième siècle savaient accomplir avant l'invention de l'algorithme du calcul différentiel et intégral. | ||||||||||||
Détermination de la tangente à une courbe algébrique.La règle pour déterminer les tangentes d'une courbe algébrique quelconque donnée par son équation cartésienne fμ (x, y) = 0, telle qu'elle fut exposée par Huygens dans le manuscrit qui accompagna sa lettre à Johan de Witt du 25 février 1663Ga naar voetnoot3), semble être une extension si naturelle de la méthode de Fermat, surtout après la simplification que Huygens y avait apportéeGa naar voetnoot4), qu'on croirait que Huygens a dû la découvrir aussitôt qu'il se fut posé le problème en question. Cependant les manuscrits nous montrent qu'il en a été tout autrement. Dans le fait, Huygens, avant d'arriver à la solution que nous connaissons, en avait trouvé d'autres assez intéressantes, mais beaucoup plus compliquées. L'impulsion à de nouvelles recherches sur les tangentes lui fut donnée par une lettre de de Sluse datée du 18 août 1662Ga naar voetnoot5). Dans cette lettre celui-çi annonça qu'il avait perfectionné une méthode, inventée il y avait plusieurs années, de telle façon qu'il pouvait trouver les tangentes d'une courbe, presque sans calcul, par la seule inspection des termes de son équationGa naar voetnoot6). Comme un exemple des | ||||||||||||
[pagina 443]
| ||||||||||||
résultats auxquels cette méthode pouvait conduire, il décrivit la construction de la tangente à une certaine courbe qui lui fut proposée jadis par van GutschovenGa naar voetnoot7). L'équation de cette courbe peut s'écrire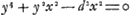 . Elle est facilement résoluble par rapport à x2, de sorte qu'on a . Elle est facilement résoluble par rapport à x2, de sorte qu'on a 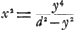 . Or, quoique Huygens ne pût pas croire que la méthode de de Sluse fût basée sur cette particularitéGa naar voetnoot8), il commença toutefois par chercher les moyens de déterminer les tangentes d'une courbe x2 = f(y), au cas où f(y) représente une fonction rationnelle, entière ou fractionnaireGa naar voetnoot9). . Or, quoique Huygens ne pût pas croire que la méthode de de Sluse fût basée sur cette particularitéGa naar voetnoot8), il commença toutefois par chercher les moyens de déterminer les tangentes d'une courbe x2 = f(y), au cas où f(y) représente une fonction rationnelle, entière ou fractionnaireGa naar voetnoot9).
Pour des raisons qu'il est difficile de deviner, Huygens n'appliqua pas à ce problème la méthode de Fermat telle qu'il l'avait simplifiée, mais il chercha d'autres méthodes par lesquelles le problème est réduit à celui de trouver le maximum ou minimum d'une fraction algébrique φ(y)/ψ(y); problème qui avait été résolu par HuddeGa naar voetnoot10). La première de ces méthodes rappelle fortement celle inventée par Descartes pour déterminer les tangentes, ou plutôt les normales, d'une courbe donnéeGa naar voetnoot11). 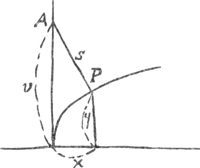 Soit, afin d'exposer cette méthode, s la ligne qui joint le point A de l'axe des y à un point P de la courbe, de sorte qu'on a: 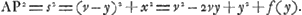
Si, ensuite, nous déplaçons le point P le long de la courbe, cette expression pour s2 sera stationnaire (c'est-à-dire elle sera en général maxi- | ||||||||||||
[pagina 444]
| ||||||||||||
mum on minimum) à l'instant où la ligne s devient normale à la courbe. L'application de la méthode de Hudde amène donc dans ce cas une équation, qui, en notation moderne, s'écrit: 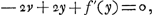 et dont on déduit
et dont on déduit 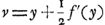 ; ce qui permet de construire la normale AP et, par suite, aussi la tangente du point PGa naar voetnoot1).
La deuxième méthode est plus originale. Cette fois Huygens choisit le point fixe A sur la tangente elle-même, savoir à son point d'intersection avec l'axe des ; ce qui permet de construire la normale AP et, par suite, aussi la tangente du point PGa naar voetnoot1).
La deuxième méthode est plus originale. Cette fois Huygens choisit le point fixe A sur la tangente elle-même, savoir à son point d'intersection avec l'axe des
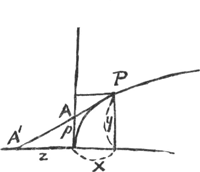 y. C'est alors l'expression 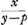 , ou si l'on veut , ou si l'on veut 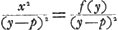 , qui doit devenir un maximum ou minimum au cas où la ligne AP, qui joint le point fixe A au point mobile P de la courbe, est tangente en P à cette courbe. Par cette condition on trouve , qui doit devenir un maximum ou minimum au cas où la ligne AP, qui joint le point fixe A au point mobile P de la courbe, est tangente en P à cette courbe. Par cette condition on trouve 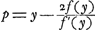 Ga naar voetnoot2).
Évidemment on peut varier cette dernière méthode en fixant un autre point de la tangente, p.e. le point d'intersection A′ avec l'axe des x. Dans ce dernier cas il s'agit de rendre un maximum ou un minimum la fraction Ga naar voetnoot2).
Évidemment on peut varier cette dernière méthode en fixant un autre point de la tangente, p.e. le point d'intersection A′ avec l'axe des x. Dans ce dernier cas il s'agit de rendre un maximum ou un minimum la fraction 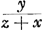 . Huygens applique cette méthode à des cas où y2 = f (x)Ga naar voetnoot3). On trouve alors, par la condition du maximum ou minimum de . Huygens applique cette méthode à des cas où y2 = f (x)Ga naar voetnoot3). On trouve alors, par la condition du maximum ou minimum de 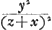 , l'équation , l'équation 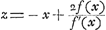 . .
| ||||||||||||
[pagina 445]
| ||||||||||||
Ces méthodes n'exigent que des calculs très simples dans les cas où Huygens les emploie; mais elles ne sont pas applicables lorsque la courbe est donnée par une équation algébrique quelconque fμ(x, y) = 0, irrésoluble par rapport à x et à y. Pour ce cas Huygens imagina deux autres méthodesGa naar voetnoot4) dont toutefois il n'était nullement satisfait. En effet, le 25 septembre 1662, il manda à de SluseGa naar voetnoot5): ‘J'aurais déjà répondu plus tôt à votre avant-dernièreGa naar voetnoot6), n'était-ce que je me proposais d'examiner quelques choses concernant votre nouvelle invention, à quoi j'ai eu à peine le loisir, il y a seulement quelques jours. Car j'ai été surpris de ce que vous écrivez de la concision de la méthode trouvée par vous pour les tangentes des courbes; j'ai travaillé beaucoup pour découvrir en quoi elle pouvait consister, mais en vain. Il est vrai que j'ai trouvé sans difficulté la tangente, que vous proposez, de la courbe de Gutschoven, et cela de plusieurs manièresGa naar voetnoot7) et par un calcul très bref qui occupe à peine deux de ces lignes-ci. Et je suis tombé aussi sur votre constructionGa naar voetnoot8); mais pourtant il me semble, d'après vos paroles, que vous avez inventé une règle de plus grande portée, s'étendant à toutes les courbes dont la nature est exprimée par une | ||||||||||||
[pagina 446]
| ||||||||||||
équation; savoir aussi à celles dont l'équation est en quelque façon implicite, comme 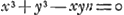 , ce qui est l'équation de la courbe que vous avez peut-être rencontrée dans les commentaires de van Schooten sur DescartesGa naar voetnoot1)... Je n'ai trouvé la tangente à cette courbe que par un calcul médiocrement prolixeGa naar voetnoot2) (savoir en me servant de cette équation-là, car la chose peut être accomplie beaucoup plus commodément par une autre voieGa naar voetnoot3)) et j'admirerai beaucoup votre methode si elle enseigne à trouver cette tangente presque sans aucun calcul et par la seule inspection des termes de l'équation’. , ce qui est l'équation de la courbe que vous avez peut-être rencontrée dans les commentaires de van Schooten sur DescartesGa naar voetnoot1)... Je n'ai trouvé la tangente à cette courbe que par un calcul médiocrement prolixeGa naar voetnoot2) (savoir en me servant de cette équation-là, car la chose peut être accomplie beaucoup plus commodément par une autre voieGa naar voetnoot3)) et j'admirerai beaucoup votre methode si elle enseigne à trouver cette tangente presque sans aucun calcul et par la seule inspection des termes de l'équation’.
En réponse, de Sluse écrivit, le 6 octobreGa naar voetnoot4), que sa méthode avait, en effet, | ||||||||||||
[pagina 447]
| ||||||||||||
la portée que Huygens lui supposait et il ajouta, comme preuve, la construction de la tangente à la courbe en question. Or, quelques semaines après, probablement au commencement de décembreGa naar voetnoot5), Huygens apprit que Hudde était en possession d'une méthode semblable. Alors, ayant pris connaissance de l'algorithme employé par HuddeGa naar voetnoot6), Huygens ne tarda pas à en découvrir l'origine, qu'il exposa dans la lettre à de Witt de février 1663 dont nous avons déjà parléGa naar voetnoot7). En effet, on trouvera au § 6 de la Pièce No. VII (p. 516-517), ce que nous supposons être la première recherche instituée par Huygens sur le problème en question en partant de la méthode de Fermat. Elle lui fit connaître enfin la règle qu'il avait cherchée si ardemment. De plus, on rencontre sur les même pages du manuscrit de petits calculsGa naar voetnoot8) qui se rapportent à l'algorithme plus général de Hudde, dont celui de Huygens constitue un cas particulier. Ajoutons que Huygens communiqua sa méthode le 13 avril 1667 à l'Académie des Sciences dans un discours dont nous publierons le résumé dans un autre Tome, où nous réunirons tout ce qui concerne la participation de Huygens aux travaux de cette Académie. Enfin, en 1693, cette méthode fut publiée dans les ‘Divers ouvrages de Mathématiques et de Physique’Ga naar voetnoot9). À cette occasion Huygens ne manqua pas de constater la priorité de de Sluse et de Hudde dans l'invention de la règleGa naar voetnoot10). | ||||||||||||
[pagina 448]
| ||||||||||||
Notons encore que lors de la publication, en 1667, du troisième volume des ‘Lettres de Descartes’ éditées par ClerselierGa naar voetnoot1), et de celle, en 1679, des ‘Varia Opera’ de FermatGa naar voetnoot2), Huygens aperçutGa naar voetnoot3) que la théorie de la détermination des tangentes des courbes algébriques avait été poussée plus loin par Fermat et DescartesGa naar voetnoot4) qu'il ne l'avait su. S'il avait pu prendre connaissance également de la ‘Méthode de maximis et minimis expliquée et envoyée’ (en juin 1638) ‘par M. Fermat à M. Descartes’Ga naar voetnoot5), Huygens aurait vu que Fermat était en possession d'une méthode équivalente à la sienne pour trouver les tangentes d'une courbe algébrique quelconque f(x, y) = 0Ga naar voetnoot6) et qu'il l'avait appliquée, comme Huygens l'avait fait lui-même, et avec un succès égal, au folium de Descartes. | ||||||||||||
Les autres travaux mathématiques de 1661-1666.Nous avons encore à signaler quelques autres travaux de Huygens de moindre étendue que ceux nous venons d'analyser. Il y a en premier lieu la Pièce No. V de 1662 (p. 498-500) où Huygens déduit par voie géométrique d'une manière aussi simple qu'élégante, une | ||||||||||||
[pagina 449]
| ||||||||||||
équation cubique dont dépend la construction de l'heptagone régulier. Ensuite on a de cette même année la Pièce No. VI (p. 501-503) qui contient une quadrature et une cubature se rapportant à la courbe de Gutschoven et à un de ses solides de révolution. Puis, la Pièce No. VIII de 1664 (p. 518) nous fait connaître une méthode ingénieuse pour trouver le diamètre d'une surface sphérique appartenant à quelque objet, tandis que la Pièce No. IX de l'année suivante (p. 519-520) nous montre que Huygens a eu un instant l'idée de discuter l'équation générale du troisième degré en coordonnées cartésiennes, comme Descartes l'avait fait pour celle du deuxième degré. Enfin, il y a encore deux Pièces qui doivent dater de 1666. La première, | ||||||||||||
[pagina 450]
| ||||||||||||
No. VIII (p. 521-523) s'occupe d'un problème de l'analyse indéterminée du premier degré, problème qui trouve son application dans la science de la chronologie, lorsqu'il s'agit de déterminer l'année du Cycle Julien introduit par Joseph Justus Scaliger. Dans la deuxième (p. 524) Huygens vérifie une quadrature approchée du cercle, proposée par un certain Oudart. |
| |||||||||||