Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 248]

Troisième réponse¹⁾.
A l' ἘΞΈΤΑΣΙΣ du très-savant seigneur Chrétien Huygens¹⁾.

1. Après avoir expliqué ce qui semblait appartenir à la première Quadrature²⁾ je n'ai pas voulu, très-savant Seigneur, que cette mienne étude manquât à Vous, ou fût exigée par d'autres, auxquels le silence de l'auteur pût sembler une confession tacite d'erreur: et quoique, après ce qui a été dit par moi dans les pages précédentes, la réfutation de ce que vous écrivez longuement dans tout votre examen de la Cyclométrie soit facile, j'ai à dessein voulu la différer jusqu' ici afin de soumetre aux yeux de mes lecteurs, sans interruption, toute votre Ἐξέτασις et en même temps ma réponse.

2. En premier lieu donc vous dites pag. 25³⁾: Il (Grégoire de Saint Vincent) proposa quatre modes pour carrer le Cercle, et même en appliqua aussi à la quadrature de l'Hyperbole un, au sujet duquel, par plusieurs indices, on peut conclure qu'il fut estimé par lui-même meilleur que les autres. Un de ces indices est justement qu'il démontra par ce même mode deux quadratures de figures différentes, un autre que ce mode est beaucoup plus évident que les trois autres et par cela même devrait paraître beaucoup moins sujet à erreur; puis encore jusqu' à certain point en ce qu' il le produisit en premier lieu; enfin le plus fort indice consiste en ceci que, dans ce qu' il dit dans la préface au lecteur laquelle précède l'ouvrage entier, là où il expose brièvement l'histoire et le progrès de son invention, il ne mentionne aucun mode en dehors de ce seul. Il est vrai qu'il a pu avoir une autre raison de passer sous silence les trois quadratures suivantes, nommément qu'il savait que des mêmes principes toutes les quatre étaient déduites et démontrées.

Vous vous trompez, très savant Seigneur, et vos conjectures s'écartent aussi loin que possible de la vérité; la seule et unique raison de mettre en avant celle que l'Auteur appliqua en même temps au cercle et à l'hyperbole fut la proposition 50⁴⁾

1) La pièce est empruntée aux p. 120-124 de l'ouvrage d'Aynscom, cité dans la note 6, p. 210 du T. I. Pour faciliter les renvois, que nous aurons à faire, nous l'avons divisée en paragraphes.

1) La pièce est empruntée aux p. 120-124 de l'ouvrage d'Aynscom, cité dans la note 6, p. 210 du T. I. Pour faciliter les renvois, que nous aurons à faire, nous l'avons divisée en paragraphes.

2) Il s'agit du résumé de la première quadrature de Grégoire, lequel occupe la ‘Pars prima’ du ‘Lib. II’, p. 89-104 de l'ouvrage d'Aynscom. Comparez la p. 244 de l'‘Avertissement’ qui précède ici.

3) Voir la p. 315 du T. XI.

4) Dans cette proposition et la suivante Grégoire démontre que le volume du cylindre droit ayant pour base la figure CDIH de la p. 278 du Tome XI et pour hauteur AB est égal au volume du solide qu'on obtient en soumettant à l'opération ‘ducere planum in planum’ les aires GNIH, OPIH. Consultez, quant à la portée de ce théorème sur la première quadrature de Grégoire, les § 1-3 de l'‘Aperçu’ de cette quadrature, p. 277 du T. XI.

[p. 249]

Responsio III¹⁾.
Ad ἘΞΈΤΑΣΙΝ clariss. d. Christiani Hugenij.

1. Explanatis iis, quae ad primam quadraturam pertinere videbantur²⁾, nolui studium hoc meum, aut deesse Tibi Clariss. Domine, aut ab aliis requiri, quibus Auctoris silentium, tacita videri posset erroris confessio: & quamuis ex iis, quae in praecedentibus à me dicta sunt, facilis sit eorum refutatio, quae toto cyclometriae examine perscribis, studio tamen in hunc locum differre placuit, vt totam simul ᾽εξέταςιν tuam, vna cum responso, non interruptim oculis obiicerem.

2. Primum igitur pag. 25³⁾. quatuor, inquis, modos proposuit (Auctor) quadrandi circulum; vnum vero eorum, etiam quadraturae hyperboles applicauit: quem caeteris potiorem ab ipso existimari, ex multis indiciis colligere licet; vnum est hoc ipsum, quod duas diuersarum figurarum quadraturas, per eundem hunc demonstrarit: alterum, quod euidentior hic sit modus quam reliqui tres, ideoque minus errori obnoxius videri debuerit: & denique hoc maximum est, quod in iis quae ad lectorem in principio totius operis praefatur, vbi suae inuentionis historiam & progressum paucis exposuit, nullius modi praeter hunc vnum meminerit; potuit & aliam rationem habuisse tres posteriores quadraturas illic silentio praetereundi; eam videlicet, quod quatuor, omnes sciret ex iisdem principiis deductas, & demonstratas esse.

Falleris Clarissime Domine, & coniecturae illae tuae, quam longissimè à vero distant; sola & vnica ratio praeponendi illam, quam circulo simul & hyperbolae applicuit Auctor fuit propositio 50⁴⁾. quae, cum cylindrum ad aliud corpus non

1) La pièce est empruntée aux p. 120-124 de l'ouvrage d'Aynscom, cité dans la note 6, p. 210 du T. I. Pour faciliter les renvois, que nous aurons à faire, nous l'avons divisée en paragraphes.

2) Il s'agit du résumé de la première quadrature de Grégoire, lequel occupe la ‘Pars prima’ du ‘Lib. II’, p. 89-104 de l'ouvrage d'Aynscom. Comparez la p. 244 de l'‘Avertissement’ qui précède ici.

3) Voir la p. 315 du T. XI.

4) Dans cette proposition et la suivante Grégoire démontre que le volume du cylindre droit ayant pour base la figure CDIH de la p. 278 du Tome XI et pour hauteur AB est égal au volume du solide qu'on obtient en soumettant à l'opération ‘ducere planum in planum’ les aires GNIH, OPIH. Consultez, quant à la portée de ce théorème sur la première quadrature de Grégoire, les § 1-3 de l'‘Aperçu’ de cette quadrature, p. 277 du T. XI.

[p. 250]

laquelle puisqu'elle réduit d'une manière admirable le cylindre à un corps non cylindrique et ainsi est fondamentale à toutes les quadratures et ne pouvait être insérée parmi les autres sans troubler l'ordre, obligea de donner la première place à cette quadrature. De plus, c'est une très grave erreur que toutes les quadratures ont été déduites et démontrées par les mêmes principes, car en dehors de la réduction du cylindre circulaire au solide produit par deux paraboles, placées à la renverse l'une par rapport à l'autre⁵⁾, la première quadrature n'a rien de commun avec les autres. Le raisonnement dans les deux cas et la comparaison des solides et des rapports diffèrent du tout au tout; dans la première quadrature on ne fait aucun usage des proportionnalités; les autres ne peuvent être effectuées sans leur moyen; dans la première l'argumentation est conduite d'une manière nouvelle par la multiplication égale des rapports partiels⁶⁾, dans les autres aucune mention n'est faite de multiplication.

3. Vous continuez ensuite:⁷⁾ Mais il m'a semblé que l'une ou l'autre de ces considérations suffisait pour persuader, qu'il y aurait une seule discussion valable pour toutes laquelle, détruisant la première quadrature, entraîner ait les autres à sa suite. Car si nous avons montré qu'il y a erreur dans celle qui est la moins obscure, je ne vois pas pour quelle raison un meilleur succès se laisserait espérer pour les trois suivantes, qui se trouvent enveloppées des plus grandes ténèbres et que l'Auteur luimême semble mettre au-dessous de cette seule première.

Une double erreur est contenue dans ce peu de lignes; la première consiste en ce que vous estimez qu'une seule discussion suffit à toutes: or, comment une seule discussion pourrait-elle suffire à toutes, lorsque les trois dernières n'ont rien de commun avec la première? A supposer que votre ᾽εξέτασις, ce qu'elle a fait moins que toute autre chose, ait renversé la première, certainement elle ne se rapporte pas plus aux autres qu' à la dimension Archimédienne; si vous voulez l'essayer, vous corrigerez sur-le-champ votre jugement. L'autre erreur réside en ceci que vous croyez que la première quadrature a moins d'obscurité tandis que les suivantes sont couvertes des plus denses brouillards. Mais l'Auteur en juge tout autrement, moi, en les développant chacune pour soi, j'ai éprouvé toute autre chose. La première a certainement plus de complications et d'obscurité que les trois autres ensemble; dans ces dernières le raisonnement est très-clair et la réduction des solides facile, dans la première la nouvelle manière de comparer au moyen des rapports partiels également multipliés est compliquée, et la réduction des solides multiple, variée et très-difficile.

4. Pag. 26⁸⁾. Cependant je ne puis laisser de dire au moins ceci, que le trèssavant auteur n'a pas appliqué avec assez de bonheur quelques inventions en matière de proportionnalités aux quadratures et que, dans mon opinion, c'est là la cause de son erreur. C'est ce que j'avais observé tout premièrement dans la proposition 39 du livre 10 &c.

Ici, de nouveau, se présente une grave erreur: car ni dans 39, ni dans toute la

5) C'est-à-dire en appliquant l'opération ‘ducere planum in planum’, décrite au § 4, p. 278 du T. XI, à deux paraboles situées comme les paraboles ANZ et BPY de la figure de cette page 278.

6) Voir les §§ 7 et 9 à la p. 279 du T. XI en tenant compte de l'équivalence des termes ‘toties continere’ et ‘toties multiplicare’, sur laquelle on peut consulter la note 24, p. 246 du Tome présent.

7) Voir les p. 315-317 du T. XI.

8) Voir la p. 317 du T. XI.

[p. 251]

cylindricum, admirabili reducat modo, adeoque quadraturis omnibus esset fundamentalis, neque sine ordinis perturbatione, aliis inseri posset, primum huic quadraturae locum dedit. Porro quadraturas omnes ex iisdem principiis deductas, & demonstratas esse, error est longè grauissimus: nam praeter reductionem cylindri circularis, ad solidum ex ductu subalterno parabolarum ortum⁵⁾, nil prima cum caeteris commune habet: ratiocinatio in vtrisque, & solidorum, rationumque comparatio, toto differunt caelo. in hâc, nullus proportionalitatum vsus; illae, absque earum ope perfici non possunt: in hac, per rationes partiales aequemultiplicatas⁶⁾, nouo modo instituitur argumentatio, in illis, nulla multiplicationis mentio.

3. Pergis deinde⁷⁾: sed mihi vel alterutra harum considerationum sufficere visa est, vt persuaderet, vnam pro omnibus fore discussionem, quae quadraturam primariam infirmatura esset, reliquarum agmen ducentem: si enim erratum in ea ostenderimus, quae minus obscuritatis habet, non video quâ ratione melior successus expectandus sit in tribus sequentibus, quae maximâ caligine inuoluuntur, quasque auctor ipse vel vni illi posthabere videtur.

Duplex hic in tam paucis lineis error in teruenit; prior in hoc consistit; quod vnam omnibus sufficere discussionem existimes: quî enim discussio vna, sufficere possit omnibus, cum tribus reliquis nil cum prima sit commune? esto (quo nihil minus factum) primam euerterit ᾽εξέτασις tua, ad reliquas certè non magis illa, quam ad Archimedaeam pertinet dimensionem. experire si placet, & ilico iudicium ipse tuum corriges. alter in eo est, quod primam minus habere obscuritatis, sequentes autem maximâ inuolui putes caligine. at longè aliud de illis censet Auctor, aliud ego dum singulas explano, expertus sum. prima certè plus & tricarum & obscuritatis habet, quam reliquae simul omnes. in his & clarissima est ratiocinatio & reductio solidorum facilis; in illa nouus per rationes partiales aequemultiplicatas comparandi modus, intricatus est, & solidorum reductio multiplex, varia, ac perdifficilis.

4. Pag. 26⁸⁾. vnum tamen praetermittere nequeo quin dicam, Clariss. virum non satis feliciter quaedam inuenta in materia proportionalitatum ad quadraturam applicasse; atque hinc meâ opinione ipsi exstitisse erroris causam. primum omnium id in propos. 39. lib. 10. obseruaueram &c.

Grauis hîc rursum occurrit error: neque enim in 39, neque in tota prima qua-

5) C'est-à-dire en appliquant l'opération ‘ducere planum in planum’, décrite au § 4, p. 278 du T. XI, à deux paraboles situées comme les paraboles ANZ et BPY de la figure de cette page 278.

6) Voir les §§ 7 et 9 à la p. 279 du T. XI en tenant compte de l'équivalence des termes ‘toties continere’ et ‘toties multiplicare’, sur laquelle on peut consulter la note 24, p. 246 du Tome présent.

7) Voir les p. 315-317 du T. XI.

8) Voir la p. 317 du T. XI.

[p. 252]

première quadrature il n'est fait usage d'aucune proportionnalité, puisque c'est toute autre chose de comparer des rapports entre eux selon l'égale multiplication de leurs rapports, par lesquels ils sont constitués selon la huitième proposition du livre 10⁹⁾, que d'argumenter par proportionnalités: lisez la proposition 39, expliquée selon l'intention de l'Auteur¹⁰⁾ et comparez la avec la proposition 3 du livre suivant¹¹⁾ dont la démonstration est conduite par proportionnalités, et aussitôt apparaîtra une différence énorme: et, en effet, comment l'Auteur a-t-il pu appliquer moins heureusement à la Quadrature quelques inventions en matière de proportionnalités lors que ni dans la propos. 12¹²⁾ ou 39¹³⁾, ni dans 40 ou 44, ni dans 51 ou 52 ou 53, dans lesquelles toute la première quadrature est contenue, il ne cite ou n'emploie aucune proposition empruntée au livre des proportionnalités¹⁴⁾. Donc ce n'est pas de là qu' une cause d'erreur a pu exister pour l'auteur.

5. Pag. 27¹⁵⁾. je ramènerai la question à ceci que, à moins qu' il ne déclare impossible de conduire sa quadrature à bonne fin et de trouver par elle réellement une figure rectiligne égale au cercle, je lui montrerai de quelle manière cela pourrait ensuite être obtenu très facilement. Après cela en suivant ses propres pas je démontrerai, que, par la voie dans laquelle il nous a précédé jusqu' ici, on ne peut parvenir nullement à ce qu'il désire.

Sur la manière que vous promettez de donner par laquelle l'auteur pourrait dans la suite trouver très facilement une figure rectiligne égale au cercle nous verrons tantôt lorsque nous serons arrivés jusque-là. Qu'en suivant ses pas on peut arriver au but proposé sera démontré dans ce livre-ci et dans les suivants¹⁶⁾.

Ce qui suit jusqu' à la page 32¹⁷⁾ ne contient rien d'autre que quelques propotions de l'Auteur.

6. Pag. 32¹⁷⁾. Cela posé, il faut savoir que pour le savant auteur tout espoir et toute base de la quadrature à effectuer sont fondées en ceci qu'il estime facile de trouver le rapport du solide Hϒ¹⁸⁾ au solide XV (lequel rapport j' ai déjà dit être la seule

9) Comparez la note 8, p. 317 du T. XI où la même ‘Prop. 8’ est citée. D'ailleurs nous la reproduirons plus loin dans la note 28, p. 257.

10) Consultez, sur cette proposition 39, le § 10 de la p. 280 du T. XI et la note 8, p. 317 du même Tome. Ici il s'agit de l'explication que Aynscom a donnée de cette proposition à la p. 97 du ‘Lib. II’ de son ouvrage. D'après cette explication, pour autant qu'on peut la comprendre, Grégoire n'aurait voulu affirmer le ‘toties continere’ que pour les rapports ‘constituants’. Inutile de dire qu' alors elle perdrait tout l'intérêt que Grégoire y attache dans sa quadrature du cercle.

11) C'est-à-dire la ‘Prop. 3’ du ‘Lib. III’, p. 136 de l'ouvrage d'Aynscom (celui de Grégoire ne contient pas plus de dix livres), dans laquelle en effet, la conception du ‘toties continere’ ne joue aucun rôle.

12) Voici cette ‘Prop. 12’, p. 1105 de l'ouvrage de Grégoire: ‘Sint quatuor ordines quinque proportionalium A, B, C, D, E, & F, G, H, I, K: deinde L, M, N, O, P, & Q, R, S, T, V, habentium vltimas quantitates E, K, P, V aequales inter se. Dico rationem quantitatum AF ad LQ, toties continere rationem quantitatum CH ad NS, quoties ratio quantitatum CH ad NS, continet rationem quantitatum DI ad OT.’
Remarquons que d'après les propositions qui précèdent, dont nous en citerons deux dans la note 28, p. 257, les notations AF, LQ, etc. désignent A + F, L + Q, etc. Le théorème est donc faux, si du moins on attache aux mots leur signification ordinaire. Consultez là-dessus la note 28 citée.

13) Cette proposition et les cinq autres qui suivent ont toutes été mentionnées aux p. 277-280 du T. XI.

14) Il s'agit du ‘Liber octavus. De Proportionalitatibus Geometricis’, qui occupe lesp. 865-954 de l'ouvrage de Grégoire.

15) Voir la p. 319 du T. XI.

16) ")Il s'agit des ‘Lib. III, IV et V’ de l'ouvrage d'Aynscom qui traitent les trois autres quadratures de Grégoire.

17) Voir la p. 325 du T. XI.

17) Voir la p. 325 du T. XI.

18) Voir la figure de la page 254.

[p. 253]

dratura, vllus proportionalitatum vsus. quippe longè aliud est, rationes inter se comparare, secundum aequemultiplicationem illarum rationum, ex quibus iuxta octauam eiusdem lib. 10. constituuntur⁹⁾, aliud per proportionalitates argumentari: lege propos. 39. iuxta Auctoris mentem explicatam¹⁰⁾, illamque confer cum propos. 3. sequentis libri¹¹⁾, cuius demonstratio per proportionalitates instituitur; & ilico discrimen ingens apparebit: & vero quî Auctor potuit inuenta quaedam in materia proportionalitatum infelicius ad quadraturam applicasse, cum nec in propos. 12¹²⁾. aut 39¹³⁾. nec in 40 aut 44. nec in 51. aut. 52. aut 53. quibus tota prima continetur quadratura, vllam citet aut vllâ vtatur propositione ex libro de proportionalitatibus¹⁴⁾ petitâ? non igitur inde exstitisse Auctori potuit erroris causa.

5. Pag. 27¹⁵⁾. eo rem deducam, vt si quidem non impossible dicet quadraturam suam ad exitum perducere, & per eam reapse inuenire rectilineum circulo aequale, ostendam quî id facillimè imposterum assequatur: deinde vestigia ipsius insistens demonstrabo, quibus hactenus nobis praecessit, iis nequaquam ad optatum finem perueniri posse.

De modo quem daturum te polliceris quo facillimè imposterum Auctor rectilineum circulo inuenire possit aequale, mox videbo, vbi ad illum deuenero. porro vestigia illius insistendo ad optatum sinem deueniri posse hic, & sequentes edocebunt libri¹⁶⁾.

Quae sequuntur vsque ad pag. 32.¹⁷⁾ nil aliud continent, praeter aliquot Auctoris propositiones.

6. Pag. 32¹⁷⁾. his sic constitutis, sciendum est omnem spem & fundamentum perficiendae quadraturae, Clariss. viro in eo positum esse, quod existimet rationem solidi Hϒ¹⁸⁾ ad solidum XV (quam vnicam tantum desiderari iam monui) facilè

9) Comparez la note 8, p. 317 du T. XI où la même ‘Prop. 8’ est citée. D'ailleurs nous la reproduirons plus loin dans la note 28, p. 257.

10) Consultez, sur cette proposition 39, le § 10 de la p. 280 du T. XI et la note 8, p. 317 du même Tome. Ici il s'agit de l'explication que Aynscom a donnée de cette proposition à la p. 97 du ‘Lib. II’ de son ouvrage. D'après cette explication, pour autant qu'on peut la comprendre, Grégoire n'aurait voulu affirmer le ‘toties continere’ que pour les rapports ‘constituants’. Inutile de dire qu' alors elle perdrait tout l'intérêt que Grégoire y attache dans sa quadrature du cercle.

11) C'est-à-dire la ‘Prop. 3’ du ‘Lib. III’, p. 136 de l'ouvrage d'Aynscom (celui de Grégoire ne contient pas plus de dix livres), dans laquelle en effet, la conception du ‘toties continere’ ne joue aucun rôle.

12) Voici cette ‘Prop. 12’, p. 1105 de l'ouvrage de Grégoire: ‘Sint quatuor ordines quinque proportionalium A, B, C, D, E, & F, G, H, I, K: deinde L, M, N, O, P, & Q, R, S, T, V, habentium vltimas quantitates E, K, P, V aequales inter se. Dico rationem quantitatum AF ad LQ, toties continere rationem quantitatum CH ad NS, quoties ratio quantitatum CH ad NS, continet rationem quantitatum DI ad OT.’
Remarquons que d'après les propositions qui précèdent, dont nous en citerons deux dans la note 28, p. 257, les notations AF, LQ, etc. désignent A + F, L + Q, etc. Le théorème est donc faux, si du moins on attache aux mots leur signification ordinaire. Consultez là-dessus la note 28 citée.

13) Cette proposition et les cinq autres qui suivent ont toutes été mentionnées aux p. 277-280 du T. XI.

14) Il s'agit du ‘Liber octavus. De Proportionalitatibus Geometricis’, qui occupe lesp. 865-954 de l'ouvrage de Grégoire.

15) Voir la p. 319 du T. XI.

16) ")Il s'agit des ‘Lib. III, IV et V’ de l'ouvrage d'Aynscom qui traitent les trois autres quadratures de Grégoire.

17) Voir la p. 325 du T. XI.

17) Voir la p. 325 du T. XI.

18) Voir la figure de la page 254.

[p. 254]

chose qui reste à désirer) dès que l'on connaît les deux rapports suivants, savoir celui du solide MΞ au solide ΛΣ, et celui du solide KΘ au solide ΔΓ. Car alors on



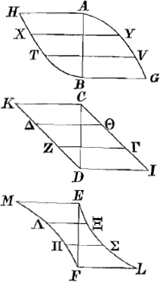pourra argumenter comme il suit. Connu est le rapport du solide MΞ au solide ΛΣ, de même celui du solide KΘ au solide ΔΓ; donc est connu aussi combien de fois le premier rapport contient le dernier, or, autant de fois que celui-là contient celui-ci, autant de fois ce dernier, c'est-à-dire le rapport du solide KΘ au solide ΔΓ contient le rapport du solide Hϒ à XV, donc aussi ce dernier rapport sera connu.

Ici vous vous écartez tout à fait du sens de l'auteur; car quoique le fondement de la quadrature à effectuer soit situé en ceci que l'on fasse connaître le rapport du solide HY au solide XV, jamais l'auteur n'a estimé qu'il fût facile à trouver lorsque sont connus les rapports du solide MΞ au solide ΔΣ et du solide KΘ au solide ΔΓ; car il les avait déjà fait connaître auparavant par la propos. 43¹⁹⁾; d'où il suit qu'il ne s'est pas aussi servi de l'argumentation que vous dites, mais de celle que j'ai produite dans le Scholium à la proposition 40²⁰⁾ laquelle du tout au tout diffère de la vôtre; de plus, vouloir admettre comme généralement connu un troisième rapport lorsque de deux rapports connus le premier contient par multiplication le second autant de fois que celui-ci contient par multiplication le troisième est la même chose que de vouloir produire entre deux données un nombre quelconque de moyennes proportionnelles²¹⁾: or, il serait insensé de confondre la quadrature avec le mésolabe ou de supposer celui-ci pour accomplir celle-là; l'auteur n'a donc pas espéré rendre connu un troisième rapport au moyen de deux rapports connus dont le premier contient autant de fois le second, que ce second le troisième²²⁾.

7. Ibid.²³⁾ Si donc je lui aurai indiqué quel est le rapport du solide MΞ au solide ΛΣ, et aussi quel est le rapport du solide KΘ au solide ΔΓ, et que même alors il ne puisse dire quel est le rapport du solide Hϒ au solide XV, il devra avouer qu'il a tenté en vain la quadrature tant du Cercle que de l'Hyperbole.

19) Comparez le § 8, p. 279 du T. XI.

20) Voir, sur la ‘Prop. 40’ du ‘Lib. 10’, le § 10, p. 280 du T. XI. Aux p. 98-103 de son ouvrage Aynscom fait suivre cette proposition par une explication ‘iuxta auctoris mentem’ et par un ‘Scholium’ prolixe et diffus. Il y prétend que l'assertion de Grégoire: que le rapport des solides MΞ et ΛΣ (voir la figure de la page présente) doit contenir autant de fois le rapport des solides KΘ et ΔΓ que celui-ci contient le rapport des solides HY et XV, ne s'applique pas aux rapports ‘totaux’ des solides entiers, mais seulement aux rapports ‘partiels’, qui constituent ces rapports totaux, c'est-à-dire, aux rapports des tranches infiniment petites, pour lesquels, en effet, l'assertion est vraie. Ensuite pour représenter ces rapports partiels il a recours aux aires hyperboliques que nous avons mentionnées dans la note 24, p. 245 du Tome présent; mais il finit par commettre la faute même contre laquelle il avertit le lecteur au début, en appliquant à des sommes ce qu' il n'a démontré que pour leurs parties. De plus, il fait la supposition erronée que le rapport des aires hyperboliques DEGF et GFHC (voir la figure de la note 24 que nous venons de citer) sera rationnel quand il en est ainsi des rapports des longueurs DE, FG et HC. Et, nonobstant tout cela, il n'arrive à aucune conclusion bien définie, qui permettrait de déduire le troisième rapport des deux autres par la construction ou par le calcul.

21) Soient a : b, c : d, e : f les trois rapports en question. Si alors on a a : b = (c : d)ⁿ et en même temps c : d = (e : f)ⁿ, où n est un nombre commensurable, la détermination du rapport e : f se réduit, en effet, au mésolabe, c'est-à-dire, à la construction d'un certain nombre de proportionnelles entre deux segments donnés, pourvu du moins qu'il soit possible de trouver le nombre n au moyen de la première relation, où les rapports a : b et c : d sont supposés connus.
Pour le montrer posons e : f = g : d = (c : d)^{λ : μ}. On a alors ; donc le segment g est la λ^ième des μ - 1 proportionelles à interpoler entre d et c.

22) Ici la confusion, créée non sans intention, à ce qu' il nous semble, est à son comble. En vérité, si l'on nie que Grégoire ait voulu indiquer comment on pouvait déterminer le troisième rapport à l'aide des deux autres, alors sa première quadrature s'évanouit entièrement; puisqu' il ne donne aucun autre moyen pour parvenir à ce troisième rapport dont sa quadrature du cercle dépend.

23) Voir le quatrième alinéa de la p. 325 du T. XI.

[p. 255]

inueniri posse, si cognitae sint duae rationes nimirum ratio solidi MΞ ad sol. ΛΣ & ratio sol. KΘ ad sol ΔΓ. sic enim tunc argumentabitur: nota est ratio solidi MΞ ad sol. ΛΣ, item ratio solidi KΘ ad sol. ΔΓ, ergo notum quoque, quoties illa ratio hanc continet; quoties autem illa hanc continet, toties haec ipsa continet rationem solidi Hϒ aa sol. XV, ergo & haec nota erit.

Plane hic ab Auctoris mente deuias; licet enim fundamentum perficiendae quadraturae in ea positum sit, vt nota reddatur ratio solidi HY ad sol. XV, nunquam tamen existimauit Auctor illam facilè inueniri posse, si cognitae forent duae rationes, nimirum solidi MΞ ad sol. ΛΣ & sol. KΘ ad sol. ΔΓ; has enim antea notas fecerat propos. 43¹⁹⁾. vnde nec illam quam profers argumentationem instituet, sed eam, quam in scholio ad propos. 40. attuli²⁰⁾, quae toto caelo à tua differt: porro ex datis vel notis duabus rationibus, quarum prima toties per multiplicationem continet secundam, quoties haec per multiplicationem continet tertiam, velle tertiam vniuersaliter notam facere, idem est atque inter duas datas, quotcumque medias proportionales velle exhibere²¹⁾: stultum autem foret quadraturam meselabio commiscere, aut hoc ad illam perficiendam supponere. non igitur ex duabus notis rationibus, quarum prima toties multiplicat secundam, quoties haec multiplicat tertiam, sperauit Auctor hanc notam reddere²²⁾.

7. Ibid.²³⁾ si igitur indicauero ipsi, quae sit ratio solidi MΞ ad sol. ΛΣ, item quae sit solidi KΘ ad sol. ΔΓ, & ne tum quidem dicere possit, quam rationem habeat solidum Hϒ ad sol. XV, fateatur sanè se frustra vtramque quadraturam tentasse, tum circuli tum hyperboles.

19) Comparez le § 8, p. 279 du T. XI.

20) Voir, sur la ‘Prop. 40’ du ‘Lib. 10’, le § 10, p. 280 du T. XI. Aux p. 98-103 de son ouvrage Aynscom fait suivre cette proposition par une explication ‘iuxta auctoris mentem’ et par un ‘Scholium’ prolixe et diffus. Il y prétend que l'assertion de Grégoire: que le rapport des solides MΞ et ΛΣ (voir la figure de la page présente) doit contenir autant de fois le rapport des solides KΘ et ΔΓ que celui-ci contient le rapport des solides HY et XV, ne s'applique pas aux rapports ‘totaux’ des solides entiers, mais seulement aux rapports ‘partiels’, qui constituent ces rapports totaux, c'est-à-dire, aux rapports des tranches infiniment petites, pour lesquels, en effet, l'assertion est vraie. Ensuite pour représenter ces rapports partiels il a recours aux aires hyperboliques que nous avons mentionnées dans la note 24, p. 245 du Tome présent; mais il finit par commettre la faute même contre laquelle il avertit le lecteur au début, en appliquant à des sommes ce qu' il n'a démontré que pour leurs parties. De plus, il fait la supposition erronée que le rapport des aires hyperboliques DEGF et GFHC (voir la figure de la note 24 que nous venons de citer) sera rationnel quand il en est ainsi des rapports des longueurs DE, FG et HC. Et, nonobstant tout cela, il n'arrive à aucune conclusion bien définie, qui permettrait de déduire le troisième rapport des deux autres par la construction ou par le calcul.

21) Soient a : b, c : d, e : f les trois rapports en question. Si alors on a a : b = (c : d)ⁿ et en même temps c : d = (e : f)ⁿ, où n est un nombre commensurable, la détermination du rapport e : f se réduit, en effet, au mésolabe, c'est-à-dire, à la construction d'un certain nombre de proportionnelles entre deux segments donnés, pourvu du moins qu'il soit possible de trouver le nombre n au moyen de la première relation, où les rapports a : b et c : d sont supposés connus.
Pour le montrer posons e : f = g : d = (c : d)^{λ : μ}. On a alors ; donc le segment g est la λ^ième des μ - 1 proportionelles à interpoler entre d et c.

22) Ici la confusion, créée non sans intention, à ce qu' il nous semble, est à son comble. En vérité, si l'on nie que Grégoire ait voulu indiquer comment on pouvait déterminer le troisième rapport à l'aide des deux autres, alors sa première quadrature s'évanouit entièrement; puisqu' il ne donne aucun autre moyen pour parvenir à ce troisième rapport dont sa quadrature du cercle dépend.

23) Voir le quatrième alinéa de la p. 325 du T. XI.

[p. 256]

Vous auriez pu, croyez moi, vous épargner ce labeur, car le rapport du solide MΞ au solide ΛΣ et de même du solide KΘ au solide ΔΓ lui était connu et il l'avait démontré tant à Rome qu'en Belgique à d'autres, plusieurs années avant que vous n'aviez vu le jour: lisez la propos. 43, livre 10, qui fait connaître les deux rapports; vous n'aviez donc nullement besoin de les indiquer à un Auteur, duquel même vous les aviez pris.

Si²⁴⁾, au contraire, lorsque ces deux rapports sont donnés, il aurait pu trouver ensuite celui du solide Hϒ au solide XV, alors il peut croire avoir réellement carré le Cercle.

C'est ici cette manière de réduire très facilement le cercle à un carré, que vous avez promise à la page 27¹⁵⁾ de donner à l'Auteur. Je vous prie, très-savant Seigneur, d'où avez vous pris que la quadrature est effectuée lorsque le rapport du solide HY au solide XV est connu? Certainement d'aucun autre que de l'Auteur et même si vous le vouliez, vous ne pourriez le nier: mais comment alors l'enseignez vous, comme s'il l'ignorait, à celui même duquel vous l'avez appris? Je voudrais qu'en écrivant de telles choses vous vous fussiez rappelé ce que et à qui vous écriviez.

Je dirai²⁵⁾ maintenant quels sont ces rapports. Quant au premier, savoir celui du solide MΞ au solide ΛΣ, je dis qu'il est le même que celui des nombres 53 à 203, tandis que l'autre, le rapport du solide KΘ au solide ΔΓ est celui de 5 à 11 et de ces deux rapports je donnerai plus loin la démonstration &c. Par conséquent, il lui incombera maintenant de définir combien de fois le premier rapport contient le second, c'est-à-dire combien de fois le rapport de 53 à 203 contient le rapport 5 à 11. Mais d'abord comment va-t-il expliquer ici le terme contenir? &c.

Je n'ai aucune objection à ce que le rapport du solide MΞ au solide ΛΣ est le même que celui des nombres 53 à 203 et l'autre du solide KΘ au solide ΔΓ celui de 5 à 11, pourvu que l'un et l'autre soient bien démontrés: mais combien de fois le premier rapport contient par multiplication le second se trouve défini dans le scholium de la proposition 40 d'après les seuls principes de l'Auteur: mais dans quel sens le mot continere doit être expliqué c'est ce qu' on peut voir dans le scholium et les propositions 39.40 précédemment expliquées, d'où il suit que c'est contre la vérité, ce qui est prétendu à la page 37²⁶⁾, que dans l'opus Geometricum il n'est pas donné aucune autre explication du mot continere en dehors des deux produites par vous; et je m'étonne en vérité que cette interprétation n'a pas été aperçue par vous, parce qu'elle pouvait facilement être comprise de la proposition 12²⁷⁾; laquelle repose sur la huitième, surtout en y ajoutant l'explication du Père Sarasa au corollaire 9²⁸⁾ des confirmations de la quadrature, livre qui n'a pas

24) Voir le cinquième alinéa de la p. 325 du T. XI.

15) Voir la p. 319 du T. XI.

25) Voir les p. 325 et 327 du T. XI, à commencer par l'avant-dernier alinéa de la p. 325.

26) Voir le deuxième alinéa de la p. 329 du T. XI.

27) Voir la note 12; puisque la proposition est erronée, il était difficile d'en déduire le sens véritable du terme ‘continere’.

28) Dans le corollaire en question (p. 32 de son ouvrage) de Sarasa s'efforce de sauver la ‘Prop. 12’ mentionnée en expliquant les étranges sous-entendus qu'on doit supposer pour comprendre la portée des propositions de Grégoire. En effet, ces sous-entendus sont bien propres à déconcerter celui qui consulte l'ouvrage de Grégoire. Ainsi l'addition des rapports représente chez lui deux opérations différentes qu'il discute amplement dans le ‘Scholion’ à la ‘Prop. 6’ du ‘Lib. 10’ (p. 1102-1103 de son ouvrage). De cette façon il lui arrive de formuler des propositions étonnantes telle que la ‘Prop. 8’, p. 1104 du même ‘Lib. 10’, que nous citons, avec sa démonstration, comme échantillon. Disons d'abord que A, B, C, D sont des segments de droites de longueurs arbitraires et que AB signifie la somme des segments A et B.
Voici donc cette proposition: ‘Sint iam rationes AB ad CD, termini tam antecedens quàm consequens diuisi, & antecedens quidem in A & B, consequens verò in C & D. Dico rationem AB ad CD, eandem esse cum ratione A ad C, B ad C, item A ad D, B ad D.
Demonstratio. Ratio A ad C, addita rationi B ad C, aequalis est rationi AB ad C (per 114 de proport.). Item ratio A ad D, addita rationi B ad D, aequalis est rationi AB ad D. Itaque cùm ratio AB ad C, vnà cum ratione AB ad D, aequalis sit rationi AB ad CD per praec. patet rationem AB ad CD, aequari rationibus A ad C, B ad C, vnà cum rationibus A ad D, & B ad D’.
Quant à la proposition précédente, sur laquelle la démonstration s'appuie, elle est comme il suit:
‘Propositio VII. Sit rationis A ad BC consequens divisum in B & C. Dico rationem A ad totam BC, eandem esse cum ratione A ad B, & A ad C’.

[p. 257]

Supersedere, mihi crede, labori isti poteras; rationem enim solidi MΞ ad sol. ΛΣ, item solidi KΘ ad sol. ΔΓ, notam habuit, aliisque & Romae & in Belgio demonstrauit Auctor, pluribus annis antea, quam tu vita & luce fruereris: lege propos. 43. lib. 10. quae utramque rationem notam facit; nil igitur opus erat illam Auctori indicare, ex quo solo notitiam illius hausisti.

Sin²⁴⁾ vero datis istis duabus rationibus, inuenire post hac potuerit rationem solidi Hϒ ad sol. XV, tum se credat circulum reuera quadrasse.

Hic ille modus est circulum facillimè ad quadrum reducendi, quem pag. 27.¹⁵⁾ daturum te auctori pollicitus es: Quaeso te Clariss. Domine, vnde habes, notâ ratione solidi HY ad sol. XV, quadraturam absolui? non aliundè certè quam ex Auctore, neque id, si velis, diffiteri potes: vt quid igitur, acsi hunc ignoraret is à quo solo didicisti, quadraturae modum prescribis? cum illa scriberes, optassem meminisse te, quid, & cui scriberes.

Dicam²⁵⁾ autem nunc ipsas rationes: & primam quidem, hoc est rationem solidi MΞ ad sol. ΛΣ, aio esse eandem quae numeri 53 ad 203. alteram vero rationem solidi KΘ ad sol. ΔΓ, eam quae 5 ad 11. atque horum vtrumque infra sum demonsratus &c. consequenter hoc nunc definiendum ei incumbet, quoties ratio harum prima, contineat secundam, hoc est quoties ratio 53 ad 203, contineat rationem 5 ad 11. sed enim quo sensu verbum continere hîc explicaturus est? &c.

Rationem solidi MΞ ad sol. ΛΣ eandem esse quae numeri 53. ad 203. & alteram solidi KΘ ad sol. ΔΓ, eam quae 5. ad 11. nil habeo quod opponam, cum vtrumque rectè demonstratum sit: quoties autem ratio prima per multiplicationem contineat secundam, definitum est in scol. ad propos. 40. ex solis Auctoris principiis: quo autem sensu verbum continere explicaturus sit, vide idem scholium & propos. 39. 40. ante explicatas. vnde à vero alienum est, quod pag. 37. asseritur²⁶⁾, aliam interpretationem verbi continere, praeter duas à Te allatas, nullam in oper. Geom. exhiberi. & vero miror, interpretationem illam à Te perceptam non esse, cum ex prop. 12.²⁷⁾ quae octauae innititur, facile intelligi potuerit, additâ praesertim explicatione P. Sarassae coroll. 9.²⁸⁾ confirmartionum quadraturae, qui liber deesse

24) Voir le cinquième alinéa de la p. 325 du T. XI.

15) Voir la p. 319 du T. XI.

25) Voir les p. 325 et 327 du T. XI, à commencer par l'avant-dernier alinéa de la p. 325.

26) Voir le deuxième alinéa de la p. 329 du T. XI.

27) Voir la note 12; puisque la proposition est erronée, il était difficile d'en déduire le sens véritable du terme ‘continere’.

28) Dans le corollaire en question (p. 32 de son ouvrage) de Sarasa s'efforce de sauver la ‘Prop. 12’ mentionnée en expliquant les étranges sous-entendus qu'on doit supposer pour comprendre la portée des propositions de Grégoire. En effet, ces sous-entendus sont bien propres à déconcerter celui qui consulte l'ouvrage de Grégoire. Ainsi l'addition des rapports représente chez lui deux opérations différentes qu'il discute amplement dans le ‘Scholion’ à la ‘Prop. 6’ du ‘Lib. 10’ (p. 1102-1103 de son ouvrage). De cette façon il lui arrive de formuler des propositions étonnantes telle que la ‘Prop. 8’, p. 1104 du même ‘Lib. 10’, que nous citons, avec sa démonstration, comme échantillon. Disons d'abord que A, B, C, D sont des segments de droites de longueurs arbitraires et que AB signifie la somme des segments A et B.
Voici donc cette proposition: ‘Sint iam rationes AB ad CD, termini tam antecedens quàm consequens diuisi, & antecedens quidem in A & B, consequens verò in C & D. Dico rationem AB ad CD, eandem esse cum ratione A ad C, B ad C, item A ad D, B ad D.
Demonstratio. Ratio A ad C, addita rationi B ad C, aequalis est rationi AB ad C (per 114 de proport.). Item ratio A ad D, addita rationi B ad D, aequalis est rationi AB ad D. Itaque cùm ratio AB ad C, vnà cum ratione AB ad D, aequalis sit rationi AB ad CD per praec. patet rationem AB ad CD, aequari rationibus A ad C, B ad C, vnà cum rationibus A ad D, & B ad D’.
Quant à la proposition précédente, sur laquelle la démonstration s'appuie, elle est comme il suit:
‘Propositio VII. Sit rationis A ad BC consequens divisum in B & C. Dico rationem A ad totam BC, eandem esse cum ratione A ad B, & A ad C’.

[p. 258]

pu vous manquer, vu un si grand voisinage des lieux et qu' il a paru deux années avant le vôtre²⁹⁾.

8. Pag. 37³⁰⁾. il n'a donc pas enseigné la maniere de déterminer combien de fois le rapport du solide MΞ au solide ΛΣ contienne le rapport du solide KΘ au solide ΔΓ et par conséquent ne pourrait pas non plus déterminer combien de fois ce rapport contient le rapport du solide Hϒ au solide XV. D'où il paraît que ce rapport, même alors que les deux premiers sont donnés, ne peut être connu au moyen de ce que le très-savant auteur a trouvé, et que par conséquent il a espéré en vain de pouvoir effectuer de cette manière la quadrature du cercle.

Ici est commise une erreur capitale, qui montre aussi que vous n'entendez pas la doctrine de l'auteur, car soit que vous preniez le mot continere dans le sens voulu par l'auteur et par moi précédemment expliqué, soit que vous y voyiez un continere par multiplication il a abondamment enseigné les deux modes de détermination comme il est démontré dans le scholium de la proposition 40. du livre 10 de l'opus Geometricum³¹⁾, d'où ce troisième rapport pouvait devenir connu par les inventions de l'auteur, de sorte qu'il n'a pas espéré en vain d'effectuer par cette voie la quadrature du cercle.

Il³²⁾ ne me reste maintenant que de rendre manifeste ce que j'ai posé dans ce qui précède, en disant que je démontrerais que le solide MΞ est au solide ΛΣ comme 53 à 203, et de même que le solide KΘ aurait au solide ΔΓ le même rapport que 5 à 11. Mais comme pour démontrer le premier il est nécessaire que nous sachions quel est le rapport de l'onglet parabolique à son cylindre de même base et de même hauteur; à cet effet faisant connaître ce rapport, nous allons augmenter le traité que le très-Savant Auteur donne sur cet onglet, dans la partie 5 du livre 9, d'un Théorème excellent, lequel je m'étonne que l' Auteur n'a pas trouvé lui-même parce qu'il se déduit facilement des choses qu'il avait déjà démontrées, ainsi qu'il paraîtra bientôt.

Vous vous trompez, très-Savant Seigneur, l'Auteura vu et inventé ce Théorème il y a déjà trente ans et plus, mais comme celui-ci pouvait à tel point sans peine aucune se déduire de ce qu'il avait démontré, il ne l'a jugé digne que d'un corollaire et non pas d'une proposition. Voyez le corollaire³³⁾ de la proposition 99 du livre 9 de l'opus Geometricum où vous lisez ces mots: De là est manifeste

29) L'ouvrage de Sarasa, cité p. 156, note 7 du T. I, parut à Anvers en 1649; il porte en haut des pages la suscription ‘Confirmationes quadraturae’.

30) Voir le second alinéa de la p. 329 du T. XI.

31) Il s'agit toujours du ‘Scholium’, ajouté par Aynscom à la ‘Prop. 40’ du ‘Lib. 10’, laquelle dans l'ouvrage de Grégoire n'est pas pourvu d'un ‘Scolium’. Consultez la note 20, p. 254 du Tome présent.

32) Voir la p. 329 du T. XI à commencer par le troisième alinéa.

33) Voici le ‘Corollarium’ en question qu'on trouve à la p. 1034 de l'ouvrage de Grégoire: ‘Hinc manifesta est ratio dignoscendi proportionem inter vngulam parabolicam, & cylindrum parabolicum qui vngulam continet, vel inter vngulam & residuum quod cum vngula parabolica cylindrum perficit. ex libro etenim quem praemisimus de parabola methodus colligi potest reducendi cylindrum parabolicum ad parallelepipedum illi aequale; cum verò hac praesenti propositione praxis demonstrata sit etiam vngulam ad parallelepipedum reducendi, quod eidem sit aequale: qui horum parallelepipedorum rationem cognouerit, etiam proportiones cognitas habebit, quae sunt inter cylindrum parabolicum eiusque vngulam’.

[p. 259]

Tibi non poterat, in tanta locorum vicinitate, cum duobus annis ante tuum prodierit²⁹⁾.

8. Pag. 37.³⁰⁾ non docuit igitur modum determinandi, quoties ratio solidi MΞ ad sol. ΛΣ, contineat rationem sol. KΘ ad sol. ΔΓ, ac proinde nec determinari poterit, quoties haec ratio contineat rationem solidi Hϒ ad solidum XV: quare liquet hanc rationem ne duabus quidem prioribus datis, per inuenta Clariss. viri cognosci posse, adeoque frustra ipsum sperasse hoc modo perficere circuli quadraturam.

Hic error commissus est palmaris, qui etiam in Auctoris doctrina peregrinum Te ostendit: siue enim verbum continere sumas in sensu ab Auctore intento & ante à me explicato, siue per illud intelligas continentiam per multiplicationem, vtrumque determinandi modum, abunde docuit vt ostensum in schol. ad propos. 40. lib. 10. oper. Geom.³¹⁾ vnde tertia illa ratio per inuenta Auctoris nota fieri potuit, adeoque non frustra hâc viâ sperauit circuli quadraturam perficere.

Restat³²⁾ nunc tantum vt manifesta faciam, quae in praecedentibus posita fuere. dixi enim me demonstraturum, quod solidum MΞ esset ad sol. ΛΣ, vt 53 ad 203, item quod solidum KΘ, rationem haberet ad solidum ΔΓ, quam 5 ad 11. quoniam autem ad horum primi demonstrationem necessarium est, vt notum habeamus, quae sit ratio vngulae parabolicae ad cylindrum suum, idcirco hanc rationem declarantes, tractatum Clar. viri quem de eadem vngula proposuit, vno egregio Theoremate auctiorem reddemus; quod miror ipsum non inuenisse, cum ex iis quae iam ostenderat facili negotio deducatur.

Falleris Clariss. Domine, Theorema illud & vidit & inuenit Auctor iam à triginta & quod excedit, annis: sed quia tam nullo negotio ex iis quae demonstrarat deduci poterat, corollario illud, non propositione dignatus est. Inspice corollarium³³⁾ propos. 99. lib. 9. oper. Geom. in quo haec verba leges: Hinc manifesta est ratio dignoscendi proportionem inter vngulam parabolicam & cylindrum, qui

29) L'ouvrage de Sarasa, cité p. 156, note 7 du T. I, parut à Anvers en 1649; il porte en haut des pages la suscription ‘Confirmationes quadraturae’.

30) Voir le second alinéa de la p. 329 du T. XI.

31) Il s'agit toujours du ‘Scholium’, ajouté par Aynscom à la ‘Prop. 40’ du ‘Lib. 10’, laquelle dans l'ouvrage de Grégoire n'est pas pourvu d'un ‘Scolium’. Consultez la note 20, p. 254 du Tome présent.

32) Voir la p. 329 du T. XI à commencer par le troisième alinéa.

33) Voici le ‘Corollarium’ en question qu'on trouve à la p. 1034 de l'ouvrage de Grégoire: ‘Hinc manifesta est ratio dignoscendi proportionem inter vngulam parabolicam, & cylindrum parabolicum qui vngulam continet, vel inter vngulam & residuum quod cum vngula parabolica cylindrum perficit. ex libro etenim quem praemisimus de parabola methodus colligi potest reducendi cylindrum parabolicum ad parallelepipedum illi aequale; cum verò hac praesenti propositione praxis demonstrata sit etiam vngulam ad parallelepipedum reducendi, quod eidem sit aequale: qui horum parallelepipedorum rationem cognouerit, etiam proportiones cognitas habebit, quae sunt inter cylindrum parabolicum eiusque vngulam’.

[p. 260]

la manière de reconnaître le rapport entre l'onglet parabolique et le cylindre qui contient l'onglet, ou entre l'onglet et le reste du cylindre, etc. et je m'étonne grandement que vous ne l'avez pas lu, ou, si vous l'avez lu, de l'avoir dissimulé.

Du reste, avec tout votre examen de la Cyclométrie vous n'avez fait autre chose que de montrer que de deux rapports connus dont le premier multiplie le second autant de fois que ce dernier multiplie un troisième, ce troisième, par les inventions que l'Auteur a appliquées à la première quadrature, ne devient pas connu. Mais l'Auteur procède par une voie tout à fait différente et par conséquent n'a nullement eu l'intention de saire connaître de deux rapports également multipliés un troisième, parce que la solution de ceci dépend du mésolabe. Il est donc manifeste que votre ἐξέτασις non seulement ne renverse pas la première quadrature de l'Auteur mais même ne la touche pas.

Cependant digne de louange est votre effort, par lequel vous avez avec plus de diligence que de succès tenté une chose ardue³⁴⁾. Ce n'est pas de peu d'importance que parmi tant d'excellents géomètres de ce siècle, vous, entre les premiers, vous vous avez choisi cette tâche. Qu' une autre fois cette étude, si vous avez le loisir de vous y appliquer, oblige l'Auteur et moi d'un nouveau bénéfice.

34) Allusion à la phrase qui suit, employée par Huygens dans la préface de l'ouvrage jumeau qui contient l'Ἐξἐτασις: ‘intellexi tandem, majori subtilitate quàm successu rem arduam tentatam fuisse’. Voir la p. 287 du T. XI.

[p. 261]

vngulam continet; vel inter vngulam & residuum cylindri &c. atque hoc miror valdè, aut non legisse Te aut si legeris dissimulasse.

Caeterum cum toto Cyclometriae examine nil aliud egeris, quam ostendere quod ex notis duabus rationibus, quarum prima toties multiplicat secundam, quoties haec multiplicat tertiam, per auctoris inuenta, quae primae adhibuit quadraturae, tertia non innotescat, Auctor vero toto caelo diuersâ incedat viâ, adeoque ex duabus notis rationibus aequimultiplicatis, nullo modo intenderit tertiam notam facere, quia illius solutio dependet à meselabio, manifestum est ᾽εζἑταςιν tuam, non solum primam Auctoris quadraturam non euertere, sed illam ne quidem impetere.

Laude tamen dignus est conatus tuus, quo licet maiori diligentia quam successu rem arduam tentaueris³⁴⁾, non exiguum est tot inter eximios hoc aeuo geometras, Te primos inter, hanc Tibi prouinciam delegisse. quod rursus studium, adhibere si vacet, & Auctorem & me nouo affeceris beneficio.

34) Allusion à la phrase qui suit, employée par Huygens dans la préface de l'ouvrage jumeau qui contient l'Ἐξἐτασις: ‘intellexi tandem, majori subtilitate quàm successu rem arduam tentatam fuisse’. Voir la p. 287 du T. XI.