Oeuvres complètes. Tome IV. Correspondance 1662-1663

[p. 468]

N^o 1184.
Is. de la Peyrere à Christiaan Huygens.
[décembre 1663].
Appendice II au No. 1182.

La lettre se trouve à Leiden, coll. Huygens.

Problema¹⁾.

Duabus datis rectis lineis, duas medias proportionales inuenire. Oportet autem vt ratio maioris datae ad minorem datam, non sit maior duplâ.

Sint datae duae lineae, AB et CD. AB maior. CD minor. Quibus inueniendae sunt duae mediae proportionales.

Ducatur linea EF. Sumaturque in eâ GH, aequalis maiori datae AB: et GI aequalis minori datae CD. Auferatur ex GH, GK aequalis GI. Eritque residuum KH, differentia quâ GH excedit GI. Diuidatur differentia KH in duas partes aequales KL, et LH. Addaturque LH toti GH: ita vt HM aequalis fiat LH. Constituaturque vna diameter MI, ex tribus adunatis lineis, IG, GH et HM. Describatur circa diametrum MI, circulus MNIO. Seceturque diameter ad angulos rectos in puncto G, per lineam ON circulo inscriptam. Inueniatur GP, media proportionalis duabus GM et GN. Inscribatur media GP inuenta, a puncto G, ad punctum P, in portione circuli MN. Extendaturque in directum linea GP, ad oppositum punctum Q, in portione circuli OI. Dico factum esse quod oportuit. Hoc est, lineas GN et GQ, duas esse medias proportionales duabus GP et GI. Duas autem GP et GI, aequales esse duabus datis AB et CD. Atque adeo GN et GQ, duas esse medias inuentas proportionales duabus datis AB et CD.

1) Il résulte d'une lettre de Is. de la Peyrere, datée du 10 avril 1665, qu'il avait envoyé ses ‘folies’ à Chr. Huygens lorsque celui-ci se trouvait à Paris.

[p. 469]

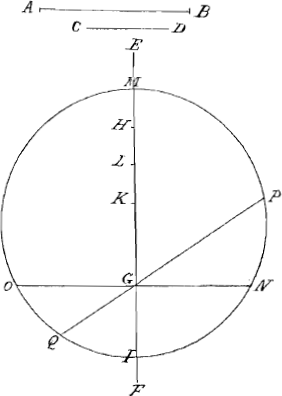
Constat enim primò ex constructione, lineas tres GM, GP et GN, esse continue proportionales. Rectangulum autem GP, GQ, aequale est quadrato GN, per 35 tertij²⁾. Erit ergo GN media proportionalis duabus GP et GQ, per 17 sexti. Ac proinde, quatuor lineae, GM, GP, GN, GQ erunt continue proportionales. Jam vero, rectangulum GM, GI, aequale est rectangulo GP, GQ, per eandem 35 tertij. Habebuntque rectangula illa duo aequalia, latera circum angulos aequales reciproca, per 14 sexti. Erit ergo vt GM ad GQ ita GP ad GI, Et alternando, erit GM ad GP, vt GQ ad GI. Sed vt GM ad GP, ita GN ad GQ, (demonstratum enim est quatuor esse continue proportionales). Erit ergo GQ ad GI, vt GN ad GQ, per 11 quinti. Et quinque lineae GM, GP, GN, GQ et GI erunt continue proportionales. Duae autem GN et GQ, mediae erunt proportionales duabus GP et GI. Facta verò fuit GI, aequalis per constructionem minori datae CD. Probandum restat lineam GP, aequalem esse maiori datae AB: vt demonstretur easdem GN et GQ, duas esse medias inuentas proportionales duabus datis AB et CD.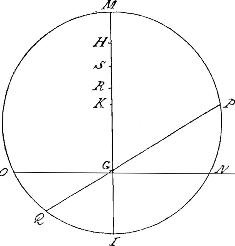

Quod vt fiat. Diuidatur differentia KM, quâ GM maior est GI, in duas partes SM et KS. Sitque SM, differentia rationis³⁾ GM ad GN. Et KS, differentia rationis GN ad GI. Auferatur ex SM, HM, vna ex tribus partibus aequalibus, in quas diuisa est per constructionem tota differentia KM. (Poterit autem auferri HM ex SM, quia SM maior est dimidiâ differentiae KM). Auferatur ex KS, RS, quae sit ad HM vt KS ad SM. Eritque residuum SH ad residuum KR, vt totum SM ad totum KS. Atque adeo quatuor partes HM, SH, RS, et KR, erunt proportionales.

Demonstratur esse continue proportionales. Constat enim, tres partes aequales HM, LH et KL, in quas diuisa est differentia KM, resolui in quatuor partes proportionales, HM, SH, RS et KR: Quarum quatuor partium, prima HM, facta est per constructionem aequalis HM, vna ex tribus illis partibus aequalibus differentiae KM. Duae igitur reliquae partes aequales LH et KL, eiusdem differentiae KM, resoluentur in tres reliquas par-

2) L'auteur se sert ici de la notation connue pour la proposition 35 du troisième livre des Eléments d'Euclide.

3) Ratio veut dire ici: différence.

[p. 470]

tes, SH, RS et KR. Quas dico esse proportionales. Eadem enim est ratio totarum trium partium HM, LH, et KL, ad quatuor totas partes HM, SH, RS et KR; quae ablatae HM, ad aequalem eius ablatam HM. Erunt igitur duae hae reliquae partes LH et KL, ad tres has reliquas partes SH, RS et KR; vt totae tres illae partes, ad totas illas quatuor partes. Et resoluentur duae hae reliquae partes, in tres has reliquas partes, eâdem ratione, quâ tres illae partes resoluuntur in quatuor illas partes. Sed tres illae partes resoluuntur proportionaliter, per quatuor illas partes; quae demonstratae sunt proportionales. Ergo et duae hae reliquae partes resoluentur proportionaliter, per tres has reliquas partes; ratione eâdem proportionales. At, quâ ratione tres hae reliquae partes sunt proportionales; erit SH ad RS, vt RS ad KR. Sed demonstratum est HM esse ad SH, vt RS ad KR. Erit ergo HM ad SH, vt SH ad RS, per 11 quinti. Et quatuor lineae HM, SH, RS et KR, erunt continue proportionales. Habebunt itaque quatuor hae lineae eandem rationem ad totam differentiam KM, quam habent ad totam eandem, quatuor differentiae rationum quatuor harum similium, GM ad GP, GP ad GN, GN ad GQ, GQ ad GI. Quia enim KM, tota est differentia quatuor harum rationum similium. Et per 7 quinti, quatuor hae lineae, aequales erunt quatuor harum rationum differentiis. Jmo quatuor hae lineae, differentiae ipsissimae erunt quatuor harum rationum similium. Quod ex appositâ figurâ clarisime apparebit.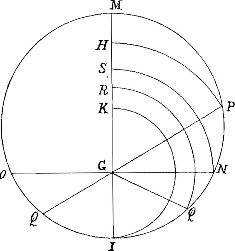

Erit ergo HM, differentia primae rationis GM ad GP. Nec non eadem HM, excessus erit, quo GM maior est GP. Sed eadem HM excessus etiam est, quo eadem GM maior est GH. Ablato ergo communi ambabus GH et GP, excessu HM: supererit GH aequalis GP. Atqui GH facta fuit aequalis per constructionem, maiori datae AB. Ergo et GP aequalis erit eidem maiori datae AB.

Demonstratis igitur duabus lineis GP et GI, aequalibus duabus datis AB et CD. Demonstratis itidem duabus GN et GQ, mediis proportionalibus duabus GP et GI. Demonstratum etiam erit, easdem GN et GQ, duas esse medias, inuentas proportionales duabus datis AB et CD, quod fuerat propositum.