Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 453.
Christiaan Huygens à J. Hudde.
24 janvier 1658.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 449.

Sommaire: Wanneer ontfangen. Van Archimedes. Excusatio laudis. Prima inventio praecipua nam et Heuraetius nunc. Aengaende het schryven is VE beter geluckt als gelooft.
De tangenten aengaende beloof ick daer op hier naer te sullen dencken en VE laten weten of gevonden heb of niet. doch ic meen dat wel vinden sal, door dien ic de maniere van Des Cartes constructien wel weet, en te meer om dat de cromme mij nu recht bekent is, wat het voor een is en de syne oock. fine methodo. Aengaende het centrum gravitatis van sijn eerste sien ick dat waer is 't geen ic gedacht hadde. maer was ons onmogelyck te raeden, om dat anders voorgestelt was, noch niet geseyt was doen wy geensins wisten dat het een stuc was van Slusij kromme. Maar nu wy weten dat het een cubica parabola is, soo konnen wij oock licht het centrum gravitatis van fGr in den diameter GS vinden, en dat op dese manier. datum hoc &c. Hier uyt siet VE oock hoe men de quadrature en centrum gravitatis van een stuc kan vinden.

Joh. Hudde.

Myn Heer

Voorleden Saterdagh¹⁾ braght mij de Heer Professor Schoten VE aengenaeme vanden 7^e deses, hebbende deselve 10 dagen by sich gehouden, het welck te langh

1) C'était le 19 janvier.

[p. 126]

waer indien wij nieuwe tydingen verhandelden. Het ghene VE voor af scrijft aengaende de 2 inventien van Archimedes ten opsight vande welcke VE hem boven alle de oude prefereert derf ick naeuwelyck geloven dat het soude slaen op myne inventie van de superficies van het Conoides parabolicum, alsoo ick wel weet dat die geensins van soo veel gewight en is. het is het geluck van de oude geweest dat voor haer alle de voornaemste theoremata noch ledigh stonden en te vinden waeren. onder welcke ick mede achte dat de metingh van de parabola en van de superficies van een bol van de uytnemenste syn.

Op de beleefde verantwoordinghe die VE wederom van nieuws voorwendt, sal ick alleen dit seggen dat indien VE deselve nodigh geacht heeft, ick dan mij even van het selfde als VE heb te beklaegen, te weten dat ick myn selven door myn schryvens niet genoegh en hebbe konnen uytbeelden, ende VE doen blycken hoe traegh ick ben om ergens uyt offensie te nemen, en hoe light om te vreden te stellen.

De constructie van de tangenten uyt een punt buyten de peripherie om dat ick sie dat VE daer op noch insisteert, beloof ick hier naer by gelegentheijdt te sullen soecken en VE bekent te maecken of ick die gevonden hebbe of niet. Het geene my doet gelooven dat ick daer wel sal toe geraecken is dat ick meermaels vele constructien uyt de vergelyckingh van twee aequatien hebbe gemaeckt. en daerenboven, dat ick nu gevonden hebbe dat VE eerste kromme als mede die van de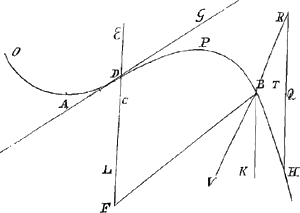



heer Sluse niet anders en is als een parabola cubica, het welck my wonder geeft ons soo lang onbekent is gebleven. Zij ADB de linie van Slusius; soo men nu neemt AC ∞ ⅓ van den diameter AB, ende ordinatim appliceert CD, soo is DPB en DAO elck een halve parabola cubica doch contrarie tegen malkander gestelt; FDF²⁾ beyder diameter, en de ordinatim applicatae, als BF, parallel met DG tangens in het punt D. VE. eerste kromme, BH, is dan mede een deel van dese parabola, waer door nu alles gegeven is het geen men soude mogen willen weten aengaende de quadrature centra gravitatis en solida van dese linien. Want getrocken sijnde HQ en BK parallel met DC en HKL met AB. soo kan men niet alleen

2) Lisez: FDE.

[p. 127]

weten het centrum gravitatis van het dubbele stuck BQH, dat is van RBH, waer mede VE sich nu voldaen houdt, maer oock het centrum gravitatis van het stuck HBK, ofte sijn dobbel HBV, het welck wij meynden te moeten vinden om dat ons eerst soo voorgegeven was en het contrarie van VE niet en hadden verstaen, selfs doen ghij ons de overeenkomst aenweest van Uwe en Slusij crommen. De quadraturen van dese stucken syn noch gereder te vinden als de centra gravitatis en dan voorts uijt beyde de groote van de solida door het omdrayen van dese figuren gemaeckt tot den inhoud van cylinders. Het welck alles ick wel wete, dat niet van node en is VE aen te wysen op wat manier moet ondersocht werden. Het centrum gravitatis van RBH vind ick den diameter BQ te deelen in T soo dat BT is tegen TQ als 15 y + 10 a + 6yy/a tot 5 y + 5 a + 3/2 yy/a. synde AB ∞ a en BQ ∞ y. doch dit door een ander middel die korter reeckeningh geeft.

Het is my leet te hooren dat VE door soo veel andere occupatien van de Geometrische studien wordt afgetrocken: het selfde geven my van haer de Heer Sluse en Monsieur Heuraet te kennen, dien ick beneffens VE geeren van den tydt die my overigh is soude bysetten, indien ick daer tegen van haere naerstigheijt geleertheydt en geest deelachtigh mochte werden. Ick blyve

Mijn Heer

VE dienstwilligen Dienaer Chr. Huygens van Zuylichem.

24 Jan. 1658.