Oeuvres complètes. Tome II. Correspondance 1657-1659
(1889)–Christiaan Huygens–No 419.
| |||||||||
[pagina 74]
| |||||||||
judicavit) tangentem, quam unicè per ocium mihi quaerere atque invenire datum fuit, cum tangentibus aliorum duorum consentire deprehendi; et quod ad ejusdem quadraturam ac gravitatis centrum attinet, deprehendi simul eos in eandem solutionem incidisse, quamvis diversis vijs illam quaesivisse mihi visi sint. Adeò ut minimè dubitare queam, quin omnia etiam inventis tuis sint responsura. 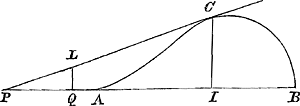 Quae igitur ad tangentem hujus curvae spectant, illa sic se habent. Suppositâ AB ∞ a QL ∞ b QA ∞ c PA ∞ d AI ∞ x et IC ∞ y: erit aequatio, exhibens quo pacto tangens PC sit ducenda, quando punctum C est datum, d ∞ 2xx - ax/2a - 3x. At si ipsa ex puncto P in producto axe prodire debeat, erit aequatio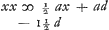 . Ac denique si ipsa ex L, puncto extra axem dato, sit ducenda, aequatio erit . Ac denique si ipsa ex L, puncto extra axem dato, sit ducenda, aequatio erit 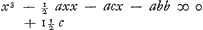 . Quae quidem construi potest, . Quae quidem construi potest,
utendo tantum rectis lineis et circulis.
Corollaria, [ex praece] dentibusGa naar voetnoot1) aequationibus resultantia.
| |||||||||
[pagina 75]
| |||||||||
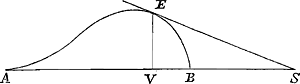 Suppositâ AB ∞ a BS ∞ d VB ∞ x et VE ∞ y: erit aequatio, exhibens quo pacto tangens SE duci possit, puncto E existente dato, d ∞ 2xx/a - 3x. Sed, quando punctum S datum est, aequatio erit xx + 1½ dx - ½ ad ∞ 0. Quod verò aequationem concernit, quâ tangentem hanc, è puncto, extra axem dato, ducere licet, ipsius quidem atque superioris par ratio est.
Hinc sequentia Corollaria emergunt.
Rel[iqua ad]Ga naar voetnoot2) quadraturam et gravitatis centrum hujus curvae spectantia, sunt hujusmodi. 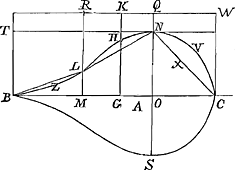 Fiat BG ∞ GC; BM ∞ MO ∞ OC; ducanturque perpendiculares MR, GK, et OQ, secantes curvam in L, H, et N. Deinde, assumptâ HK ∞ ⅓ HG, vel NQ ∞ ⅛ NO, vel LR ∞ 1 ¼ LM, erit ▭ BW ∞ datae figurae BZLHNVCSB. 2do. Ducendo NT parallelam BO, erit ▭ BN ∞ portioni BZL HNOSB, adeoque ▭ TQ + ▭ OW ∞ reliquae portioni NVCSN; et ▭ TK ∞ portioni NVCXN. 3tio. NOS erit maxima latitudo curvae; L punctum flexus; et portio BZL ∞ portioni LHN. 4to. Sumendo CA ∞ ⅖ BC, erit A centrum gravitatis datae figurae BZLHNVCSB. Quibus cum abundè quaesitis tuis satisfactum putent, rogarunt ut vicissim tibi, in | |||||||||
[pagina 76]
| |||||||||
gratiarum actionem, tangentes, quadraturas, atque gravitatis centra trium sequentium figurarum invenienda proponerem.
Esto AG diameter; FD semi-ordinata; AD ∞ x; DF ∞ y: sitque AG cognita et ∞ a. 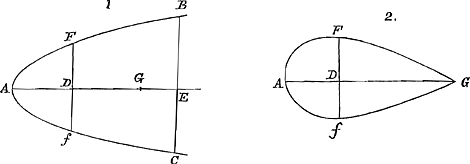 Proprietates.
1 mae figurae. aax ∞ y3 + 2ayy + aay. 2dae figurae. y6 ✱ - 3axy4 - 2aaxy3 + 3aaxxyy - 6a3xxy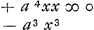 . .
3tiae figurae. x + y ∞ √√ ax3.
Quantum ad constructionem centri gravitatis atque quadraturae harum trium figurarum spectat, asserunt illam omnino facilem esse; et quantum ad inveniendas tangentes, modum easdem è vestigio investigandi extare in Cartesio. His vale ac me amare perge.
Lugd. Bat. 29 Octobris, 1657.
A Monsieur Monsieur, Christianus Hugenius, ten huijse van Mijn Heer van Zuijlechem. in S' Graven-hage. op t' pleijn. cito cito port. |
|


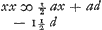 cum 2do Corollario sequitur ex puncto quolibet, in producto axe dato, unam duntaxat tangentem duci posse; sed ex puncto quocunque in axe usque ad extremum punctum, è quo tangentem ducere licet, duas semper diversas duci posse, quarum una concavam et altera convexam portionem contingat. Ubi simul liquet, à parte maximae latitudinis hujus curvae non praeter unum punctum flexus reperiri. Atque haec quidem, quae à sinistra
cum 2do Corollario sequitur ex puncto quolibet, in producto axe dato, unam duntaxat tangentem duci posse; sed ex puncto quocunque in axe usque ad extremum punctum, è quo tangentem ducere licet, duas semper diversas duci posse, quarum una concavam et altera convexam portionem contingat. Ubi simul liquet, à parte maximae latitudinis hujus curvae non praeter unum punctum flexus reperiri. Atque haec quidem, quae à sinistra