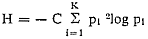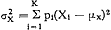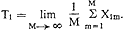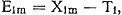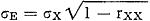Methodologie
(1961)–A.D. de Groot–
[pagina 279]
| |
8;3 Nauwkeurigheid en stabiliteit: meet-betrouwbaarheid8;3;1 Differentiatie van de meetschaal.De vraag naar de mate van nauwkeurigheid waarmee een instrument meet, laat zich vanuit verschillende gezichtspunten bezien. Een doorzichtige en moderne algemene definitie is de volgende: Een instrument meet des te nauwkeuriger, naarmate één meetuitkomst gemiddeld meer relevante informatie verstrekt met betrekking tot de waarde van de bijbehorende variabele. Daarbij moet dan nader worden bepaald, ten eerste, wat wij zullen verstaan onder (hoeveelheid) ‘informatie’, ten tweede, wat de toevoeging ‘relevant’ in dit verband betekent. Wij beperken ons voorlopig tot het eerste probleem en tot de empirische maatstaven die voor nauwkeurigheid-òngeacht-relevantie kunnen worden opgesteld. Dit is uitsluitend een kwestie van de gebruikte meetschaal en wel van de mate van differentiatie tussen meetuitkomsten, die de gebruikte schaal mogelijk maakt. Het zal duidelijk zijn, dat de gedifferentieerdheid van de schaal nauw samenhangt met wat wij onder nauwkeurigheid verstaan. Als men bijvoorbeeld in een gegeven materiaal van meetuitkomsten de differentiatie vermindert door klassen samen te vatten, bijvoorbeeld door in decimeters in plaats van centimeters te gaan meten of door een nominale indeling naar (b.v.) godsdienst in 5 klassen te reduceren tot een dichotomie (R.K. of niet-R.K.), dan ‘gaat er informatie verloren’;de meetschaal wordt grover, minder nauwkeurig. Een voor de hand liggende maatstaf voor de mate van differentiatie van de schaal is het aantal onderscheiden categorieën of klassen, K. Zoals bekend neemt men tegenwoordig gewoonlijk niet dit aantal zelf als maatstaf, maar de logarithme ervan voor het grondtal 2. Men definieert de variëteit V van de schaal aldus (variety, vgl. b.v. ashby 1957, p. 126): V = 2log K. Deze grootheid heeft in het geval dat K een macht van 2 is een zeer concrete, simpele betekenis, namelijk: het aantal vragen, dat men met ‘Ja’ of ‘Neen’ moet beantwoorden - in de terminologie van Shannon's informatie-theorie (shannon en weaver 1949): het aantal ‘binary digits’, of ‘bits’ - om de klasse, waarin een meetuitkomst ligt, te kunnen identificeren. Ingeval van acht genummerde klassen heeft men | |
[pagina 280]
| |
aan2log 8 = 3 vragen genoeg, bijvoorbeeld te beginnen met: ‘Behoort het element tot één van de eerste vier klassen?’, enz. Is behalve de schaal zelf ook de verdeling in het, oneindig gedachte, universum bekend, dan laat deze informatie-maatstaf zich verfijnen, namelijk door over te gaan op Shannon's entropie: waarin p1 de kans is, dat een element, volgens de universum verdeling, tot de i-de klasse behoort. Men kan gemakkelijk aantonen, dat in het bijzondere geval, dat de kansen voor alle klassen gelijk zijn (dus: p1 = 1/K voor alle i), H in V overgaat, wanneer wij de constante C = 1 stellen. Dit is tevens de voorwaarde voor de p1, waarvoor H maximaal wordt: afwijkingen van gelijkheid van kansen verminderen de entropie, dus de differentiatie of nauwkeurigheid van de schaal, volgens deze maatstaf. Dat deze vermindering reëel is laat zich gemakkelijk door een extreem voorbeeld aantonen. Stel dat b.v. p1 =0,9 is, zodat voor p2 t.m. pK nog maar 0,1 overblijft ( 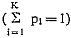 p1 = 1); dan zal in 9 van de 10 gevallen de uitkomst ‘oninteressant’ zijn. De gemiddelde hoeveelheid informatie, die één meetuitkomst verstrekt, is dus aanzienlijk geringer dan wanneer de kansen gelijkmatiger over de klassen verdeeld zijn; de differentiatie van de schaal is relatief gering. p1 = 1); dan zal in 9 van de 10 gevallen de uitkomst ‘oninteressant’ zijn. De gemiddelde hoeveelheid informatie, die één meetuitkomst verstrekt, is dus aanzienlijk geringer dan wanneer de kansen gelijkmatiger over de klassen verdeeld zijn; de differentiatie van de schaal is relatief gering.
Doordat voor de bepaling van de entropie, als informatie-theoretische differentiatie-maat, alleen gebruik wordt gemaakt van het aantal klassen en van de relatieve frequenties daarin, maakt het geen verschil of de schaal in kwestie een nominale, ordinale, interval- of verhoudingsschaal is. Bij de beide laatste (metrische) schaal-typen, waarbij men zinvol van ‘afstanden’ tussen schaalwaarden kan spreken, ligt het echter voor de hand hiervan bij de bepaling van de differentiatie gebruik te maken. Vandaar, dat men bij metrische schalen gewoonlijk werkt met differentiatieof spreidingsmaten, die gebaseerd zijn op het (universum-)gemiddelde, μx, en op de grootte van de afwijkingen daarvan. Zoals bekend wordt vaak met de variantie gewerkt: of met de wortel daaruit: σx, de standaard-afwijking. Deze differentiatie- | |
[pagina 281]
| |
maat berust op een andere gedachtengang: het afstands-begrip, het ‘uiteen-liggen’ van de X-waarden. De grootte-verhouding van H en σx is afhankelijk van de universumverdeling: zij meten niet hetzelfde.Ga naar voetnoot1 De variantie- of standaardafwijkingsmaat voor de differentiatie verdient in het algemeen de voorkeur als het afstands-begrip reële betekenis heeft en men de afstands-variatie wil verdisconteren. Een scherpe regel is hiervoor echter niet te geven. Blijkbaar is er zelfs voor de schijnbaar zo eenvoudige vraag naar de differentiatie - d.i. voor de meetnauwkeurigheid, ongeacht relevantie - niet één eenvoudige oplossing aan te bieden. Anders uitgedrukt: ook een begrip als ‘differentiatie van de schaal’, of ‘meetnauwkeurigheid (ongeacht relevantie)’ heeft klaarblijkelijk een surplus-betekenis ten opzichte van elk van zijn operationele definities. Dit zal eerst recht blijken als wij de restrictie ‘ongeacht relevantie’ laten vallen en naar de ‘nauwkeurigheid van een meting’ (8;3;2) of ‘van een meet-instrument’ (8;3;3) vragen. | |
8;3;2 Ware waarde en toevalsfout.In het algemeen kunnen wij niet aannemen, dat alle informatie, zoals die wordt verschaft door een meting in de schaal van het instrument, relevant is voor het metingsdoel. Wat met ‘relevant’ wordt bedoeld is misschien weer het beste duidelijk te maken door een score op of waarde van een variabele op te vatten als een door middel van het corresponderende instrument overgebracht bericht, van ‘zender’ naar ‘ontvanger’. De vraag, in hoeverre de verkregen informatie relevant is, correspondeert dan met de vraag, in hoeverre het ontvangen bericht overeenstemt met de ‘ware’, verzonden boodschap. In de informatie-theorie onderscheidt men tweeërlei foutenbronnen in de overbrenging: distorties en ruis (noise). Als er een systematische fout in de overbrengings-procedure besloten ligt, bijvoorbeeld in die zin dat er geen identiteit bestaat, maar wel een bepaald functioneel verband tussen verzonden en ontvangen signaal, dan spreekt men van ‘distortie’. | |
[pagina 282]
| |
Van ‘ruis’ spreken we als (we aannemen, dat) een dergelijke functionele afhankelijkheid niet bestaat: de fouten in de overbrenging zijn toevallige fouten. Uit de formulering blijkt reeds, dat de onderscheiding tussen distortie en ruis uit de informatie-theorie correspondeert met die tussen systematische en toevallige fouten in de statistiek. Wij zullen hier de distorties - ‘verdraaiingen’ zou een goede vernederlandsing zijn - buiten beschouwing laten. Zij berusten bij definitie op een systematische fout, die of in de ruimere experimentele opzet kan schuilen - om zo te zeggen buiten verantwoordelijkheid van het instrument in kwestie - of in gebreken in de (begrips-)validiteit van het instrument. Als er bijvoorbeeld aanleiding is, om aan te nemen dat de score op een vragenlijst, die bedoeld is om te meten hoe ‘autoritair’ de proefpersoon is (adorno e.a. 1950), mede wordt beïnvloed door de neiging om gedrukte uitspraken eerder te bevestigen dan te ontkennen (set to acquiescence, vgl. b.v. bass 1955), dan is dit een fout van het instrument, die afbreuk doet aan de realisering van het bedoelde begrip (autoritair); de schoen wringt bij de validiteit en niet bij de meet-nauwkeurigheid. Toevallige fouten, zoals die bijvoorbeeld kunnen ontstaan doordat de proefpersoon op een bepaald item ‘Ja’ antwoordt terwijl hij evengoed ‘Neen’ had kunnen antwoorden, of doordat hij zich bij het opschrijven of aanstrepen vergist, zijn daarentegen te beschouwen als ‘ruis’. Men kan ze opvatten als een effect van gebreken in de nauwkeurigheid (precisie) van het instrument. In termen van meting hebben wij hier te doen met de vraag in hoeverre de gevonden waarde van de variabele, in de gegeven schaal, door de invloed van toevallige fouten is vertekend ten opzichte van de ware waarde. De ‘ware waarde’, of in het quantitatieve (metrische) geval, de ‘ware score’, correspondeert met het verzonden bericht of signaal; de ‘gevonden waarde’ (of ‘score’) met het ontvangen bericht of signaal. Deze begrippen hebben een duidelijke zin in het geval van metings-, schattings- of benaderings-methoden (-instrumenten) met betrekking tot attributen van objecten, waarvan wij geen reden hebben om eraan te twijfelen, dat zij een ware waarde ‘hebben’; b.v.: afstanden, afmetingen, aantallen, tijdsduur- en hoeveelheidsmaten, of, om een nominaal voorbeeld te noemen: een te determineren species in de zoölogie. Anders uitgedrukt: de operationele definitie van de variabele zoals die in het instrument geïncorporeerd is, wordt gezien als een methode tot benadering | |
[pagina 283]
| |
van een ware waarde, die misschien nu niet in feite, maar wel in principe langs meer directe, meer precieze weg kan worden bepaald en die in ieder geval ‘bestaat’. Wat kan men doen om de invloed van toevallige fouten te bepalen en te bestrijden, in geval die meer precieze meetmethode niet toepasbaar is? Het antwoord is bekend uit de meting in de natuurkunde: men kan de invloed van toevallige fouten - niet die van systematische distorties - langs statistische weg verminderen door de meting van het object in kwestie een aantal keren te herhalen. Door herhaalde metingen kan men, ten eerste, tot op zekere hoogte de veronderstelling controleren, dat er sprake is van toevallige fouten. De verdeling van de meetuitkomsten moet het karakter hebben van toevallige afwijkingen rondom een centrale tendentie - die door de ware waarde wordt bepaald. Als er bijvoorbeeld in een intervalschaal sprake is van toevallige meetfouten, dan moeten de meetuitkomsten zich volgens een normale (Gauss-)verdeling rangschikken om de - onbekende - ware score. Weliswaar is de omgekeerde conclusie, van normaliteit van de verdeling naar toeval als ‘oorzaak’, niet altijd verantwoord; maar men heeft toch een controle. Neemt men vervolgens inderdaad aan dat de fouten toevalsfouten zijn, dan kan men, ten tweede, door de veelheid van metingen tot een betere benadering van de ware waarde geraken. In het geval van de intervalschaal is de meest adequate benadering, zoals bekend, het gemiddelde van de verkregen meetuitkomsten. De nauwkeurigheid van de benadering van de ware waarde laat zich opvoeren door het aantal herhalingen te vergroten en de meetuitkomsten te middelen. Wil men deze gedachtengang toepassen op meting in de sociale wetenschappen, dan doen zich enkele eigenaardige moeilijkheden voor. De eerste is deze, dat de ‘ware waarde’ niet alleen niet zonder het instrument in kwestie kan worden bepaald, maar ook niet goed onafhankelijk van het instrument kan worden gedefinieerd. Anders uitgedrukt: het ‘verzonden bericht’ is niet alleen slechts te benaderen met behulp van het bericht, dat via één bepaalde overbrengingswijze werd ontvangen, maar het is ook vaak gewrongen om aan te nemen, dat er een ‘waar’ verzonden bericht bestaat. Zo is het bijvoorbeeld weinig zinvol om aan een proefpersoon gedurende zijn testonderzoek - de stabiliteits-kwestie blijft hier buiten beschouwing (vgl. 8;3;4) - een ‘ware’ Wechsler-intelligentie toe te schrijven, die afwijkt van wat de test heeft opgeleverd. | |
[pagina 284]
| |
Aan de andere kant moeten wij echter wel aannemen, dat ook bij dergelijke metingen het eindresultaat, de gevonden waarde van de variabele, voor een deel door toevalligheden wordt bepaald. Wij schrijven dus toch, in een geval als dit (met een score in een intervalschaal): gevonden score = ‘ware score’ + fout-score. De vraag is nu echter, hoe deze ‘ware score’ moet worden gedefinieerd. De meest gebruikelijke oplossing is de ‘ware waarde’ op de variabele voor een gegeven meetobject in principe te definiëren via herhalingen van de meting. Beperken wij ons voor de uitwerking van deze gedachte weer tot de metrische schalen, dan is het duidelijk dat ook hier (vgl. p. 283), onder de aanname van uitsluitend toevallige fouten, het gemiddelde van de meetuitkomsten van een zo groot mogelijk aantal herhalingen de beste benadering is. De aanname ‘uitsluitend toevallige fouten’ is equivalent met de aanname, dat dit gemiddelde bij toename van het aantal herhalingen tot een limiet moet naderen, zodat wij kunnen stellen, dat de ‘ware score’ bij definitie de limiet van de gemiddelde score is. In formule, als X1ms de m-de meetuitkomst voor object i is: Is de ‘ware score’ eenmaal gedefinieerd, dan is de fout-score, E1m: en de mate van onbetrouwbaarheid of de standaardfout van de meting van object i is te definiëren als de standaardafwijking σE1 van de E1m- scores. Bij zwakkere schalen - nominaal, ordinaal - mag men niet middelen, zodat deze definitie-formule daarvoor niet bruikbaar is. Men kan echter ook daar, in principe, van de extra informatie, die herhaalde metingen met zich meebrengen, gebruik maken, ten eerste om te controleren of er sprake is van toevalsfouten, ten tweede om met meer zekerheid een ‘ware waarde’ te bepalen, respectievelijk te definiëren, en ten derde om een probabilistische maatstaf voor de onbetrouwbaarheid van één objectmeting op te stellen. De lezer zal zich intussen wel al hebben afgevraagd, hoe de, nog niet genoemde, tweede typische moeilijkheid voor metingen in de gedragswetenschappen moet worden opgelost, de moeilijkheid namelijk dat men de meting van object i in feite bijna nooit (M maal) kan herhalen. Het feit, dat men M niet werkelijk tot oneindig kan laten naderen is niet het | |
[pagina 285]
| |
grote probleem - daar zijn benaderingsmethoden (voor T1 en σE1) voor - maar: M komt dikwijls helemaal niet van de grond. Ten eerste zijn veel instrumenten erop gericht een toestand-nú te bepalen, bijvoorbeeld van een individu, een situatie, de publieke opinie. Wanneer men vorderingen in een leerproces, spanningen in een groep, of politieke gevoelens en attitudes wil meten, neemt men niet aan, dat dit stabiele kenmerken zijn. Herhalingen van de metingen zijn bij zulke gedragsvariabelen dus al onmogelijk omdat de te meten objecten in de tijd uit zichzelf veranderen. Ten tweede brengt de meting zelf vaak een onherstelbare verandering in de objecten (proefpersonen, respondenten, groepen) te weeg: zij ‘kennen de test’, zijn niet meer onbevangen, zien het nu anders of hebben het nu te gemakkelijk. Tengevolge van deze moeilijkheden zijn empirische benaderingen van T1 en van σE1 volgens de formules hierboven slechts hoogst zelden mogelijk. Vaak kan men de meting met een instrument hooguit één maal herhalen (M = 2); soms is ook dat onmogelijk. Men kan echter niettemin via de bovenstaande gedachtengang tot praktisch uitvoerbare bepalingen van de meetbetrouwbaarheid van instrumenten komen - zoals in de volgende paragraaf zal blijken. | |
8;3;3 Maten voor de meetbetrouwbaarheid van een instrument.In 8;3;1 hebben wij gesteld, dat een instrument des te nauwkeuriger meet, ‘naarmate één meetuitkomst gemiddeld meer relevante informatie verstrekt met betrekking tot de waarde van de bijbehorende variabele’. Verder hebben wij in die paragraaf onder het informatie-gezichtspunt de mate van differentiatie van de gebruikte schaal kort bestudeerd - ongeacht de ‘relevantie’ daarvan. In 8;3;2 is duidelijk geworden, voor het geval van één meet-object, wat in het verband van dit hoofdstuk onder ‘relevantie’ van informatie moet worden verstaan. Het gaat hier uitdrukkelijk niet om de betekenis van de variabele, maar om de afsplitsing van door toevalsfluctuaties veroorzaakte schijn-informatie. Het feit, dat deze afsplitsing in de gedragswetenschappen met betrekking tot één meet-object slechts zelden uitvoerbaar bleek te zijn, behoeft ons niet te verontrusten; wij zoeken immers naar een maatstaf voor de meetbetrouwbaarheid van het instrument, d.w.z. naar de betrouwbaarheid (relevantie) van meetuitkomsten met dit instrument, ‘gemiddeld’ (zie de definitie boven) over alle mogelijke objecten in het universum. Laten wij eerst aannemen, dat M = 2 mogelijk is. We veronderstellen | |
[pagina 286]
| |
dus, dat de metingsprocedure zich éénmaal laat herhalen, zonder dat de objecten intussen uit zichzelf veranderd of (nog) door de eerste meting beïnvloed zijn. In de praktijk van het onderzoek kan zich dit bijvoorbeeld voordoen bij een keuze-test of -vragenlijst, die erop gericht is via een groot aantal snel te beantwoorden vragen een (metrische) attitude- of belangstellings-variabele te bepalen. Als het aantal vragen groot genoeg en de beantwoording snel genoeg is geweest, is er vaak wel aanleiding om aan te nemen, dat de proefpersoon bij een hertest, na bijvoorbeeld een week of een maand, niets of zeer weinig meer weet van wat hij precies de eerste keer heeft gedaan, zodat de tweede beantwoording opnieuw onbevangen kan en zelfs moet zijn. Zijn er bovendien goede redenen om aan te nemen, dat de attitude of belangstelling in kwestie bij de proefpersonen zich over de relatief korte periode tussen test en hertest niet heeft gewijzigd, dan kan men volgens een geschikte methode de correlatie tussen twee reeksen uitkomsten van N proefpersonen berekenen; d.w.z. tussen Xi1 en Xi2 (i=l,2,... N). Deze correlatie-coëfficiënt, de meetbetrouwbaarheidscoëfficiënt, levert dan onder de genoemde veronderstellingen - géén Verandering van de gemeten objecten - een maatstaf op voor het relatieve effect van toevalsfluctuaties, over alle N proefpersonen gemiddeld; in dier voege dat de coëfficiënt groter zal zijn (dichter bij + 1 zal liggen) naarmate die invloed in het algemeen geringer is. Men kan de meetbetrouwbaarheidscoëfficiënt van het instrument, onder de genoemde veronderstellingen, definiëren als de grootte van deze correlatie in het betreffende universum, waaruit de N proefpersonen een steekproef vormen. De gevonden steekproef-correlatie is een schatting van de universum-correlatie. Het behoeft nauwelijks betoog, dat de betrouwbaarheid van deze schatting, evenals dit bij validiteits-coëfficiënten het geval is, afhangt, ten eerste van de representativiteit van de steekproef, ten tweede van zijn grootte (N). Ook hier kunnen zich bij de berekening complicaties voordoen, die correcties wenselijk maken; evenals dit het geval is bij (predictieve) validiteitscoëfficiënten (vgl. 8;2;1, p. 265). De meetbetrouwbaarheidscoëfficiënt laat zich op verschillende manieren verder interpreteren (vgl. b.v. gulliksen 1950, hfdst. 3). De belangrijkste afgeleide grootheid - opnieuw, voor een intervalschaal - is de zogenaamde standaardmeetfout van het instrument of van de variabele in kwestie. Onder zekere aannamen, met name de (aanvechtbare) aanname, dat de foutscores, Eim, voor verschillende meetobjecten (i) niet systematisch | |
[pagina 287]
| |
afhankelijk zijn van de grootte van de ware scores, Ti, kan men de limiet van de stand aard afwijking van de (normale) verdeling der Eim-waarden berekenen als het aantal meetobjecten, N, tot oneindig nadert. Deze standaardmeetfout, σE, blijkt dan gelijk te zijn aan: als σx = de standaardafwijking van de Xi1 (in het universum), voor i = 1, 2, 3,... N, en rxx = de betrouwbaarheidscoëfficiënt (in het universum) is. Deze formule is bijzonder bruikbaar en verhelderend. Terwijl het uit een oogpunt van differentiatie van de (interval-)schaal op de grootte van σx aankomt, zoals we in 8;3;1 hebben gezien, gaat het uit het oogpunt van meetbetrouwbaarheid om de verhouding tussen σE en σx, en deze is σE/σx =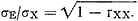 Hoe kleiner, relatief, dit getal is, des te hoger is de betrouwbaarheid van het instrument. Men kan door σx en rxx te schatten uit een steekproef tot concrete uitspraken komen over de mate van onbetrouwbaarheid van een met het instrument in kwestie gevonden score. σE wordt daarom ook wel de ‘standaard-meetfout van een gevonden score’ genoemd. Hoe kleiner, relatief, dit getal is, des te hoger is de betrouwbaarheid van het instrument. Men kan door σx en rxx te schatten uit een steekproef tot concrete uitspraken komen over de mate van onbetrouwbaarheid van een met het instrument in kwestie gevonden score. σE wordt daarom ook wel de ‘standaard-meetfout van een gevonden score’ genoemd.
Voor zwakkere schalen (niet-interval-schalen), waarvoor de hier geschetste gedachtengang uiteraard weer niet geldt, kunnen min of meer analoge methoden worden toegepast, die hier echter niet zullen worden besproken.
Tot zover werd de theorie van de meetbetrouwbaarheid gebaseerd op de veronderstelling, dat rxx in een steekproef kan worden bepaald, d.i. op de veronderstelling dat M =2 is, dus dat één herhaling van de meting, zonder verandering van de (N) meetobjecten, mogelijk is. De volgende vraag is, wat men moet doen, als ook deze veronderstelling niet vervuld kan worden geacht. Zoals we reeds hebben gezien (8;3;2) is dit vooral voor gedragsvariabelen, en met name voor test- en vragenlijst-variabelen een klemmende vraag. De herhaal-methode - in de testpsychologie gewoonlijk testhertest-methode genoemd - is bij zulke variabelen vaak niet toepasbaar. Werkt men met een kort tijds-interval tussen beide metingen dan is het geheugen-effect storend; werkt men met een lang tijds-interval dan kan men niet meer aannemen, dat de meetobjecten dezelfde zijn gebleven. | |
[pagina 288]
| |
Het laatste zou geen bezwaar zijn, als men mocht veronderstellen, dat alle meetobjecten op dezelfde wijze zouden zijn veranderd (preciezer uitgedrukt: volgens eenzelfde lineaire transformatie); maar ook deze veronderstelling is gewoonlijk onaanvaardbaar. Klaarblijkelijk moet nu ook de betrouwbaarheidscoëfficiënt, rxx, op een meer ingewikkelde manier worden geschat. In de psychometrie zijn hiervoor verschillende methoden ontwikkeld. Men kan, ten eerste, in plaats van een herhaalde meting met hetzelfde instrument, achtereenvolgens twee metingen verrichten (aan de N objecten) met twee parallelinstrumenten. Parallelinstrumenten zijn instrumenten, die géén vragen (items) gemeen hebben - zodat een onmiddellijk geheugen-effect uitgesloten is - maar waarvan (1) de (begrips-)validiteiten als gelijk kunnen worden beschouwd en (2) de verdelingen van waarden (c.q. scores) in het universum als gelijk kunnen worden beschouwd, of door een acceptabele transformatie gelijk kunnen worden gemaakt. De correlatie tussen de waarden verkregen bij metingen met twee zulke instrumenten wordt dan als schatting van rxx gebruikt. Men kan, ten tweede - als zelfs een dergelijke quasi-herhaling van de totale meting niet uitvoerbaar of ongewenst is - van een instrument, dat uit onderdelen (items) bestaat, twee ‘halve’ parallel-instrumenten maken. De verzameling items of onderdelen wordt dan in twee delen gesplitst, zodanig dat de beide helften zo goed mogelijk aan de inhoudelijke en statistische eisen voor parallel-instrumenten voldoen. Men correleert vervolgens de waarden (c.q. scores) der meet-objecten op deze beide ‘gehalveerde’ instrumenten en schat de grootte van de correlatie-coëfficiënt, die men zou hebben gekregen, als de twee helften de normale, dus dubbele lengte zouden hebben gehad. Een zo verkregen betrouwbaarheidsschatting wordt gewoonlijk de ‘split-halves-reliability’ (halveerbetrouwbaarheidscoëfficiënt) genoemd. Een derde methode, afkomstig van Kuder en Richardson, is gebaseerd op de, via de voorgaande stap begrijpelijke bevinding, dat de grootte van de betrouwbaarheid van een uit items bestaand instrument in belangrijke mate afhangt van de sterkte van de intercorrelaties van de items. Deze auteurs stellen zelfs (kuder en richardson 1937, p. 159): ‘Reliability is the characteristic of a test possessed by virtue of the positive intercorrelations of the items composing it.’ De door hen afgeleide en door vele anderen (o.a. jackson en ferguson 1941; tryon 1957) nader | |
[pagina 289]
| |
bewerkte formules leveren een voor bepaalde typen van instrumenten zeer bruikbare ondergrens-schatting voor rxx, die op een berekening of schatting van de item-intercorrelaties berust. De beide laatstgenoemde methoden hebben gemeen, dat gebruik wordt gemaakt van het feit, dat in instrumenten, die uit items bestaan, een zekere mate van interne quasi-herhaling pleegt op te treden. Anders uitgedrukt: men komt tot betrouwbaarheidsschattingen via bepalingen van de interne consistentie van het instrument, d.w.z. van de mate waarin de onderdelen elkaar ondersteunen (vgl. 8;4). De uiterste consequentie van deze gedachtengang is, dat men ieder item als een meetinstrument opvat en de totaalscore als het gemiddelde van de K item-scores. Men neemt dan aan, dat alle items, wat hun relevante aandeel betreft, hetzelfde meten - ze zijn immers positief gecorreleerd - zodat men in feite te doen heeft met K herhalingen (replicaties) van de meet-procedure (vgl. 8;3;2). Gaat men zo te werk, dan kunnen variantie-analytische methoden worden toegepast voor de afleiding van betrouwbaarheidsformules. Mutatis mutandis kunnen weer soortgelijke bewerkingen worden uitgevoerd met instrumenten, die niet in een intervalschaal, maar in een nominale of ordinale schaal meten. Wij moeten hier echter met deze constatering volstaan. Voor formules, theoretische uitwerkingen en andere benaderingen van de betrouwbaarheidsgedachte en voor technische details zij verwezen naar de op dit gebied bijzonder uitgebreide literatuur (wiegersma 1960a; ferguson 1947; gulliksen 1950; loevinger 1957; hoyt 1951; lord 1955 en 1959; rajaratnam 1960, e.a.). | |
8;3;4 Het stabiliteitsprobleem.Bij elk van de hierboven genoemde methoden om tot een schatting van de universum-betrouwbaarheid te komen behoren bepaalde empirische condities. Bij bepaling van de herhalings-betrouwbaarheid van een instrument wordt bijvoorbeeld aangenomen, dat de meetobjecten niet intussen veranderd zijn; bij de parallel-betrouwbaarheid wordt verondersteld, dat de twee instrumenten exacte parallel-instrumenten zijn; bij de op interne consistentie gebaseerde schattingen van de betrouwbaarheid moeten de items aan bepaalde condities voldoen. Als al deze condities exact vervuld waren, dan zouden praktisch alle betrouwbaarheidsbepalingen op hetzelfde neerkomen. De theoretische basis is in principe steeds dezelfde: men stelt Xim = Ti + Eim, neemt aan dat de gemiddelde foutscore Eim | |
[pagina 290]
| |
in het universum gelijk 0 is en dat Eim niet met Ti gecorreleerd is.Ga naar voetnoot1 De verschillen tussen de diverse methoden liggen niet zozeer in de uitgangspunten, als wel in hun uitwerking. Deze uitwerking sluit aan op verschillende secundaire veronderstellingen over empirische condities - die in werkelijkheid nooit exact vervuld zijn. Dit betekent, dat de verschillende betrouwbaarheidsformules in de praktijk verschillende betekenis hebben: zij evalueren de invloed van verschillende soorten toevallige fouten. Uit een praktisch oogpunt is, zeker voor gedragsvariabelen, verreweg de belangrijkste onderscheiding tussen de verschillende methoden die naar de aan- of afwezigheid van een tijdsinterval tussen verschillende metingen. Bij methoden als Kuder-Richardson en de halveer-coëfficiënt worden in het algemeen alle benodigde gegevens in één zitting opgenomen. Weliswaar heeft deze zitting een zekere duur, zodat wij dus de mogelijkheid van een leerproces, of van vermoeidheids- of verzadigings-verschijnselen niet geheel kunnen uitsluiten, maar toch is het meestal wel redelijk om aan te nemen, dat het te meten attribuut tijdens deze zitting niet zodanig is veranderd, dat de betrouwbaarheidscoëfficiënt daardoor is beïnvloed. Nemen wij dit aan, dan is wat wij in rxx meten de (meet-)betrouwbaarheid van het instrument. Bij toepassing van de parallelmethode en zeker bij de herhalings-methode is er echter noodzakelijkerwijze een interval, waarin de te meten grootheid zèlf kan veranderen. Wat de twee soorten verandering betreft - onder invloed van de meting zelf (‘geheugen-effect’), of van ‘spontane instabiliteit’ van de variabele (vgl. 8;3;3) - is het duidelijk, dat wij de eerste eigenlijk liefst zouden willen uitschakelen. Wat de tweede betreft is dit echter minder duidelijk. Het komt voor, dat men een variabele wil meten, waarvan men aanneemt, dat deze voor een bepaald object (individu) een vaste waarde heeft gedurende een zekere tijd, ondanks het feit, dat de meetuitkomst ook binnen die tijd fluctuaties te zien geeft die niet aan het instrument maar aan de ‘onbetrouwbaarheid’ van het object liggen. Die fluctuaties worden dan als onbelangrijk beschouwd: men ziet ze als een gevolg van het feit, | |
[pagina 291]
| |
dat wij, met onze methode, nu eenmaal niet in staat zijn de ‘ware’, constante waarde te vinden. Stel, dat men de lengte van objecten (b.v. staven) moet bepalen onder omstandigheden, waarin het niet mogelijk is de temperatuur onder controle te houden, noch deze te bepalen. Wij weten, dat temperatuursverschillen fluctuaties veroorzaken, maar omdat er geen middelen zijn om de temperatuur te bepalen, kunnen wij die fluctuaties niet experimenteel uitschakelen. Onder zulke omstandigheden zal men nu allicht in maatstaven voor de onbetrouwbaarheid van de metingsprocedure de onzekerheid ten gevolge van ‘toevallige’ temperatuur-fluctuatie inbegrijpen. In de gedragswetenschappen komen zulke situaties zeer vaak voor. Men wil bijvoorbeeld een persoonlijkheidsvariabele (zeg, de ‘introversie’ van proefpersonen) bepalen, door middel van een vragenlijst. Dat de introversie-score van een proefpersoon mede wordt beïnvloed door zijn stemming, zijn conditie, recente ervaringen, etc., lijdt geen twijfel; maar in deze oncontroleerbare en/of onbelangrijke afwijkingen zijn wij niet geinteresseerd. Het gaat om de ‘mate van introversie’ die de proefpersoon, in zijn tegenwoordige ontwikkelingsstadium, geacht wordt te ‘hebben’. Hoe ‘betrouwbaar’ kunnen wij deze meten? Het is duidelijk, dat in zulke gevallen, waarin wij in onze ‘meting’ van zekere fluctuaties van het object zelf willen abstraheren, een betrouwbaarheids-bepaling mèt interval zinvoller is dan één zonder. Wanneer wij, in het algemeen, met een betrouwbaarheids-maatstaf, niet alleen de precisie van het instrument maar ook, in deze zin, de graad van stabiliteit van het object willen dekken, zijn methoden als de parallel-betrouwbaarheid en met name die van de test-hertest-betrouwbaarheid adequaat. Men doet er dan zelfs goed aan ervoor zorg te dragen, dat het interval tussen de twee series metingen niet te klein is: dat vermindert het geheugen-effect en versterkt de kans op die ‘toevallige’ object-fluctuaties, waarvan wij de storende invloed willen leren kennen - in de hoop dat zij niet te groot zullen zijn. Het is duidelijk, dat wij hier de invloed van een ander soort ‘toevallige fouten’ evalueren. Wij hebben niet meer te doen met de meet-betrouwbaarheid van het instrument - die beter door middel van Kuder-Richardson of de halveer-methode kan worden geschat - maar van een achtergrondsvariabele, waarvan de verkregen variabele een benadering is. | |
[pagina 292]
| |
Het feit, dat nu ook de object-fluctuaties als toevals-fluctuaties worden beschouwd, maakt dat men ook hier nog wel kan volhouden, dat het instrument en de variabele geheel met elkaar corresponderen, d.i. dat het instrument de variabele definieert. Traditioneel wordt in ieder geval ook deze vorm van rxx-bepaling, dus inclusief stabiliteits-evaluatie, onder het hoofdstuk (meet-)betrouwbaarheid (reliability) behandeld. Men kan echter ook zeggen, dat men een andere variabele bedoelt dan men verkrijgt; zo beschouwd is het een kwestie van begrips-validiteit. Dit is echter slechts een kwestie van indeling (vgl. 8;2;5). Van belang is alleen, dat de verschillende betrouwbaarheids-begrippen goed onderscheiden worden. | |
8;3;5 Betekenis en gebruik van betrouwbaarheidsmaten.Is betrouwbaarheids-bepaling nuttig en nodig? Deze vraag wordt telkens weer gesteld - en meestal positief beantwoord. Er zijn weliswaar gevallen, waarin de validiteits-bevindingen met betrekking tot een variabele een zo duidelijke taal spreken, dat onze belangstelling voor de meetbetrouwbaarheid daarbij vergeleken in het niet verzinkt. Hoe meer een meet-instrument een gevestigde reputatie krijgt, hoe verder uitgewerkt en bevestigd het nomologisch net is, waarin de bijbehorende variabele en het bijbehorende begrip hun plaats hebben, des te minder belangrijk wordt het betrouwbaarheids-gezichtspunt. Maar dit is meer een kwestie van verminderde. actualiteit van een reeds geïncorporeerd principe in de verder gevorderde stadia van meet-technologie, dan dat er een aanwijzing in te zien zou zijn voor de overbodigheid van de betrouwbaarheids-gedachte. Met andere woorden: de boven gestelde vraag kan, behalve natuurlijk bij een volstrekte leek, alleen opkomen bij een doorgewinterde (psycho-)metricus. Het is vooral in het constructie-stadium, bij nieuwe instrumentele realisering van begrippen, dat behalve aan de objectiviteit (hfdst. 6), aan de meet-nauwkeurigheid en -betrouwbaarheid van de te verkrijgen variabele aandacht moet worden besteed. Dit geldt allerminst alleen in de test-psychologie, waarin het begrip en de technologie vooral ontwikkeld zijn. Het betrouwbaarheids-gezichtspunt is van minstens even grote betekenis op gebieden, waarop het niet zo gemakkelijk en acceptabel te operationaliseren is als in de testpsychologie. De strekking van de betrouwbaarheidsgedachte is eenvoudig en algemeen toepasselijk: het | |
[pagina 293]
| |
gaat erom bij metingen en beoordelingen (vgl. 7;3) de invloed van als toevallig of niet-essentieel te beschouwen factoren - geluk, pech, invloed van gebrek aan precisie van het instrument, de invloed van de (toevallige) beoordelaar ook (7;3) - te reduceren en onder controle te houden en een onverantwoord afgaan op uitkomsten tegen te gaan. Dit is op de meest uiteenlopende gebieden van onderzoek en toepassing een belang van de eerste orde, dat echter maar al te vaak wordt verwaarloosd. Men neme bijvoorbeeld de onderwijspraktijk: het betrouwbaarheids-gezichtspunt schittert door een bijna volstrekte afwezigheid. Het feit, dat objectieve prestatie-maatstaven (type: vorderingentests) vrijwel ontbreken, betekent dat praktisch alleen wordt gewerkt met proefwerken en examenopgaven - b.v. van drie sommenGa naar voetnoot1 (die soms nog fout zijn); om maar te zwijgen van nog veel dubieuzer mondelinge beurten, en -examenprocedures (vgl. de groot 1959b). Deze methoden voldoen stellig niet aan de meest primitieve eisen van betrouwbaarheid. Natuurlijk kan men de grove onderscheidingen met dit systeem ook nog wel maken, terwijl de mogelijkheid van herhaalde toetsingen ongetwijfeld veel kan compenseren. Dit neemt echter niet weg, dat zwaarwegende beslissingen over grensgevallen maar al te vaak moeten worden gemaakt op een basis van onnodig onbetrouwbare gegevens. De Nederlandse onderwijspraktijk kan op dit punt zonder twijfel aanzienlijk worden verbeterd door een passende invoering van aan de test-theorie ontleende principes. Een ander gebied is, bijvoorbeeld, dat van de medische diagnostiek. Het betrouwbaarheids-gezichtspunt is hier niet afwezig; iedere patiënt en iedere medicus weet immers dat de laatste zich kan vergissen. Kwantitatieve, differentiële studies, die toch niet moeilijk zouden zijn uit te voeren, zijn echter schaars. In het algemeen kan men voor iedere variabele, iedere methode van onderscheiding, ieder ‘instrument’ - in onze, ruime betekenis - de betrouwbaarheidsvraag stellen en empirisch onderzoeken. Gaat het om procedures die een beoordeling vragen, dan moet het betrouwbaarheidsgezichtspunt met dat van de intersubjectiviteit (7;3) worden uitgebreid. Maar dat is, bij praktisch of theoretisch fundamentele | |
[pagina 294]
| |
onderscheidingsmethoden (dus: instrumenten) dan ook het minste, wat men kan doen. Vooral daar waar beslissingen met betrekking tot individuele gevallen op gebruik van een ‘instrument’ gebaseerd zijn - in de klinische psychologie, de medische praktijk, in de jurisdictie, het onderwijs, en op allerlei plaatsen in de ‘individualiserende’ cultuurwetenschappen (vgl. 9;4) - verdienen het betrouwbaarheidsgezichtspunt en de daarbij behorende eenvoudige controlemiddelen veel meer aandacht dan zij krijgen.
Uit het voorgaande zal duidelijk zijn geworden, dat de betekenis en het gebruik van betrouwbaarheidsmaatstaven afhankelijk zijn van de doelstelling, die de onderzoeker met de instrumentele realisering of met het gebruik van het instrument voor ogen heeft. Wij hebben reeds gesteld - en dit komt op hetzelfde neer - dat het betrouwbaarheidsgezichtspunt secundair is ten opzichte van de (begrips-)validiteit. De hantering ervan is afhankelijk van het begrip-zoals-bedoeld, in een gegeven onderzoek-context. Dit geldt ten eerste voor de keuze van een passende betrouwbaarheidsmaat. Het accent kan liggen op de precisie (differentiatie) van de schaal (8;3;1), op de nauwkeurigheid van de meting, in een gegeven schaal, van object i (8;3;2), op de betrouwbaarheid van een instrument (8;3;3), op de betrouwbaarheid inclusief stabiliteit van een variabele (8;3;4). Voor gedragsvariabelen is de keuze tussen de beide laatstgenoemde vormen dikwijls van belang. De vraag is dan of men met een maat op simultane of op successieve basis (met tijds-interval, 8;3;4) wil werken. Van beslissende betekenis daarbij is de mate waarin ‘essentiële’, d.i. niet als toevallig beschouwde veranderlijkheid, respectievelijk invariantie van een variabele over een zeker tijdsinterval wordt aangenomen. Dit ligt verschillend bij verschillende typen attributen (van een persoon, een groep, een situatie) en bij verschillende typen onderzoek. Men kan zich een reeks denken van ‘diepere’, als invariant beschouwde, naar meer ephemere, veranderlijke kenmerken; bijvoorbeeld voor een volwassen subject: persoonlijkheids-kenmerken - prestatie-variabelen (‘vermogens’) - fundamentele (centrale) attitudes - meer perifere attitudes en meningen - verworven vaardigheden en kennis (achievement) - stemmingen en gevoelens. Bij de laatste zou een bepaling van de betrouwbaarheid van de variabele met een tijdsinterval zinloos zijn, aangezien zulke instrumenten | |
[pagina 295]
| |
juist bedoeld zijn om de psychische toestand van het subject hier en nu te bepalen. Ligt het in de bedoeling een instrument te gebruiken voor onderzoek van een individuele persoon, groep of situatie, dan is dikwijls dat, wat men eigenlijk zou willen kennen, niet de meetbetrouwbaarheid van instrument of variabele in het algemeen - gemiddeld over alle objecten en schaal-waarden - maar de nauwkeurigheid van het meetresultaat bij dit ene object (i). Door de keuze van een passende betrouwbaarheids-maatstaf is het soms mogelijk ook hierop empirisch vat te krijgen, zij het alleen bij sommige instrumenten, die er door een ingebouwde (quasi-) herhaling op ingericht zijn. Ten tweede hangen ook de eisen, de normen voor een acceptabele nauwkeurigheid en meet-betrouwbaarheid, bij een eenmaal gekozen maat, sterk af van het onderzoek-doel. Voor psychometrische tests is bijvoorbeeld een gangbare conventie, dat rxx ≧ .90 behoort te zijn. Dit correspondeert met een waarde van σE/σX van ongeveer 0,3 - zodat bijvoorbeeld voor een intelligentie-quotient met μ = 100 en σx = 15 de standaardmeetfout σE = 4,5 wordt. Deze norm is echter niet meer dan een redelijke conventie: als basis voor individuele uitspraken of decisies is vaak een hogere betrouwbaarheid tenminste gewenst, terwijl men, ingeval het om de bepaling van groepsgemiddelden of bijvoorbeeld om grove (selectie-) onderscheidingen gaat, met een veel lagere betrouwbaarheid genoegen kan nemen. Geschiedt een interpretatie - bijvoorbeeld van klinische test-gegevens - uitsluitend in de zin van een vorming en/of selectie van hypothesen, die vervolgens met meer betrouwbare maatstaven zullen worden getoetst (cronbach en gleser 1957, p. 128 e.v.), dan behoeft de norm ook niet zo scherp te worden gesteld. Helaas worden echter in de praktijk, vooral van de klinische psychologie, nog maar al te vaak definitieve conclusies en decisies gebaseerd op onvoldoende betrouwbare gegevens. | |
8;3;6 Van meetuitkomst naar conclusie.Welke zijn de plaats en betekenis van betrouwbaarheidsoverwegingen, primo, in de generalisaties van het confirmatie-proces in een onderzoek en, secundo, in de interpretaties van het inferentie- en beslissingsproces bij een toepassing? Nemen wij eerst de (confirmatie-)gang van meetuitkomst naar begrip. | |
[pagina 296]
| |
De meetuitkomst, X1, is wat hier en nu werd gevonden, in een gegeven schaal, van een zekere precisie of differentiatie (8;3;1). Op basis van aannamen en bevindingen over de (gemiddelde) meetbetrouwbaarheid van het instrument (8;3;3) wordt aangenomen, dat de gevonden waarde de ware waarde voor object i, T1, behoorlijk, d.i. met een aanvaardbare mate van onnauwkeurigheid, representeert (8;3;2). De ‘ware waarde’ is dan de meest passende centrale tendentie-uitkomst (c.q. het gemiddelde), die gevonden zou zijn, indien de meting van object i onbeperkt zou kunnen worden herhaald, zónder verandering van het object. Vervolgens wordt, op basis van aannamen en bevindingen over de stabiliteit van de variabele met betrekking tot als toevallig beschouwde object-fluctuaties (meetbetrouwbaarheid in de zin van 8;3;4) deze ware waarde opgevat als een benadering, met een aanvaardbare mate van onnauwkeurigheid, van de invariant gedachte waarde van object i op de ‘kern’ van de variabele. Tenslotte wordt deze waarde, op basis van aannamen en bevindingen over de begripsvaliditeit van de (kern-)variabele, beschouwd als representant van object i's positie met betrekking tot het begrip-zoals-bedoeld. Stel bijvoorbeeld dat het instrument is: een eind-proefwerk voor meetkunde over de stof van de eerste klasse V.H. en M.O., waarmee de leraar het ‘verworven inzicht’ in dit vak wil toetsen (vgl. 6;2;3). Nemen wij gemakshalve aan, dat de beoordeling objectief kan geschieden, dan is het behaalde cijfer de meetuitkomst, in een bepaalde schaal met meer of minder differentiatie. De eerste aanname (meetbetrouwbaarheid van het instrument) houdt nu in, dat ‘geluk’ of ‘pech’ bij het vinden van de oplossing, bij het opschrijven, eventueel bij het afkijken, en bij de toepassing van de scorings-methode op dit geval, een voldoende bescheiden rol hebben gespeeld om het behaalde cijfer te kunnen opvatten als maatstaf voor wat de leerling vandaag kon presteren - met betrekking tot dit proefwerk. De tweede aanname (stabiliteit) heeft betrekking op de conditie en stemming van de leerling vandaag, met betrekking tot meetkunde: zou de uitslag gisteren, morgen, volgende week, wat die conditie betreft, dezelfde zijn geweest? Als hij vandaag hoofdpijn had is dat niet waarschijnlijk; maar een zekere stabiliteit over conditie-fluctuaties wordt aangenomen. De derde aanname (begripsvaliditeit) houdt in dat het een goed, geschikt proefwerk was, om ‘verworven begrip’ in meetkunde mee te bepalen, zodat men op grond van de uitslag kan zeggen, dat de | |
[pagina 297]
| |
leerling in kwestie een goed (voldoende, matig zwak) begrip van (eerste klasse-) meetkunde hééft. Gaan wij nu naar de toepassingssfeer over en veronderstellen wij bijvoorbeeld, dat van dit cijfer het rapportcijfer afhangt en daarvan de overgang van deze leerling. Er komt dan nog een vierde aanname bij, namelijk dat de gehanteerde beslissings-strategie adequaat is. Aan deze vierde aanname kan men een wat meer concrete vorm geven, door te veronderstellen, dat een ‘adequate strategie’ een strategie is, die in het algemeen goed voorspelt of een leerling het onderwijs in de volgende klas al dan niet ‘zal kunnen volgen’ (operationeel gedefinieerd). Ziet men de zaak zo, dan gaat het wat de rapportcijfers en dus ook wat het meetkunde-proefwerk-cijfer betreft, niet meer om begrips-validiteit, maar om predictieve validiteit: men wil er geen uitspraak over meetkundebegrip maar een voorspelling over toekomstig studie-succes op baseren. Bij deze opvatting overschaduwt het belang van deze predictieve validiteit (en van de keuze van een goede strategie) dat van de betrouwbaarheidsaannamen. Wij zien dus, opnieuw, dat bij voorspellend gebruik van een variabele betrouwbaarheidsoverwegingen van ondergeschikt belang zijn vergeleken bij de validiteit. De betrouwbaarheid is weliswaar niet geheel zonder invloed op de validiteit (de betrouwbaarheids-index (√rxx) in het universum markeert het maximum dat een validiteitscoëfficiënt theoretisch kan halen), maar afgezien van deze grensrelatie is de betrouwbaarheidsbepaling en -controle van ondergeschikt belang. Bij metend gebruik van een variabele daarentegen zijn de eerste twee generalisatiestappen altijd van grote betekenis. Het is vaak van belang ze afzonderlijk, met besef van die betekenis, te maken. |
|