|
| |
| |
| |
3. Appels en peren: wiskunde en psychologie
Met het optellen van appels en peren schijnt er volgens een bekend gezegde iets niet te kloppen. Het kan niet, of het mag niet, of het is onredelijk of onzedelijk, naar gelang de toevallige context van die beeldspraak. Bedoelen we het nu eens niet als beeldspraak maar echt, dan kan het heus. Immers:
twee appels en drie peren zijn samen vijf vruchten.
Wat echt niet kan, is niet het optellen maar het aftrekken:
twee appels van drie peren.
Probeer het maar!
Aan de andere kant is het volstrekt niet bezwaarlijk om
twee dubbeltjes bij drie kwartjes op te tellen
en ook
twee dubbeltjes van drie kwartjes af te trekken
of zelfs
twee stuiters bij drie bommen op te tellen
en
twee stuiters van drie bommen af te trekken.
Waar zit hem het verschil?
Het was maar een voorbeeld van een soort vragen die steeds weer aan de orde gesteld worden, hoewel ze al lang zijn beantwoord en dat op alle denkbare niveaus, samen met de vraag wat op welk niveau wenselijk en haalbaar is. Maar het is net als op school: je kunt iets nooit vaak genoeg zeggen.
Ik beperk me hier tot wat zich afspeelt rond de wiskunde-operaties van optellen en aftrekken. Vermenigvuldigen en delen waar het in principe eender mee gesteld is, laat ik voor het gemak buiten beschouwing.
Optellen heeft iets te maken met toevoegen en wegnemen. Dingmatig toevoegen en wegnemen. Ik zeg ‘dingmatig’ en niet ‘concreet’. De twee appels en drie peren kunnen concreet op een concrete schaal liggen, maar even fraai op een schaal liggend afgebeeld of verbeeld zijn en tenslotte hoeven het helemaal niet dé twee appels en dé drie peren te zijn, maar zo maar twee appels en zo maar drie peren: een algemeen tweetal appels en een algemeen drietal peren. Het zijn mijlenver uiteenliggende niveaus van abstracties waar behalve de piekerende filosoof niemand zich iets van aantrekt. Ik heb er, om er niet te veel soesa van te maken, het woord ‘dingmatig’ voor gekozen: dingmatig toevoegen en dingmatig weghalen. Van hoe concreet die ‘dingen’ zijn, hoef ik me niets aan te trekken. Optellen en aftrekken als rekenkundige bewerkingen in de realiteit gaat niet dingmatig maar getalmatig te werk (of volgens lengten, gewichten, geldwaarden, maar daar kom ik nog op terug). Of, anders gezegd, je moet goed uitkijken welke soort dingen je daar optelt en aftrekt.
Euclides zei: ‘Eenheid is datgene waarmee je elk ding één kunt noemen.’ Het klinkt vreemd, maar het wordt duidelijker als ik ermee doorga: ‘Tweeheid is datgene waarmee je elk tweetal dingen twee kunt noemen’, enzo-
| |
| |
voort. Zodoende kun je van twee paarden net zo praten als van bruine paarden, hoewel geen van die paarden twee is.
Euclides ging trouwens niet zo door, maar veeleer: Getal is de uit eenheden samengestelde verzameling. Dit was nog tot in deze eeuw het idee van wat getallen zijn: uit (denkbeeldige) eenheden samengesteld. Zelfs de onvolprezen Cantor huldigt nog deze opvatting, al laat hij oneindige verzamelingen toe. Om in de realiteit iets te tellen, op te tellen, af te trekken, grijp je als het ware naar dat denkbeeldige telraam van eenheden, je beeldt er de te tellen, de op te tellen, de af te trekken verzamelingen op af en voert de gewenste operaties op dit telraam uit. In de praktijk mag je dat denkbeeldige telraam best concretiseren of hoef je er niet eens een denkbeeldig of concreet telraam bij te halen. Je telt de mensen in de kamer door ze elk maar als mens te beschouwen (niet als Piet, Mies, man, vrouw, enzovoort) of hun neuzen (kleine, grote, kromme, rechte - het doet er niet toe). Je beschouwt wat je moet tellen als gelijksoortig; als je een soortnaam nodig hebt, verzin je er maar een (appels en peren zijn allebei vruchten). Je identificeert ze, berooft ze van alle kenmerken behalve van dat dat ze verschillen. Het zijn geen abstracte eenheden maar dingen, maar dan zonder speciale kenmerken. Zodoende kun je dan best twee appels bij drie peren op tellen, als je ze maar als vruchten signaleert, net zoals je de Jan, Piet, ... enzovoort in de kamer optelt door er mensen van te maken. Maar appels van peren aftrekken faalt al op het dingmatig niveau en het over één kam scheren komt er niet eens bij te pas.
Tegenwoordig houd je er achter dit concrete gebeuren een minder geïdealiseerde theorie op na. Het denkbeeldige telraam van eenheden hoeft niet. Je bent op de een of andere manier aan de getallenrij gekomen - in de praktijk door het opzeggen en op lange stroken schrijven van de telwoorden en cijfergetallen en in de mathematische theorie door wat je noemt de axioma's van Peano die je (onder meer) een 0 en bij elk getal één volgende garanderen. Dat zijn de dingen die je optelt en aftrekt en het verband met de realiteit wordt door afbeelden gelegd. Door een verzameling te tellen beeld je hem één-één in de telrij af tot hij uitgeput is bij hetgeen je zijn aantal noemt. Het aantal - zeg je ook - is een functie van de verzameling en wat je optelt en aftrekt zijn niet de verzamelingen maar hun aantallen. Het verband met de realiteit is dat hierbij aan het samenvoegen van gescheiden verzamelingen het optellen van hun aantal beantwoordt en aan het wegnemen uit een verzameling het aftrekken.
Hét verband? Neen, een verband, want optellen en aftrekken verantwoorden meer dan alleen maar dingmatig samenvatten en wegnemen. Als Jan evenveel knikkers heeft als Lies en Mies samen, wil dit niet zeggen dat die van Lies en Mies samen die van Jan opleveren; wel zegt het iets over de som van de functiewaarden. Als ik wil weten hoeveel knikkers Jan meer heeft dan Lies, kom ik er niet door van Jans knikkervoorraad iets weg te nemen wat hij niet eens heeft (te weten Lies' knikkers), maar door aantallen van elkaar af te trekken. Toch blijft de ‘deel - geheel-relatie’ in de onderwijskundige literatuur spoken - wat er aan schort gaan we later nog preciezer na.
| |
| |
Maar eerst nog eens het verschil tussen dingmatig en getalmatig optellen. Een halve kaas en nog een halve kaas opgeteld zijn twee halve kazen en niet een hele, ook al zijn het allebei Goudse en niet de één een Goudse en de andere een Edammer. Natuurlijk mag je van twee halve Goudse kazen ook één hele maken. Niet bij wijze van optellen maar bij wijze van aan elkaar plakken. Onderzoekers van onderwijs hebben daar niet altijd even heldere ideeën over, zoals uit het plaatje blijkt of uit een verhaal, waarbij hoofd, twee armen, romp en twee benen bij elkaar opgeteld als som een mens opleveren. Om op de kazen terug te komen, je kunt ze wel qua gewicht, volume en prijs bij elkaar optellen; dan gaat het echter niet om kazen maar om kaas, en analoog is het met onderdelen van het menselijk lichaam gesteld. Ook dit komt later nog aan de beurt.
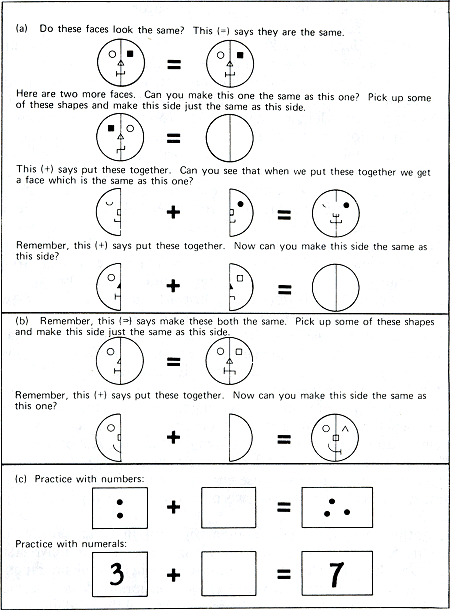
figuur 3.1
| |
| |
In spijt van de deel - geheel-relatie, die ondanks alle pogingen om uit te roeien voortwoekert, is 3 geen deel van 5. Bij het opzeggen van de getallenrij komt 3 vóór 5 en dat wordt als 3 < 5 genoteerd. Wel kun je twee verzamelingen maken zodat die met aantal 3 deel is van die met aantal 5 en zitten er in elke verzameling met aantal 5 ook verzamelingen met aantal 3 (en niet omgekeerd). Maar 3 peren zijn, hoe je het ook wendt of keert, geen deel van 5 pruimen en daar lopen bepaalde aftreksommen op stuk. 5 is meer dan 3, vijf pruimen is meer dan drie pruimen en als je wilt zijn 5 pruimen meer vruchten dan 3 peren. Als vijf meisjes en drie jongens bij elkaar zijn, dan zijn het meer meisjes dan jongens. Maar vraag niet: ‘Hoeveel meer?’ Althans niet aan jonge kinderen. Ze zullen er steevast op antwoorden: 5. Of vraag het ze wel, want ze moeten de taalkundige constructie ‘hoeveel meer, hoeveel minder’ (in alle talen die ik ken dezelfde gekke constructie) nog leren. Het is een taalkundig, geen rekenkundig probleem.
Meer of minder - soms kun je het met één oogopslag zien, maar ook dat kan en moet worden geoefend. Zo niet, dan ga je tellen. Een belangrijkere rol als initiërend element dan bij pure getallen spelen de vergelijkende trappen bij wat men noemt grootheden, juist omdat daar niet direct iets te tellen valt: groter - kleiner, langer - korter (ook van tijdsduur), zwaarder - lichter, ouder - jonger, warmer - kouder, duurder - goedkoper. Onze kinderen mogen zich gelukkig prijzen met dit taalverschijnsel vergeleken bij Franssprekenden, voor wie ‘plus’ en ‘moins’ de ene keer los en de andere keer gekoppeld aan een bijvoeglijk naamwoord, elkaar ernstig verstoren, zoals uit talrijke (Franstalige) Piaget-experimenten blijkt. Groter - kleiner, langer - korter enzovoort, ze hebben allemaal niets met een deel - geheel-relatie te maken of je moet er die met de haren bijslepen. De vergelijkende trap is een universeel taalmiddel om voorwerpen en verschijnselen volgens bepaalde kenmerken op een rijtje te zetten: mooier, zoeter, knapper, vervelender. Expres heb ik net voorbeelden gekozen, waarbij er niets te kwantificeren valt - niet eens in de zin van ‘hoeveel mooier’ enzovoort.
Grootheden zijn wel voor kwantificatie vatbaar, maar ook daar speelt de deel - geheel-relatie hoegenaamd geen rol. Of twee voorwerpen even lang zijn of welk langer is, constateer je door ze naast elkaar te leggen - direct of door bemiddeling van een derde - of op tal van andere manieren. Inhouden van glazen worden vergeleken door vloeistof van het ene in het andere te scheppen, volumes van voorwerpen door ze in een vloeistof te dompelen, ruilwaarden van voorwerpen door directe ruil of door ruil met geld. Net als aantallen functies zijn van verzamelingen, zijn grootheden functies van voorwerpen en verschijnselen: de lengte van een weg, de inhoud van een vat, de zwaarte van een voorwerp, de duur van een proces, de prijs van een waar.
Grootheden zijn, evenals getallen voor optelling vatbaar met als tegenhanger in de realiteit het samenstellen van wegen, het samenvoegen van vaten, het op elkaar aansluiten van tijdsaflopen, het bij elkaar rapen van waren. Tot zo ver is er ook hier van deel - geheel sprake. Maar daarmee kom je er bij lange na niet. Er moeten begrippen van gelijkwaardigheid (equivalentie)
| |
| |
bij of directer gezegd: methoden om voorwerpen of verschijnselen ten aanzien van bepaalde kenmerken aan elkaar gelijk te stellen - qua lengte, qua inhoud, qua zwaarte, qua duur, qua ruilwaarde. Daar hoeven nog geen getallen aan te pas te komen, zelfs niet bij het optellen. Twee landen zijn samen even groot als een derde; twee kinderen (op de wip) wegen samen evenveel als twee andere; twee zakken van dit zijn goedkoper dan drie zakken van dat.
Het verband tussen grootheden en getallen ontstaat doordat je gelijksoortige met elkaar meet. Hoeveel keer gaat de ene in de andere op? Het hoeft niet een geheel aantal keren en zodoende, bij het meten, melden de breuken zich aan. Hoe lang?, hoe zwaar?, hoe duur? wordt dan getalmatig beantwoord met een eenheidsmaat erbij, m, kg, ƒ of cm, ton, $ met ruilvoeten tussen gelijksoortige. Die kun je dan bij elkaar optellen en van elkaar aftrekken, zelfs om een voorbeeld van het begin op te halen: twee dubbeltjes aftrekken van drie kwartjes.
Tot nu toe heb ik me nauwelijks met notaties beziggehouden. Zoveel mogelijk heb ik alles in de omgangstaal geformuleerd.
4 + 3 =
lees je als ‘vier plus drie is’ en wat de ‘plus’ betekent wordt op diverse manieren uitgelegd. De ‘is’ betekent klaarblijkelijk dat je er moet achterzetten wat er uitkomt als de drie bij de vier wordt opgeteld. In vroegere tijden las je het dan ook ‘maakt’, ‘machen’, ‘font’, ‘facit’. De 4 en de 3 maken samen de 7.
Toen kwamen er de stipsommen zoals
4 + . = 7
hetgeen toen ik schoolging met een vraagteken in plaats van een stip werd geschreven en ‘4 plus hoeveel maakt 7’ werd gelezen. Waar de stipsommen goed voor waren, werd ons uiteraard niet verteld. De geschiedenis van de stipsommen zou nog eens geschreven moeten worden.
Ik vermoed dat ze uitgevonden werden, om redactiesommen van het soort ‘Jan had gisteren 4 knikkers en vandaag heeft hij er 7; hoeveel heeft hij er ondertussen bijgewonnen?’ te vergemakkelijken. Als dit zo is zijn ze inmiddels hun bestemming kwijtgeraakt. Niemand - boekjesschrijver, onderwijzer, leerling - legt nog verband tussen stip- en redactiesommen. Je zou natuurlijk kunnen eisen dat de leerling netjes onder
Jan is 4 en Piet 7 jaar
na de vraag
hoeveel is Piet ouder dan Jan?
de stipsom
4 + . = 7
en na de vraag
hoeveel is Jan jonger dan Piet?
de stipsom
7 - . = 4
plaatst. Het lijkt gezocht, maar er zijn er heus die menen dat didactiek bestaat in het berijden van dit soort stokpaardjes.
Inmiddels zijn stipsommen, zo niet in het onderwijs dan toch in het onder-
| |
| |
zoek van onderwijs, tot grote bloei geraakt. Het begon met het type
7 = 4 + .
waar de op gewone stipsommen getrainde kinderen geen raad mee wisten en na de nodige ‘successen’ van afgangen ging het door met
3 = . - 4
8 - 1 = 5 + .
5 + 2 = . - 1
. - 1 = 5 + 2
Het ontbreekt er nog aan dat die duizelingwekkende verscheidenheid gesystematiseerd wordt en met factor- en regressie-analyse statistisch te lijf wordt gegaan.
Hoe is de geschiedenis van de stipsommen nu in deze stroomversnelling geraakt? Om dit te verklaren, moet ik er heel wat bijhalen: de logische status van het ‘is’-teken.
Wiskundigen hebben de gewoonte van alles en nog wat een probleem te maken. Een lofwaardige gewoonte zolang je die problematiek binnen de perken houdt waar ze ontstaan is, althans niet in een onbeheersbare bosbrand laat ontaarden.
4 + 3
mag wel een ‘is’-teken vereisen als signaal om bij de 4 een 3 op te tellen, maar hoe is het dan met
a + b
gesteld, dat in de algebra opduikt? Een ‘is’-teken erachter? Wat valt er dan uit te rekenen als je noch a noch b kent? En die a + b kun je toch echt niet missen, als je naar (a + b)2 en ik weet niet wat nog allemaal toe wilt.
Algebra werd eens als letterrekenen onderwezen en a + b kwam inderdaad te pas in een lettersommetje zoals
(a + b)2 =
dat duidelijk aangaf wat hier gevraagd was, of ook in
a2 + 2ab + b2 =
waar het even duidelijk was, tenminste als de leraar het had uitgelegd. Leeftijdsgenoten die ik tegenwoordig ontmoet, vertellen me geregeld dat ze die sommen best konden doen, zonder de minste notie wat die letters betekenden.
Ik weet niet, wanneer dit voor het eerst als didactisch probleem werd opgevat, maar de generatie van mijn kinderen schijnt daar al meer weet van te hebben gehad: letters betekenden getallen, onbekende of onbepaalde of variabele - de functiegrafieken hebben daar wel toe bijgedragen. En ineens was het duidelijk wat
a + b
(met of zonder ‘is’-teken) betekende: als a en b zekere getallen zijn, is a + b ook een getal, te weten de som van a en b. En ineens trok de sluier op boven de hele letter-algebra. Dit inzicht, in de algebra verworven, ging nu in het tijdperk van New Math doorsijpelen naar het rekenonderwijs. Wat betekent 4 + 3? De voorwaarde ‘als a en b getallen zijn’ kun je hier laten vervallen want immers 4 en 3 zijn vanzelf getallen.
| |
| |
Dus het antwoord: 4 + 3, tot nu als som beschouwd, is een getal. Welk getal? Natuurlijk het getal 7. Natuurlijk? Waarom natuurlijk? Als 4 + 3 een getal is, waarom mag ik het niet 4 + 3 blijven noemen? Of 10 - 3, 21/3, √49? Het zijn immers niet, zoals je vroeger dacht, sommetjes, maar getallen. En toch ben je verplicht, er 7 voor te schrijven.
Ik had het al aangekondigd. Ik moet er heel wat bijhalen om de stroomversnelling van stipsommen te verklaren. Dingen - concrete of gedachte - roep je op met woorden, met hun namen. Feiten en kwesties omtrent die dingen roep je op met stellende en vragende zinnen, uit woorden opgebouwd, en deze zinnen zijn dan om zo te zeggen de namen voor die feiten en kwesties. Maar de taal is rijk (en soms ook arm). Er zijn dingen die je met een veeltal namen kunt oproepen (en andere waar je moeite mee hebt om ook maar één voor te verzinnen). Zodoende zijn er voor hetzelfde getal de namen 7, 4 + 3 21/3, √49 enzovoort en het is-teken houdt niets anders in dan dat aan weerszijden namen van hetzelfde ding staan.
Wat houdt zo'n schrijfsel als
4 + 3 = 7
dan in? Hoegenaamd niets. Aan weerszijden staan namen van hetzelfde ding. En voor zover 4 + 3 = 7 in al zijn bescheidenheid representatief mag zijn voor de diepste wetenschap, zou je kunnen zeggen dat al onze kennis erin bestaat uiteenlopende namen te verzinnen of te hebben verzonnen voor dezelfde dingen.
Maar het is evenzeer duidelijk, dat hier iets niet in de haak is.
De graaf die in 1296 op het Muiderslot werd vermoord = Floris V,
De man op Fr. Schubertstraat 44 in Utrecht = schrijver dezes,
De moordenaar van... =... (vul bij de stippeltjes iets in)
‘De vierkleurenhypothese klopt’ = waar,
ziedaar overal rechts en links van het is-teken namen voor hetzelfde object, maar - helaas - om dit feit te verifiëren moet je geschiedeniskennis, of je adreslijst, of de recherche of de computer er aan te pas komen.
Zo eenvoudig was het dus niet. Wat bij taaluitingen telt is, naast hun formele structuur, hun intentie. Naast? Neen, allereerst. Zinsontleding, taalontleding is iets van een hogere plank dan van een taaluiting de intentie te begrijpen.
4 + 3 =
brengt een intentie over, die van een sommetje. De logische analyse van
4 + 3 = 7
noemde ik iets van een hogere plank. Dus iets om naar toe te groeien. Met een trapje zou je er uiteraard ook bij kunnen komen of je laat je eventjes optillen. Dat bedoelden de welmenende schoolboekauteurs uit het voorbije tijdperk van New Math. Je bracht kinderen - liefst als kleuters - als bedoeling van het is-teken bij dat aan weerszijden ‘hetzelfde’ zou staan. Het leek zinsontleding oefenen met een kind dat net leert praten. In de onderwijskunst is dit al weer van de baan, maar inmiddels zijn onderwijskunde en -psychologie erdoor gegrepen als door een openbaring.
| |
| |
Een bezwaar van verklaringen van de bovenste plank is, dat ze op normale leefhoogte (en zeker op die van het lerende kind) niet operationeel zijn. Je moet je er toch tegen kunnen wapenen dat 4 + 3 = wordt beantwoord met - lekker! -
4 + 3 = 3 + 4
of - nog brutaler -
4 + 3 = 4 + 3.
De New Math-ers hebben er toen iets op uitgevonden. Boven zo'n stel sommen zetten ze:
Vul in de standaardnamen van...
Inderdaad, onder de namen waarmee je getallen of andere concrete of gedachte objecten kunt oproepen, zijn zekere voorkeurnamen, om zo te zeggen, de namen waaronder je voor het eerst met ze kennis hebt gemaakt. ‘7’ is de standaardnaam van wat je later ook tegenkomt in 4 + 3, 10 -3, 21/3, √49. ‘Standaardnaam’ is natuurlijk geen wiskundig begrip. Het is een pragmatisch begrip. ‘Namen voor hetzelfde ding aan weerszijden van het is-teken’ is onberispelijke taal, maar als je op 4 + 3 = het antwoord 7 wenst, moet je je voorkeur voor standaardnamen kenbaar maken, met een beroep op de welwillendheid van de goede verstaander die je voorkeur kent en billijkt.
‘Zo moet het van de meester’ is zo gek nog niet, al wordt de meester later een meneer, een schoolboekauteur of een toetsenbakker.
Maar laten we dan de verklaring van de bovenste plank aanvaarden dat aan weerszijden van het is-teken ‘hetzelfde’ staat, alleen met verschillende namen opgeroepen. Is dan behalve
4 + 3 = 7
ook
4 m + 3 m = 7 m
4 kg + 3 kg = 7 kg
4 ct + 3 ct = 7 ct
gerechtvaardigd? Ja, want 4 m stelt geen staf, 4 kg geen metalen gewicht en 4 ct geen stel van 4 centen voor (en overeenkomstig met de 3 en 7). Het zijn lengtematen, gewichten, geldwaarden. En hoe is het met
4 knikkers + 3 knikkers = 7 knikkers
gesteld? Jan heeft 4 knikkers en Piet heeft er 3 meer; hoeveel heeft Piet dan? Daar klopt iets niet. Het begint trouwens al eerder, met
4 knikkers = 4 knikkers.
Die vier van Lies zijn toch niet dezelfde als die van Mies. Maar de wiskundige die dit kromme is-teken recht moet praten, laat zich voor geen gat vangen. Hij heeft er iets op uitgevonden dat altijd werkt. Hij vormt wat je noemt de klasse van alle viertallen knikkers (en voor dat soort klassen een optelling) waar ‘vier knikkers’ dan een naam voor is om op te roepen en dan staat weer rechts en links van het is-teken hetzelfde, ook bij
4 knikkers + 3 knikkers = 7 knikkers.
Het is nu zelfs iets van de allerbovenste plank, maar ik wilde het u toch niet onthouden.
| |
| |
Van een leerling die nooit eerder een stipsom is tegengekomen, kun je niet verwachten, dat hij de bedoeling van
4 + . = 7
begrijpt. In de vorm
wat stond er in
onder de inktvlek?
is de opdracht tenminste zelfverklarend. Maar een type zoals
7 = 4 + .
is ook in de vorm
wat stond er in
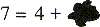onder de inktvlek?
niet zelfverklarend als de leerling nooit eerder schrijfsels zoals
7 = 4 + 3
is tegengekomen. Voor de onderzoeker is gelukkig het feit dat het kind
7 = 4 + 3
niet als even vanzelfsprekend beschouwt als
4 + 3 = 7
het bewijs dat het is-teken niet begrepen is. Het is-teken, wel te verstaan, van de wiskunde van de bovenste plank. Daar kun je dan het kind naar toe optillen door met hem het ‘omdraaien’ van gelijkheden systematisch te oefenen. Zelfs van een gelijkheid zoals
7 = 7
als je maar de ene 7 rood en de andere groen schrijft.
Ik bedoel hier geenszins mee uitdrukkingen zoals
7 = 4 + 3
taboe te verklaren en evenmin hieraan beantwoordende sommetjes. Er kan wel degelijk behoefte aan zijn, maar dan niet één, ingegeven door een dogmatisme omtrent de betekenis van het is-teken. Op den duur moet het kind rekenkundige uitdrukkingen los van enige context kunnen hanteren, maar als instap verdient context de voorkeur boven formele aanwijzingen (in casu: ‘draai de vergelijking om’). En die context is er: Als 7 personen zich over twee auto's moeten verdelen, kan
7 = 4 + 3
een natuurlijke symboliek hiervoor zijn. Trouwens ook
7 = 3 + 4
dat misschien een ander gebeuren beschrijft. Ook
7 = 5 + 2
kan aannemelijk zijn, terwijl aan
7 = 6 + 1
een heel verhaal te pas komt en zeer zeker aan
7 = 7 + 0.
Ook naar de (paradigmatische) equivalentie van
4 + 3 = 7 en 7 = 4 + 3
hoeft men niet via papieren eigenschappen van het is-teken toe te stappen, maar door bijvoorbeeld aan één keer de samenvoeging van twee blokkentreintjes van 4 en 3 en de andere keer de splitsing van één blokkentrein van 7 te symboliseren.
Voor aftreksommen kan men iets dergelijks verzinnen. Een moedereend
| |
| |
met 4 kleintjes kan uit een nest komen van 7 waar 3 van dood zijn gegaan en dat wordt dan door
4 = 7 - 3
beschreven, maar misschien was het ook
4 = 8 - 4
of... ga zo maar door. En je kunt er vragen aan vastknopen zoals ‘en als het eerst 10 zijn geweest?’ of ‘en wanneer er 5 zijn doodgegaan?’
Het kan nog ingewikkelder:
Als Jan 8 en Piet 4 knikkers heeft, wat moeten ze onderling doen om evenveel te hebben?
Of
... opdat Jan 2 meer heeft dan Piet?
En hoe is het met
... Jan 3 meer dan Piet
gesteld?
Als je desondanks op de symmetrie van het is-teken af wilt, beschik je over andere taalmiddelen om ‘éénrichtingsverkeer’ te symboliseren, bijvoorbeeld de pijlentaal. Vooral in dynamische situaties is dat doeltreffend: Bussen met haltes waar in- en úitgestapt wordt, kegels die omgegooid of opgezet worden, voorraden die slinken en aangevuld worden.
+ 3
4 → 7
kan veelvuldig geïnterpreteerd worden of omgekeerd als beschrijving van velerlei gebeurtenissen dienen. Handelingstaal is oorspronkelijker dan statische taal. De lezing
vier plus drie
voor
4 + 3
is eigenlijk ‘fout’. Wiskundige puristen moeten dit lezen als
som van 4 en 3
en in de zogenaamde Poolse notatie is het dan ook
+ (4,3).
Als je iemand de weg wilt wijzen, zeg je bijvoorbeeld: ‘Bij het tweede stoplicht rechts af, dan de tweede zijstraat links tot het stoplicht en dan rechts af’ en niet ‘rechter zijstraat bij het stoplicht van de tweede linker zijstraat bij het tweede stoplicht.’
Pijlentaal of niet - optellen en aftrekken zijn handelingen en die moet je leren beheersen eer je naar ‘som’ en ‘verschil’ toegroeit.
| |
| |
| |
Terug- en vooruitblik
Hoeveel valt er niet over het is-teken te zeggen en moet dit allemaal? Onderwijskundigen en psychologen hebben gemeend dit onderwerp van de hoogste wiskundeplank naar beneden te halen. Dit opstel werd geschreven om de leerling tegen deze wijsheid te beschermen en de onderwijzer en ontwikkelaar voor de angstcomplexen te behoeden of hij het wel goed doet. Ga even in diverse rekenmethodes na hoe simpel of hoe geleerd ze dit probleem, vooral in verband met stipsommen, aanpakken. Kijk ook naar handleidingen en, als u ze tegenkomt, naar theoretische uiteenzettingen, om de kritiek toe te passen.
Op dit zeer speciale onderwerp volgt er een van zeer algemene strekking, maar dan in de context van zeer concrete voorbeelden.
|
|
Auteursrechtelijk beschermd