Logo DBNL
De Zeventiende Eeuw. Jaargang 12 (1996)

De Zeventiende Eeuw. Jaargang 12

(1996)– [tijdschrift] Zeventiende Eeuw, De–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

Huygens's 1688 Report to the Directors of the Dutch East India Company
on the Measurement of Longitude at Sea and its Implications for the Non-Uniformity of Gravity
Eric Schliesser and George E. Smith

Summary

When Huygens prepared the 1686-87 expedition to the Cape of Good Hope on which his clocks would be tested for their usefulness in measuring longitude at sea, he also gave instructions to Thomas Helder to perform experiments with the seconds-pendulum. His goal was to check Richer's finding that a seconds-pendulum is 1¼ lines (2.8 mm) shorter in Cayenne than it is in Paris. Unfortunately, Thomas Helder died on the voyage to the Cape of Good Hope, and no data from the seconds-pendulum ever reached Huygens. He nevertheless did receive data from his clocks on the return-voyage from the Cape of Good Hope to Texel. When he first calculated the ship's course according to these data, it appeared to have gone straight through Ireland. He then tried introducing a correction to the data, based on an idea he had been entertaining as a possible explanation of Richer's finding. Specifically, he corrected the observed time to compensate for a reduction in the effect of gravity at the Equator caused by the Earth's rotation. His newly calculated course convinced him that this rotational effect is the sole source of any variations in gravity with latitude. This paper examines Huygens's corrections to the data and his reasoning from the new course to the conclusion that nothing else is causing a variation in gravity. In the process, we will show that Huygens appeared to have good empirical reasons to reject Newton's theory of universal gravity, which predicted a slightly larger variation in gravity.

Introduction

Christiaan Huygens published his Discourse on the Cause of Weight as an addendum to his Treatise on Light in 1690.1. The Discourse consists in part of an old work, ‘On the Cause of Gravity’, that he had first presented to the French Academy in 1669, a brief middle part he probably wrote in 1686 or 1687, and an ‘Addition’ he wrote after he had read Newton's Principia.2. The first paragraph of this ‘Addition’ refers not only to Newton's Principia, but also to his own (1688) ‘Report to the Directors of the Dutch East India Company on the Measurement of Longitude at Sea’3. (hereafter, the ‘Report’).

ADDITION
Some time after I had finished writing the preceding, [I] received and examined the journal of the voyage, which by order of the Directors of the Dutch East India Company, had been made with our pendulum Clocks as far as the Cape of Good Hope;
and since then [I] have also read the very scholarly work of M. Newton, entitled Philosophiae Naturalis principia Mathematica. Both of these provided me with material to extend this Discourse further. First, as for the different lengths of the Pendulums in different Climates, which he has also treated, I believe to have, by the average of these Clocks, not only a clear confirmation of the effect of the motion of the Earth but also of the measure of these lengths, which agrees very well with the calculation that I have just given. For, having corrected and adjusted, following this calculation, the Longitudes that were measured by the Clocks on the return from the Cape of Good Hope to Texel in Holland (because going they were not of service), I have found that the route of the vessel was much better marked on the Map than it would have been without this correction; so much so, that arriving at this Port, there was not 5 or 6 leagues of error in the Longitude thus adjusted. Supposing that the aforementioned Cape had been well surveyed by the Jesuit Fathers when they passed there in the year 1685, going to Siam; and that it is some 18 degrees more to the East than that of Paris, which I know yet moreover to be scarcely far from the truth. The detail of this affair is deduced in full in the Report that I have made concerning this voyage of the Pendulums to said Directors. As for this report, after it had been examined by intelligent persons, it pleased them to direct us to make a second test in order to be assured by several experiments of the soundness of this discovery. We will see what the success of this other voyage will be and particularly what the variation of the Pendulums is, being certain that, in order for [the variation] to be known well, these Clocks give an average more certain, by their acceleration and deceleration, than actually measuring the length of the Seconds pendulum in different countries. Meanwhile, because experience in the trial of which I have been speaking is so well in accord with what I have found by reasoning, I trust enough in this to wish to continue this speculation, considering first what the figure of the Earth is, since, as has been said, it is not Spherical.4.

The most important feature in this paragraph is Huygens's claim that the Report not only confirms the rotation of the Earth - this by showing that the rotation necessitates a correction to his clocks at sea - but also establishes the precise amount the seconds-pendulum has to be shortened at different latitudes. Huygens had two claims at stake in the voyage discussed in the Report: first, that his clocks could be used to determine longitude at sea; and, second, that the secondspendulum provided a universal, invariant standard of length.5. In effect, the voyage discussed in the Report had shown him that the second of these claims requires modification because the Earth's rotation reduces the net effect of gravity at the Equator versus the Poles, thereby requiring the seconds-pendulum to be shorter at the Equator. This is the first major conclusion from the Report. The second is that the Earth's rotation is the only source of any such variation in gravity, so that by taking it into account the precise length of the seconds-pendulum at each latitude could be calculated once and for all, given the length at Paris.

Strangely, the Report was never published, nor was it translated into French or Latin. We have found no evidence Huygens tried to circulate it among scientists, other than its review by two Dutch contemporaries, Hudde and de Volder.6. This raises the suspicion that perhaps the evidence of the Report was not so compelling as the paragraph quoted from the Discourse suggests. The questions we will be examining here are 1) what exactly was Huygens's evidence that the Earth's rotation and it alone affects the length of the seconds-pendulum?; and 2) how good was this evidence?

Measuring the Length of a Seconds-Pendulum

The Report contains a discussion of the performance of Huygens's experimental sea clocks on a voyage commissioned by the Dutch East India Company. In 1686 two of Huygens's clocks were placed aboard the ship Alcmaer in order to test their accuracy in measuring longitude at sea.7. Two of Huygens's assistants, Thomas Helder and Johannes de Graaf, were to accompany the clocks from Texel to the Cape of Good Hope and back. Huygens's Report is based on data collected by de Graaf and the ships' mariners during the return voyage. Unfortunately, Thomas Helder died on the return voyage, and many of his notes disappeared, denying Huygens some potentially crucial further evidence. The Report, written in Dutch, was sent to the Dutch East India Company on April 24th, 1688.

As Huygens remarked in a letter of 1 May 1687 to de la Hire, while the Alcmaer was still at sea and a few weeks before he received his copy of Newton's Principia, the question of the length of the seconds-pendulum was quite confusing at the time.8. As Table 1 shows, Huygens, Richer, and Varin, DesHayes, and de Glos had all obtained virtually the same value for the length of the seconds-pendulum in Paris, within 1/10th of a line.9. Thus, we can surmise a level of accuracy in measuring the length of the pendulum of about a tenth of a line - something that would have been difficult to achieve with the naked eye, but was possible using minor magnification. The good agreement between the acceleration of gravity implied by the measurements in Paris and our modern measured value adds support for this level of accuracy.

TABLE 1. MEASURED LENGTHS OF THE SECONDS-PENDULUM AS OF 1684
LOCATION LATITUDE LENGTH (Paris units) IMPLIED g (cm/sec2)
HUYGENS Paris 48o50′ 3ft 8½ lines (980.7)
RICHER Paris 48o50′ 3ft 8⅗ lines (980.9)
  Cayenne 4o55′ Δl = 1¼ lines (978.1)
VARIN et al Paris 48o50′ 3ft 8 5/9 lines (980.7)
  Goree 14o40′ Δl = 2 lines (976.4)
  Guadaloupe 15o00′ Δl = 2 1/18 lines (976.3)
 
NB. Modern measured g at Paris = 980.970 cm/sec2.
Modern average g at Equator = 978.032 cm/sec2.

In 1672 Richer had found that the seconds-pendulum had to be shortened by 1 and 1/4 lines in Cayenne, just north of the equator.10. Ten years later Varin et alia found that the seconds-pendulum had to be shortened by 2 lines in Goree, just off Cape Verde, ten degrees farther north from the equator than Cayenne, and they found an even larger correction was needed in Guadeloupe and Martinique.11. Huygens had reasons to find these measured lengths of the seconds-pendulum confusing even beyond their conflict with one another. From his previous work on centrifugal force he had calculated that the centrifugal effect of the Earth's rotation at the equator is 1/289th of the force of gravity. From this, he could readily calculate how

much the seconds-pendulum had to be shortened at every latitude if the centrifugal effect of the Earth's rotation, and only it, was altering local effective gravity.12. In particular, as Table 2 indicates, rotation alone would necessitate a shortening of the seconds-pendulum at Cayenne 4/10 of a line less than Richer had found, and a shortening at Goree almost 1 and 1/4 lines less than Varin et alia had found. Admittedly, all of these differences in length are impressively small to be attaching great significance to. Huygens must have given some thought to dismissing them as resulting from careless measurement.13.

TABLE 2. MEASURED VARIATIONS IN GRAVITY VERSUS THE VARIATIONS INFERRED BY HUYGENS
MEASURED FROM ROTATION ALONE
LATITUDE Δl %CHANGE Δl %CHANGE
RICHER  
Paris- 48o50′ 1.25 lines 0.284 0.852 lines 0.194
Cayenne 4o55′ (2.82 mm)   (1.92 mm)  
 
VARIN et al  
Paris- 48o50′ 2.00 lines 0.456 0.774 lines 0.176
Goree 14o40′ (4.51 mm)   (1.75 mm)  

Huygens had another reason to distrust the measurements. He knew that the arc of the seconds-pendulum had to be kept quite small in order for it to provide a meaningful measure of the strength of local gravity. When proposing the secondspendulum as a universal standard of length in the Horologium Oscillatorium,14. he specifically warns that the length will not be correctly determined if the total pendulum arc exceeds 5 or 6 degrees. In Richer's brief paragraph on the subject he tells us that he had kept the arc very small, but not how small.15. An excess arc length could easily explain the notably greater changes in length found by Varin et alia.16. So, Huygens had good reason to want new pendulum length measurements to be made at various locations. As he remarks in the middle section of the Discourse, the measurements that had been made before 1686 should be looked on as providing only rough initial data.17.

It should come as no surprise, then, that when the Alcmaer expedition was being prepared, Huygens not only wrote elaborate and precise instructions for the installation and handling of his clocks,18. but he also gave detailed instructions to Helder for measuring the length of the seconds-pendulum along the course of the voyage.19. Huygens explicitly instructed Helder not to let the arc of the pendulum become larger than 2 or 3 thumbs - i.e. 2 or 3 Rhenish inches - which would have kept any discrepancy in the length of the seconds-pendulum below 1/10 of a line. If Helder ever performed any experiments with the seconds-pendulum during the voyage, Huygens never received data from them.20. Helder died shortly after the departure from the Cape of Good Hope, and although Huygens requested Helder's notes,21. we have no indication he received all of them. Regardless, the only useful data Huygens received from the Alcmaer's journey were on the performance of the clocks on the return-voyage from the Cape of Good Hope to Texel.22. Fortunately,



illustratie
1. The first page of the table of Hugens's calculations in the Report.


de Graaf took over the observation of the clocks shortly after Helder died and monitored the clocks all the way back to Texel, where the Alcmaer arrived on August 15, 1687.

The 1688 Report

De Graaf's journal and the logbook of the Alcmaer's mariners provided Huygens with enough material to compare the course of the ship as determined by the mariners with both the course as determined from the longitude implied by his clocks and the course implied by his clocks after they had been corrected to account for the effects of the Earth's rotation. The table Huygens presents in the Report, the first page of which is shown in Figure 1, has ten columns. Column I gives the date. The first day the clocks were used to determine longitude was May 10. Column II gives the latitude as determined by the ship's mariners. Column III gives their estimates of the ship's longitude, restated in Column IV as longitude west of the Cape of Good Hope. Column V shows the longitude of the ship according to the clocks in hours west of the Cape. Column VI shows the theoretical amount the clocks were losing each day, also known as the largest daily delay, versus the time they would keep at the north and south poles - this as a consequence of the lessening of effective gravity from the Earth's rotation. Column VII then gives the net time the clocks have theoretically fallen behind what they would have shown had they remained at the Cape. This Column is calculated by adding all of the largest daily delays and then subtracting for each day the corresponding largest daily delay at the Cape. Thus, on May 10, from the Earth's rotation alone the clock theoretically would have fallen behind by 6 minutes and 42 seconds versus what it would have



illustratie
2. Huygens's map comparing his uncorrected and corrected courses with the mariners' course.


shown at the Cape. Adding this amount to the longitude as indicated by the clock gives the corrected longitude, in hours west of the Cape, as shown in Column VIII, and in degrees, as shown in Column IX. Column X then gives the difference between Columns IV and IX, that is the difference between the mariners' course and the course as calculated from the clocks after the correction for the Earth's rotation is included.

Huygens laid these three courses out on a map accompanying the report, shown in Figure 2. The course lying farthest to the west in the Atlantic is the one estimated by the mariners. The one a little to the east of it is the course determined by the clock after the correction for the Earth's rotation had been included. And the course lying farthest to the east is the one determined by the clock without the correction. The latter course goes straight through the middle of Ireland. This alone was strong evidence that some correction to the clock was needed. The comparison between the mariners' course and the course with the correction to the clock is reasonably good along the entire northward leg of the voyage. Huygens knew from the sea-trials of his clocks in the 1660s that the mariners' course was not necessarily more accurate than one based on his clocks, so that the discrepancies shown in the Atlantic were no cause for concern.23.

The same cannot be said, however, of the discrepancies in the southward leg from the tip of Scotland to Texel. Huygens had good reason to reject the mariners' course for this part of the voyage. It was clearly based on longitudes shown on their map for the tip of Scotland and the islands nearby. This map was not reliable, as it indicated Texel was 15 degrees 30 minutes west of the Cape of Good Hope. In 1685 Father Tachard, a Jesuit, had established the longitude of the Cape of Good Hope by using the eclipses of the moons of Jupiter as predicted by Cassini's tables.24. Based on Tachard's observations, Huygens concluded that Texel is 14 degrees 25 minutes west of the Cape.25. This gave him grounds for discounting the comparatively large discrepancies shown on the map for this leg of the voyage.

More importantly, the comparison of this independently established difference in longitude between the Cape and Texel and the difference obtained from the clocks along the voyage gave Huygens his strongest evidence for concluding that the only variation of gravity is from the Earth's rotation.26. At the end of the 118 day voyage, with the correction to the clock accumulating the entire way, the calculated location of Texel is only 17 minutes of arc to the east of the location based on Tachard's observations. This is a mere 19 km. In terms of deviations in the clocks from unaccounted for sources, it represents only 68 seconds accumulated loss over 118 days. Huygens thus had good reason to claim that, once his clocks were corrected to account for the Earth's rotation, they could be used to determine longitude at sea accurately.

An Assessment of Huygens's Evidence

How good then was Huygens's evidence for his two basic claims? The course in the Atlantic, as well as the good agreement for Texel, provide compelling evidence that some correction to the clocks is needed - or, equivalently, that the length of the seconds-pendulum is not invariant with latitude. But the comparison between

the mariners' course and the course based on the corrected clock is not enough to show that the only correction needed is the one for the Earth's rotation. The mariners' course is not that reliable. Therefore, the comparison at Texel must provide the principal evidence that the only correction needed is for the Earth's rotation.

It was entirely within Huygens's reach to recalculate the corrections to the clock based on Richer's measured length of the seconds-pendulum at Cayenne, Varin's measured length at Goree, or, for that matter, Newton's theoretical prediction of the variation of gravity with latitude, inferred from his theory of universal gravity. Huygens could easily have calculated the largest daily delay of the clock from the pole to the equator on any of these bases.27. He had used 2 minutes 30 seconds in the table in the Report, having rounded from the theoretical value of 2 minutes 29.35 seconds. Based on Richer's measurement at Cayenne, the delay would have been 3 minutes 38 seconds; based on Varin's Goree measurement, the delay would have been 6 minutes 31 seconds; and based on the first edition of Newton's Principia, 3 minutes 7 seconds. Given the method Huygens used in calculating the local daily delays in his table, which involved a minor simplification, all he had to do was to scale the cumulative corrections to the clocks at each point where longitude was found along the course to obtain new corrections corresponding to these other assumptions.28. Specifically, a course based on Richer's measurement could be determined simply by scaling all of the corrections by a factor of 1.455; on Varin's measure, by a factor 2.607; and on Newton's theory, by a factor of 1.247. We do not know whether Huygens took the trouble to do these calculations, but he certainly could have; and even if he didn't it would have been trifling for him to have estimated the magnitudes of the differences in his head.

A course based on Varin's measurement is the one far to the west on the map shown in Figure 3. It lies even farther to the west of the mariners' estimated course than Huygens's original uncorrected course lay to the east. However inaccurate the mariners' estimated course may have been, it was unlikely to have been this bad. Furthermore, a course based on Varin's measure would have placed Texel only 9 degrees 30 minutes west of the Cape - almost 5 degrees farther east than Huygens's calculated course had located it. This is more than 329 km to the east of the location of Texel based on Tachard's observations. Hence, this calculation would have given Huygens decisive grounds for rejecting any systematic corrections to the clocks based on Varin's measurement of the length of the seconds-pendulum in Goree. If the lengths measured by Varin et alii in Goree and Guadeloupe were correct, gravity must vary locally in wild ways not reflected by the clocks during the return voyage from the Cape.

As Figure 4 shows, the evidence is less decisive in the case of a course recalculated on the basis of Richer's Cayenne measurement. A course based on Richer's measurement, shown just west of the mariners' course at the equator on the map, is relatively close to the mariners'. In some places it is a little farther to the west of the mariners' course than Huygens's course is to the east of it, but at several places a course based on Richer's measure is even closer to the mariners' than Huygens's is. So, the course in the Atlantic does not provide any compelling reason for rejecting Richer's measurement of the seconds-pendulum in Cayenne.

The comparison at Texel, however, seems more decisive. Correcting the course



illustratie
3. The course using corrections based on Varin's measurement in Goree.




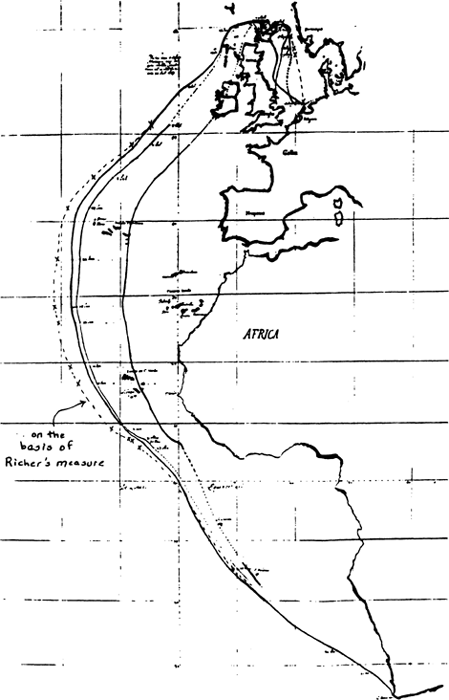
illustratie
4. The course using corrections based on Richre's measurement in Cayenne.


on the basis of Richer's measurement places Texel 12 degrees 50 minutes west of the Cape of Good Hope, 1 degree 35 minutes to the east of the location Huygens had inferred for it from Tachard's observations. This amounts to a discrepancy of 106 km, nearly 6 times that of Huygens's corrected course. So, this calculation would have given Huygens strong grounds for thinking that Richer's difference of 1 and 1/4 lines in the length of the seconds-pendulum in Cayenne was excessive.

TABLE 3. HUYGENS'S THEORY VERSUS NEWTON'S.
HUYGENS NEWTON
LATITUDE Δl %CHANGE Δl %CHANGE
Paris- 48o50′ 0.852 lines 0.194 1.068 lines 0.242
Cayenne 4o55′ (1.92 mm)   (2.41 mm)  
 
Paris- 48o50′ 0.744 lines 0.176 0.972 lines 0.221
Goree 14o40′ (1.75 mm)   (2.19 mm)  
 
Pole-Equator} Maximum  
Pole-Equator} Daily 2m 30s 3m 7s
Pole-Equator} Delay  
 
NB. I.e., rotation alone versus universal gravity for uniformly dense Earth (as in the 1st edition of Newton's Principia).

Finally, since Huygens had read the relevant parts of the Principia when he wrote the 1688 Report29., he had some reason for wanting to compare the correction based on rotation alone with a correction based on Newton's theory of universal gravity. In the first edition of the Principia, Newton gives the amounts the secondspendulum has to be shortened in Cayenne and Goree on the basis of his theory.30. Table 3 compares these values with Huygens's. The amounts in both cases are larger than the correction from rotation alone, but not so much larger as those implied by the Richer and Varin measurements. Specifically, Newton's theory gives a value for the shortening of the seconds-pendulum about midway between Richer's measurement and the value Huygens had obtained on the basis of rotation alone. The question is what the course from the Cape of Good Hope to Texel would have looked like using Newton's value for the largest daily delay from the Pole to the Equator of 3 minutes and 7 seconds instead of Huygens's value of 2 minutes 30 seconds.

In general, as Figure 5 shows, the leg of the Alcmaer's course in the Atlantic based on Newton's theory lies even closer to the mariners' course than Huygens's corrected course did. So a comparison of this part of the course would have given Huygens no grounds for claiming that a correction based on rotation alone was more accurate than a correction based on Newton's theory, which included not only the effects of rotation, but also a variation in local gravity from the non-sphericity of the Earth as implied by the law of universal gravity.

 

The comparison at Texel, however, did provide Huygens with some grounds for claiming that the correction based on rotation alone is more accurate than one



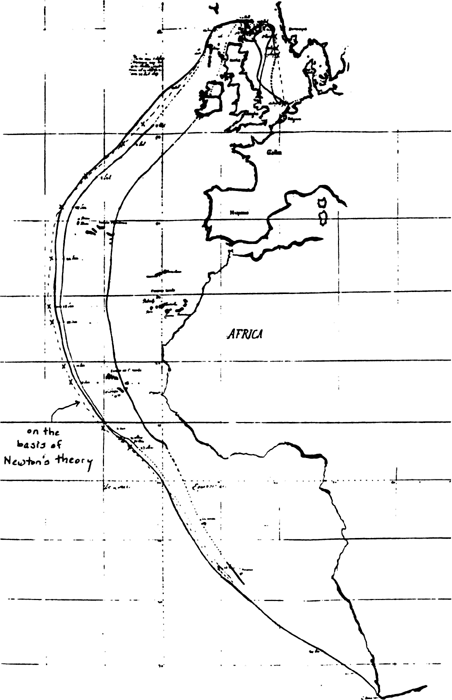
illustratie
5. The course using corrections based on Newton's theory of gravity.


based on Newton's theory. A calculated course based on Newton's theory locates Texel at 13 degrees 26 minutes west of the Cape of Good Hope, which is 59 minutes to the east of its location based on Tachard's observations. This is almost 66 km east, as compared to Huygens's value of 19 km. So, Newton's theory seems to be entailing too large of a correction - i.e. the amounts by which he is saying that the seconds-pendulum has to be shortened at Cayenne and at Goree are too great.

TABLE 4. DISCREPANCIES IN THE LONGITUDE OF TEXEL BASED ON CORRECTIONS TO THE LONGITUDES FROM HUYGENS'S CLOCKS AND THE VALUE BASED ON TACHARDS'S LONGITUDE OF THE CAPE.
WITH CORRECTIONS TO THE ALCMAER'S COURSE DISCREPANCY IN LONGITUDE DISCREPANCY IN KM
Based on rotation alone 0o17′ E 19.0
Based on Varin's Δl in Goree 4o55′ E 329.7
Based on Richer's Δl 1o35′ E 106.2
Based on Newton's theory 0o59′ E 65.9

We can now reconstruct the argument Huygens could have offered for claiming that the only mechanism causing the length of the seconds-pendulum to vary is the Earth's rotation. A course based on the hypothesis of rotation alone placed Texel very near the location that Huygens had independently established on the basis of Tachard's observations. Huygens could have easily calculated courses based on hypotheses corresponding to Richer's and Varin's measurements and Newton's theory. Indeed, he would not have had to perform the calculations to see the qualitative contrast shown in Table 4. If he, or anyone else, did the calculations, they would have found that each of these alternative courses would place Texel significantly farther to the east of the location established with Tachard's measurements. Thus, the calculations would have shown that any correction greater in magnitude than the one for rotation alone would have produced an excess discrepancy. All the evidence available to Huygens accordingly favored rotation alone over these alternatives to it. Given the questions about the measurements made by Richer and Varin et alii, not to mention those concerning Newton's theory, Huygens could have argued that the evidence from the voyage should take precedence. As he said in the first paragraph of the ‘Addition’ to the Discourse, the cumulative effects of the alternative corrections over the 118 days of the voyage should have had the virtue of amplifying the small differences among the competing claims about the length of the seconds-pendulum.

The conclusion we are reaching about the evidence available to Huygens is more important than it may at first seem. A close reading of Newton's Principia shows that the only clear empirical contrast it was offering between inverse-square gravity among celestial bodies and universal gravity among all particles of matter was the variation of surface gravity with latitude, coupled with the extent of the oblateness of the Earth. Newton's theoretical derivation of the lengths of the seconds-pendulum in Cayenne and Goree in the first edition of the Principia presupposed universal gravity. Huygens was prepared to accept inverse-square celestial gravity on the basis of the Principia, but he had well known philosophical objections to universal

gravity. The lengths of the seconds-pendulum measured in Cayenne and Goree, however, could have been offered as empirical evidence for universal gravity. Newton, indeed, could be interpreted as having done so. But the voyage from the Cape of Good Hope to Texel was providing Huygens grounds for discounting these measured lengths. As he remarked in the first paragraph of the ‘Addition’ to the Discourse, the voyage was showing that the observed variations in the length of the seconds-pendulum were evidence only for the rotation of the Earth. The voyage provided an empirical basis for challenging any claim to their being evidence for universal gravity. As our reconstruction suggests, Huygens did not have to appeal to philosophical arguments alone in rejecting it. It is presumably this evidence Leibniz had in mind when he wrote Conti in December of 1715: ‘I am strongly in favor of the experimental philosophy but M. Newton is departing very far from it when he claims that all matter is heavy (or that every part of matter attracts every other part) which is certainly not proved by experiments, as M. Huygens has already properly decided...’31. From Huygens's and Leibniz's point of view, the only empirical evidence that Newton had offered to support the step from inversesquare celestial gravity to universal gravity had been shown by the voyage not to be evidence at all.

The Tachard Measurement

Unfortunately, the evidence for Huygens's conclusion was not as good as our reconstruction suggests. The problem lies in the error in the location of Texel that Huygens inferred on the basis of Tachard's observations. Once we use the modern value for the longitude of Texel relative to the Cape, we find Huygens's course placing it 25 minutes to the west; a course based on Newton's theory, 17 minutes to the east; a course based on Richer's measurement 53 minutes to the east, and a course based on Varin's measurement 4 degrees 13 minutes to the east. In other words, as shown in Table 5, the true location of Texel lies between a course based on Newton's theory and Huygens's course based on rotation alone; and the course based on Richer's measurement places Texel not that much farther to the east than Huygens's course places it to the west.

TABLE 5. A COMPARISON OF THE DISCREPANCIES IN THE LONGITUDE OF TEXEL USING THE VALUE HUYGENS INFERRED FROM TACHARD AND OUR MODERN VALUE FOR TEXEL.
USING TACHARD VALUE USING MODERN VALUE
DISCREPANCY DISCREPANCY
WITH CORRECTIONS TO THE ALCMAER'S COURSE LONGITUDE KM LONGITUDE KM
Based on Huygens 0o17′ E 19.0 0o25′ W 27.9
Based on Varin's Δl 4o55′ E 329.7 4o13′ E 282.8
Based on Richer's Δl 1o35′ E 106.2 0o53′ E 59.2
Based on Newton 0o59′ E 65.9 0o17′ E 19.0

Huygens, of course, had no way of knowing this. If he had known the modern value for the location of Texel, he would still have had strong grounds for rejecting Varin's measurement. But the voyage from the Cape of Good Hope to Texel would have provided no empirical basis for preferring rotation alone to a correction based on Newton's theory, or even one based on Richer's measurement. Huygens would still have had no compelling reason, in the absence of further evidence, that would have forced him to accept Richer's or Newton's value over his own. But equally he would have had no compelling empirical reasons to reject Richer's or Newton's value.

Conclusion

Given the information Huygens did have, he had a clear basis for making the claims he put forward in the first paragraph of the ‘Addition’ to the Discourse. We should not hold him responsible for the failure to obtain measurements of the length of the seconds-pendulum during the course of the voyage of the ship Alcmaer. One can only conjecture about the conclusions he would have drawn had he received such measurements. On the one hand, he would have been faced with evidence from the corrected course, and, on the other, evidence from the measurements of the seconds-pendulum, which, if accurate, would have come close to corroborating Richer's measurement. Maybe Huygens would have discounted the changes in the length of the seconds-pendulum as too small to be reliable, or maybe he would have begun to question Tachard's measurement of the longitude of the Cape of Good Hope. As matters stood, the evidence he had did not present him with any such problem. He will not be the last great scientist to be misled by limited data.32.


Vorige Volgende

Over dit hoofdstuk/artikel

auteurs