Tabu. Jaargang 16

[p. 111]

Partitieven, enkele syntactische en semantische aspecten^*
Emmy Jacobs

0. Inleiding

In dit artikel wil ik enkele semantische en syntactische aspecten belichten van partitieve constructies. Voor iedere generatieve taalkundige zijn de opvattingen van Selkirk (1977) en Jackendoff (1977) over de structuur van partitieven bekend. Nederlandse linguïstisten kunnen zich zeker nog de discussie tussen Klein, Wiers en Bennis herinneren, welke speelde in de jaren 1977 en 1978. In de eerste paragraaf besteéd ik dan ook uitgebreid aandacht aan syntactische analyses van bovengenoemde generatieve taalkundigen.

In paragraaf twee stel ik een analyse voor vanuit de categoriale grammatica, die aansluit op de semantiek. In paragraaf drie leg ik de theorie van de gegeneraliseerde kwantoren uit, als ontwikkeld door Barwise and Cooper en Zwarts, en geef ik een verdeling van kwantoren op grond van hun semantische eigenschappen. De Partitive Constraint kan dan als theorema van de semantiek worden afgeleid. Daarna geef ik een semantische analyse van Nederlandse partitieven. In paragraaf vier laat ik zien wat de semantische functie is van van en toon ik aan dat de determinator de semantische eigenschappen van de hele woordgroep bepaalt. In deze paragraaf geef ik tevens een verklaring voor de ongrammaticaliteit van sommige tautologieën. Vervolgens belicht ik enkele semantische problemen van woordgroepen als van drie leuke jongens. Verder komen aan bod superlatieven in partitieve constructies, zoals de laatste van de docenten en woordgroepen van de vorm NP van NP. Tenslotte geef ik een korte samenvatting van het artikel.

* Dit artikel is een herziene versie van een scriptie. Veel dank ben ik verschuldigd aan Frans Zwarts voor zijn begeleiding en waardevolle adviezen en zijn commentaar op vorige versies. Ik wil hier ook mijn dank uitspreken aan Henk Verkuyl.

1. Syntactische analyses van partitieven

1.1. Selkirk

Een partitieve constructie wordt vaak geanalyseerd als een NP binnen een NP. Niet iedere NP binnen een NP is echter een partitieve constructie. Volgens Selkirk (1977) zijn NP's van het type det-N of det-N syntactisch ambigu. (1a) geeft de structuur van een NP-complement constructie; (1b) van een partitieve constructie.

[p. 112]

(1)a	[ a[ [bunch[ of these flowers]]]]
	NP N' ‘N’ PP
b	[ [ [a bunch (of)][ [these][flowers]]]
	NP N" NP N' det N

De kern van de structuur is van belang voor het onderscheid tussen de twee constructies. Selkirk noemt de kern van een syntactische notie, die zij als volgt definieert: de kern is de eerste N van een NP die wordt gedomineerd door N' en N'', beide gedomineerd door NP en niet gedomineerd door een categorie PP, VP of AP die wordt gedomineerd door een NP.

In (1a) is flowers kern en bunch een maat die de omvang van these flowers aangeeft. In (1b) is bunch de kern van de woordgroep en bunch wordt nader gekarakteriseerd door of these flowers. Of we te maken hebben met een NP-complement-constructie of met een partitieve constructie wordt duidelijk als de woordgroep in een zin wordt gebruikt. Volgens Selkirk is er nl. congruentie vereist tussen de kern van de NP en de VP (Selkirk 1977)(2a,b).

(2)	a	a bunch of these flowers were given (NP-complement constructie)
	b	a bunch of these flowers was given (partitieve constructie)

Selkirk geeft geen duidelijke structuur voor een partitieve constructie met een numeralis. Ze suggereert een structuur volgens Ross (1976), nl. (3), welke structuur volgens haar het best de eigenschappen beschrijft.

(3)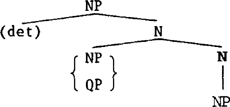

Volgens Selkirks definitie van kern, zou in de NP een van de studenten, studenten kern zijn. In dat geval is er geen sprake meer van congruentie tussen kern en specificator, evenmin overigens tussen kern en VP (4).^1.

(4)	Een van de studenten gaat/ * gaan naar Spanje.

1. Volgens Selkirk blz. 289/290 is de conditie op congruentie tussen kern en specificator niet toepasbaar op partitieve constructies van de vorm det of det N.

[p. 113]

Welke status aan of moet worden toegekend is niet duidelijk.

Om partitieve constructies als many of some apples uit te sluiten formuleert Selkerk de Partitive Constraint (5).

(5)	Rule out as ungrammatical any partitive constructions containing some, all, no, Δ = (indef) and so on in the lower NP. (Selkirk 1977, 304).

1.2. Jackendoff

Jackendoff (1977) neemt deze Partitive Constraint in iets gewijzigde vorm over. Hij merkt op, dat deze beperking refereert aan semantische functies en niet aan syntactische posities en daarom deel is van de semantische component. Kern van de partitief is volgens Jackendoff PRO (6).

(6)	[ [three] [ [PRO (of) [the men]]]]
	N" Q'" N' N N'"

Of the men is volgens Jackendoff geen PP, daar of een geïnserteerd grammatisch formatief is.

1.3. De Nederlandse linguïsten Bennis, Klein, Wiers

Ook in de discussie tussen Bennis, Klein en Wiers is de voornaamste vraag wat de kern van de constructie is.

Volgens Klein is boten kern van (7).

(7)	[ [een] [van] [de] [ [boten] [ [van] [Piet]]]]
	NP Q P det N' N PP P NP

Klein voorspelt met deze structuur correct, dat recursie van partitieve woordgroepen niet mogelijk is (8).^2.

(8)	* Een van de drie van de jongens.

Wiers echter neemt aan, dat de kern van de constructie fonologisch leeg is, zodat de structuur hetzelfde is als van een NP-complementconstructie als een auto van de vriend van mijn dochters (9) en (10).

2. Kleins structuur voorspelt echter niet, zoals Hoeksema (1983) opmerkt, dat een beperkte recursiviteit mogelijk is in b.v. ‘Een van de laatste van de aanhangers van Neeman’.

[p. 114]

(9)	[ [ ][ [een] [ [ ] [ [van] [de boten van Piet]]]]
	NP det N" QP N' N PP P NP
(10)	[ [ [een][ [auto][ [van[de vriend van mijn dochters]]]]]
	NP N'' det N' N PP P NP

Globaal genomen kan met de bezwaren die de drie linguïsten tegen elkaars analyses hebben verdelen in twee categorieën.

(A)	Argumenten gebaseerd op de interne structuur van partitieven.
(B)	Argumenten gebaseerd op zaken die buiten interne structuur vallen.

De bezwaren die Wiers heeft tegen de door Klein voorgestelde structuur vallen onder categorie A (11).

(11)	a	Er is geen congruentie tussen subject en werkwoord als boten kern is.
	b	Het reflexivum in een NP een van ons is zich en niet ons, wat je zou verwachten als ons de kern is (een van ons herinnerde zich/ *ons).
	c	In subjectpositie krijgt de hele NP een van ons het feature (+nom.); de kern zou dan zeker ook (+ nom.) moeten zijn en zou dan worden * een van wij.
	d	Het hoofd congrueert qua getal met zijn specificator. Volgens Kleins analyse zou de partitief constructie een uitzondering zijn.
	e	Indien er wordt toegevoegd in een zin met een partitieve constructie wordt de grammaticaliteit behouden (ik heb er een gezien van de boten).

Naast de bezwaren van Wiers, welke Bennis deelt, heeft Bennis er nog twee van categorie B.

f	Kleins structuur is in tegenspraak met elke versie van de X'-theorie die zegt dat ieder hoofd van een categorie gedomineerd moet worden door zijn maximale projectie.
g	Klein moet aannemen dat, gegeven de grammaticaliteit van ik heb er een gezien van de boten van Piet de PP van de boten van Piet

[p. 115]

een losse basisgegenereerde PP is, ondanks het feit, dat we hier een constructie met een partitieve PP hebben.

Als de kern van de constructie een fonologisch leeg element is, wordt Wiers geconfronteerd met een schending van de subjacentieconditie (12).

(12) Verplaats α mag slechts een boundingscategorie kruisen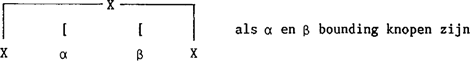

Wiers denkt aan de overtreding van de subjacentieconditie tegemoet te komen door een semantische herinterpretatie, waardoor kern en bepaling worden opgevat als een eenheid, dus [een van de boten], en de bepaling [van Piet] bij de bepaling [van de boten] wordt opgevat als een bepaling bij de eenheid [een van de boten].

Tegen deze oplossing heeft Bennis de volgende bezwaren. (13)

(13)	a	Syntactische verschillen worden dan verklaard aan de hand van een ondoorzichtig semantisch principe.
	b	Subjacentie zou niet langer een conditie op verplaatsingsregels zijn, maar een semantisch filter, dat controleert of er tussen het verplaatste element een spoor een correcte relatie bestaat.

Bennis stelt een andere analyse voor. Hij neemt ook aan dat de kern van de NP fonologisch leeg is, maar stelt voor gebruik te maken van de mogelijkheden die de X'-theorie biedt, nl. het aanhechten van constituenten op verschillende niveaus. PP's en ook S′n in een partitieve constructie moeten worden aangehecht op dat niveau dat in overeenstemming is met de interpretatie en verplaatsingsmogelijkheden, zodat we niet in problemen komen met subjacentie. In de NP een van de boten van Piet zou de PP van Piet niet een PP bij de boten zijn maar een zusterconstituent van de PP van de boten zijn (14).

(14)	[ [een][ [ []][van de boten] [van Piet]]]
	N'"/QP N" N' P'" P'"

[p. 116]

In dat geval zou bij extractie van de PP van Piet geen schending van de subjacentieconditie optreden.

Kleins bezwaren tegen de analyses van Wiers en Bennis zijn van categorie B (15).

(15)	a	Klein vindt aanhechting op verschillende niveaus niet erg aannemelijk, gezien de door Bennis veronderstelde (on)grammaticaliteit van resp. 1. en 2., waarmee Klein het niet eens is.
		1.	* Ik heb een van de voetballers ontmoet die bij NEC spelen.
		2.	Ik heb een van de voetballers ontmoet die bij NEC speelt. Bovendien vindt hij de voorspelbaarheid van een verschil in topicalisatie niet erg sterk. Verder is hij van mening (cf. van Gestel, De Haan en Van der Toorn) dat in het Nederlands geen linkswaartse verplaatsingen van PP's uit NP's voorkomen.
	b	Indien aan een partitiefconstructie en NP-complementconstructie dezelfde structuur wordt toegekend, zou zowel 1 als 2 grammaticaal zijn.
		1.	Jan heeft een voorstelling van een opera van Mozart gezien en Piet van een opera van Gounod.
		2.	Jan heeft een van de opora's van Mozart gezien en Piet * van de opera's van Gounod.
	c	In 1. kan hen coreferentieel zijn met mijn broers, maar in 2. niet.
		1.	een vriend van hen zei, dat mijn broers niet van Gounod hielden     i       i
		2.	* een van hen zei, dat mijn broers niet van Gounod hielden     i       i
	d	Zou de structuur van 1 en 2 hetzelfde zijn, dan zou in beide zinnen dezelfde anafoor gebruikt kunnen worden.
		1.	Jan is een vriend van de grootste bewonderaar van
				i
			hem/ * zichzelf
					i		i
		2.	Jan is een van de grootste bewonderaars van * hem/zichzelf
				i						i	i

[p. 117]

Bennis en Wiers geven een oplossing door het aannemen van een fonologisch leeg element als kern. Kwesties als congruentie tussen NP en VP, congruentie tussen NP en specifier, reflexivisatie van een NP binnen een partitief en toekenning van de nominatiefcasus zijn door deze assumptie opgelost.

Ook geeft Bennis een mogelijke oplossing voor de overtreding van de subjacentieconditie. Op zich is dit een aardige oplossing. Bennis zegt echter zelf, dat dit in overeenstemming moet zijn met de interpretatiemogelijkheid. Een van de boten van Piet heeft echter dezelfde interpretatie als een van Piets boten. Volgens BenniS′ analyse zou de structuur er als volgt uitzien (16).

(16)	[ [een][ [][ [van] [Piets boten]]]]
	NP det N' N PP P NP

Wordt van Piet in een van de boten van Piet aangehecht als een zusterconstituent van van de boten dan zou er betekenisverschil moeten zijn met (16).

Bennis stelt dat er in ik heb er een gezien van de boten een kwantitatief er is. Dat ben ik met hem eens. Ik vraag me alleen af wat er eigenlijk wordt gekwantificeerd. Het kwantitatieve er bindt een leeg hoofd van een gekwantificeerde NP (17).

(17)

Laten we kwantificatie in zinnen met een NP-complement en een partitief eens vergelijken (18-19).

(18)	a	ik heb twee vrienden van de meisjes gezien
	b	ik heb er twee ø van de meisjes gezien (nl. vrienden)
	c	ik heb er twee ø gezien van de meisjes (nl. vrienden)
(19)	a	* ik heb twee van de meisjes gezien
	b	* ik heb er twee ø van de meisjes gezien (er is niet lokatief)
	c	* ik heb er twee ø gezien van de meisjes (fietsen? auto's?)
	d	* ik heb er twee ø gezien
	e	ik heb er twee ø gezien

[p. 118]

In zowel (18b) als (19b) wordt de kern gedeleerd en wordt kwantitatief er toegevoegd. In (18b) wordt vrienden gedeleerd en in (19b) een leeg element (Volgens Bennis/Wiers analyse). Paradoxaal genoeg komt er in (19b) weer een leeg element voor in de plaats. Volgens Bennis is (19b - terecht - ongrammaticaal. M.i. is (19c) eveneens ongrammaticaal, tenzij er betrekking heeft op een gedeleerde lexikale kern, waarbij van de meisjes complement is, dus b.v. ‘auto's van de meisjes’, of wanneer er lokatief is. In (19a) moet van de meisjes worden gedeleerd en er worden toegevoegd, zodat we (19e) krijgen. Het kwantitatieve er heeft dan betrekking op van de meisjes, terwijl in (18b) kwantitatief er betrekking heeft op vrienden. Van + NP vormt kennelijk een geheel en kan worden gezien als kern van de constructie. Dit wordt duidelijk wanneer we in een partitiefconstructie de (volgens Bennis/Wiers) lege kern met PP deleren. De betekenis blijft onveranderd (20) in tegenstelling tot (21) waar een lexicale kern + PP wordt gedeleerd.

(20)	a	Ik heb twee ø van de kinderen van Marian gezien.
	b	Ik heb er twee ø van Marian gezien.
(21)	a	Ik heb twee vrienden van de kinderen van Marian gezien.
	b	Ik heb er twee ø van Marian gezien.

Wordt van + NP in een NP-complementconstructie gedeleerd, dan verandert de betekenis van de zin eveneens. Voegen we er toe, dan wordt de zin ongrammaticaal (22c).

(22)	a	Ik heb twee vrienden van de meisjes van Marian gezien.
	b	Ik heb twee vrienden van Marian gezien.
	c	* Ik heb er twee vrienden van Marian gezien, (er is niet lokatief)

In een partitiefconstructie blijft de betekenis behouden. Zie daarvoor (19e).

In de structuur ‘een vriend van de meisjes’ kunnen voor de kern ‘vriend’ determinatoren worden gebruikt, die niet kunnen voorkomen de ‘lege kern’ van de partitief. Zie (23).

(23)a * beide ø van de meisjes

(23') beide vrienden van de meisjes

[p. 119]

b * alle ø van de meisjes	alle vrienden van de meisjes
d? * sommige ø van de meisjes^3.	sommige vrienden van de meisjes

Determinatoren die over het algemeen worden aangeduid als definiet kunnen niet voorkomen voor de lege kern in (23), terwijl numerals en de zogeheten indefiniete determinatoren wel kunnen voorkomen voor de ‘lege kern’ (24).

(24)	a	enkele ø van de meisjes
	b	twee ø van de meisjes
	c	hoogstens drie ø van de meisjes

Een duidelijk onderscheid tussen NP-complementconstructies en partitieve constructies is echter, dat de van NP van een partitieve constructie geheel naar voren kan worden geplaatst (25) in tegenstelling tot de van NP in een NP complenentconstructie (26).

(25)	a	ik heb twee van de jongens gezien
	b	van de jongens heb ik er twee gezien
(26)	a	ik heb een vriend van Hans gezien
	b	* van Hans heb ik een vriend gezien

Resumerend kunnen we het volgende onderscheid maken tussen partitieve constructies en NP-Complement constructies (27), waarbij we een lege kern aannemen.

(27)	a	In een partitieve constructie kan de van NP geheel naar voren worden geplaatst in tegenstelling tot de van NP in een NP-complementconstructie.
	b	In een partitieve constructie wordt het tweede deel van de conjunctie ongrammaticaal, indien de determinator en (lege) kern worden gedeleerd in tegenstelling tot een NP-complement-constructie.
	c	In een zin met partitieve constructie kan het pronomen in de hoofdzin niet coreferent zijn met een subject in de bijzin.
	d	In een zin met partitieve constructie dient een ander anafoor te worden gebruikt dan in zin met NP-complementconstructie.
	e	Indien kwantitatief er optreedt in een zin met NP-complementconstructie,

3. Deze partitieve constructie is wel grammaticaal indien de woordgroep gevolgd wordt door een relatieve bijzin, b.v. ‘sommige van de meisjes, die biologie studeren’...

[p. 120]

	waarvan de kern is gedeleerd, dan is de zin grammaticaal in tegenstelling tot een zin met partitieve constructie.
f	In een zin met een partitieve constructie blijft dezelfde betekenis behouden als (lege) kern + complement worden gedeleerd. In een met NP-complementconstructie verandert de betekenis.
g	Voor partitieve constructies kunnen geen definiete determinatoren voorkomen in tegenstelling tot zinnen met NP-complementconstructies.

De argumenten van Klein hier geciteerd onder (15b-d) en mijn eigen observaties acht ik sterk genoeg om BenniS′ analyse te verwerpen. Een partitiefconstructie kan niet dezelfde structuur hebben als een NP complementconstructie. Dit laatste impliceert niet dat ik Kleins analyse juist acht. Partitieve constructies te analyseren vanuit de X'-theorie schijnt toch moeilijkheden op te leveren. Ik wil dan ook trachten de partitieven te verklaren vanuit de semantiek, maar eerst een analyse geven volgens de categoriale grammatica, die aansluit op de semantiek.

2. Een categoriale syntaxis voor de partitiefconstructie

De syntaxis die ik wil suggereren is een eenvoudige categoriale grammatica, bestaande uit primitieve en afgeleide categorieën^4..

Afgeleide categorieën:

Als α en β categorieën zijn, dan is α/β een categorie, α en β kunnen alle mogelijke categorieën zijn, zowel primitieve als afgeleide categorieën.

Syntactische regel:

Als α een uitdrukking is van categorie X/Y en β een van categorie Y, dan is α/β een uitdrukking van categorie X.

Primitieve categorieën:

S, VP, N.

Afgeleide categorieën:

NP = S/VP TV = VP/NP det = NP/N det(i) = N/NP AP = N/N prep = N/N/NP

4. Ik neem aan, dat lezers op de hoogte zijn van categoriale grammatica. Indien dat niet het geval is, verwijs ik naar Gamut: Logika 1 en 2.

[p. 121]

De structuur van: Renee ziet een vriend van de meisjes is gegeven in (28) en Renee ziet een van de meisjes in (29).

(28)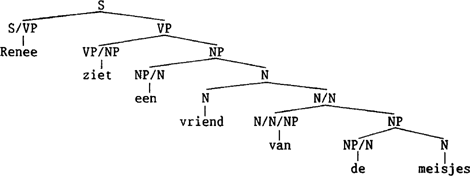

(29)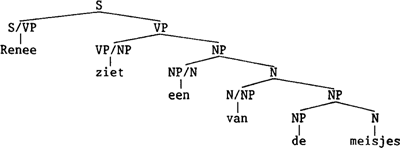

In (28) is van de meisjes het complement van het substantief vriend en het staat daarmee in een possessieve relatie. In (29) is N/NP een inverse determinator^5. die opereert op een NP om een N op te leveren, zodat daarop weer een determinator kan opereren. Van heeft hier de betekenis deel van. In (28) is dat niet het geval, daar kunnen we van een uitgespelde genitiefcasus noemen. In de partitiefconstructie is de kern van de N. De determinator bepaalt vervolgens of het substantief enkelvoud of meervoud is, zoals de determinator ook bepaalt of we al of niet met een monotone kwantor te maken hebbgen. Zier hiervoor paragraaf 4.

5. Voor zover mij bekend, werd het begrip inverse determinator voor het eerst geïntroduceerd door Zwarts in een lezing getiteld ‘Uhlenbeck revisited’.

3. Semantische aspecten van partitieven

3.1. NP's als gegeneraliseerde kwantoren'^6.

Kwantoren worden meestal opgevat als woorden of woordgroepen die een hoeveelheid uitdrukken, zoals b.v. veel, minstens drie, de meeste. Anderen en met name Barwise and Cooper - in navolging van Montaguevatten veel, de meeste etc. op als determinatoren, die tezamen met een substantief een NP opleveren, b.v. minstens drie honden, veel jongens,

6. Degenen, die bekend zijn met de theorie van de gegeneraliseerde kwantoren kunnen 3.1. en 3.2. zonder bezwaar overslaan.

[p. 122]

de meeste meisjes. De NP wordt dan in zijn geheel als kwantor gezien.

Uitdrukkingen van een taal kunnen met behulp van een predikaatlogisch model worden geïnterpreteerd. Een model M is dan een geordend paar M = <E,// //>, waar E - het discussiedomein - een niet-lege verzameling is van dingen, zoals entiteiten, individuen etc. en // // een functie, die aan de uitdrukkingen van de taal een interpretatie op het discussiedomein toekent. Twee modellen zijn verschillend, als hun discussiedomein verschillend is, of als ze verschillende functieinterpretaties hebben.

In de standaard eerste orde predikatenlogica kennen we twee kwantoren, de ∀-kwantor (universele kwantor) en de ∃-kwantor (existentiële kwantor). In de eerste orde predikatenlogika wordt gekwantificeerd over objecten in E. Kwantoren als de meeste N en meer dan de helft van N kunnen echter niet worden geïnterpreteerd als ∀-kwantor of als ∃-kwantor. In de tweede orde predikatenlogika wordt gekwantificeerd over verzamelingen van dingen. Een substantief wordt geïnterpreteerd als een deelverzameling van E. Gecombineerd met een determinator levert een substantief een NP op, die wordt geïnterpreteerd als een collectie deelveramelingen van E. Dergelijke NP's worden gegeneraliseerde kwantoren genoemd. De structuur van deze gegeneraliseerde kwantor is dan semantisch equivalent aan de structuur van de NP (30).

(30)

Dus NP's als veel jongens, de meeste vrouwen, de studenten zijn gegeneraliseerde kwantoren. De kwantor verwijst naar de collectie deelverzamelingen m.b.t. een model. De interpretatiefunctie // // voegt aan de kwantor op M een waarde 1 toe als de kwantor deel uitmaakt van de collectie deelverzamelingen van E en de waarde ø als dat niet het geval is. We kunnen ook zeggen, dat een kwantor de collectie deelverzamelingen in tweeën splitst. Een collectie deelverzamelingen levert de waarde 1 (waar) op en de andere collectie de waarde ø (onwaar). We laten de kwantor verwijzen naar de collectie verzamelingen die de waarde 1 oplevert.

Stel, dat het discussiedomein bestaat uit een verzameling {a,b,c}. vrouwen verwijst naar een deelverzameling van E {a,b} en slapen naar {a, c}.

[p. 123]

//alle vrouwen// is een collectie verzamelingen uit de machtsverzameling van E. De machtsverzameling is de verzameling van alle verzamelingen van E en is in dit model: {{0}, {a}, {b}, {c}, {ab}, {ac}, {bc}, {abc}} en wordt aangeduid door E *, //alle vrouwen// Is een collectie verzamelingen, die de verzameling //vrouwen// als deelverzameling bevat (geïllustreerd in (31)).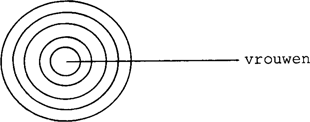

Deze deelverzameling in (31) is de kern van de generator^7. van de kwantor. Enkele vrouwen verwijst eveneens naar een collectie deelverzamelingen uit de machtsverzameling van E. //Enkele vrouwen slapen// is waar als //slapen// deel uitmaakt van het domein, waarnaar enkele vrouwen verwijst. In dit model b.v. de collectie verzamelingen {{a,b}, {a,c}, {a,b,c}. //slapen// Is de verzameling {a,c} en is een element van de collectie verzamelingen waar enkele vrouwen naar verwijst.

7. Een generator is een functie. De generator van b.v. de positief even getallen is 2. 2 wordt steeds toegevoegd aan het voorgaande getal, zodat we de reeks 2, 4, 6... krijgen. De generator van de positief natuurlijke getallen is 1. Dan ontstaat de reeks 1, 2, 3...

3.2. Enkele eigenschappen van kwantoren.

Kwantoren kunnen worden onderverdeeld in twee subklassen, niet-monotone kwantoren^8. en monotone kwantoren, terwijl de laatste weer kunnen worden verdeeld in monotoon stijgende en monotoon dalende kwantoren. Definities worden gegeven in (32) en (33).

(32)	Monotoon stijgende kwantoren Een kwantor is monotoon stijgend als op elk model M en voor alle X, Y ⊆ E geldt: als X ∈ Q en X ⊆ Y dan is Y ∈ Q.
(33)	Monotoon dalende kwantoren Een kwantor is monotoon dalend als op elk model M en voor alle X, Y ⊆ E geldt: als X ∈ Q en Y ⊆ X dan is Y ∈ Q.

Of een NP monotoon stijgend of dalend is kan op de volgende manier worden getest. We nemen een NP en twee VP's zodanig, dat de verwijzing van VP1 een deelverzameling is van de verwijzing van VP2 en we checken

8. Niet-monotone kwantoren zijn b.v. precies drie N, enkele maar niet alle N, de helft van alle N.

[p. 124]

of de volgende zinnen logisch geldig zijn (34) en (35).

(34)	Als NP VP1 dan NP VP2 (NP monotoon stijgend)
(35)	Als NP VP2 dan NP VP1 (NP monotoon dalend)

Stel VP1 is hard lopen en VP2 is lopen, dan is het zo, dat we op grond van de waarheid in de eerste zin, de gevolgtrekking in de tweede zin kunnen maken (36).

(36)	Als alle hazen hard lopen, dan lopen alle hazen.

Het omgekeerde is niet geldig, want er kunnen hazen lopen, die niet hard lopen. Alle hazen is een monotoon stijgende kwantor. Een monotoon dalende kwantor gedraagt zich tegengesteld, zoals wordt aangetoond in (37).

(37)	Als geen schildpad loopt, dan loopt geen schildpad hard.

Het omgekeerde is eveneens niet geldig.

Het is mogelijk een verdere verdeling te maken. Monotoon stijgende kwantoren kunnen een combinatie van features hebben, zoals gegeven in (38) en monotoon dalende kwantoren een combinatie van features zoals gegeven in (39).^9.

(38)	semantische eigenschappen
	van stijgende kwantoren	voorbeelden
	[+filter]	de N
	[+sterk]	beide N
	[+zuiver]
	[+filter]	alle N
	[+sterk]	elke N
	[-zuiver]
	[-filter]	sommige N
	[+sterk]
	[+zuiver]

9. Ik heb alleen de relevante eigenschappen vermeld.

[p. 125]

	[-filter]	de meeste
	[+sterk]
	[-zuiver]
	[-filter]	enkele N
	[+zwak]	veel N
	[-zuiver]	niet alleen N
(37)	semantische eigenschappen van dalende kwantoren	voorbeelden
	[+ideaal]	geen van de N
	[+sterk]	niet beide N
	[+zuiver]
	[+ideaal]	alleen N
	[+zwak]	geen N
	[-zuiver]	niemand
	[-ideaal]	niet all N
	[+sterk]
	[-zuiver]
	[-ideaal]	slechts enkele N
	[+zwak]	weinig N
	[-zuiver]

Hieronder geef ik de definities van de eigenschappen van kwantoren en - indien mogelijk - een voorbeeld om ze te checken.

(40)	filter
	Een kwantor Q ≠ ø is een filter op E dan en slechts dan als elk model M voor alle X, Y ⊆ E geldt: (X ∈ Q & Y∈Q) ↔
	X ∩ Y ∈ Q
	Voorbeelden: alle N, de N
	Alle jongens slapen en alle jongens dromen ↔
	Alle jongens slapen en dromen
(41)	Ideaal
	Een kwantor Q ≠ ø is een ideaal op E dan en slechts dan als

[p. 126]

	voor elk model M voor alle X, Y⊆E geldt: (X∈Q& Y∈Q<--->
	X ⋃ Y∈Q.
	Voorbeelden: geen van de N, geen N
	Geen meisje lacht en geen meisje danst <--->
	Geen meisje lacht of danst
(42)	Zuiver/onzuiver
	Een kwantor Q op E is zuiver dan en slechts dan als voor elk model M geldt Q ≠ ø en Q ≠ E *
	Als Q niet zuiver is, dan is Q onzuiver.
	Voorbeelden: alle N, elke N, geen N, niet alle N.
	Zoals eerder vermeld, verwijst de kwantor naar de deelverzamelingen met betrekking tot een model. Er zijn situaties - afhankelijk van het model - waarbij de kwantor verwijst naar alle deelverzamelingen van het domein - de machtsverzameling E * - of naar de lege verzameling. Indien de kwantor verwijst naar de machtsverzameling of de lege verzameling, dan is de kwantor onzuiver. Doen deze gevallen zich niet voor, dan is de kwantor zuiver.
(43)	Sterk/zwak
	Een NP is positief sterk dan en slechts dan als voor elk model M geldt: E ∈ Q.
	Een NP is negatief sterk dan en slechts dan als voor elk model M geldt: E ∉ Q.
	Als een NP niet sterk is, is deze zwak.
	Deze definitie spreekt voor zichzelf. Uit de definitie volgt, dat zuiver monotoon stijgende kwantoren altijd positief sterk zijn en zuiver monotoon dalende kwantoren altijd negatief sterk.

In (44) zijn de semantische eigenschappen van NP's in een schema gezet.

[p. 127]

(44)a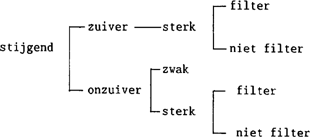

(44)b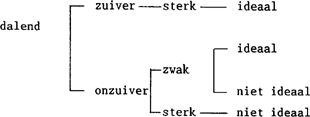

3.3. Een semantische analyse van Nederlandse partitieven

Welke kwantoren kunnen nu voorkomen in partitieve constructies? Beschouwen we de volgende voorbeelden (45).

(45)	a	een van beide vissen
	b	twee van de studenten
	c	een van de beide biologen
	d	* twee van sommige ministers
	e	* een van de meeste bussen
	f	* drie van alle kamerleden
	g	* een van enkele mannen
	h	* twee van geen vrouwen

Laten we eens kijken naar de eigenschappen van de NP's in de hierboven gegeven partitieve constructies. De NP's in (a-g) zijn stijgend en die in (a-f) zijn bovendien positief sterk. De NP's in (a-c) zijn zuivere filters en de NP in f is een onzuiver filter. Zie voor een overzicht (46).

[p. 128]

		stijgend			dalend
(46)			filtrerend	niet filtrerend
	s		beide N
	t	zuiver	de beide N	sommige N
	e		de N
	r
	k
		onzuiver	alle N	de meeste N
	z			enkele N
	w				geen N
	a
	k

Barwise and Cooper (184) stelden het volgende (47):

(47)

‘If ± is a definite NP and if Q = // // is its denotation, then ⋂ Q the intersection of all sets in Q, is the generator of Q. In the case of “the N”, we have ⋂ //the n N// = //N//. We suspect that it is this ability to uniquely determine the generator from the NP that allows the NP to play the role of a common noun and recombine with a determiner.’

De definiete determinator wordt door Barwise and Cooper als volgt gedefinieerd (mijn vertaling)(48):

(48)	Een determinator D is definiet als voor elk model M = <E, // //> en elke A waarvoor //D//(A) is gedefinieerd er een niet lege verzameling B is, zodat //D//(A) zuiver is {X ⊆ E/B ⊆ X}.

Hieruit volgt, dat in partitieve woordgroepen van de vorm [...NP] de laatste NP altijd zuiver en filtrerend moet zijn.^10.11.

De NP's voorkomend in de grammaticale constructies hebben alle de eigenschap zuiver en filtrerend. De NP's van de ongrammaticale en onwelgevormde constructies missen de eigenschap zuiver en/of filtrerend. De lezer kan dit gemakkelijk checken aan schema (46).

(47) Houdt in dat NP's in partitieve constructies dus altijd stijgend en positief sterk zijn. Dat een NP in een partitieve constructie niet dalend kan zijn ligt vor de hand. Stel je hebt een domein E met een verzameling {a,b,c} en //vrouw//= {a,b}. Geen vrouw verwijst dan

10. In het Engels zijn partitieve als ‘one of both’ ongrammaticaal. Zie voor een verklaring Ladusaw (1982).

11. De Jong en Verkuyl (1984) nemen aan, dat zuiverheid een incidenteel fenomeen is en geen classificerend element van kwantoren. Volgens hun analyse is alle zuiver en filtrerend, evenals beide en de. Ik ben het met hun opvatting niet eens. Als alle N en de N dezelfde eigenschappen hebben zouden dezelfde modifiers moeten kunnen opereren op deze kwantoren. We kunnen wel zeggen bijna alle studenten, maar niet bijna de studenten of praktisch de studenten. Zie verder ook Jacobs 1984.

[p. 129]

naar de collectie verzamelingen {{c}{ø}. Er is geen generator. Dat bij niet filtrerende NP's... van NP eveneens ongrammaticaliteit oplevert, laat zich op de volgende manier beredeneren.

Als NP een filtrerende nominale constituent is en als Q = //NP// zijn verwijzing, dan is Q - de doorsnede van alle verzamelingen in Q - de generator van Q. De NP kan opnieuw de rol van een substantief op zich nemen en weer worden gecombineerd met een determinator. In het geval van sommige N kan de generator niet uniek worden bepaald. Vandaar dat b.v. twee van sommige ministers als onwelgevormd kan worden beschouwd. Neem b.v. (49):

(49)	Sommige ministers bezuinigen en sommige ministers plaatsen kruisraketten

Dit houdt niet in, dat de ministers die bezuinigen ook kruisraketten plaatsen, want als we de eerste NP Q1 noemen en de tweede NP Q2 dan is het niet zo, dat de doorsnede van X (bezuinigen) en Y (kruisraketten plaatsen) zowel een element is van Q1 als van Q2. Het is heel goed mogelijk, dat de doorsnede van X en Y ø is, in tegenstelling tot (50).

(50)	Beide ministers bezuinigen en beide ministers plaatsen kruisraketten

waar de generator wel uniek kan worden bepaald.

Dat een NP zuiver moet zijn kan men als volgt beredeneren.^12. Een monotoon stijgende NP is zuiver als deze niet naar de machtsverzameling verwijst. Tot iedere machtsverzameling behoort ook de lege verzameling ø. Stel dat de verzameling alle kamerleden leeg is, dan levert de intersectie van alle verzamelingen in Q een lege generator op. In dat geval verwijst dus drie van alle kamerleden naar een collectie verzamelingen waarin geen kamerleden voorkomen. Aangezien uit de woordgroep drie van alle kamerleden niet is op te maken of de verzameling leeg is, is de zin ongwelgevormd. Indien echter alle kamerleden nader wordt gedefinieerd door b.v. een relatieve bijzin of indien de existentie wordt voorondersteld, dan zijn dergelijke partitieve constructies wel grammaticaal, zoals b.v. in (51), waar voorondersteld wordt, dat de collectie niet leeg is:

12. Zie hiervoor ook De Jong en Verkuyl ‘Generalized Quantifiers: The Properness of their Strength’ (32).

[p. 130]

(51)	a	slechts drie van alle kamerleden die voor de motie stemden...
	b	zestig procent van alle kamerleden is voor...
	c	de helft van alle studenten Engels is geslaagd
	d	twee derde van alle kiezers stemden voor Wubbes

In (51a) wordt kamerleden nader gedefinieerd door die voor een motie stemden. De collectie is dus niet leeg. In (51b) is er een collectie kamerleden, voorondersteld door zestig procent. In (51c) wordt door de helft al voorondersteld dat er studenten zijn die Engels studeren en ook in (51d) geeft twee derde al aan, dat er kiezers zijn.

Uit hetgeen hierboven is gesteld en uit de difinities van B&C kan de volgende stelling worden geponeerd (52):

(52)	NP's die voorkomen in de woordgroep [... van NP] van partitieve constructies dienen filtrerend te zijn en
	a.	zuiver of
	b.	hun existentie is voorondersteld

De Partitive Constraint kan nu als theorema worden afgeleid.

4. De semantische functie ‘van’

Gaan we uit van B&C's analyse, hier geciteerd onder (47), dan legt van een relatie tussen NP's en N's. Immers, de generator van een NP is een deelverzameling van alle andere verzamelingen, van Kan dan worden gezien als een functie van NP's naar N's. Definitie van een functie is gegeven in (53):

(53)	Een relatie R in A × B is een functie dan en slechts dan als
	a.	het domein van R gelijk is aan A;
	b.	elk element in het domein gepaard gaat met slechts een element in het bereik.

Voorbeeld van een functie f: A ⇢ B, gevisualiseerd in (54), waarbij A het domein is en B het bereik. Stel A = {{a,b,c}, {a,c}, {a,d} en B = {{a}, {b}}

[p. 131]

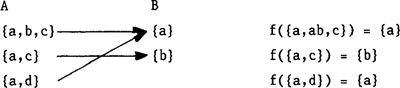Ieder element uit A wordt gepaard met een element uit B. De functie bestaat dan uit de verzameling geordende paren R = {<{a,b,c,}, {a}> <{a,c}, {b}> <{a,d}, {a}>}. De omgekeerde relatie (inverse) is vaak geen functie. De inverse van een functie f: A ⇢ B is slechts dan ook een functie indien aan de volgende voorwaarden is voldaan.

c	Niet twee verschillende elementen van A gaan gepaard met hetzelfde element van B.
d	f is onto B. Dat wil zeggen dat het bereik van de functie alle elementen van de verzameling onder B bevat.

De inverse van de functie R-1 (54) is in dit geval dus geen functie, omdat niet ieder element uit B gepaard gaat met slechts een element uit A. Deze relatie bestaat uit de geordende paren <{a}, {a,b,c,}>, <{a}, {a,d}>, <{b}, {a,c}>. {a} gaat zowel gepaard met {a,b,c,} als met {a,d}.

De functor van reduceert een NP tot een N indien de generator uniek kan worden bepaald, d.w.z. als de NP filtrerend en zuiver is zodat op de N opnieuw een determinator kan opereren. Deze determinator van de van NP woordgroep bepaalt vervolgens of de gehele kwantor monotoon is en zo ja, stijgend of dalend. Precies twee van de honden is b.v. een niet-monotone kwantor, want op grond van de waarheid in (55a) kunnen we niet de gevolgtrekking maken in (55b), noch kan (55a) uit (55b) volgen.

(55)	a	Precies twee van de honden lopen hard
	b	Precies twee van de honden lopen

Immers als precies twee van de honden hard lopen, volgt daaruit niet dat precies twee honden lopen. Dat ook het omgekeerde niet geldig is kan de lezer zelf controleren. Geen van de honden is een dalende kwantor, zoals wordt aangetoond in (56).

Ook hier bepaalt de determinator geen de monotonie van de gehele woordgroep.

[p. 132]

(56)

Geen van de honden loopt

Geen van de honden loopt hard

4.1. Tautologieën

Van is dus een functie van NP's naar N's. De determinator voor van is dan weer een functie van N's naar NP's en wordt weer geïnterpreteerd als een collectie deelverzamelingen van E. Woordgroepen als (57) zijn m.i. ongrammaticaal. In beide woordgroepen is sprake van een tautologie.

(57)	a	*?Twee van beide vrienden
	b	*?alle van de studenten

Een verklaring voor deze ongrammaticaliteit is m.i. de volgende. Stel we hebben een domein E met een verzameling {a,b,c}. Studenten verwijst naar een deelverzameling van E {a}. //de studenten// Is een deelverzameling van de machtsverzameling, nl. {{a,}, {ac}, {ab}, {abc}}. De functie is de verzameling geordende paren {<{a}, {ab}>, <{ab}, {a}>, <{ac}, {abc}>, <{abc}, {ac}>. Zie (58).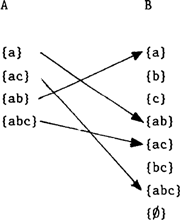

Van is weer een functie van NP's naar N's en levert b.v. weer de elementen genoemd onder A. Nu dient nog een determinator op de van NP woordgroep te opereren. Indien deze determinator alle is, krijgen we de woordgroep alle van de studenten. De functie wordt dan als volgt gevisualiseerd (59):

[p. 133]

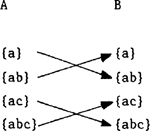De inverse van deze functie is eveneens een functie. De functie is onto, en ieder element uit B gaat weer gepaard met precies een element uit A. Het feit, dat de inverse van de functie eveneens een functie is, biedt m.i. de verklaring voor de ongrammaticaliteit van de woordgroepen in (57).^13.

13. Partitieve constructies als elk van beide studenten acht ik minder onwelgevormd dan twee van beide studenten. Een verklaring hiervoor kan ik vooralsnog niet geven.
We kunnen uitdrukkingen als deze gebruiken als antwoord op een verbaasde vraag met nadruk op beide: beide studenten??? met als definitieve bevestiging: ja, elk van beide studenten.

5. Andere (mogelijk) partitieve constructies

Behalve de in het vorige hoofdstuk behandelde partitieve constructies kent het Nederlands nog een aantal woordgroepen, die we mogelijk partitieven kunnen noemen, b.v. van die honden in ‘er lopen van die honden in de tuin’; superlatieven als ‘de muzikaalste van mijn vrienden’; woordgroepen van de vorm NP van NP als ‘een dozijn van die rozen; een groep van die mannen; een emmer van die lekkere bramen; een massa van die studenten.

Laten we deze woordgroepen eens van naderbij beschouwen.

5.1. Woordgroepen van die N

Iedere Nederlander kent woordgroepen als van die honden in: ‘er lopen van die honden in de tuin’. Dergelijke woordgroepen kunnen optreden als subject. Indien van een gewone prepositie zou zijn, dan is het vreemd dat een dergelijke woordgroep subject kan zijn. In het Nederlands zijn subjecten altijd NP's en geen PP's^14.. De betekenis van een dergelijke woordgroep kunnen we ongeveer omschrijven als sommige, maar niet alle honden. Sommige, maar niet alle N is een niet- monotone kwantor. Is van die N eveneens een niet-monotone kwantor of is deze woordgroep monotoon? In (60) volgt de b-zin uit de a-zin.

(60)	a	Er lopen van die honden hard in het park ⇢
	b	Er lopen van die honden in het park

14. Een van de reviewers van een vorige versie was het hiermee niet eens. Als voorbeeld gaf hij:

Ik heb veel essays over Vestdijk gelezen, maar ik weet niet of er ook over Hermans geschreven zijn.

In dit geval hebben we te maken met de deletie van de kern van de woordgroep. Het voorbeeld is m.i. onjuist. Dit geldt ook voor het volgende voorbeeld (van dezelfde reviewer).
De meeste mannen dragen een hoed. Maar er zijn er ook met een pet. Ook hier is sprake van deletie van de kern in de tweede zin. De tweede zin is zonder de eerste zin zonder enige betekenis.

[p. 134]

Het predikaat vertoont duidelijk stijging, maar is de stijging het gevolg van van die honden of van er? er Is nl. ook een monotoon stijgende kwantor, zoals aangetoond in (61).

(61)	Er wordt mooi gedanst ⇢ Er wordt gedanst

Als van die honden een monotone stijger is, dan moet een zin met een positief polair item, dat minimaal wordt ge-c-commandeerd vanuit de kanonieke richting door een dergelijke kwantor, grammaticaal zijn.^15..

We nemen als voorbeeld de positief polaire items verre van gelukkig, nogal, net zo goed en vergelijken (62) met (63).^16..

(62)	a	Sommige van deze mensen zijn verre van gelukkig.
	b	Enkele van de accountants voelen zich nogal aangesproken.
	c	Enkele van de studenten kunnen net zo goed de trein nemen.
(63)	a	*?Er zijn van die mensen verre van gelukkig.
	b	*?Er voelen zich van die accountants nogal aangesproken.
	c	*?Er kunnen van die studenten net zo goed de trein nemen.

Uit (63) zou men kunnen concluderen, dat van die mensen niet-monotoon of dalend is. Een dalende kwantor is echter niet mogelijk, want in een zin met twe kwantoren, waarvan er een dalend is, is het predikaat eveneens dalend.^17. Een tweede argument ten gunste van non-monotonie is gebaseerd op conjunctie. B&C stellen, dat zinnen met conjunctie van twee NP's van verschillende monotonie onacceptabel zijn. Zwarts (1981) toonde echter aan, dat conjunctie van een niet-monotone kwantor en een monotone kwantor acceptabele zinnen oplevert (64).

(64)	a	Deze student kent zes schilders en enkele dichters.
	b	Deze geleerde heeft tien kanaries en geen enkel boek.

Bekijken we nu conjunctie van een monotone kwantor en een van NP woordgroep.(65)

(65)	a	Deze vrouw kent van die schilders en alle dichters.
	b	Die vrouw nodigde van die componisten en geen enkele dichter uit.

15. Jacobs (1986) toont aan, dat zinnen met positief polaire items (PPI's) altijd grammaticaal zijn als de PPI wordt ge-c-commandeerd door een stijgende kwantor.

16. Zie voor meer PPI's: Seuren 1975.

17. Zie hiervoor eveneens Jacobs 1986.

[p. 135]

Ook deze zinnen zijn grammaticaal.

Een argument voor monotonie is echter het volgende. In een zin met twee kwantoren, waarvan de een monotoon is en de ander niet-monotoon, vertoont het predikaat geen monotonie. (Zie 66 en 67).

(66)	a	precies vijf kinderen hebben enkele kersen snel gegeten ↛
	b	precies vijf kinderen hebben enkele kersen gegeten
(67)	a	geen kind heeft precies 3 km gelopen ↛
	b	geen kind heeft precies 3 km hard gelopen^18.

Gebruiken we in plaats van precies vijf kinderen de woordgroep van die kinderen dan volgt de b-zin wel uit de a-zin. (68)

(68)	a	van die kinderen hebben enkele kersen snel gegeten ⇢
	b	van die kinderen hebben enkele kersen gegeten

Ook in (69) volgt de b-zin uit de a-zin.

(69)	a	geen kind heeft van de kersen gegeten ⇢
	b	geen kind heeft van die kersen snel gegeten

Resumerend kunnen we vaststellen dat we twee argumenten hebben tegen monotonie van de woordgroep van die N, nl. het conjunctie-argument en het argument met de positief polaire items, en een argument voor een monotonie, zoals aangetoond in (68) en (69). Nader onderzoek zal uit moeten maken of de woordgroep van die N wel of niet monotoon is.

18. Een uitzondering vormt misschien een zin met een niet-monotone en een universele kwantor, zoals:

Precies drie kinderen hebben alle kersen snel gegeten
Precies drie kinderen hebben alle kersen gegeten.

Verwijst ‘alle kersen’ naar een universeel domein, dat alle kersen bevat, dat is het predikaat stijgend. Verwijst ‘alle kersen’ daarentegen naar een beperkt domein, b.v. de kersen die per kind zijn uitgedeeld is het predikaat niet-monotoon.

5.2. Superlatieven

Volgens Jackendoff kunnen ook superlatieven voorkomen in partitieve constructies, b.v. (70):

(70)	a	John is de muzikaalste van mijn vrienden
	b	Ellen is de aardigste van mijn vriendinnen

Is er inderdaad sprake van een partitief-constructie? Laten we nog eens kijken naar de interpretatie van een substantief. Een substantief verwijst naar een deelverzameling van het discussiedomein E.

[p. 136]

//vriend// Is een verzameling van eigenschappen, waarvan een eigenschap, dus een element van de verzameling eigenschappen, muzikaliteit is. Stel we hebben een discussiedomein E met {a,b,c}. Vrienden verwijst naar {a,b} en de eigenschap muzikaal verwijst naar een element uit de verzameling, b.v.: b Mijn vrienden verwijst naar de collectie verzamelingen {{a,}, {b}, {a,b,c} {a,b}{a,c}}. Mijn muzikale vrienden verwijst naar de collectie verzamelingen {{a,b}, {a,b,c}{b}}. Een van deze muzikale vrienden is de muzikaalste en verwijst b.v. naar {a,b} en verwijst naar een deelverzameling van de collectie verzamelingen {{a}, {b}, {a,b,c}, {a,b}, {a,c}}. Ook hier hebben we meer te maken met een functie.

Gaan de punten genoemd onder (27) ook op voor deze partitieven?

In (71) kan van NP naar voren worden geplaatst.

(71)	a	John is de muzikaalste van mijn vrienden
	b	van mijn vrienden is John de muzikaalste

In (72) is de samentrekking ongrammaticaal, evenals in (15.b.2.).

(72)	Jan heeft de mooiste van de opera's van Mozart gezien en Piet
	* van de opera's van Gounod.

In (73) kan hen niet coreferentieel zijn met mijn broers, evenmin als in (15.c.2).

(73)	* de leukste van hen zie, dat mijn broers niet van Mozart
	hielden	i	i

Ook het anafoor, dat gebruikt moet worden in (74) komt overeen met het anafoor dat gebruikt moet worden in (15.d.2).

(74)	Jan is de leukste van de bewonderaars van * hem/zichzelf
	i	i	i

Deze partitieven komen overeen met partitieven als enkele van de N. het enige verschil is dat voor een superlatief altijd de determinator de of het moet worden gebruikt, i.t.t. de andere partitieven.^19..

19. Immers, een kan maar de muzikaalste zijn of de aardigste of de laatste.

[p. 137]

5.3. Woordgroepen van de vorm NP van NP.

Deze woordgroepen kunnen worden verdeeld in:

1.	Woordgroepen waarvan de eerste NP een hoeveelheid of gewicht uitdrukt, zoals een dozijn van die rozen, een kilo van die lekkere appels.
2.	Woordgroepen waarvan de eerste NP een onbepaalde telbare hoeveelheid uitdrukt, zoals een aantal van de kinderen; een paar van die auto's; een meerderheid van de kamerleden.
3.	Woordgroepen waarvan de eerste NP een onbepaalde, niet telbare maar wel in omvang beperkte hoeveelheid uitdrukt, zoals een glas van die wijn; en emmer van die lekkere bramen.
4.	Woordgroepen waarvan de eerste NP eveneens een telbare heoveelheid uitdrukt, maar welke NP conceptueel niet kan worden opgevat als een deelverzameling van de NP na van.

Hoeksema (1983) is van mening, dat woordgroepen die een determinator en een hoeveelheid bevatten, zoals een dozijn en een aantal complexe determinatoren zijn. Ik kan zijn opvatting delen en ben van mening, dat we ook in die gevallen kunnen spreken van een partitieve constructie. Bij woordgroepen als een glas van deze wijn, een lepel van die Franse mosterd, een emmer van die overheerlijke bramen etc. ligt de zaak mijns inziens echter anders. Ik kom hierop terug in 5.3.3.

5.3.1.

Woordgroepen waarvan de eerste NP een hoeveelheid uitdrukt, vertonen veel overeenkomst met partitieve constructies. Laten we b.v. eens kijken naar enkele punten genoemd onder (27).

In een partitieve constructie kan de van NP naar voren worden geplaatst (73-74).

(73)	van die rozen heb ik (er) een dozijn op de markt gekocht
(74)	van die appels kon ik een kilo weggooien omdat ze wormstekig waren

Het tweede deel van een conjunctie wordt ongrammaticaal, indien de (complexe) determinator wordt gedeleerd (75).

(75)	Jan heeft een dozijn van de artikelen van Chomsky gelezen en

[p. 138]

Frans * van de artikelen van Montague

In (76) kan hen niet coreferent zijn met meisjes.

(76)	* een half dozijn van hen zie, dat de meisjes in de stad gingen
	eten	i	i

Voor partitieve constructies kunnen geen z.g. definiete determinatoren voorkomen in tegenstelling met NP-complementconstructies (77).^20.

(77)	a	* het dozijn van de meisjes
	b	* de kilo van de appels

In bovengenoemde gevallen is van een functie van NP's. De (complexe) determinator verwijst naar een deelverzameling van de collectie verzamelingen waarnaar de NP van die rozen, van die appels, etc. verwijst.

20. Een definiete determinator kan soms wel voorkomen, nl. als er een relatieve bijzin volgt.
Het dozijn van de meisjes dat gisteren in Jan Primus zat.

5.3.2.

Ook van de determinatoren een aantal, een paar, een meerderheid is de overeenkomst met partitieve constructies groot. De van NP kan geheel naar voren worden geplaatst in tegenstelling tot de van NP is NP-complementconstructies (78)-(80).

(78)	a	een paar van die auto's staan slecht geparkeerd
	b	van die auto's staan (er) een paar slecht geparkeerd
(79)	a	een aantal van de kinderen is i.v.m. de storm thuis gebleven
	b	van de kinderen is (er) een aantal thuis gebleven
(80)	a	een meerderheid van de kamerleden stemde voor de motie
	b	van de kamerleden stemde (er) een meerderheid voor de motie

Ook in deze partitieve constructie wordt het tweede deel van de conjunctie ongrammaticaal indien de (complexe) determinator wordt gedeleerd (81)-(83).

(81)	de minister heeft de meerderheid van de tweede-kamerleden op zijn hand en * van de eerste kamer tegen zich
(82)	Gijs zag een paar van de honden in de tuin en * van de katten op het balkon
(83)	Ton heeft een aantal van de vioolconcerten van Bach bezocht en

[p. 139]

Ellen *van de vioolconcerten van Mozart

Het pronomen van de hoofdzin kan niet coreferentieel zijn met het subject in de bijzin (84).

(84)	* een aantal van hen zei, dat de kinderen naar de t.v. wilden
	kijken.	i	i

5.3.3.

De woordgroepen een glas van de wijn, een lepel van de Franse mosterd, een fles van die lekkere sherry, een emmer van die heerlijke bramen vertonen minder overeenkomst met partitieve constructies. Een glas, een lepel, een fles, een emmer verwijst niet naar een deelverzameling van de collectie verzamelingen waarna de NP na van verwijst. Conceptueel is de inhoud van glas, emmer, fles etc. een deelverzameling van wijn, mosterd, bramen. We kunnen van de vervangen door met of door vol. We krijgen dan een glas met wijn, een emmer vol bramen, een lepel met mosterd etc. In echte partitieve constructies kunnen we van de niet vervangen door met. We zeggen niet ‘een paar met auto's’, ‘een aantal met kinderen’, ‘een meerderheid vol kamerleden’.

Ik zou deze woordgroepen pseudo-partitieven willen noemen. De syntaxis stemt gedeeltelijk overeen met NP-complementconstructies, gedeeltelijk met partitieve constructies.

Evenals een NP-complementconstructie kan in deze woordgroepen de van NP niet naar voren worden geplaatst.(85)

(85)	a	*van die Spaanse wijn heb ik een glas bij het eten gedronken
	b	*van die Franse mosterd heb ik een lepel bij de slasaus gedaan
	c	*van die lekkere sherry heb ik een fles in Spanje gekocht
	d	*van die lekkere bramen heb ik een emmer in de duinen geplukt

Het tweede deel van de conjunctie blijft grammaticaal bij deletie van de eerste NP (86).

(86)	a	Trudy heeft een glas van de wijn uit Griekenland gedronken en Ellen van de sherry uit Spanje
	b	Gijs heeft een lepel van de mosterd bij de slasaus gedaan en Ricky van de tomatenketchup

[p. 140]

Deze constructies komen v.w.b. de syntaxis en de semantiek overeen met NP-complementconstructies. Ik zou deze woordgroepen dan ook dezelfde structuur willen toekennen als de NP-complementconstructies.

5.3.4.

Rest ons tenslotte woordgroepen van de vorm NP van NP, waar de eerste NP eveneens een hoeveelheid uitdrukt, nl. een menigte, een massa, een groep.

Naar mijn mening kunnen we ook hier spreken over pseudo-partitieven. De van NP kan niet naar voren worden geplaatst (87)-(88).

(87)	a	een menigte van de demonstranten protesteerde tegen de sluiting van enkele vakgroepen
	b	*van de demonstranten protesteerde een menigte tegen de sluiting van enkele vakgroepen
(88)	a	een massa van de demonstranten scandeerde hatelijkheden
	b	*van de demonstranten scandeerde een massa hatelijkheden

Evenals bij een NP-complementconstructie blijft het tweede deel van de conjunctie na deletie van de determinator, grammaticaal (89).

(89)	Gerard heeft een massa van die pinda's gegeten en Geert van de borrelnootjes

Conceptueel verwijst de eerste NP niet naar een deelverzameling van de eerste collectie verzamelingen van de NP na van. Naar mijn mening schijnt de eerste NP de NP na van min of meer te bevatten.

Dat echter deze woordgroepen niet geheel gelijk zijn aan NP-complementconstructies blijkt uit het feit, dat ook nu weer het pronomen in de hoofdzin niet coreferent kan zijn met het subject in de bijzin (90).

(90)	een massa van hen zei, dat de studenten tegen de bezuinigingen
	demonstreerden	i	i

Woordgroepen als (91) dienen eveneens te worden uitgesloten als partitieve constructies. Intuïtief geven zij een vergelijk weer.

(91)	een knaap van een jongen

[p. 141]

een schat van een man

6. Besluit

In het voorgaande heb ik getracht enkele problemen met betrekking tot partitieve constructies op te lossen door middel van een semantische analyse. Dat een partitieve constructie en een NP-complementconstructie niet dezelfde structuur kan worden toegekend werd reeds door Klein aangetoond. Ook door Selkirk en Jackendoff wordt van geen prepositie genoemd, maar een grammatisch formatief. Eens te meer is duidelijk geworden, dat er tussen NP-complementconstructies grote verschillen zijn. Van is een functie van NP's naar N's, waarop een determinator kan opereren die weer een functie is van N's naar NP's. De categoriale grammatica sluit aan op deze semantische analyse.

Ook in het Nederlands kennen we pseudo-partitieven, die zowel semantisch als syntactisch onderscheiden worden van echte partitieven. Ik ben van mening, dat door de nadruk te leggen op de semantiek, een beter inzicht is verkregen in partitieve constructies. Aangetoond is, dat superlatieven kunnen voorkomen in partitieve constructies en woordgroepen, waarvan de kwantor voor van een complexe determinator is. In beide gevallen wordt door de woordgroep voor van verwezen naar een deelverzameling van de collectie verzamelingen waarnaar de NP na van verwijst.

Door van+NP te zien als een N en niet als een PP wordt ook verklaard, waarom woordgroepen als van die kanjers van vissen en van die brede straten kunnen optreden als subject, in resp. (92a-b).

(92)	a	Er zwemmen van die kanjers van vissen in de Ionische zee.
	b	Er zijn van die brede straten in Moskou.

Niet duidelijk is of deze woordgroepen moeten worden gezien als monotone of als niet-monotone kwantoren.

Ongetwijfeld zijn er nog voldoende problemen rond de partitieve constructie. Ik hoop echter dat dit artikel een bijdrage is tot beter inzicht in de problematiek.

[p. 144]

Literatuur

Barwise, J. and R. Cooper (1981) ‘Generalized Quantifiers and Natural Language’, Linguistics and Philosophy 4, 159-219.

Bennis, H. (1979). ‘Appositie en de interne structuur van de NP’. Spektator 8, 209-228.

Hoeksema, J. (1983). ‘Partitives’. ms. RU Groningen.

Jackendoff, R. (1977). X'-Syntax: A study Phrase Structure. Linguistic Inquiry Monographs, Cambridge, Massachusetts.

Jacobs, E. (1984). ‘Modifiers and Quantifiers in Dutch’. Linguistics in the Netherlands 1984. H. Bennis and W.U.S. van Lessen Kloeke.

Jacobs, E. (1986). ‘Polarity sensitivity and Generalized Quantifiers’. Linguistics in the Netherlands, Beukema en Hulk.

Klein, M. (1979) ‘De interne structuur van partitieve constructies’. Spektator 10, 295-309.

Ladusaw, W.A. (1982). ‘Semantic Constraints of the English Partitive Constructions’. Proceedings of the first West-Coast conference on Formal Linguistics.

Selkirk, E. (1977). ‘Some Remarks on Noun Phrase Structure’. Formal Syntax. Culicover, P., Wasow, T. and Akamajian, A. Academic Press, New York, 285-316.

Seuren, P.A.M. (1976). ‘Echo, een studie in negatie. Lijnen van taaltheoretisch onderzoek, p. 160;184. G. Koefoed en A. Evers.

Zwarts, F. (1981). ‘Negatief Polaire Uitdrukkingen I’, GLOT 4, 35-131.