Septentrion. Jaargang 19
(1990)– [tijdschrift] Septentrion–
[pagina 30]
| |

M.C. Escher (1898-1972) (Photo M.C. Escher heirs / Cordon Art).
| |
[pagina 31]
| |
Sciences, maths et art:
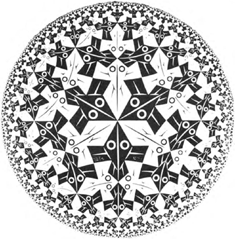
Les collègues artistes ne le comprenaient guère: trop sec, trop intellectualiste, tel était le jugement général. Le graphiste néerlandais M.C. Escher (1898-1972)Ga naar eind(1), quant à lui, se sentait plus à son aise dans la compagnie de mathématiciens et de scientifiques, tout en reconnaissant son manque de formation dans les matières concernées. Des trois côtés on était d'ailleurs à la fois ravi et étonné de se trouver ensemble. Les mathématiciens, eux, admiraient les visualisations de l'idée de l'infini qu'Escher a réalisées, surtout dans les Limites circulaires. On y voit en effet la réduction en taille de la silhouette d'un animal donnée, selon un processus en principe sans fin: la surface de travail, elle-même limitée et de forme le plus souvent circulaire mais parfois carrée, contient la silhouette donnée ainsi qu'une infinité de reproductions de cette dernière, toujours plus petites. Les scientifiques, de leur côté, jouissaient de la maîtrise des lois de la symétrie dont témoignent les oeuvres d'Escher, tout spécialement les prétendus
Remplissages périodiques de plans. Les cristallographes, par exemple, étaient stupéfaits de trouver chez Escher, non seulement les éléments de symétrie déjà connus de longue date, mais encore de nouvelles formes de symétrie, dont l'intérêt scientifique ne tardait pas à se révéler. Les cristallographes ont généreusement reconnu leur dette sur ce point. C'est en effet sous les auspices de l'Union internationale de cristallographie que Mme Pr Caroline MacGillavry (Université d'Amsterdam), elle-même cristallographe de renom, a pu publier en coopération étroite avec l'artiste, son ouvrage Symmetry aspects of the periodic drawings of M.C. Escher (1965, 1976). Elle y familiarise ses lecteurs, parmi lesquels on trouve bien entendu les étudiants de cristallographie aussi bien que les érudits intéressés,
| |
[pagina 32]
| |
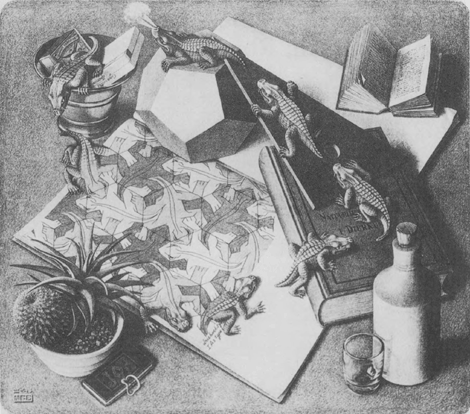
M.C. Escher, ‘Reptiles’, lithographie, 1943. On y voit incorporée une version du célèbre remplissage périodique de plan connu sous le même nom (Photo M.C. Escher heirs / Cordon Art).
années 1612-1620 dans le ‘no man's land’ qui séparait la médecine, la physique et la chimie. Qui était ce Beeckman, cet ami de Descartes (à partir de 1618), correspondant du R.P. Mersenne (1629-1633), collègue respecté de Gassendi (1629) et de Desargues (1636)? Au siècle dernier, on ne disposait guère de documentation satisfaisante. On ne connaissait Beeckman qu'à travers la correspondance de Descartes et de Mersenne. On savait donc qu'il était directeur d'une École latine, disons un Lycée, à Dordrecht, l'une des principales villes des Provinces-Unies, et qu'il tenait un journal scientifique intime. Or c'est précisément le manuscrit de ce journal qui, en 1905, a été retrouvé par l'historien Cornelis de Waard (1879-1963), à l'époque même où le monde scientifique voyait la parution des Oeuvres de Descartes. Une période de coopération francohollandaise des plus étroites s'amorça. Les éditeurs de Descartes - Adam et Tannery pour les Oeuvres et, plus tard, Adam et Milhaud pour l'édition revue de la Correspondance - allèrent consulter aux Pays-Bas le manuscrit de Beeckman, que De Waard était en train de transcrire. Avant même que la publication du journal de Beeckman ne fût assurée, De Waard fut chargé de l'édition de la Correspondance du R.P. Mer- | |
[pagina 33]
| |
senne, édition qui vient d'aboutir magnifiquement grâce aux soins de M. et Mme Armand Beaulieu. Entre 1939 et 1953 parut enfin le Journal tenu par Isaac Beeckman [...], en quatre volumes monumentaux, sous la rédaction de De Waard; en France, Pintard et Rochot avaient bien voulu le décharger partiellement de ses travaux sur Mersenne. Rien n'illustre mieux l'atmosphère de convivialité entre Paris et Amsterdam que l'édition parallèle des Oeuvres complètes de Christiaan Huygens, symbole s'il en est des bonnes relations entre les deux Académies des sciences. D'une première lecture du Journal [...] il apparut que Beeckman peut être crédité de plusieurs trouvailles scientifiques, dont l'un des premiers énoncés de la loi de la chute libre des corps développée en coopération avec Descartes (1618). Ces dernières années, il est apparu que Beeckman a aussi connu une notion bien précise de ce que nous autres modernes aurions appelé la structure moléculaire de la matière. Comme nous le verrons ci-après, celle-ci est des plus remarquables. En effet, Beeckman conçut la matière tridimensionnelle qui nous entoure comme un agrégat de particules, qu'il s'imagina à l'exemple d'êtres vivants; il les appella homogenea physiques. Ainsi, comme ces êtres vivants, les homogenea d'une substance consisteraient en un certain nombre de parties arrangées d'une certaine manière dans l'espace. A ces ‘parties’ correspondent, chez Beeckman, les atomes, dont il distingua un quartet d'espèces. Pour ne pas nous perdre ici dans les détails physico-chimiques, nous nous contenterons de dire que le savant zélandais prévit même le phénomène d'isomérie, l'une des notions-clef de la chimie moderne. Dans la réflexion des philosophes de tous les temps, de l'Antiquité à la Renaissance, le problème de la constitution de la matière phénoménale n'était d'ailleurs pas davantage qu'une partie d'une doctrine plus générale, qui incluait les problèmes du temps et du mouvement et ceux de la ligne, de la surface et de l'espace. Tous ces problèmes s'articulent en effet sur une seule et même question, à savoir: les notions concernées ont-elles trait à des entités continues ou discontinues? En d'autres termes:
Les célèbres ‘Reptiles’ d'Escher dans une interprétation d'ordinateur: R. Farinato, L. Loreto et M. Tonetti, Étude de l'ornementation du plan, programme interactif pour l'analyse du groupe cristallographique du plan, Rome, 1987.
ces entités peut-on les diviser à volonté à l'infini, oui ou non? Dans cette perspective il n'est assurément pas étonnant de voir se développer au xviie siècle, parallèlement à l'essor de la théorie moléculaire, le calcul au moyen des indivisibles, entités préfigurant les infinitésimaux du calcul différentiel et intégral. Chez Gilles Personne de Roberval (1602-1675), on voit, par exemple, l'idée qu'une surface peut être conçue comme un enchaînement de petites superficies individuelles susceptibles de servir de base au calcul de l'aire concernée. C'est ainsi qu'il crut nécessaire d'admettre qu'une ligne consiste en unités linéaires et un espace en unités spatiales. Nous voici revenus à notre point de départ: l'artiste graphique Escher. Après tout, la surface plane, pour lui, était un enchaînement d'unités planes individuelles, tout comme chez Roberval. Quelle remarquable perspective, cette gracieuse convergence de l'art, des mathématiques et des sciences! H.H. KUBBINGA
Chargé de recherches à la ‘Rijksuniversiteit Groningen’ et à l'École pratique des hautes études de Paris. Adresse: Aquamarijnstraat 12, NL-9743 RA Groningen. |
|