De Gids. Jaargang 142

[p. 279]

A.J. Kox en P.H. Polak
Christiaan Huygens (1629-1695)⁺

Driehonderd vijftig jaar geleden werd Christiaan Huygens in Den Haag geboren. Deze gebeurtenis wordt dit jaar op verschillende manieren herdacht. Maar niet op grote schaal, want Huygens is bij het grote publiek tamelijk onbekend: Bij het horen van de naam Huygens zullen de meeste mensen eerder denken aan Christiaans vader, Constantijn Huygens, de dichter-staatsman naar wie zelfs een poëzieprijs is genoemd, dan aan Christiaan zelf. Misschien zal men zich hem herinneren als de uitvinder van het slingeruurwerk. Maar hij heeft veel meer gepresteerd. We kunnen zonder overdrijven zeggen dat Christiaan Huygens een van de grootste geleerden was die ons land ooit heeft voortgebracht. Hij speelde een vooraanstaande rol in de ontwikkeling van de natuurwetenschappen, en hij was op dit gebied geruime tijd de meest vooraanstaande geleerde van de zeventiende eeuw. Zijn bijdragen waren minstens zo belangrijk als die van bij voorbeeld Galilei, Descartes en Newton. Waarom is hij dan toch tegenwoordig zo onbekend, zeker vergeleken met deze beroemdheden? Deze vraag is niet gemakkelijk te beantwoorden, maar het is wel mogelijk enkele omstandigheden te noemen die tot deze onbekendheid hebben bijgedragen.

In de eerste plaats is veel van Huygens' werk voor de lezer tamelijk ontoegankelijk door de zeer omslachtige wiskundige technieken die erin worden gebruikt. Deze technieken, die een puur meetkundig karakter hebben, gaan terug tot Archimedes, en hadden in Huygens' tijd, mede door diens toedoen, de grenzen van hun toepassingsmogelijkheden vrijwel bereikt. Vooral het beschrijven van veranderlijke grootheden, zoals bij voorbeeld de snelheid van een slinger, leverde bijna onoverkomelijke moeilijkheden op. Deze situatie veranderde toen, in het laatste kwart van de zeventiende eeuw, door Newton en Leibniz de differentiaal- en integraalrekening werd ontwikkeld. De wiskunde werd plotseling een veel machtiger hulpmiddel bij de beschrijving van de natuur. Veel resultaten die Huygens moeizaam had bereikt konden toen korter, eenvoudiger, en dus leesbaarder worden afgeleid. Hoewel hij de nieuwe ontwikkelingen wel volgde, heeft Huygens de differentiaal- en integraalrekening nauwelijks toegepast, deels uit conservatisme, deels uit een zekere minachting voor de tot bijna machinale toepassing leidende eenvoud ervan.

Een tweede omstandigheid die heeft bijgedragen tot Huygens onbekendheid is zijn terughoudendheid bij het publiceren van zijn werk. Hij stelde zeer hoge eisen aan de vorm waarin hij zijn resultaten presenteerde, en wilde niet tot publikatie overgaan voordat hij zijn bewijzen een voor hem bevredigende vorm had gegeven. Vaak ontbrak hem de tijd of de zin daartoe. Bovendien vond hij zijn resultaten soms niet belangrijk of interessant genoeg om te publiceren.

+ A.J. KOX. Promoveerde in 1976 op een theoretisch-natuurkundig onderwerp. Thans verzorgt hij de uitgave van de wetenschappelijke correspondentie van de Nederlandse natuurkundige H.A. Lorentz (1853-1928).
P.H. POLAK. Promoveerde in 1973 op een onderwerp uit de theoretische natuurkunde. Tegenwoordig is hij werkzaam bij de Stichting Wetenschappelijk Onderzoek Verkeersveiligheid SWOV te Voorburg.

[p. 280]

Van een van zijn jeugdwerken vond hij later zelfs dat het maar verbrand moest worden!^1. Het gevolg was dat veel van zijn werk pas lang na het ontstaan ervan is gepubliceerd, in een groot aantal gevallen zelfs pas na zijn dood, in de Opuscula Posthuma (1703) of in de Oeuvres Complètes (1888-1950). Vooral in de laatstgenoemde uitgave is een zeer grote hoeveelheid nog onbekend materiaal opgenomen. Veel daarvan is te vinden in Huygens' correspondentie, die 10 van de in totaal 22 delen van dit verzameld werk beslaat. Het uitgeven van de Oeuvres heeft weliswaar geleid tot een opleving van de belangstelling voor Huygens, maar toch krijgt hij nog niet de aandacht die hij verdient.

Voordat we in de rest van dit artikel uitgebreider ingaan op het leven en het werk van Huygens, wijdden we nog enkele woorden aan zijn zeer interessante opvattingen over wetenschapsbeoefening en over de rol van theorieën in de wetenschap.

In de zeventiende eeuw stonden twee opvattingen over de manier waarop de natuurwetenschap moest worden bedreven tegenover elkaar: het rationalisme en het empirisme. Volgens de aanhangers van het empirisme was alleen door middel van de ervaring verworven kennis betrouwbaar. Vooraanstaande empiristen, zoals Galilei en Bacon, streefden ernaar zoveel mogelijk ervaringskennis te verzamelen. Voor de rationalisten daarentegen was de rede de bron van alle kennis, en was empirische kennis onbetrouwbaar. De belangrijkste vertegenwoordiger van deze stroming, de Franse wiskundige en filosoof René Descartes, propageerde het denkbeeld dat de natuurkunde op dezelfde wijze moest worden opgebouwd als de wiskunde. Dat wil zeggen als een axiomatisch-deductief systeem, gegrondvest op enkele axioma's. Deze axioma's komen voort uit de rede en zijn dus in feite metafysisch van aard. Een voorbeeld is Descartes' opvatting dat de eigenschappen van stoffelijke lichamen geheel worden bepaald door hun meetkundige vorm en hun bewegingstoestand.

Huygens nam een tussenpositie in tussen empirisme en rationalisme, zoals de meeste wetenschapsmensen tegenwoordig ook doen. In een van zijn brieven gebruikt hij het motto^2. Experientia ac ratione (door ervaring en rede). Hij was van mening dat de wetenschap zich moest baseren op empirische kennis en niet op uit de rede voortkomende axioma's Maar hij zag ook in dat deze kennis zonder theoretisch raamwerk weinig waarde heeft. Daarnaast meende hij dat het experiment in laatste instantie moest beslissen over de houdbaarheid van een theorie, zonder overigens de juistheid ervan definitief te kunnen aantonen. Als illustratie van Huygens' opvattingen geven we twee citaten, beide uit een brief van 1673 aan Pierre Perrault.^3. In het eerste komt de experimentele basis van de theorie ter sprake:

‘Qu'en matiere de physique il n'y a pas de demonstrations certaines, et qu'on ne peut scavoir les causes que par les effects en faisant des suppositions fondees sur quelques experiences ou phenomenes connus, en essayant ensuite si d'autres effects s'accordent avec ces mesmes suppositions.’

Het tweede citaat belicht de rol die het experiment speelt bij het bevestigen van een theorie:

‘Mais d'autant plus qu'on trouvera de phenomenes conformes a l'hypothese, d'autant plus vraisemblable la doit on tenir. Se souvenant pourtant tousjours qu'on n'a point de demonstration de sa verite, et qu'il peut s'offrir tel autre phenomene qui estant incompatible avec nostre suppose principe le detruise absolument.’

De opvatting die Huygens in het tweede citaat onder woorden brengt, zou pas in onze eeuw algemeen aanvaard worden, mede door toedoen van filosofen als Schlick, Carnap en Popper.

Over de plaats van het experiment in de natuurwetenschappen verschilde Huygens dus van mening met Descartes. Maar op een ander, zeer belangrijk punt waren ze het eens. Evenals Descartes meende Huygens dat alle natuurverschijnselen met behulp van de mechanica moesten - en konden - worden verklaard. Van dit mechanis-

1. Het betreft hier De iis quae liquido supernatant, dat uit 1650 dateert, en is opgenomen in deel XI van de Oeuvres.

2. Oeuvres, deel III, p. 197.

3. Oeuvres, deel VII, p. 298; Pierre Perrault was de broer van Charles Perrault, de auteur van Contes de ma Mère l'Oye.

[p. 281]

tische standpunt is hij zijn hele leven niet meer afgeweken. In het Traité de la Lumière, dat in 1690 verscheen (vijf jaar voor zijn dood), heeft hij het over^4. ‘la vraye Philosophie, dans laquelle on conçoit la cause de tous les effects naturels par des raisons de mechanique’. En hij vervolgt met: ‘Ce qu'il faut faire à mon avis, ou bien renoncer à toute esperance de jamais rien comprendre dans la Physique.’ Huygens heeft zich enkele malen zeer negatief over het werk van Descartes uitgelaten^5., maar uit het bovenstaande blijkt duidelijk dat hij zich nooit geheel van hem heeft losgemaakt.

Christiaan Huygens werd geboren op 14 april 1629. Hij kwam uit een vooraanstaande familie. Zijn vader Constantijn, Heer van Zuylichem, Zeelhem en Monnikenland, was een belangrijk man in de Republiek der Verenigde Nederlanden van de zeventiende eeuw. Hij was achtereenvolgens secretaris van Frederik Hendrik en van Willem II, in navolging van zijn vader, die secretaris was van Willem van Oranje. Uit hoofde van zijn functie was Constantijn een regelmatige gast aan de hoven van Engeland en Frankrijk. Maar hij was meer dan alleen maar diplomaat. Constantijn Huygens had ook grote bekendheid als dichter. Zijn toneelstuk Trijntje Cornelis wordt ook in onze tijd nog wel opgevoerd. Bovendien was hij een verdienstelijk amateur-geleerde. Hij had een levendige belangstelling voor de natuurwetenschappen, en onderhield contacten met veel beroemde wetenschapsmensen. Eén van hen was Descartes, die zich in 1628 in Nederland vestigde en de familie Huygens regelmatig bezocht.

Toen Christiaan acht jaar oud was, stierf zijn moeder, de Amsterdamse koopmansdochter Suzanna van Baerle. Een nicht belastte zich daarna met de verzorging van het gezin, dat vijf kinderen telde. In volgorde van leeftijd: Constantijn junior, Christiaan, Lodewijk, Susanne en Philips. Het onderwijs was in handen van gouverneurs. De kinderen werden onderwezen in vakken als rekenen, muziek, Latijn, Grieks, Frans, Italiaans en zelfs logica, maar ook in dansen en paardrijden. Christiaan blonk in alles uit. Toen hij negen jaar oud was converseerde hij in het Latijn. Binnen drie jaar leerde hij de viola da gamba, de luit en het clavecimbel bespelen. Maar op het gebied van de wiskunde kwam zijn talent het meest tot uiting. Zijn vader schreef^6.: ‘A^o 1643. Begreep hy met een sonderlinge promptitude, al hetgeen de mechanique ofte eenigh ander deel van de Mathesis mogte aengaen.’ Christiaans belangstelling was niet uitsluitend theoretisch van aard, zoals blijkt uit het vervolg van dit citaat, waarin vermeld wordt dat hij zelf een draaibank had gemaakt, en ‘dat hy al eenigh goedt daer op begon te draeyen’. Om tegemoet te komen aan Christiaans grote belangstelling voor de wiskunde (waartoe in die tijd ook vakken als mechanica en astronomie gerekend werden) liet zijn vader hem door een zekere Stampioen extra lessen op dit gebied geven, ‘met sonderlingh succes’, zoals Constantijn schreef.^7.

In 1645 gingen de zestienjarige Christiaan en zijn één jaar oudere broer Constantijn rechten studeren aan de universiteit van Leiden, als voorbereiding op een diplomatieke loopbaan. Christiaan besteedde echter vooral aandacht aan de wiskunde. Zijn leermeester was de in die tijd beroemde wiskundige Frans van Schooten, een aanhanger van Descartes. In deze tijd raakte Huygens diep onder de indruk van Descartes' werk. Zoals we al zagen zou diens invloed zijn hele leven merkbaar blijven. Een andere belangrijke invloed kwam ook uit Frankrijk. Door toedoen van zijn vader begon Huygens een correspondentie met de Parijse geleerde Mersenne. De briefwisseling duurde niet lang - Mersenne stierf al in 1648 - maar was voor de jonge Huygens van groot belang. Mersenne was uitstekend op de hoogte van de nieuwste ontwikkelingen in de natuurwetenschappen en kon Huygens veel waardevolle adviezen geven. Hij was diep onder de indruk van het talent van Christiaan, en in een brief aan vader Constantijn vergelijkt hij hem zelfs met Archimedes. Misschien vormde die vergelijking voor Constantijn wel de aanleiding

4. Oeuvres, deel XIX, p. 461.

5. Oeuvres, deel X, pp. 403, 405.

6. Oeuvres, deel XXII, p. 402.

7. Zie noot 6.

[p. 282]

om zijn zoon ‘mon Archimède’ te noemen!

In 1647 verwisselde Christiaan de Leidse universiteit voor het pas opgerichte Collegium Arausiacum (Oranje-College) te Breda, waarvan zijn vader curator was. Dit college, dat door Frederik Hendrik was gesticht, had een zeer goede reputatie, maar heeft desondanks niet veel langer dan twintig jaar bestaan. Het was de bedoeling dat Huygens in Breda de rechtenstudie zou voortzetten, ditmaal in gezelschap van zijn jongere broer Lodewijk, maar evenals in Leiden kwam de wiskunde op de eerste plaats. Geen van beide broers heeft de studie afgemaakt. In 1650 werden ze door hun vader naar huis teruggeroepen, naar aanleiding van een duel tussen Lodewijk en een medestudent. Noch in Leiden, noch in Breda heeft Christiaan ooit een academisch examen afgelegd. Toch kreeg hij een titel: in 1655 kochten hij en Lodewijk een doctoraat in de rechten in het Franse Angers. Zoiets was in die tijd niet ongebruikelijk. Overigens heeft Christiaan de titel nooit gevoerd.

Huygens' eerste publikatie verscheen in 1651, onder de titel Theoremata de Quadratura Hyperboles, Ellipsis et Circuli. Het werk is gewijd aan de kwadratuur van kegelsneden, en bevat bovendien een weerlegging van een cirkelkwadratuur afkomstig van de wiskundige Gregorius a Sancto Vincentio. Al in Breda was Huygens met het werk voor deze publikatie begonnen. Drie jaar later verscheen De Circuli Magnitudine Inventa. Met dit werk over de kwadratuur van de cirkel vestigde hij zijn reputatie als wiskundige definitief. Inmiddels had Huygens besloten zich geheel aan de wetenschap te wijden, voorlopig als ambteloos burger, slechts gesteund door een jaargeld van zijn vader. De enige diplomatieke activiteit die hij ooit heeft ondernomen was een gezantschapsreis naar Denemarken in 1649. Op deze reis begeleidde hij graaf Hendrik van Nassau als diens secretaris. De voornaamste reden voor het aanvaarden van die functie was overigens de hoop geweest dat hij Descartes zou kunnen ontmoeten, die sinds kort in Stockholm woonde, waar hij hoffilosoof was van koningin Christina. Huygens’ wens ging niet in vervulling. Ook daarna zou het niet meer tot een ontmoeting komen: Descartes stierf in 1650. Hoewel het waarschijnlijk is dat Descartes de jonge Huygens bij een van zijn bezoeken aan Hofwijck wel eens gezien zal hebben, weten we vrijwel zeker dat ze elkaar nooit echt hebben ontmoet.

In de vijftiger jaren van de zeventiende eeuw raakte Huygens meer en meer geïnteresseerd in natuurkundige problemen. De zuivere wiskunde gaf hem geen voldoende bevrediging meer. Zo verdiepte hij zich in de wetten die het gedrag van botsende lichamen beschrijven, en op zeer originele wijze wist hij een aantal belangrijke resultaten af te leiden. Hoewel hij deze resultaten in 1656 in een manuscript vastlegde, en sommige ervan bekendmaakte - bij voorbeeld tijdens een zitting van de Londense Royal Society - kwam het pas na zijn dood tot volledige publikatie. Het manuscript verscheen in de Opuscula Posthuma, met als titel De Motu Corporum ex Percussione.

In Huygens' tijd was het inzicht in botsingsverschijnselen gering en verward. Descartes had in 1647 zeven regels opgesteld voor botsingen tussen twee volkomen veerkrachtige lichamen, maar op deze regels was veel aan te merken. In de eerste plaats waren er gevallen denkbaar die niet door deze regels konden worden beschreven. Bovendien waren sommige van de regels zeer duidelijk in tegenspraak met de ervaring. In feite was er slechts één juist, zoals Huygens zou aantonen. Het was de regel die het geval beschrijft waarbij twee deeltjes met gelijke massa's elkaar met gelijke snelheden langs een rechte lijn naderen, en elkaar vervolgens precies in het midden raken (‘centraal botsen’). Descartes' regel voorspelt dat de deeltjes zich na de botsing van elkaar zullen verwijderen, met snelheden die even groot zijn als voor de botsing, maar tegengesteld in richting. Evenals Descartes beperkte Huygens zich tot centrale botsingen. Verder ging hij uit van de juistheid van de zojuist genoemde regel. Maar hij had een geniaal inzicht dat bij

[p. 283]

Figuur 1: de titelpagina van De Motu Corporum ex Percussione (Oeuvres Complètes, deel XVI).

Descartes ontbrak. Hij stelde als axioma dat beweging een relatief begrip is. Daarmee bedoelde hij dat het zinloos is om over de beweging van een lichaam te spreken zonder te specificeren ten opzichte waarvan die beweging plaatsvindt. Toegepast op botsingsverschijnselen betekent dit dat alleen de snelheid van de botsende lichamen ten opzichte van elkaar (hun relatieve snelheid) van belang is voor het verloop van de botsing. Krijgen beide botsende lichamen een extra gemeenschappelijke snelheid, zodat hun relatieve snelheid niet verandert, dan zal dat op de manier waarop ze botsen geen invloed hebben.

Huygens gebruikte dit principe om uit één bekende botsing het verloop van een gehele klasse van botsingen af te leiden. Hij stelde zich een man op een boot voor, die twee aan touwen opgehangen, even zware kogels tegen elkaar laat botsen, waarbij de kogels elkaar met gelijke snelheden naderen. Zo ontstaat de botsing die Descartes op juiste wijze had beschreven. Het verloop van deze botsing is dus bekend. Op de wal staat een tweede man, die waarneemt wat er gebeurt. Hij kijkt naar de kogels, en voelt bovendien hun beweging door zijn handen op die van de man aan boord te leggen (zie Figuur 1). Begonnen wordt met de botsing uit te voeren terwijl de boot stilligt. De man aan wal registreert van beide ballen de snelheden vóór de botsing (de ‘beginsnelheden’) en de snelheden ná de botsing (de ‘eindsnelheden’). Dan wordt dezelfde botsing uitgevoerd terwijl de boot in beweging is. De man aan wal ziet nu iets anders gebeuren. Bij de beginsnelheden van de kogels moet de snelheid van de boot worden opgeteld. Maar omdat beide kogels deze extra snelheid hebben gekregen, is hun relatieve beginsnelheid niet veranderd. Aan het karakter van de botsing verandert dus niets. De man aan wal kan de eindsnelheden van de kogels na de tweede botsing nu berekenen door eenvoudig de snelheid van de boot op te tellen bij de (bekende) eindsnelheden van de kogels na de eerste botsing. Uit het verloop van een bekende botsing is op deze wijze het verloop van een ‘nieuwe’ botsing afgeleid. Omdat bij verschillende bootsnelheden voor de man aan wal telkens andere ‘nieuwe’ botsingen ontstaan, is nu het verloop van een klasse van botsingen in principe bekend. Als de snelheid van de boot de beginsnelheid van één van de kogels juist compenseert, ontstaat het speciale geval waarbij deze kogel aanvankelijk in rust is.

Huygens' formulering van het principe van relativiteit van beweging is verrassend modern. Hij was de eerste die dit principe scherp onder woorden bracht, en de manier waarop hij het toepaste wordt ook tegenwoordig nog gebruikt bij de studie van botsingsverschijnselen. Huygens beperkte zich tot botsingen, en tot bewegingen die met constante rechtlijnige snelheid plaatsvinden (‘eenparig rechtlijnige bewegingen’). In de moderne natuurkunde heeft het relativiteits-principe een wijder toepassingsgebied. In wat meer technische taal zegt men tegenwoordig dat coördinatensystemen (‘waarnemers’) die met een constante rechtlijnige snelheid ten opzichte van elkaar bewegen, voor de beschrijving van alle natuurverschijnselen gelijkwaardig zijn. Deze equivalentie heet Galilei-invariantie, maar Huygens-invariantie zou een betere naam zijn.

Tot nu toe hebben we ons beperkt tot botsingen tussen deeltjes met dezelfde massa. Huygens heeft zich echter ook verdiept in het geval van ongelijke massa's. Hierbij gebruikte hij een

[p. 284]

door hem ontwikkelde generalisatie van een theorema van de Italiaanse natuurkundige Torricelli. Huygens' generalisatie komt er, in hedendaagse termen, op neer dat bij een botsing de totale kinetische energie van de botsende deeltjes niet kan toenemen. Hij slaagde erin te bewijzen dat de kinetische energie bij botsingen tussen volkomen veerkrachtige deeltjes zelfs constant blijft. Een andere zeer belangrijke botsingswet, de wet van behoud van impuls, kende hij ook, hoewel deze wet in zijn werk een ondergeschikte plaats inneemt.

Dankzij Huygens nam het inzicht in botsingsverschijnselen aanzienlijk toe. Maar het eigenlijke belang van zijn werk ligt in de manier waarop hij tot zijn resultaten kwam. Juist daarom is De Motu Corporum ex Percussione ook voor de hedendaagse lezer nog zo interessant.

Behalve in botsingsverschijnselen was Huygens ook geïnteresseerd geraakt in optica. Al in 1653 ontstond een manuscript op dit gebied: Tractatus de Refractione et Telescopiis. Een latere versie van dit werk verscheen onder de titel Dioptrica in de Opuscula Posthuma. Bij zijn optische onderzoekingen stond Huygens een praktisch doel voor ogen: het verbeteren van de bestaande telescopen. Hij beperkte zich niet tot theoretische studies. Toen bleek dat hij niet over lenzen van voldoende kwaliteit kon beschikken, ging hij zijn eigen lenzen slijpen, daarbij geholpen door zijn broer Constantijn. De broers werden bekwame lenzenslijpers, en hun lenzen waren van een voor die tijd ongekende kwaliteit. Een andere verbetering bestond uit een door Christiaan ontworpen oculair, dat was opgebouwd uit twee lenzen. Dit oculair, dat bekend staat als het ‘Huygens-oculair’, wordt ook tegenwoordig nog veel gebruikt. Het werk had belangrijke gevolgen. Met een eigengemaakte telescoop ontdekte Huygens in 1655 een satelliet van Saturnus, die later de naam Titan zou krijgen. Enige tijd daarna volgde de bevestiging van zijn hypothese dat de raadselachtige ‘armen’ van Saturnus in werkelijkheid een ring waren. In die tijd was het niet ongebruikelijk om belangrijke ontdekkingen in de vorm van een anagram te publiceren, om op deze wijze de prioriteit te verzekeren, zonder op de inhoud van de ontdekking te hoeven ingaan. Van deze mogelijkheid maakte Huygens ook gebruik. Hij legde zijn ontdekkingen aan Saturnus vast in twee anagrammen, die hij vervolgens openbaar maakte. In het geval van de satelliet in een brief aan de Engelse geleerde Wallis^8., in het geval van de ring aan het eind van het pamflet De Saturni Luna Observatio Nova (1656), waarin hij melding maakte van zijn ontdekking van Titan. Een uitgebreide publikatie over de resultaten van de waarnemingen aan Saturnus verscheen in 1659: Systema Saturnium.

Inmiddels had Huygens zijn eerste reis naar Parijs gemaakt. Hij bracht de zomer van 1655 in deze stad door, en hij voelde zich er zeer op zijn gemak. Tijdens bijeenkomsten ten huize van Habert de Montmor, een welgesteld begunstiger der wetenschappen, leerde hij veel belangrijke mensen kennen, zoals de filosoof Gassendi en de wiskundige Roberval. Hij nam deel aan de discussies over de laatste ontwikkelingen in de wiskunde en de natuurwetenschappen, en maakte kennis met voor hem nieuwe problemen. Naar aanleiding van deze bijeenkomsten raakte Huygens geïnteresseerd in de kansrekening. Eigen onderzoek op dit gebied leidde tot het zeer originele Tractaet handelende van Reeckening in Speelen van Geluck, dat in 1657 in Latijnse vertaling werd uitgegeven, en later, in 1660, in het oorspronkelijke Nederlands. In dit werk worden de grondslagen gelegd voor de moderne waarschijnlijkheidsrekening. Niet zonder reden noemen Jan en Annie Romein Huygens ‘Ontdekker der waarschijnlijkheid’!

Na de met enige tegenzin in september 1955 ondernomen terugreis naar Nederland begon voor Huygens een periode van hard werken. Behalve met zijn studie op het gebied van de kansrekening hield hij zich bezig met een ogenschijnlijk zeer praktisch probleem: het ontwerpen van een nauwkeurig lopende klok. Vooral voor de

8. Oeuvres, deel I, p. 331.

[p. 285]

zeevaart was zo'n instrument van groot belang, omdat het kon dienen als hulpmiddel bij de lengtebepaling op zee, in die tijd één van de grootste problemen bij de navigatie. Er waren verscheidene prijzen uitgeloofd (onder andere door de koning van Spanje) voor een bruikbare oplossing van dit probleem. In 1657 werd naar Huygens' ontwerp een uurwerk geconstrueerd waarbij een slinger zorgde voor een regelmatige gang. Het idee om een slinger te gebruiken was niet nieuw - Galilei had al geprobeerd dit denkbeeld in praktijk te brengen - maar tegenwoordig is men het erover eens dat Huygens de eerste was die een bruikbaar slingeruurwerk ontwierp. In de zeventiende eeuw was men nog niet zo eensgezind. Huygens' prioriteit bleef lange tijd omstreden, voornamelijk ten gunste van Galilei's zoon Vincenzio. Het slingeruurwerk had veel succes. De Haagse klokkenmaker Coster construeerde een groot aantal van deze uurwerken, die ook als torenklok zeer goed bruikbaar bleken. Al in 1658 werden in Scheveningen en in de Domtoren te Utrecht slingeruurwerken geïnstalleerd. Alleen op zee voldeden ze niet, omdat de onregelmatige scheepsbewegingen de werking te veel beïnvloedden. Het probleem van de lengtebepaling op zee bleef Huygens de rest van zijn leven bezighouden. In 1665 verscheen Kort Onderwijs aengaende het gebruyck der Horologien tot het vinden der Lenghten van Oost en West, waarin het gebruik van klokken bij de lengtebepaling wordt uiteengezet. Zijn pogingen om het slingeruurwerk voor gebruik op zee geschikt te maken leidden in 1675 tot een uurwerk met een ‘onrust’ in plaats van een slinger, terwijl een spiraalveer de gewichten verving. Dit ontwerp, dat in alle mechanische horloges nog steeds wordt toegepast, zou uiteindelijk succes hebben, maar dat heeft Huygens niet meer meegemaakt.

Het belang van Huygens' uitvinding kan moeilijk worden overschat. Niet alleen in de zeevaart was er behoefte aan nauwkeurige tijdmeting, maar ook in de wetenschap - met name in de astronomie - en in het dagelijks leven. Dankzij Huygens hoefde men zich niet langer te behelpen met zeer onbetrouwbare klokken, maar kon men eindelijk het verloop van de tijd op nauwkeurige wijze meten. De mens had de tijd onder controle gekregen!

Vanzelfsprekend beperkte Huygens zich niet tot de louter technische kant van zijn uurwerk. Hij wilde de werking van het apparaat ook theoretisch goed funderen. Uit een grondige studie van de slingerbeweging kwamen een aantal belangrijke resultaten voort, zowel op het gebied van de mechanica als op dat van de zuivere wiskunde. Op grond van deze resultaten kon de klok nog verder verbeterd worden. Een gedeelte van dit werk werd in 1658 gepubliceerd onder de titel Horologium.

Parijs liet Huygens niet los. In oktober 1660 vertrok hij voor de tweede maal naar deze stad. Hij was inmiddels zo beroemd geworden dat koning Louis XIV hem in audiëntie ontving. Ook ditmaal nam hij weer met veel enthousiasme deel aan de bijeenkomsten bij De Montmor. Via Londen, waar hij kennis maakte met Boyle (naar wie de aan elke middelbare scholier bekende Wet van Boyle is genoemd) keerde hij in het voorjaar van 1661 naar huis terug. Niet voor lang. Al in april 1663 reisde hij weer naar Parijs, deze keer als begeleider van zijn vader, die een diplomatieke missie moest vervullen. Vanuit Parijs bezocht hij in de zomer van 1663 Londen, waar hij werd opgenomen in de pas opgerichte Royal Society, een onder bescherming van de Engelse koning staand gezelschap van geleerden.

In Parijs was intussen een gunstig klimaat ontstaan voor wetenschapsmensen zoals Huygens. De nieuwe eerste minister van de Zonnekoning, Colbert, wilde Frankrijk tot een middelpunt op cultureel en wetenschappelijk gebied maken. Op zijn instigatie besloot de koning stipendia toe te kennen aan een aantal belangrijke kunstenaars en geleerden, waaronder Huygens. Nog voor zijn terugkeer naar Nederland in mei 1664 ontving hij de voor die tijd aanzienlijke som van 1200 livres. Naar het voorbeeld van de Royal

[p. 286]

Society wilde Colbert verder een Académie des Sciences oprichten, die, tot meerdere glorie van de koning, de taak van het organiseren van wetenschappelijke bijeenkomsten moest overnemen van particulieren zoals De Montmor. Het was Colberts bedoeling dat Huygens in deze Académie een vooraanstaande positie zou innemen. Het oprichten van de Académie nam nog vrij veel tijd in beslag. Het duurde tot 1666 voordat het zover was dat Huygens naar Parijs kon verhuizen om met zijn werk te beginnen. Hij ontving een jaargeld van de koning ter grootte van 6000 livres, meer dan enig ander Académielid kreeg. Bovendien woonde hij in een apartement in de Bibliothéque Royale, die gevestigd was in het gebouw waar ook de zittingen van de Académie plaatsvonden. Maar Huygens was dan ook vanaf de oprichting de onbetwiste leider van de Académie.

Twee maal per week kwam de Académie bijeen, op woensdag en op zaterdag. Op woensdag wijdde men zich aan de wiskunde, met inbegrip van mechanica en astronomie, op zaterdag aan de ‘natuurkunde’, waaronder ook de gehele biologie viel. Huygens stelde zelf een aantal wetenschappelijke programma's op^9., waarin de voornaamste taken van de Académie werden vastgelegd. Sommige van deze taken waren zeer praktisch van aard, zoals het op schepen meezenden van slingeruurwerken om hun bruikbaarheid te testen, het bepalen van de lichtsnelheid en het meten van de omtrek der aarde. In deze programma's kwam ook de astronomie uitgebreid aan de orde en de Académie zou zich dan ook intensief met astronomische waarnemingen bezighouden, daarbij geholpen doordat men kon beschikken over uitstekende, door Huygens ontworpen, telescopen, en nauwkeurige, eveneens door Huygens ontworpen, slingeruurwerken. Dat de astronomie zo'n belangrijke plaats innam is niet zo verwonderlijk als men bedenkt dat het deze wetenschap was die de in de zeventiende eeuw plaatsvindende vernieuwing - Dijksterhuis gebruikt terecht het woord ‘mechanisering’ - van het wereldbeeld op gang had gebracht.

Bij al deze concrete bezigheden stond Huygens een zeer algemeen doel voor ogen. In een stuk dat hij tussen 1666 en 1668 opstelde^10., schreef hij, nadat hij eerst was ingegaan op het belang van het verzamelen van zoveel mogelijk kennis over de natuur:

‘L'autre qu'on s'y doit proposer est la connoissance des causes qui consiste en une parfaite intelligence de la conformation de tous les corps physiques et des causes des effects qu'on en observe. dont l'utilitè seroit infinie quand quelque jour on en sera venu au bout. donnant moyen aux hommes d'emploier utilement les choses creees, avec certitude des effects qu'elles produiront.’

In het tweede deel van dit citaat komt de instelling tot uiting die men toen in het algemeen had tegenover wetenschappelijk onderzoek: men wilde het nut ervan vooral niet uit het oog verliezen. Dat gold ook voor Huygens, die, zoals we zagen, al vroeg geen bevrediging meer vond in puur wiskundige problemen.

Met zijn benoeming in de Académie begon voor Huygens een verblijf in Parijs dat, met twee onderbrekingen, tot 1681 zou duren. Van 1670 tot 1671 en van 1676 tot 1678 was hij in Nederland, in beide gevallen om te herstellen van een ernstige ziekte. Het is misschien overdreven te zeggen dat zijn Parijse periode de meest belangrijke in Huygens' leven was. Ook vóór 1666 had hij immers al zeer grote prestaties geleverd. Maar het is zeker dat hij in Parijs in een omgeving verkeerde waarin hij enorm werd gestimuleerd in zijn wetenschappelijk werk. Hij genoot er groot aanzien en had het zeer naar zijn zin. In Parijs ontstonden twee belangrijke werken: Horologium Oscillatorium (1673) en Traité de la Lumière, dat pas in 1690 werd gepubliceerd.

Het Horologium Oscillatorium, dat in het algemeen als Huygens' hoofdwerk wordt beschouwd, bevat de resultaten van zijn onderzoekingen naar aanleiding van het slingeruurwerk. Sommige gedeelten zijn technisch van aard, andere puur wiskundig. In het technische ge-

9. Oeuvres, deel VI, p. 95; deel XIX, pp. 254-271.

10. Oeuvres, deel XIX, p. 269.

[p. 287]

deelte wordt uiteengezet hoe een slingeruurwerk is opgebouwd. Het hier beschreven ontwerp is zo goed doordacht, dat het sindsdien slechts op enkele ondergeschikte punten kon worden verbeterd. Dit succes berust voor een belangrijk gedeelte op Huygens' inzicht dat het belangrijkste onderdeel van een klok wordt gevormd door het regulerende element, in dit geval de slinger. Het wiskundige gedeelte is dan ook gewijd aan een grondige studie van de slingerbeweging. Huygens besteedde veel aandacht aan het verschijnsel dat de slingertijd van een slinger toeneemt naarmate zijn maximale uitslag groter wordt, en hij slaagde erin de slinger zodanig op te hangen dat deze tekortkoming werd opgeheven.

Strikt genomen was de bestaande slingertheorie alleen van toepassing op slingers die bestonden uit een puntvormig gewicht, opgehangen aan een gewichtloze draad (‘ideale slingers’). Het lukte Huygens nu om ook het geval te behandelen waarbij rekening gehouden wordt met het gewicht van de afzonderlijke onderdelen van de slinger (de ‘fysische slinger’). Ten slotte geeft Huygens in een van de rest van het Horologium Oscillatorium losstaand gedeelte de wetten die de middelpuntvliedende kracht beschrijven. Deze wetten had hij al veel eerder afgeleid. Ze komen voor in een uit 1659 daterend manuscript, dat onder de titel De Vi Centrifuga in de Opuscula Posthuma verscheen.

In het Traité de la Lumière wordt een geheel nieuwe theorie voor het licht uiteengezet, en met succes gebruikt om een verklaring te geven voor een al lang bekend raadselachtig verschijnsel: de dubbele breking van licht in kalkspaat. Met dubbele breking wordt bedoeld dat een lichtstraal, die op een kristal kalkspaat valt, zich in het kristal als twee stralen voortzet. Dit verschijnsel kon door Huygens op fraaie wijze worden verklaard. Overigens vonden ook minder spectaculaire eigenschappen van het licht, zoals terugkaatsing en (gewone) breking, in de theorie een eenvoudige verklaring.

Huygens' lichttheorie wordt vaak een golftheorie genoemd, maar de naam ‘stoottheorie’ is juister. Men moet zich daarbij de volgende voorstelling maken. Op een biljart ligt een rijtje biljartballen. De ballen liggen langs een rechte lijn tegen elkaar. Een andere bal ligt apart, in het verlengde van het rijtje. Stoot men nu deze bal zó naar het rijtje, dat hij de bal aan het uiteinde precies in het midden raakt, dan zal hij na de botsing tot stilstand komen. Vrijwel tegelijkertijd zal de bal aan het andere uiteinde wegrollen, en wel met een snelheid die even groot is als die van de gestoten bal vóór de botsing. (Voor het gemak hebben we de wrijving met het laken verwaarloosd.) Het belangrijke punt is nu dat de ballen in het rijtje, op de wegrollende na, tijdens de botsing niet hebben bewogen, maar wel de ‘stoot’ hebben doorgegeven. Er is hier dus sprake van het doorgeven van snelheid (beter is: van impuls, dat is massa maal snelheid) door stilliggende deeltjes. In het geval waarbij elke bal geheel door andere ballen wordt omringd, zal de impuls niet in één richting worden doorgegeven, maar in alle richtingen. Elke bal fungeert dan op zijn beurt als ‘doorgeefcentrum’. Huygens gebruikte dit mechanisme om de voortplanting van het licht te verklaren. Hij postuleerde het bestaan van een overal aanwezige tussenstof, de ‘ether’, die hij zich opgebouwd dacht uit zeer kleine, zeer dicht opeengepakte harde deeltjes. Licht was nu volgens Huygens niets anders dan een onregelmatige opeenvolging van stoten, die zich vanuit elk punt van een lichtbron op de zojuist beschreven manier door de ether voortplanten. Door uit te gaan van het feit dat elk etherdeeltje als doorgeefcentrum optreedt, kon hij aantonen dat de stoten zich bolvormig door de ruimte uitbreiden. In Figuur 2 zijn de bollen getekend die horen bij de punten A, B en C in de kaarsvlam.

Een van Huygens' uitgangspunten bij het opstellen van zijn lichttheorie was het recente empirische resultaat dat de voortplantingssnelheid van het licht een eindige grootte heeft. Men had lange tijd gedacht dat licht een instantaan verschijnsel is (dat wil zeggen: zich met oneindige snelheid voortplant), maar in 1676 was de Deense astronoom Rømer op grond van waarnemingen

[p. 288]

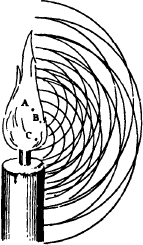Figuur 2: de bolvormige voortplanting van het licht. (Uit: Traité de la Lumière.)

aan de manen van Jupiter tot de conclusie gekomen dat de lichtsnelheid eindig is. Huygens was overtuigd van de juistheid van deze conclusie. Uit Rømers waarnemingen schatte hij de lichtsnelheid op ruim 200 000 km/s. (De juiste waarde is bijna 300 000 km/s.)

Tussen Huygens' stoottheorie en een echte golftheorie is eigenlijk maar weinig verschil. Zodra de stoten de lichtbron met regelmatige tussenpozen verlaten, ontstaat een echte golfbeweging of trilling, waarbij de trillingsrichting dezelfde is als de voortplantingsrichting (een ‘longitudinale’ trilling). Huygens heeft het zelf ook vaak over ‘golven’ in plaats van ‘stoten’, hoewel dat strikt genomen dus niet juist is. Ook in een golftheorie plant het licht zich bolvormig in de ruimte voort. De bolvormige begrenzingen heten nu ‘golffronten’. In zo'n theorie wordt het principe dat elk etherdeeltje als doorgeefcentrum fungeert meestal uitgedrukt doordat men zegt dat elk punt van een golffront zelf bron is van nieuwe, secundaire golffronten. Dit principe, dat van toepassing is op alle golfverschijnselen in een materieel medium, staat bekend als het ‘Principe van Huygens’.

In het Rampjaar 1672 ontstond voor Huygens een moeilijke situatie. Zijn besluit in Parijs te blijven vond in Nederland weinig begrip en er werd hem gebrek aan vaderlandslievendheid verweten. Ten onrechte. Huygens volgde de oorlogsontwikkelingen met aandacht en hij voelde zich bij de Nederlandse zaak betrokken. Maar het wetenschappelijk werk ging voor. Het onbegrip in Nederland werd nog groter toen hij het volgende jaar het Horologium Oscillatorium bij het verschijnen aan de Franse koning opdroeg. Voor Huygens stond die opdracht los van gevoelens van loyaliteit tegenover welk land dan ook. Het was meer een kwestie van beleefdheid tegenover zijn beschermheer, van wie hij bovendien nog financieel afhankelijk was. Ook was hij zich ervan bewust dat hij als Nederlander in Parijs een enigszins delicate positie innam, en dat het ontbreken van de opdracht zijn positie zou kunnen verzwakken.

In 1681 werd Huygens voor de derde maal zo ernstig ziek dat hij naar Nederland moest terugkeren om daar in alle rust te herstellen. Hij zou Parijs niet terugzien. Toen hij twee jaar later weer beter was, en plannen begon te maken voor zijn terugkomst, bleek dat men in Parijs op zijn aanwezigheid geen prijs meer stelde. Na de dood van Colbert in 1683 was in Frankrijk een atmosfeer van onverdraagzaamheid ontstaan die vooral tegen protestanten gericht was, en die in 1685 zeer duidelijk tot uiting kwam in de herroeping van het Edict van Nantes. Huygens was het slachtoffer geworden van dit anti-protestantisme, dat nog versterkt werd door gevoelens van rivaliteit binnen de Académie. Hij bleef dus in Nederland. Samen met zijn vader bracht hij de zomers door in diens buitenverblijf Hofwijck te Voorburg, en de winters in Den Haag. Nadat zijn vader in 1687 op negentigjarige leeftijd was overleden, woonde hij alleen.

Nog éénmaal ondernam Huygens een grote reis. Een gedeelte van de zomer van 1689 bracht

[p. 289]

hij in Engeland door, waar hij verscheidene ontmoetingen had met de man die langzaam bezig was hem te overvleugelen: Isaac Newton. Het is jammer dat we vrijwel niets weten over het verloop van deze ontmoetingen. Een reis samen met Newton per postkoets van Cambridge naar Londen wordt in het dagboek, dat Huygens van zijn verblijf bijhield, zelfs met geen woord vermeld. Het is vooral daarom zo jammer, omdat Newton en Huygens op een aantal punten fundamenteel van mening verschilden.

In Newtons hoofdwerk Philosophiae Naturalis Principia Mathematica (1687) speelt het begrip ‘kracht’ een geheel andere rol dan in de mechanica van Huygens. Bij Newton is het voldoende als men weet wat de werking van een kracht is; naar de oorzaak van de kracht wordt niet gevraagd. Kracht is een basisbegrip. Dit uitgangspunt was volstrekt in strijd met Huygens' mechanicisme, dat eiste dat voor elke kracht een oorzaak moest worden gevonden in de vorm van direct contact tussen stoffelijke lichamen. Ook het begrip ‘werking op afstand’ was voor Huygens onaanvaardbaar. Dit begrip treedt bij Newton op in verband met de zwaartekracht, en houdt in dat deze kracht zich niet in een tussenstof voortplant, maar instantaan over elke afstand werkzaam is. Huygens' theorie voor de zwaartekracht was strikt mechanistisch van aard. In het Discours de la Cause de la Pesanteur, dat in 1690 in één band met het Traité de la Lumière verscheen, ging hij uit van het bestaan van een ‘subtiele materie’, samengesteld uit zeer kleine deeltjes (nog kleiner dan de etherdeeltjes) die de aarde met zeer grote snelheid in alle richtingen omcirkelen. Volgens Huygens werd de zwaartekracht veroorzaakt doordat stoffelijke lichamen door botsingen met de rondwervelende deeltjes naar de aarde werden gedreven. In deze theorie, die voortbouwt op denkbeelden van Descartes, konden een aantal belangrijke verschijnselen, zoals het feit dat de versnelling van de zwaartekracht voor alle lichamen gelijk is, niet bevredigend worden verklaard. Het is daarom niet verwonderlijk dat Newtons theorie, die veel minder gekunsteld was, en ook experimenteel uitstekend voldeed, al spoedig algemeen aanvaard werd. Het is interessant erop te wijzen dat in onze tijd de opvattingen over de aard van krachten - of wisselwerkingen, zoals men liever zegt - in zekere zin weer meer mechanistisch zijn geworden. In de nieuwste quantummechanische theorieën worden wisselwerkingen tussen deeltjes altijd beschreven met behulp van andere deeltjes die de wisselwerking ‘dragen’, dat wil zeggen van het ene deeltje op het andere overbrengen. Het begrip ‘werking op afstand’ komt in deze theorieën volstrekt niet meer voor. Men moet zich overigens hoeden voor al te aanschouwelijke voorstellingen bij deze theorieën. In de meeste gevallen hebben de uitgewisselde deeltjes zo'n korte levensduur dat we nauwelijks nog van deeltjes kunnen spreken.

Ook over de aard van het licht hadden Newton en Huygens verschillende opvattingen. Huygens' theorie hebben we al uiteengezet. Volgens Newton bestond het licht uit een stroom deeltjes. Net als bij de zwaartekracht werd de theorie van Huygens al spoedig verworpen ten gunste van die van Newton. Maar in de negentiende eeuw kwam men op grond van experimenten tot de conclusie dat Newtons theorie niet juist was, en moest worden vervangen door een golftheorie. Tegenwoordig kent men aan het licht zowel deeltjes- als golfeigenschappen toe.

Een derde punt van meningsverschil tussen Huygens en Newton betrof de relativiteit van beweging. We zagen al hoe Huygens het relativiteitsprincipe voor eenparig rechtlijnige bewegingen formuleerde, en op botsingsverschijnselen toepaste. Maar hij ging verder. Hij poneerde dat aan alle bewegingen, dus ook aan rotaties, een relatief karakter moest worden toegekend, dat absolute beweging niet bestaat. Dit was in strijd met Newtons denkbeelden. Newton beweerde dat rotaties absoluut waren, en lichtte dit toe door erop te wijzen dat bij rotaties altijd middelpuntvliedende krachten optreden. Zet men een met water gevulde emmer op een ronddraaiend platform, dan zal het water tegen de binnenwand

[p. 290]

van de emmer omhoogkruipen. Ook een waarnemer op het platform, voor wie de emmer dus in rust is, zal dit dynamische effect waarnemen. Daarmee is, volgens Newton, het absolute karakter van rotaties aangetoond. Volgens hem vinden rotaties plaats ten opzichte van de ‘absolute ruimte’, die absoluut in rust is. Hoewel Huygens deze conclusie niet accepteerde, heeft hij nooit een overtuigende alternatieve verklaring kunnen geven voor het dynamische effect dat bij rotaties optreedt. De negentiende-eeuwse fysicus en filosoof Ernst Mach kon dat wel. Hij stelde^11. dat de dynamische effecten het gevolg zijn van wisselwerkingen tussen ten opzichte van elkaar bewegende massa's. Bij de bovenbeschreven proef met de emmer is de rotatie relatief ten opzichte van de ‘vaste sterren’. De zwaartekrachtswerking van deze sterren zorgt voor het dynamische effect. Als men in staat zou zijn de sterrenhemel rond te laten draaien, dan zou in een stilstaande emmer het wateroppervlak hol worden. Hiermee hebben rotaties hun absolute karakter verloren. Dit ‘Principe van Mach’ heeft Einstein later geinspireerd bij het opstellen van zijn Algemene Relativiteitstheorie. In de moderne natuurkunde komen de begrippen ‘absolute ruimte’ en ‘absolute beweging’ niet meer voor.

Ook in de jaren na 1683 bleef Huygens op allerlei gebieden actief. Hij hield zich bij voorbeeld bezig met het ontwerpen van een planetarium, dat werd aangedreven door een volgens zijn instructies vervaardigd uurwerk met onrust en spiraalveer. Bij de berekeningen voor dit ontwerp gebruikte hij de nieuwe wiskundige techniek der kettingbreuken. Verder besteedde hij veel aandacht aan de optica. Hij schreef een verhandeling over het slijpen van lenzen getiteld Memorien aengaende het slijpen van glasen tot verrekijckers, die in Latijnse vertaling in de Opuscula Posthuma verscheen, en deed uitvoerige waarnemingen, zowel met telescopen als met microscopen. In Astroscopia Compendiaria (1684) beschreef hij de door hem ontworpen buisloze telescoop. Ook de wiskunde behield zijn belangstelling. Hij bestudeerde de differentiaalen integraalrekening en correspondeerde met Leibniz over deze nieuwe methoden. Tot eigen toepassingen kwam het echter niet. Op het gebied van de muziektheorie kwam Huygens in 1691 met het originele voorstel om het octaaf in 31 gelijke delen te verdelen, in plaats van de gebruikelijke 12. Ten slotte vermelden we Huygens' speculaties over de mogelijkheid van het bestaan van leven op andere planeten, die hij in de laatste jaren van zijn leven tot een boek verwerkte. Onder de titel Cosmotheoros (letterlijk: beschouwer van het heelal) verscheen het na zijn dood, in 1698. In dit boek verdedigt hij de stelling dat het onwaarschijnlijk is dat de aarde de enige planeet is waarop levende wezens voorkomen, en hij komt tot de conclusie dat leven op andere planeten in zijn verschijningsvorm niet veel zal verschillen van dat op aarde. Cosmotheoros bevat ook gedeelten die puur astronomisch van aard zijn, zoals het deel waarin Huygens berekent hoe de bewegingen van de hemellichamen er vanaf andere planeten zullen uitzien.

In het voorjaar van 1695 werd Huygens ziek. Het was dezelfde kwaal die hem al eerder had getroffen. Over de aard van deze ziekte weten we weinig. Een van de symptomen was een diepe neerslachtigheid, maar hij had ook periodes waarin hij^12. ‘soo aengingh ende sulcke desperate dingen sprack, dat men daer vervaert af wierd’. Verder sloeg hij soms godslasterlijke taal uit, en maakte hij toespelingen op zijn onorthodoxe opvattingen over het geloof. Zijn rationalisme maakte het hem zeer moeilijk, zo niet onmogelijk, in het bestaan van een alles bestierend opperwezen te geloven, hoe zwaar hem dat wellicht ook viel. Een dominee die hem op zijn ziekbed bezocht kon daarin geen enkele verandering brengen. Die dominee was hem, ongevraagd, door zijn familie gezonden, nadat een eerdere poging om zijn toestemming voor zo'n bezoek te krijgen was mislukt, omdat^13. ‘hij begon te vloecken en te raesen’. Eind juni ging Huygens' toestand snel achteruit. Hij overleed

11. Ernst Mach, Die Mechanik, Leipzig, 1883.

12. Oeuvres, deel XXII, p. 766.

13. Oeuvres, deel XXII, p. 767.

[p. 291]

op 8 juli 1695, waarschijnlijk in zijn woning aan het Haagse Noordeinde. Op 17 juli werd Christiaan Huygens begraven in het familiegraf in de St. Jacobskerk in Den Haag.

Tot slot nog enkele opmerkingen over de persoonlijkheid van Huygens. Men zou de indruk kunnen krijgen dat Huygens maar voor één ding belangstelling had in het leven: de wetenschap. Dat is niet juist. Hoewel de wetenschap voor hem op de eerste plaats kwam, en hij teruggetrokken van aard was, leidde hij niet het leven van een kluizenaar. In Parijs en Den Haag nam hij deel aan het culturele leven, bij voorbeeld door het bezoeken van concerten en toneelvoorstellingen. Uit het feit dat Huygens zijn gehele leven vrijgezel is gebleven, mag men niet afleiden dat hij een afkeer had van vrouwelijk gezelschap. In zijn laatste jaren had hij dikwijls gezelschap van een zekere Madame la Ferté, over wie de vrouw van Constantijn junior schreef^14. dat Christiaan ‘sijn hart met haer wel soude konnen ophaelen, want dat men seyde dat sij niet seer cruelle en was’.

We hopen dat uit dit artikel enigszins is gebleken hoe jammer het is dat Huygens in onze tijd zo weinig bekend is. Ook een hedendaags lezer kan nog worden geboeid en geïnspireerd door de veelzijdigheid en de kwaliteit van zijn werk.

14. Oeuvres, deel XXII, p. 387.

Literatuur

Het verzameld werk van Christiaan Huygens is op voorbeeldige wijze uitgegeven in de 22 delen tellende Oeuvres complètes de Christiaan Huygens, publiées par la Societé Hollandaise des Sciences, Den Haag 1888-1950. (Hierna afgekort als: Oeuvres). Deze uitgave omvat ook Huygens' correspondentie. Deel XXII bevat een biografie door J.A. Vollgraff.

Literatuur over Huygens:

A.E. Bell, Christian Huygens and the Development of Science in the Seventeenth Century, Londen, 1947.

H.J.M. Bos, Christiaan Huygens, in: C.C. Gillispie (Ed.), Dictionary of Scientific Biography, Vol. VI, p. 597, New York, 1972.

H.L. Brugmans, Le séjour de Christiaan Huygens à Paris et ses relations avec les milieux scientifiques français, suivi de son journal de voyage à Paris et à Londres, Parijs, 1935.

E.J. Dijksterhuis, De mechanisering van het wereldbeeld, pp. 405, 504, Amsterdam, 1975 (2e druk).

Jan en Annie Romein, Christiaen Huygens, Ontdekker der waarschijnlijkheid, in: Erflaters van onze beschaving, Amsterdam, 1977 (12e druk).

Noten

Een eerdere versie van dit artikel verscheen in Intermediair (15e jaargang, no. 8, 23 februari 1979).