Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 542]
| |
IV Methodus LeibnitijGa naar voetnoot1).
| |
[pagina 543]
| |
CO applicata ejus, AO abscissa. CT tangens in C. AO ∞ x. OC ∞ y. a linea data. OT ∞ t subtangens, semper est aa/x. Quaeritur natura ac constructio curvae MC.  DF est hyperbola ad asymptotos AM, AE, cujus quadratum AMDE. MG facit angulum GMH dimidium recti. Jam ducta GHC parallela MA, oportet in ea punctum curvae C ita situm esse ut ducta CBF parallela AO, fiat spatium hyperbolicum BFDM aequale spatio seu triangulo GHM. Si ergo possim triangulo GHM abscindere aequale spatium hyperbolicum BFDM, hoc est si detur quadratura hyperbolae, potero construere curvam MC. Poterat et FBC prima duci, in qua punctum C ita accipiendum ut ducta CG fiat triangulum GMH aequale spatio BFDM. Si subtangens  hoc est si hoc est si  [Fig 126] [Fig 126]
 [Fig. 126]
| |
[pagina 544]
| |
 Haec curva MC construi poterit datis quadraturis Hyperbolae et Circuli. Oportet enim punctum ejus quodlibet C ita esse positum ut ductis CF, CG, spatium hyperbolicum MDFB fiat aequale spatio circulari MLGH. Et semper adeo spatiolum BR aequale spatiolo HS; hoc est  . Jam erit subtangens OT sive . Jam erit subtangens OT sive  . Patet aad . Patet aad , ut in superiori exemplo, esse spatiolum BR hyperbolicum; et , ut in superiori exemplo, esse spatiolum BR hyperbolicum; et  esse spatiolum circulare HS. esse spatiolum circulare HS.
Locus est methodo huic ut ait Leibnitius, quandocunque quantitas subtangentem datam constituens oritur ex ductu vel divisione quantitatum quae praeter datas quantitates tantum x vel y habent, non utrumque simul. Sic subtangens  non admittitur. nec non admittitur. nec  ; nec ; nec  . quae postrema Fatij methodum admittit. estque subtangens parabolae. . quae postrema Fatij methodum admittit. estque subtangens parabolae.
Methodus haec in eo posita est, ut ad aequationem perveniatur in qua ex una parte non habeatur nisi x et dx; ex altera non nisi y et dy, praeter quantitates cognitas, nec succedit nisi cum hoc fieri potest; cum vero potest, deducitur problema ad quadraturas. Il est vrai que Leibnitz n'avait pas fait connaître sa méthode en entier; voyez les p. 224 et 227 du T. X. Nous empruntons encore à la p. 9 du Manuscrit H ce qui se rapporte à la logarithmique.  formula generalis. Ergo formula generalis. Ergo  formula cum t datur per y, vel cum t ∞ a. Sit t ∞ a, semper subtangens data [comparez le § 18 qui précède]. formula cum t datur per y, vel cum t ∞ a. Sit t ∞ a, semper subtangens data [comparez le § 18 qui précède].
 sive sive  . Hic altero a multiplicavi ut fieret . Hic altero a multiplicavi ut fieret  spatium hyperbolicum. Poterat et per b pro a. spatium hyperbolicum. Poterat et per b pro a.
 Ad aequationem x ∞  producit Leibnitius. ex qua obscura adhuc manet curvae constructio. Imo ne a quidem adsumit, sed ponit t ∞ 1, unde ipsi aequalis producit Leibnitius. ex qua obscura adhuc manet curvae constructio. Imo ne a quidem adsumit, sed ponit t ∞ 1, unde ipsi aequalis  . Unde concludit curvam quaesitam pendere à quadratura hyperbolae quod plane obscurum est unde constet. . Unde concludit curvam quaesitam pendere à quadratura hyperbolae quod plane obscurum est unde constet.
| |
[pagina 545]
| |
Haec curva MC [Fig. 127], quae est Logarithmica, construi poterit data quadratura hyperbolae. Oportet enim ejus punctum quodlibet C ita esse positum ut ductis
 [Fig. 127]
CF, CG, spatium hyperbolicum MDFB, aequetur rectangulo HL, adeoque semper spatiolum BR rectangulo minimo HS. Hoc est semper  . Unde patet si aequalia sint spatiola BR, ZF, etiam aequalia debere esse spatiola KG, GY, ideoque et lineolas IO, Oλ. Spatiola autem BR, ZF sunt aequalia quando proportionales sunt . Unde patet si aequalia sint spatiola BR, ZF, etiam aequalia debere esse spatiola KG, GY, ideoque et lineolas IO, Oλ. Spatiola autem BR, ZF sunt aequalia quando proportionales sunt
 [Fig. 128]
RQ, FB, VZ; tumque etiam proportionales fiunt Rδ, Fγ, Vβ, hoc est NI, CO, θλ. Ergo ea est natura curvae MCθ, ut si NI, CO, θλ proportionales sint, simul rectae IO, Oλ sint aequales. quam scimus esse proprietatem Logarithmicae, cujus asymptotos AT. | |
[pagina 546]
| |
Et hujus quidem subtangens, ut OT, semper fiet aequalis a. Angulus quem curva facit ad MA est semirectus. Quod aliter fuisset [Fig. 128] si multiplicassem utrimque per b. unde  . Tunc enim rectangulum hyperbolae fuisset ab et curva MC exijsset à termino rectae b, si haec in asymptoto AL accepta fuisset, ut in hac figura. . Tunc enim rectangulum hyperbolae fuisset ab et curva MC exijsset à termino rectae b, si haec in asymptoto AL accepta fuisset, ut in hac figura.
NB. Potest quidem haec Curva Logarithmica per puncta quotlibet construi absque quadratura Hyperbolae, sed non ita ut subtangentem habeat datae huic aequalem, quod hic fecimus. |
|



 [Fig 124]. subtangens
[Fig 124]. subtangens 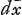 vel dx significat Leibnitio incrementum lineae x sive differentiolam duarum inaequalium proximarum x.
vel dx significat Leibnitio incrementum lineae x sive differentiolam duarum inaequalium proximarum x. 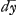 vel dy similiter incrementum lineae y . aa:y significat aa/y.
vel dy similiter incrementum lineae y . aa:y significat aa/y.
