Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 144]

N^o 94.
Fr. van Schooten à Christiaan Huygens.
30 juin 1651.

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 93.

Fr. à Schooten, Nobili ac rarae eruditionis Juveni-Viro, D. Christiano Hugenio S.P.D.

Negligentiae me forte accusabis Praestantissime Domine, Juvenum Ornatissime, utpote qui tuis, 13 May ad me missis, longo hoc intermisso tempore, nihil adhuc responsi dederim. Sed excusabis spero, cum intelliges me meorum transmigratione plura seponere debuisse, quae velut deperdita penes me tamdiu latuêre, donec mihi animus curis omnibus ac negotijs esset solutus. Quapropter postquam me studijs rursus accinxi, statim mihi in mentem venit, ut, quae de hoc loco, quem plane solidum ante credideram (quippe calculo deceptus) non satis distincte conceperam, ea accuratius examinare ac cum tuis conferre susciperem. Planum igitur illum esse vel nemini dubium videri poterit, qui tum Analysin vestram, tum demonstrationem hanc



meam planè est percepturus, quam itaque hìc subiungam.

Datis positione puncto A, et lineâ BD, in eaque puncto C; invenire E punctum, unde si ducatur EA ad datum punctum A, et ED ad datam positione lineam BD in angulo D, aequali dato AFB, sit rectangulum sub abscissâ DC et aliâ datâ AG aequale quadrato AE.

Constructio. Ductâ AG parallel â BD, agatur ex C ipsi AF parallela CI, donec secetur ab AG, productâ in I, et inveniatur inter IA, AG media proportionalis AL. Deinde, descripto super AG per 33.3¹⁾ circuli segmento AHG, quod capiat angulum AHG aequalem dato AFB, describatur ex ejus centro K circulus MELP, transiens per punctum L. Dico, si in ejus circumferentiâ utcunque sumatur punctum E,

1) Ces nombres désignent la proposition 33 du livre 3 des Eléments d'Euclide. Les citations suivantes ont une signification analogue.

[p. 145]

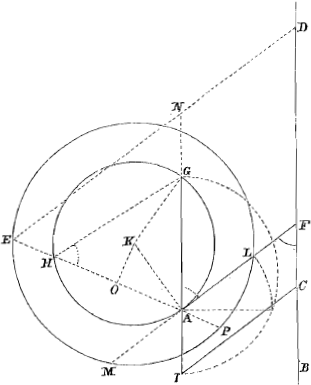
et ab ipso ad datum punctum A agatur EA, et ED ad positione datam DB in angulo dato D seu F, hoc est, ipsi AF parallela, rectangulum sub abscissâ CD et datâ AG aequari quadrato AE.

Demonstratio. Producantur enim FA, EA ad circumferentiam in M et P, et IG ad rectam ED in N, demissaque ex K in HA perpendiculari KO, jungatur HG. Quoniam igitur triangulorum AHG et ANE anguli ad H et N aequales sunt, et angulus ad A utrique communis: erit etiam tertius ad G tertio ad E aequalis, et triangulum AHG simile triangulo ANE. Quare erit per 4. 6 ut AH ad AG, ita NA ad AE, ac proinde per 16. 6 rectangulum EAH aequale rectangulo NAG. Deinde quoniam KO perpendicularis est ad HA, erit per 3. 3. HO aequalis OA, ut et EO aequalis OP. Quibus ab invicem subductis, relinquitur EH aequalis AP. Similiter cum KA per constructionem perpendicularis sit ad ML, erit et MA per 3. 3. aequalis AL. Hinc, cum per 35. 3 rectangulum EAP, hoc est, AEH aequale sit rectangulo MAL siue quadrato AL, et quadratum quidem AL per constructionem et 17. 6 aequale sit rectangulo IAG; erit quoque rectangulum AEH aequale rectangulo IAG. Aequalia igitur sunt bina rectangula EAH et AEH binis rectangulis NAG et IAG. Sunt autem bina rectangula EAH et AEH per 2. 2 simul aequalia quadrato totius AE. Bina vero rectangula NAG et IAG per 1. 2 simul aequalia rectangulo sub totâ IN, hoc est, abscissâ CD et datâ AG. Aequale ergo est rectangulum sub abscissâ CD et datâ AG quadrato ex AE. Quod erat faciendum.

Eâdem fermè ratione reliqui casus ad hujus imitationem construi ac demonstrari possunt, sed haec Tibi ostendisse sufficiant. Vale.

Tibi addictissimus

Fr. à Schooten.

Leydae Ultimo Junij 1651.

A Monsieur Monsieur, Christianus Huijgens, ten huijse van Mijn Heer van Zuijlechem, op t'plein

port

in

S'graven-hage.