Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 395]
| |
V. Progressio optima ad quadrandum circulum ac non tantum Leibnitiana multo citius appropinquans sed et Newtonianam post se relinquens simpliciorque ea ac commodior.
| |
[pagina 396]
| |
(Pièce III qui précède) peut être appelée le développement de l'arc tangente pour un arc de  ... pour t = 1Ga naar voetnoot2). ... pour t = 1Ga naar voetnoot2).
Le § 3 qui suit, lequel est antérieur en date au § 1, indique comment Huygens a obtenu sa formule: voyez les dernières lignes du § 3. Le § 4 amplifie cette explication. Le § 2, moins important, fait suite au § 1. | |
§ 2Ga naar voetnoot3). Potest quisque numerus seriei quadratricis inveniri ex promixe praecedenti, exigua multiplicatione et divisione unius vel duarum characterum, usque ad numerum decimum quintum. inde ad quinquagesimum multiplicatione per duos characteres et divisione per tres. quo compendio in suis progressionibus utebatur D. Fatius.
Fatio de Duillier, suisse, visita Huygens à la Haye en septembre 1686 (T. IX, p. 134) et de nouveau en février 1691 (T. X, p. 21; il resta à la Haye jusqu'en septembre, T. X, p. 440) après avoir séjourné en Angleterre et y avoir rencontré e.a. Newton. Voyez la note 1 de la p. 117 du T. IX et la suite du présent Tome. | |
[pagina 397]
| |
Nam si in serie 1/1.1 - 1/3.3 + 1/5.9 - 1/7.27 + 1/9.81 - 1/11.243 &c fractionum, quarum singulis denominatoribus dividi debet numerus 10000000000, ponamus m pro numero hoc; et m/d in p significet m divisum per denominatorem aliquem fractionum seriei ut d sit numerus progressionis 1, 3, 5, 7, &c. et p) potestas ternarij (unde fit numerus aliquis seriei quadratricis), erit numerus proximè sequens hujus seriei  . quem dico ex praecedenti illo m/d in p facile inveniri. Est enim m/d.p ad . quem dico ex praecedenti illo m/d in p facile inveniri. Est enim m/d.p ad  ut ut
 ad d.p, hoc est ut ad d.p, hoc est ut
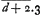 ad d. Est autem d + 2 numerus seriei 1, 3, 5, 7 in fractione proxime sequente. ad d. Est autem d + 2 numerus seriei 1, 3, 5, 7 in fractione proxime sequente.
Ergo posita serie 1, 3, 5, 7, 9, 11, 13 &c erit primus numerus seriei quadratricis nempe 10000000 &c ad secundum, ut triplum 3 ad 1, seu ut 9 ad 1. Secundus ad tertium ut triplum 7 ad 5, seu ut 21 ad 5 atque ita porro. Sed si in uno quopiam erratum fuerit, etiam in sequentibus omnibus errabitur. | |
§ 3Ga naar voetnoot4).BEπ [Fig. 59] cissoides. AD ad DC ut BD ad DE. Pour entendre le présent § on peut le comparer avec le § 1 bis de la p. 149 du T. XIX datant de 1674. La Fig. 79 ter de la p. 148 du T. XIX, laquelle appartient à ce § 1 bis, est analogue à la présente Fig. 59. Dans cette Fig. 79 ter BE est la cissoïde et BGFζ la courbe qui correspond à la courbe BFζ de la présente Fig. 59. Ostendimus olim spatium AEB aequari triplo segmento circuli CBS. Ergo et spatium [Fig. 59]
| |
[pagina 398]
| |
CEB aequabitur triplo segmento CBS, nam triangulum CDB ∞ ADE. Ergo spatium ECSB ∞ 4 segmentis CBS. Ergo et spat. DFB ∞ 4 segm. CBS. quia, ex constructione curvae BFζ - voyez son équation plus loin dans le présent §, et aussi dans la note 2 de la p. 149 du T. XIX -, spat. CSBF ∞ DEB. nam CF sumta est aequalis DE, et sic ubique. Ducatur AC et producta occurrat tangenti BG in L. Et sit QCG parallela AB. Quia ergo ut AD ad DC hoc est ut BD ad DE ita CG ad GL; erit GL ∞ DE seu CF. Unde juncta LF, parallela erit BA. Producatur LF ad M. Jam trianguli δCB duplum est triang. ACB. Ergo ▭ AG quadruplum trianguli δCB. Unde et ▭ DM quadruplum erit trianguli δCB. Sed spat. FBD erat quadruplum segmenti circuli CSB. Ergo totum spatium MFBA ∞ 4 sectores δCSB. Est autem 4 sector δCSB ∞ ▭ ab arcu CB et recta AB. Ergo spat. MFBA ∞ huic rectangulo. Ergo ▭ MB ad spat. MFBA ut LB ad arcum CB sive ad arcum OB, cujus ipsa LB tangens &c. Ex his sacile perspicitur spatium Aaζ B aequari circulo ACB, sive quadranti AaOBGa naar voetnoot5). Ceci correspond à la dernière ligne de la p. 149 du T. XIX. Quod si continuetur curva Bζ ut et asymptotos Aa, fiet spatium interjectum infinitum aequale quadruplo semicirculo ACB, hoc est duplo circulo ACπ. ut facile ex his colligiturGa naar voetnoot5). Sit AB ∞ a, AM ∞ x, MF ∞ y. Quia ergo AD. DC : BD. DE [c.à.d. AD : DC = BD : DE] erit et AD.DC : AB.CE vel DF. 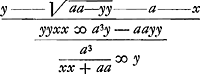 C'est l'équation, dont nous avons déjà parlé plus haut, de la courbe BFζ, connue plus tard sous le nom de versiera. Il n'est pas généralement connu que Huygens a considéré la versiera déjà en 1674. En margeGa naar voetnoot6): Ex hujus fractionis divisione numeris expressa oritur quadratura Leibnitsij. Ex qua circulus est ad quadratum circumscriptum ut 1 - ⅓ + ⅕ - 1/7 + 1/9 &c. ad 1. | |
[pagina 399]
| |
Voyez sur la ‘fractionis divisio’ et sur la sommation qui suit cette division, la note 57 de la p. 41 du T. X et la p. 147 du T. XIX. Consultez aussi la note 12 de cette dernière page. Et les p. 261-262 du présent Tome. Toujours en marge: Sed haec approximatio lente procedit. Multo citius appropinquabit si AM sive BL ponatur tangens parvi arcus certorum graduum. Sed tunc semper erit irrationalis. Vide pag. infra. Cette p. 63 du Manuscrit G - numération de Huygens - est la f. 82 v à laquelle nous avons emprunté le § 1 qui précède. | |
§ 4Ga naar voetnoot7).ABCD quadratum [Fig. 60]. BD quadrans circumferentiae, centro A, BN ∞ AB, CM ∞ CD. BM parabola cujus [Fig. 60.]
latus rectum BN. LQ parallela BA secans BC in K. LQ, KQ, PQ proportionales. BPpO per puncta P inventa est linea curva. En marge: Haec curva BPO est eadem quae folio praecedente [Fig. 59] BF ζ. AB ∞ a, AQ ∞ x, QP ∞ y,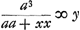 . .
Dico spatium BODA aequale esse quadranti ABDGa naar voetnoot8). Item ductâ utcumque AK quae secet arcum in G, et ex K deinde rectâ KQ quae secet curvam BPO in P. dico esse ½ arcum BD ad arcum BG sicut quadratum BD [lisez: quadrantem ABD] ad spatium BPQAGa naar voetnoot8). Applicetur ordinatim LR. Ductâ jam AH quae faciat minimum sectorem GAE et minimum simul triangulum KAH, erit hoc triangulum ad illum minimum sectorem ut qu. KA ad qu. AG, hoc est ut qu. AB + qu. BK ad qu. AB. hoc est ut qu. AB + ▭ ABR ad qu. AB. hoc est ut RA sive LQ ad KQ. Quod si igitur tota BC divisa intelligatur in particulas aequales ipsi KH, et a divisionum punctis ducantur rectae ad A, erit totum triangulum ABC divisum in totidem triangula aequalia. Et si ab ijsdem divisionum punctis ducantur parallelae ad BA, eae secabunt qu. BD in totidem rectangula aequalia. Et horum singula ad partes interceptas ejusdem latitudinis de spatio BODA, erunt ut rectae KQ ad PQ. hoc est ex constructione ut rectae LQ ad KQ, hoc est ut ∆la KAH ad sectores GAE. Sed et rectangula HQ et ∆la HAK sunt respective omnia inter se aequalia. Ergo ut omnia dicta ▭a ad omnia spatia PS, ita omnia ∆la KAH ad omnes sectores GAE. hoc est | |
[pagina 400]
| |
ut ▭ KA ad spat. BPQA ita ∆ KAB ad sectorem GAB, sive ita tangens KB ad arcum GB. &c.Ga naar voetnoot9). En marge: Hinc ergo etiam per continuam divisionem oritur Progressio Leibnitsij ad Circuli Quadraturam et ad sectores quosvis, quod ille nescio an animadverteritGa naar voetnoot10). |
|



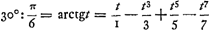 ..... pour t = 1/√ 3; tandis que celle de Leibniz
..... pour t = 1/√ 3; tandis que celle de Leibniz








