Logo DBNL
Bouwstoffen voor de geschiedenis der wis- en natuurkundige wetenschappen in de Nederlanden (1878)

Bouwstoffen voor de geschiedenis der wis- en natuurkundige wetenschappen in de Nederlanden

(1878)–David Bierens de Haan–rechtenstatus Auteursrechtvrij

Vorige Volgende

BOUWSTOFFEN VOOR DE GESCHIEDENIS der WIS- EN NATUURKUNDIGE WETENSCHAPPEN IN DE NEDERLANDEN. door D. BIERENS DE HAAN.

XI. De Logarithmen van Dirk Rembrants van Nierop, J. Wolfram, W.O. Reitz, K.K. Reitz en D. Klinkenberg.

1. In No. I dezer Bouwstoffen hebben wij reeds gezien, dat ezechiel de decker in zijne ‘Nieuwe Telkonst’ eene logarithmentafel heeft gegeven in 8o., eene zoogenaamde kleine tafel; en dat daarop de kleine tafels van adriaan vlack, met al haar verschillende herdrukken, zijn gevolgd. De eerste Hollandsche logarithmentafel, die wij daarna ontmoeten, is eene van dirk rembrants van nierop. Reeds uit dien hoofde zoude zij onze aandacht verdienen, maar ook wegens andere redenen is zulks het geval.

Dirk rembrantsz. van nierop werd in 1610 te Nierop geboren, en overleed aldaar 4 November 1682; hij was schoen-maker van beroep, maar heeft vele werken geschreven over sterre- en zeevaartkunde; en in die richting zullen wij hem later nog wel ontmoeten. Hier hebben wij alleen te maken met zijne ‘Logarithmus Tafelen van Sinus, Tangens en Secants1), in 1671, in 8o.’ uitgekomen. Op den titel leest men dat deze tafels ‘op nieuws uitgewerkt’ zijn door rembrants van nierop: in verso van den titel vindt men zijn ‘Aen den Leser’, waarin hij verhaalt, wat tot deze uitgave aanleiding heeft gegeven.

‘Dese Tafelen zijn volgens de Copye van Ezechiel || de Decker, op 't aangeven van zeker reeken- || meester, gedrukt, die zijn voornemen was, om hier || een onderwijs, met eenige voorbeelden, op te maken: || doch de saeke aldus niet uytvallende, om oorsake van || de kortheyt van 's menschen leven, zo ist dat ik om || dese reden hier toe versocht zijnde, het niet hebben kon- || nen laeten, om dit zelfde by der handt te nemen, || waar in dat ick de beginselen der klootsche driehoeken, || om uyt te werken (mijns oordeels) heel klaer en be- || scheydelijk hebbe voorgestelt, altoos zo veel alst op || dese tijt heeft willen gevallen. Waar mee wenschen- || de dat dit by veele mochte aengenaem zijn, ende haer || in desen oeffenende tot beter voortgank (als voor desen) || mochten geraeken. Desen aldus gerecommandeert la- || tende voor alle liefhebberen dezer konst, maeke dit tot || een eynde, in 't jaer na Christi geboorte, 1671. doen || de sonne noch weynigh treden in de ram gedaen had- || de: en hier mee hope te zijn en te blijven UE. dienst- || willige || dirk rembrantsz.’

Het blijkt dus, dat de tafels van de decker van 1626, niet de betere van vlack, tot grondslag hebben gediend; deze tafel geeft dan ook zes decimalen Het is wel eenigszins bevreemdend, hier op eens, bijna eene halve eeuw later, die tafels van de decker te zien opdagen uit de bijna volmaakte vergetelheid, waarin zij begraven schenen: wij zagen toch vroeger in de nummers I en III dezer Bouwstoffen, dat men ze na de uitgave niet meer vermeld zag. Nu schijnt het aan den anderen kant te blijken, dat dit boekje het eerst was opgezet door een frieschen wiskundige, - althans de drukplaats Harlingen geeft aanleiding tot dit vermoeden. Wie die wiskundige, - naar het schijnt, voor 1671 overleden, - eigenlijk is geweest, is misschien moeijelijk na te gaan. Doch zou men uit deze feiten, te zamen in verband beschouwd, misschien mogen opmaken, dat in Friesland, waar immer de wiskundige wetenschappen met groote voorliefde werden behandeld, het boekje van de decker meer opgang heeft gemaakt, dan wel in Holland? Maar, hoe dit ook zij, onze rembrantsz schijnt veel met de decker te hebben opgehad, en diens meeningen gereedelijk te hebben onderschreven.

Zoo verklaart hij in de ‘Eygenschap dezer Tafelen’ (bladz. 1, 2),

wat ‘Logarithmus of reekentallen’ zijn, hoe men daarmede ‘alle regel van dryen kan uytwerken,’ en laat daarop volgen, bijna evenals de decker zegt,

Het is wel zo/ datter ook Logarithmus ge- || tallen gestelt worden/.... om daer mee.... jae alle regulen van dryen (den koop- || manschap aengaende) kan uytwerken/ ,maer || dit zo veel gereeder niet zijnde/ als wel de || gemeene manier/ daerom dat wy die laeten || varen/ en besien wat men hier meer in kloot- || sche driehoeken kan uytrechten/’

Daarop gaat hij dan ook over tot ‘Verscheyden voorvallen op de kloot- || se driehoeken,’ met hare toepassing op enkele ‘Astronomische Voorbeelden’: bladz. 2 tot 25 behandelt hij ‘de klootse driehoecken/ welcke in rechte || hoeken voorvallen/’ en bladz. 25 tot 36 de ‘Scheeve Klootsche Driehoeken’ van ieder ‘vijfderlye voorvallen’, daar hij het geval, dat alleen hoeken bekend zijn, niet behandelt. Op de volgende bladzijde, in zijn ‘Besluyt’ zegt hij.

‘Doch in || gevalle iemant meer van klootsche reekenin- || gen begeerde...., die besie A. Metius in zijn ‘Astrolabi Catho- || licum2), Mr. Pieter Wils in zijn wiskonstige wer- || ken3), als ook in mijn Wiskonstige Reekeninge4). En || boven dese noch verhope dat haest uytkomen || zal, de klootsche reekeningen van Mr. Gerrit || E. Backer, in zijn leven Schoolmeester tot || Graft, waer in dat alle reekeningen van kloot- || sche werkstucken die tot noch toe, en meer || andere die noch noyt in 't openbaar geweest || zijn, die sullen daer alle klaer en onderschey- || delijck beschreven worden. || Eynde.’

De drie eerst aangehaalde werken zijn bekend. Alleen is hier het volgende op te merken. Uit bladz. 24 van het laatste werk blijkt, dat er in 1656 te Amsterdam een herdruk verschenen is van de Logarithmen van edmund wingate.

Wat den arbeid van g.e. backer betreft, men vindt wel bij de ‘Regula Cos of Algebra’ van j.r. brasser5) te Amsterdam in 1663 uitgekomen ‘Eenige Exempelen van gerrit evertsz. backer, schoolmeester tot Gracht’ bijgevoegd, maar deze handelen niet over bolvormige driehoeken. Van deze ‘Regula Cos’ met de ‘Exempelen’ bestaat wel een tweeden druk van 16726), waarin men dus het door rembrantsz bedoelde werk, zoude

kunnen zoeken; maar deze herdruk is aan de eerste gelijk, en bevat dus het bedoelde niet: dit is mij trouwens ook nergens voorgekomen.

Na dit voorwerk bevat ons boekje de logarithmen. Er gaat geen titel vooraf; de tafels beginnen in verso van het voormelde ‘Besluyt.’

De vier kolommen op iedere bladzijde hebben tot hoofd

(het aantal graden). Sinus. Tangens. Secans.

hoewel het eigenlijk moest zijn Log. sinus, enz. Op iedere bladzijde komen dertig regels voor, geldende voor 0 tot 30 of voor 31 tot 60 minuten. Twee opeenvolgende linksche bladzijden behooren dus tot denzelfden graad: de overeenkomstige rechtsche bladzijden behooren tot het complement, en bevatte dus eigenlijk de Log. Cos., Log. Cotang en Log. Cosecans.

Deze tafels zijn dus werkelijk even zoo ingericht, als de vroeger vermelde van ezechiel de decker.

2. Ruim eene eeuw later ontmoetten wij op het terrein der logarithmotechnie den wiskundige adolf frederic marci, zie No. VI dezer Bouwstoffen: tevens zagen wij aldaar, hoe deze zich verdienstelijk had gemaakt in het zamenstellen van eene tafel der priemgetallen. Omstreeks denzelfden tijd vinden wij een anderen naam, dien van j. wolfram. Deze was een Nederlandsch officier en hield zich met wiskundige berekeningen bezig: hij bewoog zich in dezelfde dubbele richting als de genoemde marci, dat is, hij vervaardigde een uitgebreide tafel van priemgetallen, en berekende een nieuw stel hyperbolische logarithmen; met dezen laatsten arbeid oogstte hij wel den meesten roem in.

Zijne ‘Proeve van eene tafel ter ontledinge der getallen’7) verscheen in de Verhandelingen der Hollandsche Maatschappij te Haarlem. Zij bevat het ‘21ste Deel || van een grooter, in welke de || getallen van 1 tot 126000 ontleed zyn. || Dan in deeze proeve bevinden zig alleen || de Primo-getallen onder 6000, en van || de Gecomponeerde die, welker klein- || ste factor ten minsten 7 is: by gevolg || zyn de getallen, die in 2, 5 en 3 op- || gaan, daar van uitgesloten.’

Deze tafel heeft 22 verticale kolommen: de twee eerste kolommen bevatten de 80 getallen in de eerste 300, die aan bo-

vengemeld vereischte voldoen, namelijk de veelvouden van dertig, vermeerderd met 1, 7, 11, 13, 17, 19, 23, 29. Voor het gemak zijn zij in drie vakken verdeeld: A bevat de 26 getallen in het eerste honderdtal, B de 28 in het tweede, C de 26 in het derde. De volgende kolommen hebben tot hoofd 0, 3, 6, 9, 12, ... 57, die de honderdtallen aangeven, welke bij de getallen der eerste kolom moeten worden bijgeteld. Op die wijze verkrijgt hij een tafel met dubbelen ingang voor al de bedoelde getallen beneden 6000. Is nu het getal een priemgetal, zoo bevat de overeen komstige plaats, niets; anders den kleinsten deeler: dus in deze tafel: 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, en wel respective 229, 124, 95, 67, 57, 47, 37, 32, 28, 22, 22, 17, 15, 10, 8, 6, 4, 2 maal. De belofte, dat ‘Deeze Tafels van 1 tot 126000 zullen in het || eerstvolgende Deel worden meêgedeeld’ is niet vervuld, misschien wel ten gevolge van de uitgave der tafelen van Prim-getallen door a.f. marci, waarover in No. VI dezer Bouwstoffen sprake was.

3. Zijn grooter en belangrijker arbeid is opgenomen in de ‘Neue und erweiterte Sammlung unentbehrlicher Tafeln8) van johan carl schulze’ in 1778 te Berlin in twee deelen uitgekomen. Schulze zegt daaromtrent in zijn ‘Kurze Einleitung zum ersten Bande’ op de vierde bladzijde (zonder pagineering).

‘Die Tafel der natürlichen oder || hyperbolischen Logarithmen bis auf || 48 Decimalstellen ist, ein so wich- || tiges Geschenk für die Integralrech- || nung, dass sie gewis dem Herrn || Wolfram, Artillerielieutenant in Dien- || sten Ihro Hochmögenden der Her- || ren Generalstaaten der vereinig- || ten Niederlande, jetzt zu Nimwegen || befindlich, welcher dieselbe mit der || grössten Sorgfalt berechnet und nach- || gesehen hat, in spätesten Andenken || erhalten und unvergesslich machen || wird. Sie ist die Frucht einer sechs- || jährigen höchst mühsamen und be- || schwerlichen Arbeit, und geht von 1 || bis 2200 für alle Zahlen fort, von || 2200 bis 10000 ist sie hingegen nur || für die Prim- und etwas stark com- || ponirte Zahlen berechnet, weil das || Uebrige durch leichtes Addiren kann || gefunden werden.’

Wel is waar moge de naam van wolfram niet algemeen

bekend zijn, althans veel minder, dan hij wel verdienen zoude: straks zullen wij zien, dat zijn arbeid in Duitschland wel op prijs werd gesteld. Schulze, die blijkens de ‘Kurze Einleitung zum zweyten Bande’ met wolfram over de inrichting van den geheelen bundel heeft gehandeld, laat daarop volgen.

‘Auf der 258sten || Seite, als der letzten dieser Ta- || fel, kommen einige Zahlen vor, bey || welchen die Logarithmen fehlen, und || der Raum weiss gelassen worden. Die- || ses sind entweder Prim- oder sehr || componirte Zahlen, so mit zu den || 10000 gehören. Da Herr Wolfram || vorm Schlusse dieses Werkes wegen || ausgestandener Krankheit die Logarith- || men nicht hat berechnen können, sie || aber nächstens zu completiren geden- || ket, so ist der Raum offen gelassen || worden, um ihm nach Gefallen aus- || zufüllen. Ferner trift man auf der || 259 Seite für die Zahlen der offen ge- || lassenenen (sic) Stellen sowohl als für eini- || ge andere, deren Logarithmen Herr || Wolfram nur einmal hat berechnen || können, und welche daher nicht so || zuverlässig als die übrigen sind, die || zum wenigsten auf zwo verschiedene || Arten sind berechnet worden, die ge- || wöhnliche oder briggische Logarith- || men bis auf 42 Decimal-stellen berech- || net, an.’

Ten opzichte van het ontbreken dezer logarithmen door eene ziekte van wolfram, zien wij verder uit ‘de Einleitung van den Thesaurus Logarithmorum Completus’9) van georg vega in 1794 niets meer, dan hetgeen op blz. XXIX te lezen is.

‘Die letzte Tafel dieses Werkes, welche die von Herrn || Wolfram, einem holländischen Artillerie-Officier, berech- || neten natürlichen Logarithmen mit 48 Decimalziffern ent- || hält, ist aus der Sammlung der logarithm. trigon. Tafeln || des Herrn J.C. Schulze, Berlin 1778. mit Ergänzung der || daselbst abgängigen Stellen und Berichtigung einiger über- || sehenen Fehler abgedruckt.’

Maar ik meen ergens gelezen te hebben, dat deze aanvulling der door wolfram eerst overgelaten leemten door van vega zelven is geleverd: als dat waar is, zoude daaruit volgen, dat wolfram die niet heeft bewerkt, althans niet heeft in het licht gegeven. Misschien wel is hij bezweken aan de ziekte, die hem belette zijn arbeid volledig te maken voor de tafels van schulze.

4. Doch ook andere Hollanders gaven omstreeks dienzelfden tijd beschouwingen over het berekenen van Logarithmentafels.

De eerste was wilhelm otto reitz, Lector Juris en Rector te Middelburg, geboren den 20sten Juli 1702 te Offenbusch en overleden 22 October 1768 te Middelburg (zooals blijkt uit de Verhandelingen van het Zeeuwsch Genootschap, Dl. I, blz. XLIV): hij was pas den 26sten Juli 1768 lid van dat genootschap geworden. Deze gaf in 1754 zijne ‘Nieuw gevonde berekening der kunstbreuken’10), verdeeld in drie afdeelingen. In de eerste behandelt hij de regels voor de kunstbreuken, dat is de logarithmen van gewone brenken, die hij uitdrukt door de letter f, ‘die het teeken van een fractio of breuktal is’; bijv. den logarithmus van 0,000683 schrijft hij 4 f 0.8344207, zooals wij zouden schrijven 0.8344207-4. De ‘Tweede Afdeeling. || Behelzende een lichten en algemeenen Regel || om, zoo wel de Somme, als Overschot || van twee Kunsttallen te berekenen,’ geeft eerst een zeer zamengestelden regel van josef muschel de moschau uit de Acta Eruditorum van 1696; daarna zijn eigen zeer eenvoudigen regel, om te vinden Log. (a±b) als Log. a en Log. b gegeven zijn. De methode in de ‘Derde Afdeeling. || Lichte en gewisse manier om groote Breuk- || tallen of Proportiën tot kleinder te bren- || gen, die voor ket gebruik veel bekwa- || mer en nochtans voldoende zyn’ berust op de theorie der gedurige breuken. Ten slotte een ‘Toegift || van een kunstgreep, om een gegeven getal te || toetsen, of het door 11 juist deelbaar zij.’

In het volgende jaar verscheen zijn ‘Berekening van Kunsttallen’11), waarin hij eerst eenige regels geeft van logarithmotechnie, en ook onder andere een regel voor benaderd deelen; en daarop eene tafel der logarithmen voor de getallen 1-1000 (blz. 184-209) met hare eerste differentiën; vervolgens eene ‘Tweede Tafel’ van de Logarithmen van 1 + a. 10-n, voor a = 1 tot 9, n = 3 tot 18 (blz. 210-212), waarbij voor n = 3 tot 10 de eerste differentiën zijn gevoegd. Alle logarithmen zijn tot in 18 decimalen berekend.

Aan het slot beloofde hij een onderzoek te zullen uitgeven, dat in 1757 verscheen onder den titel ‘Nieuwe bespiegeling en Ontcijfering der teerlingsche vergelijkingen’12), waarin hij

(blz. 279-285) een ‘Tafel van Teerlingsche vergelykingen’ geeft. Voor alle wortels z = 0,01 tot 2,00 berekende hij voor de vergelijkingen z3 - z = AE, of z3 + z = AE, de waarden van AE (= Aequatio) in zes decimalen. In een ‘Nabericht’ bespreekt hij de methode van clairaut in zijne ‘Elemens d'Algèbre.’

Tien jaren later kwam in het licht zijne ‘Nieuwe oplossing der stelkundige vergelijkingen van de vierde macht, en hierdoor ook van de derde macht’13). Hij tracht hierin de herleide vergelijking van de vierde macht x4 + axx + bx + c = 0 aldus te vervormen. (x3 + p)2 = (qx + r)2.

Als ‘Aanhangsel’ geeft hij de oplossing van een vraagstuk omtrent de middellijn van Venus, bij haar Loop voorbij de Zon.

Zijne volgende verhandeling ‘Nieuwe bespiegeling der klootsche figuren, Met de Berekening van derzelver oppervlakte of inhoud’,14) uitgegeven als ‘volkomen nieu, || en van myne uitvinding,... door mynen goeden vriend den Wis- || kunstenaar laur. dunewey de munck, || aangemoedigd’, levert eenige stellingen omtrent bolvormige figuren, en wordt gevolgd door een ‘Byvoegsel omtrent de toover-vierkanten || van effe getallen.’ Deze waren geconstrueerd door zijnen ‘Broeder, karel koenraad || reitz, Hoogleeraar te Harderwijk.

Eindelijk heeft men nog zijn ‘Grondig onderwijs in de behandeling der breuktallen, zoo gemeene als decimale of tientallige, benevens de daarafhangende rekeningen’15) in 1769, als opus posthumum uitgegeven. Men vindt daarin de behandeling der gewone en tiendeelige breuken, omdat ‘noch geenerlei grondig on- || derwijs der decimale of tiental- || lige rekeningen, en wat 'er ver- || der toe behoort of van afhangt, in 't Neder- || duitsch uitgegeven zy.’ Onder anderen het ‘IV. Hoofdstuk. || behelzende de tiendetafels || met derzelver gebruik’ (blz 343-351) dat is, herleidingstafels van maten, gewichten, enz. in tiendeelige breuken.

5. De arbeid over logarithmotechnie werd voortgezet door Mr. karell koenraad reitz: niet den broeder van den voornoemden, Hoogleeraar te Harderwijk, (geb. in 1708 en overleden 13 September 1773), maar den zoon van w.o. reitz: hij was

Griffier van den Haad van Vlaanderen, te Middelburg. In 1769 kwam uit zijne ‘Nieuwe Handleiding om den Logarithmus voor eenig gegeven getal naaukeurig te vinden tot veertien letteren boven den index’16), waarin hij het gebruik der tweede verschillen verklaart bij het berekenen van logarithmen, en deze aanwendt voor zijne ‘Tafel || der Kunsttallen of Logarithmi || voor de natuurlyke getallen || van 1000000-1001000. || berekend || tot XV. letteren boven de || merkletter of index’ (blz. 455-480), waarin volgens de oudere methode de eerste verschillen tusschen de opeenvolgende logarithmen zijn geplaatst. In dit stuk belooft hij een vervolg: en dit verscheen in 1790 onder den titel ‘Aanhangsel tot de nieuwe handleiding om den Logarithmus voor eenig gegeven getal naaukeurig te vinden tot veertien letteren boven den index’17), waarin hij ook van de derde verschillen gebruik maakt, en deze leert aanwenden bij de logarithmotechnie.

6. Tusschen deze beide mannen, ontmoeten wij nog den naam van dirk klinkenberg, geboren den 15den November 1709 te Haarlem, en op het einde van April 1799 te 's Hage overleden, Ordinaris Klerk ter Secretarye van Holland, en wel in zijne ‘Korte verhandeling over de Sinus, Tangens, en Secans Logarithmus getallen’18), waarin hij eerst de berekening dier logarithmen behandelt en daarna (bladz. 291-307) de ‘tafelen, || tot gebruik van de || sinus, tangens, || en || secans logarithmen, || in de gedeeltens van mi- || nuten graads’ geeft. Deze bevatten voor iedere minnut der acht eerste graden dus voor 1-480 minuten de Log. Sinus en Log. Tangens in zeven decimalen met de verschillen. Daarop volgt (bladz. 308-310) een ‘Tafel, dienende om te Corrigeeren de Sinus, || Tangens, en Secans Logarithmus, op Dui- || zendste deelen van Minuten Graads.’

Dezelfde klinkenberg was niet alleen in de wiskunde zelve, maar ook in de sterrekunde ervaren, zooals blijkt uit zijne onderscheidene verhandelingen.

In 1755 gaf hij eerst een ‘Kort berigt wegens eene Comeetsterre, die zich in den Jaare 1757 (1758), Volgens het Systema van newton, halley en andere Sterrekundigen, zal vertoonen’19); waarin hij eene voorloopige berekening der loopbaan

leverde, en daaroj eene ‘Beschouwing over de Deelen van het Bastion, Volgens een daarover opgegeven Voorstel, van den Hooggel: Heere n. ypé, Hoogleeraar in de Wiskunde te Franeker’20), waarin hij twee tafels leverde voor de centerhoeken van 90 tot 0 graden voor elken graad, met de titels: ‘I Tafel, van de grooten der Hoeken, en langten der Lynen van het Bastion, enz. || zynde de Langte der Defens-linien AD gelyk BL, op 60, en de Facen AF gelyk BZ, || bestendig op het derde deel van dien, naamelyk 20. Roeden genomen. || De nommers, agter de Roeden, zyn Decimaal fractien,’ en vervolgens ‘II. Tafel, de hoeken blyven eeven gelyk als in || de I. Tafel, maar de langten der Lynen, zyn || in zulke Deelen, en decimaal fractien uitge- || drukt, waar van de buiten Polygone AB, || bestendig 100. deelen is.’

In 1755 ontmoeten wij eerst zijne ‘Verhandeling over de evenredigheid (of reden) tusschen de Middellyn en tusschen den omtrek van een Cirkel’21), waarin hij de berekening door reeksen behandelt. Hij zegt daar (bladz. 155):

‘derhalve zal de reex ||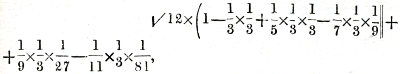 illustratie enz de lang- || te van de geheele omtrek der Cirkel uit- || drukken, den Diameter gelyk 1 zynde,’ en geeft dan de berekening tot 21 decimalen, ‘op dat blyke, met hoe weinig || moeite men door deezen weg tot zo ver- || re kan komen, als waar toe Mr. l. van || ceulen het zelve door een grooten || en roemwaardigen arbeid gebragt heeft.’ (blz. 156).

Hieruit zoude blijken, dat klinkenberg, vreemd genoeg, niet bekend was met den naderen arbeid van ludolf van ceulen (waarvan in het No. VIII dezer Bouwstoffen gesproken is): en dit wordt bevestigd door hetgeen hij reeds op bladz. 149 had gezegd.

‘Daar l. van || ceulen zig vergenoegd had, met zulks || tot twintig of één en twintig Numero's || te brengen.’

Op dit stuk volgden in ditzelfde jaar zijne ‘Verhandeling over de Pegelkunde, zo als dezelve tot grooter volmaaktheid gebragt word door de Fluxie-rekeningen’22), waar hij de for-

mule gebruikte 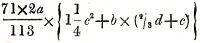illustratie zijn ‘Vraagstuk, de zee-vaart-kunde betreffende’23), in het vorige jaar door johnson in Engeland opgegeven; - dan ‘Over een meetkundig werkstuk’24) betreffende eene zekere grootste waarde of maximum; - eindelijk zijne ‘Afbeeldinge der Eclipsen, op eene Nieuwe Wijze voorgesteld’25), waarin twee maan-eclipsen worden geconstrueerd.

Reeds in 174326) had klinkenberg gewezen op de gelegenheid ter bepaling van den afstand tusschen zon en aarde bij den overgang van Venus voorbij de zon in 1761: en deze arbeid was in de geleerde wereld met belangstelling ontvangen. Toen dus die overgang naderde, schreef klinkenberg den 12den November 1760, eerst zijne ‘Verhandeling, beneffens de naauwkeurige algemeene en byzondere Afbeeldingen van den overgang der planeet Venus voorby de zon, op den 6 Juny 1761 des morgens’27) en daarop in 1761 zijne ‘Verhandeling en Aanmerkingen over verscheide uitrekeningen, en waarnemingen van den overgang van Venus voorby de zon; op den 6den Juny 1761’28) met het ‘Nabericht, behoorende tot die Verhandeling’29), waarin hij eene discussie levert van de waarnemingen tijdens dien overgang.

Wij zagen reeds in zijne verhandeling van Noot (19), hoe hij zich met de waarneming van kometen bezig hield: deze arbeid was de aanleiding tot zijne benoeming als correspondent van de Fransche Akademie van Wetenschappen te Parijs. Ook sedert heeft hij zich veel met zulke waarnemingen bezig gehouden, zooals blijkt uit zijne verhandelingen ‘Observations on the late Comet in September and October 1757’30), geplaatst in de Philosophical Transactions van 1758, en ‘Observations de la Comète de 1759’31), opgenomen in de Memoires de l'Académie Royale des Sciences te Parijs, van 1760. Bijna een vierde eeuw later was het klinkenberg, die het eerst bewees dat de nieuwe ster Uranus geen komeet was, in zijne ‘Verhandeling over eene kleine doch ongewoone sterre, dewelke het allereerst in Engeland is ontdekt in de maand Maart 1781’32); men vindt ze in het zevende Deel der Verhandelingen van het Bataafsch Genootschap van 1783.

Nog heeft dezelfde wiskundige medegewerkt tot de Rivierkundige stellingen’ van hetzelfde Bataafsch Genootschap te Rotterdam: tot dit onderwerp behooren zijne ‘Nader elucidatie over een poinct van Aanmerking op de achtste en volgende stellingen’33) en zijne ‘Aanmerkingen over de nader Elucidatie’34) te vinden in het eerste en tweede deel der Verhandelingen van genoemd genootschap.


Vorige Volgende

Over dit hoofdstuk/artikel

auteurs