Bouwstoffen voor de geschiedenis der wis- en natuurkundige wetenschappen in de Nederlanden
(1878)–David Bierens de Haan–
[pagina 99]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
BOUWSTOFFEN VOOR DE GESCHIEDENIS der WIS- EN NATUURKUNDIGE WETENSCHAPPEN IN DE NEDERLANDEN. door D. BIERENS DE HAAN. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VII. Simon van der Eycke.1. In het laatste gedeelte der zestiende eeuw, ontstond er in de mathematische wereld, hetgeen men zoude kunnen noemen: eene epidemie van cirkelquadraturen, dat wil zeggen van of geheel valsche, of werkelijk benaderende bepalingen van de verhouding van den omtrek tot de middellijn des cirkels. In den regel echter waren de grondslagen deze bepalingen niet zuiver, de afleiding zelve weinig wetenschappelijk. Ook ons land bleef niet vrij van deze besmetting. En wanneer het mijn voornemen is, daarover het een en ander onderzoek mede te deelen, zal het wel noodig zijn, om deze opstellen met eenige woorden te rechtvaardigen. Daartoe zij het echter genoeg er op te wijzen, vooreerst, dat het in die dagen juist de bekende geleerden waren, die zulks beproefden; ten anderen en voornamelijk, dat de strijd daartegen door de wiskundigen van naam werd aanvaard, en veelal aanleiding gaf tot soms groote vorderingen op wetenschappelijk gebied. Iedere zoodanige cirkelquadratuur werd op die wijze, laat ons zeggen haars ondanks, een vuurwerk in de wetenschap, dat zijn licht deed schijnen over de mannen, die zich toen ter tijde aan hare beoefening wijdden, en over de wijze en de methoden, waarop toen die wetenschap werd be- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 100]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
oefend. Of ook, zulk eene cirkelquadratuur werd een middelpunt, waaruit onderscheidene belangrijke geschriften en ontdekkingen ontsprongen langs allerhande verschillende wegen. De eerste van zoodanige proeven, waarmede wij hier willen aanvangen, is die van simon van der eycke. 2. Deze simon van der eycke werd ook wel genoemd (en noemde zich zelven ook wel, naar de gewoonte dier dagen) simon à quercu, simon du chesne, soms eenvoudig duchesne. Van zijn levensloop is slechts weinig bekend. Wij zullen zien, dat hij in 1584 te Delft woonde, en dat hij in 1603 nog leefde. Hij was geboren te Dôles; maar was toch meer nederlander dan franschman, althans naar zijn stijl van schrijven te oordeelen. Zijn schrijven in het fransch is dikwerf niets beter dan woordelijk vertaald hollandsch; zooals wij straks meermalen de gelegenheid zullen hebben op te merken. Waarschijnlijk was zijne familie wegens hare godsdienstige gevoelens naar ons land gevlucht: men zegt althans, dat hij een streng calvinist is geweest. Trouwens in de voorreden van zijn straks te behandelen werk ‘Quadrature du cercle’ zegt hij, sprekende van al het-geen Prins willem I. deed en leed, ‘à l'imita- || tion d'icelluy mesme, pour la parole duquel exposez jours || & nuicts vostre personne en infinitz d'angers, (sic)’ en aan het einde dier voorrede spreekt hij van ‘son Eglise affligiée.’ Terwijl hij dit werk zelf eindigt met de woorden: ‘Rendant graces & louanges à l'Eternel, duquel toutes || choses procedent, & auquel toutes choses sont finalement || reuocquèes, Par Jesus-Christ son Filz vnic- || que nostre saulueur et redempteur || auec son sainct Esprit. || Amen.’ 3. Uit deze weinige bijzonderheden blijkt echter, dat hij niet verward moet worden met zijnen naamgenoot simon van der eycke, ook wel genoemd simon brabant à, quercu: hoezeer het zeer wel mogelijk is, dat zij bloedverwanten waren. Deze was te Brussel geboren, werd zanger aan de St. Stephanskerk te Wien, en daarna kapelmeester bij ludovicus sforza, Hertog van Milan tot aan 1508; waarna hij dezelfde betrekking bleef bekleeden onder diens z'oon maximilianus. Hij schreef toen een bekend werk over de muzijk ‘Opusculum Musices de Gregoriana et Figurativa et Contrapuncto Simplici, cum Exemplis. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 101]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Viennae, 1509 in 4o’; waarvan er een tweede druk verscheen in 1518 te Dandshut in 8o. 4. Onze simon van der eycke behoorde tot de eersten, die zich bezighielden met het vraagstuk ‘van de Oost- en West-vindinge,’ zooals het toenmaals heette, dat is van het bepalen der lengte op zee. Dit blijkt uit eene vrij belangrijke Resolutie van de staten van Holland, gedateerd 12 September 1595Ga naar eind1): waartoe het verzoek om een privilegie, dat van der eycke had ingezonden, aanleiding gaf. De mededingers schijnen geweest te zijn plancius, sieuwertsz en p.r. twisk, mannen, wier naam in de geschiedenis der wetenschappen niet onbekend is. Uit de bewoordingen en de voorwaarden, die in deze Resolutie voorkomen, blijkt genoegzaam, welk belang men reeds toen ter tijde in dit vraagstuk stelde; dat men voor de goede oplossing bereid was ‘eene eerlycke recompence te geven, sulcks dat hij ende de sijnen hun daarmede sullen genoegen ende contenteren.’ Het was derhalve van belang te achten, de noodige voorzorgen te nemen en de noodzakelijke voorwaarden te stellen, ten einde later verschil van gevoelen met de gevolgen van dien te voorkomen: en het nemen van zulke voorzorgsmaatregelen was aan onze voorvaders best toevertrouwd. Later in 1608 ontving onze simon van der eycke nog een octrooiGa naar eind2) voor de nieuwe uitvinding van een molen. 5. Thans komen wij tot zijne cirkelquadratuur ‘Qvadratvre dv cercle’Ga naar eind3), die in 1584 te Delft het licht zag. De opdracht luidt aldus. ‘A treshavlt et || tresillvstre seignevr || Gvillavme Prince d'Oranges, || Comte de Nassauvve, Catzenelleboghen, Dietz, Via- || nen, Buren, Leerdam, &c. Seigneur & Baron de Breda, || Diest, Grimbergen, Arley, Noseroy, Chastelbellain &c. || Vicecomte d'Anuers & Besançon, Gouverneur & Ca- || pitaine general d'Hollande, Zéelande, Frize & Vtrecht.’ Hij zegt daarin ‘Si suis je poulcé comme d'vn par- || ticulier debuoir à telle recognoissance, pour auoir entendu || S. Ex. n'estre seullement amateur des sciences Mathematic- || ques, mais en auoir aussi plaine cognoissance.’ En eindigt met de woorden | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 102]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
‘Lequel Dieu tout || puissant je prie de tout mon coeur, qu'il luy plaise par sa bon- || té immense, vous dōner repoz, de tant de trauaulx, que pour || l'amour de sa foy, auez soubstenu & encore soubstenez, vous || maintenant en santé entiere & longne (sic) vie, à l'edification de || son Eglise affligiée, & au bien de touts ceux qui vous ay- || ment. En Delff ce 28. de Januier, 1584. || De S. Ex. || Treshumble Seruileur || Simon du Chesne.’ Dit zeldzame boekje is in drie boeken of ‘Parties’ verdeeld, die wij kortelijk willen nagaan. Het eerste heet ‘Premiere partie || de ce traicte, ov est de- || monstre, qv'il ne pevt estre, || que la circumference du cercle n'aye raison à son || Diametre’. Hij begint aldus. ‘Combienqve quelques vns ont affirmé, le cercle || se pouuoir mettre en parfaicte quarrure, entre les- || quels est Aristote. lequel dict que ce qu'est egual a vne || figure rectiligne se peut quarrer ou mettre en quarru- || re: si est ce que d'autres le nyant ont osé diré (sic) qu'il est impossible, qui In- || terroguez pourquoy? ont respondu, pource que la circumference du cercle || n'a aucune raison à son diametre, & ce à cause que le droict & le cour- || be ne sont pas d'vn mesme genre de quantité. Mais de ce a Jan du Mont || royal assez bien faict apparoistre le contraire, disant que toutes lignes || ont vn mesme commencement de leur generation, assauoir le poinct, selon || le mouuemēt imaginatif duquel, les mathematiciens affirment les lignes || naystre... || pour confirmation de quoy, nous auons beaucoup de tesmoignages de plu- || sieurs geometres. N'est il pas ainsi (dit il) que Archimede voulant de- || monstrer au commencement du premier liure de la sphere & du cilin- || dre, la somme des costez du poligone circumscript au cercle, estre plus || grande que la circumference du cercle mesme auquel il est circumscript, || ... || certes elles ne se pourroient dire plus grandes, si elles n'estoient || de mesme genre de quantité: car il n'y auroit autrement raison aucune || entre icelles & l'arc du cercle... || ... || D'ou || appert clerement qu'Archemide (sic) a esté d'oppinion, que le droict & le || courbe sont d'vn mesme genre de quantité. D'advantage Ptolemée vou- || lant au septiesme chapitre du sixieme liure de sa grande compilation, des || doigts eclipticques lineaires, extraire les doigts superficiels, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 103]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a, à l'imi- || tation d'Archimede prouué, la raison de la circumference du cercle à son || diametre, estre enclose entre deux raisons cogneūes (sic)... || ... || Mais telles choses sont aussi presupposées au liure des trois || freres, ou est proposé à demonstrer, que les circumferences de touts cer- || cles ont vne mesme raison à leurs diametres... || ... || D'ou on se || peut de ceux esmerueiller, qui disent le courbe & le droict ne pas estre || de mesme genre: car à vray dire, estre courbe ou droict sont choses, les- || quelles ne pouuant changer le genre, causent seulement telles passions || aux quantitez, &c.’ || Dit alles dient als inleiding tot de bestrijding van het gevoelen van michiel stiffel. ‘Ce non obstant s'efforce michiel stiffel en son Arithmeticque Latine, || à demonstrer, que la circumference du cercle n'a aucune raison à son dia- || metre, cest à dire ne discibleGa naar voetnoot*), n'indiscible, disant: || 1. Il faut a quiconque veut disputer de la quadrature du cercle, faire || distinction entre le cercle mathematicque & le cercle phisicque. || 2. Il luy conuient aussi d'obseruer, que la question meüe entre les Phi- || losophes est du cercle mathematicque, & non du cercle phisicque. || 3. Le cercle phisicque est vne jmage du cercle mathematicque.’ Op deze drie volgen nog vijf en twintig andere sluitredenen van stiffel, waarvan de drie laatsten zijn. ‘26. Et s'ensuyt tiercement, qu'il est impossible de quarrer le || cercle mathematicque. || 27. Pour peu sçauants soient ceux tenuz qui vouldront s'opposer à || ces choses, qui sont telles, qu'elles ne donnent ny n'ostent a la pieté. || 28. Toutesfois les doctes sentiront auec moy, Euclide & Ptolomée || en auoir jugé le mesme.’ En op deze redeneering van stiffel laat van der eycke dadelijk volgen. ‘Or puisque ainsi est, que apres en auoir par la grace de Dieu || cogneu ce que s'ensuyura, & que ne voulant cacher le don quil luy || a pleu ne donner. J'ay comme plusieurs aultres qui deuāt moy l'ont || faict, osé mettre en avāt, d'auoir trouué le moyen de quarrer le cer- || cle.’ En nu gaat hij er toe over om stiffel volgens zijne eigene | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 104]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
methode te wederleggen (bladz. 10-35). Hij zegt onder anderen (bladz. 10). ‘Et (pource que comme l'ordre des nombres, ainsi procede aussi l'or- || dre des figures poligones) comme quelqu'vn des nombres est le premier || de touts, mais nul de touts le moyen ou le dernier: ainsi y a il quelque fi- || gure poligone qui de toutes est la premiere, mais nulle qui soit de toutes || la moyenne ou la derniere: Parquoy si on veut que le cercle soit la der- || niere de toutes les figures poligones qui jamais ne s'jmagine, il sera, ce || que pas est & que jamais ne sera jmaginé. || Et pource qu' on ne sçauroit faire distinction entre ce qui n'est pas || & son jmagc, sa distinction sera vaine. || ... || D'advantage, pource que cercle mathematicque n'est pas, & que || ce que n'est point ne peut auoir jmage, le cercle Phisicque ne sera pas. || Mais pource que ce qu'est impossible s'en ensuyuroit, il nese peut faire || que le cercle soit la derniere de toutes les figures poligones, car autre- || ment, estant, il seroit ce que point n'est.’ En op bladz. 12. ‘La figure poligone sera donc || plus petite que le cercle, de laquelle l'vn des costez, sera la ligne droicte || (par la premiere demande) menée d'vn quelconque poinct en la circum- || ference prins, au poinct qui en icelle luy est le plus prochain: Si que vou- || lant que le cercle soit vne figure poligone, il seroit finalement necessaire || que vn chascun de ses costez fust vn poinct: car comme selon telles rai- || sons, il ne pourroit estre plus arand, aussi ne pourroit il estre plus petit, || d'autant que le poinct est indivisible: Et de tout ce s'en ensuyvroit il, || que les terminaisons ou confins de quelque superfice angulaire, seroient || poincts & non lignes, contre la 6e definition dudict premier liure.’ Het aangehaalde moge hier volstaan om de redeneertrant van dit boekje voor oogen te stellen: de sophismen te doen zien, die men toenmaals bezigde, om zijne stelling te bewijzen. Nadat hij op die wijze de redeneering van stiffel weerlegd had, roept hij uit op bladz. 30. ‘Av. reste j'aime beaucoup mieux estre tenu pour peu sçauant, || voire pour du tout ignorant, pour m'estre opposé a ce que sur ce || faict dit Stiffel, que dire avec luy. La circumference du cercle & || son diametre (choses de mesme genre de quātité & | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 105]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
desquelles l'vne || recoipt sa grandeur par la grandeur ou longueur de l'autre) n'auoir || l'vn à l'autre raison aucune, comme si en nature il y auoit deux || choses de mesme genre sans raison l'vne à l'autre.’ Hij eindigt met aan te toonen, dat noch ptolomaeus, noch euclides het met stiffel eens zijn geweest, zooals deze laatste beweerd had. 6. In het tweede boek met den titel: ‘Seconde partie || contenant la demon- || stration de la raison de la || circumference au diametre, selon la vulgaire inuention || d'Archimedes.’ Van der eycke begint aldus. ‘Ayant doncques jusques icy assez faict apparoistre, || qu'il ne peut estre que la circumferēce ne admettre quel- || que nombre, et que pource aussi elle n'aye raison à son || diametre. Je di en oultre, la raison de la circumference || du cercle à son diametre debuoir estre telle qu'est la raison de l'aire du || cercle au quarré du semidiametre du cercle mesme:...|| ... || Et conuersement par le correlaire || de la 4e. proposition du cinquiesme, quelle est la raison de l'aire du cercle || au quarré du semidiametre, telle sera la raison de la circumference au || diametre du cercle mesme. ceque donnons de nostre inuention. Mais || d'autant qu'icelle est enclose entre deux raisons cogneues comme dict || a esté, il faudra consequemment veoir, quelles sont celles raisons entre || lesquelles elle est enclose, sçauoir est selon la vulgaire inuention d'Ar- || chimede & suyuant l'xemple (sic) d'Oronce.’ Daarop berekent hij de omtrekken van een omgeschreven regelmatigen 12hoek, als 12 × 11:42 19/42;, van een 24hoek, als 24 × 11:84⅙, van een 48hoek, als 48 × 11:169, eindelijk uit de ‘costé du mult- || angle ou poligone, ou polipleure de nonante six costez, descrit à l'entour || du cercle donné,’ den omtrek van den 96hoek, als 96 × 11:337 8/13. Daarop laat hij volgen (bladz. 42): ‘Puis donc, que la circumference du || cercle est plus petite, que n'est le circuit du polipleure circumscript, || par plus forte raison la circumference du mesme cercle à son propre dia- || metre obseruera vne raison plus petite que triple sesquiseptiesme, || c'est à dire quelle contiendra trois fois le diametre & peu moins d'vne || septiesme partie d'icelluy diametre: ce qu'il failloit demonstrer.’ En bladz. 43, 44: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 106]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
‘Or que la circumference au diametre du cercle obserue vne raison || plus grande que triple superdecupartiente septante vniesmes: c'est à dire || qu'elle contienne troisfois le diametre & vn peu plus d'vne huictiesme || partie d'celluy, (sic), cela se demonstre ainsi.’ Voor ingeschreven veelhoeken van hetzelfde aantal zijden als boven vindt hij achtervolgens voor den omtrek 12 × 15:58; 24 × 15:115; 48 × 15:229½; 96 × 15: 458½; het laatste op bladz. 50. Nadat hij aldus de verhouding van archimedes bewezen had, wederlegt hij dadelijk daarop (bladz. 51) een bezwaar, dat men verder zoude kunnen maken, aldus. ‘Or me pourra quelcun de l'oppinion de Stiffel en cest endroict || dire, Encore n'y a il, espoir aucun, de trouuer l'indubitable maniere || de quarrer le cercle, pour auoir cogneu la raison de la circumfe- || rence du cercle à son diametre, estre enclose entre ces deux termes || 3 10/71. & 3 10/70. Car il ne s'en ensuit rien d'ainsi argumenter: Il est || possible de trouuer vn quarré plus petit que ce cercle. Et est possible de || trouuer vn quarré plus grand que ce cercle. Et pource aussi de trouuer || vn quarré qui luy soit egual. Tout ainsi qu'il ne s'en ensuyt rien de dire: || Il est possible de trouuer vn nombre discible, moindre que le nombre in- || discibleGa naar voetnoot*) R. 9000.-R 16200000.Ga naar voetnoot†) comme ce nombre discible || suyuant.
Et est possible de trouuer vn nombre discible, plus grand qu icelluy || mesme nombre indiscible R. 9000.-R 16200000. assauoir.
Et pource aussi de trouuer vn nombre discible qui luy soit egual. || Mais je luy Respond, que ceste raison n'a pas lieu en toutes choses. Car || (affin que la verité de ce apparoisse par quelque exemple & ce de no- || stre inuention) si pour ne sçauoir trouuer vn nombre discible egual au || nombre indiscible predict, combien qu'il soit loisible d'en trouuer vn plus || petit & aussi vn plus grand, quelcun vouloit affirmer, qu'il ne s'en en- || suit aussi rien icy, de dire: Il est possible....’ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 107]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
En daarop geeft hij eene meetkundige constructie voor de bovenvermelde wortelgrootheid, waarop hij hier niet verder aandringt, maar die wij later weder zullen ontmoeten. 7. Op bladz. 56-90 volgt nu het derde boek, waarvan het opschrift luidt. ‘Troisiesme et || derniere partie demon- || strant par qvelle maniere || se peut trouuer la ligne droicte, eguale à la circumfe- || renciale ligne du cercle proposé, & descrire le quarré, || equal au mesme cercle donné.’ Hierin gaat van der eycke zijne eigene quadratuur afleiden ‘(& par la bonté immen- || sé (sic) du createur de l'vniuers premier & dernier)’ (bladz. 56). Hij begint even als in het eerste boek bij de wederlegging van michiel stiffel, met het stellen van 39 ‘principes,’ waarvan de laatste luidt. ‘39. || Et pource di je derechef, qu'il y aura raison entre la circumfe- || rence du cercle & son diametre.’ Hierop laat hij volgen (bladz. 65). ‘Ce estant donc premis, d'autant que le cercle est de toutes fi- || gures la plus capace, plus parfaicte & plus simple: auquel toutes- || fois comme aux autres conuient aussi le nombre ternaire (combien || que occultement) à respect du centre, de la circumference, & de || l'interuale. Nous eslirons en premier lieu l'vnité, comme celle qui || à touts nombres est commencement & fin, ayant en second lieu || esgard aux nombres binaire & ternaire (qui selon plusieurs ont || affinité, asçauoir cestuyla avec la matiere à cause de sa diuisibilité en || deux parties eguales, par laquelle il la resemble, & cestuyci auec la for- || me, à cause qu'il est indiuisible en deux parties eguales).’ Nadat hij door middel van veel geconstrueerde lijnen, eindelijk gekomen is tot twee lijnen a p = 484, a m = 1521, zegt hij bladz. 73. ‘Si que par ainsi il nous || sera manifeste, la raison de la ligne droicte ar, au diametre af, || estre telle, que de 3 69/484. à 1. que est moins que 10/70. & plus que || 3 10/71. A raison dequoy, nous pourrons dire, la ligne droicte a r, || estre eguale à la circumference du cercle a f g, proposé à quarrer, || la ligne droicte qui d'icelle mesme est le quart, àsçauoir a m, estre || eguale au quart de la circumference. Et (d'autant que c'est le pro- || pre du costé du quarré egual au cercle) celle qui est trouuée estre || moyenne proportionnelle, entre ladicte ligne droicte a m, & le || diametre a f, (àsçauoir a g,) le costé du quarré egual au cercle.’ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 108]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dit is dus nog slechts eene benadering; maar nu tracht hij uit het ongerijmde te bewijzen, dat deze benadering de werkelijke waarde is. ‘Si non, c'est a dire, si la ligne droicte ar, par les lignes droi- || ctes 1, 2, 3, trouuée, n'est eguale a la circūference, ne son quart || au quart d'icelle, ne par consequent la ligne droicte a g, ou celle || qui luy est eguale (a t,) au coste, du quarré, egual au cercle proposé: || Il faudra necessairement, que ladicte ligne droicte ar, soit plus || grande que la circumference, ou bien quelle soit plus courte qu'icelle. ||’ Het besluit daarop luidt aldus (bladz. 77). ‘Mais que s'aydant finalement desdicts trois nōbres 3. 2. 1, || en la maniere qu'auons faict, ausquels il sera force de s'arrester (à cause || qu'il n'y a rien qui precede l'indiuisible vnité) on trouuera ce que dessus || est trouué, àsçauoir que le diametre faisant 484. il faudra que la circū- || ference vienne à faire 1521. Et ne pourra on pour estre à l'vnité parve- || nu, hors d'iceux autre chose aller cercher.’ Van der eycke gaat vervolgens over tot het bepalen van den inhoud des cirkels, en komt op bladz. 83 tot het volgende besluit. ‘Et par ainsi colligerons nous finalement de ces cho- || ses (moyennant la 15. proposition du cinquiesme liure || d'Euclide,) que pour commodement & sans changer la || predicte raison de 1521. à 484 trouuer le costé du quarré || egual au cercle propose, il fauldra partir le diametre d'icel- || luy en 44. parties entre elles eguales (par la neufuiesme || proposition du sixiesme). Et prendre la piece du diame- || tre qui en contiendra 39. pour le costé du quarré egual au || cercle donné. Et au contraire, que pour trouuer le cercle || egual au quarré proposé. Il fauldra partir le costé d'icelluy en || 39. parties eguales (par la mesme neufuiesme proposition) || & l'ayant continué tant quil en sera besoin (par la 2e. de- || mande) à icelluy adiouster 5 d'icelles parties eguales (par la || 2e. demande & troisiesme proposition du premier) car les || 44. telles parties eguales, feront ensemble le diametre du || cercle egual au quarré proposé.’ En dadelijk hierop laat hij volgen bladz. 84. ‘Mais si de la raison de la circumference du cercle à son diametre, || nous debuons attēdre quelque belle proprieté, que | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 109]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pourriōs nous en icelle || désirer plus admirable fors que (comme aussi par ceste mesme raison il || aduient) selon elle les contenuz de touts cercles dont les diametres sont || rationnaux soyent trouuez estré (sic) nombres quarrez? ce que certes celluy, || eut facillement peu croire debuoir necessairement ainsi advenir qui || qui (sic) bien ayant cogneu & consideré toutes les passions ou conditions du || cercle & du quarré les eut ensemble conferé... || ... ||. Il ne veux ja dire, par les autres proprietez au cercle & au || quarré communes: Ou par les dignitez de plusieurs aux quarrez || attribuées, Nommement des Pythagoriens, qui de la disposition || des nombres de c'este table, monstrent les quarrez totalement imi- || terGa naar voetnoot*) les ver- || tus, à cau- || se qu'iceux || prenants || leur cōmen- || cement & || origine de || l'vnité (de || touts nom- || bres source) || sans aucu- || nement se || desuoyer ou || decliner, ne || à dextre ne || à senestre || ainsi que || font les berlongs áutourdiceux trouuez: Mais tenants la voye || moyenne & rectitude diametrale, sont veus tomber en la cente- || naire vnité & d'icelle par le mesme chemin remontant, estre en || fin à l'indiuisible vnité reuocquez: Laquelle voye ilz ont voulu ap- || peller le chemin de vie... || ... || D'ou Aristoteles a prins occasion d'appel- || ler le quarré heureux sans vituperation.’ Op bladz. 87 geeft van der eycke het tafeltje.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 110]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
‘Mais encore peut on icy veoir, que cōme le contenu du quarre dont || le coste est 1. ainsi veult aussi le contenu du cercle dont le diametre faict || 1. estre representé, par le quart du nombre representant son circuit ou || sa circumference.’ Na het opgeven van eenige eigenschappen van gelijkvormige figuren, waarbij hij zijn gevonden verhouding gebruikt, om natuurlijk tot even onware uitkomsten te geraken, beweert hij (bladz. 89). ‘De laquelle proprieté (si- || bien on y prend garde) le cercle ne veult estre priué. Chose qui auec || les ja mentionnées nous peut asseurer cestedicte raison de 1521. || à 484. estre celle de la circumference à son diametre. Et pour- || ce aussi tant la circumference que le contenu du cercle vouloir estre || representer par nombres quarrez duquel le diametre ou la lōgueur || d'icelluy est par vn nombve quarré representê. Et le contenu du || cercle dont le diametre est vn nombre discible vouloir pareille- || ment estre representé par vn nombre quarré: Duquel (àsçavoir) || les quatre angles droicts sont (mais occultement) au centre, (l'espa- || ce à l'entour du centre vallant quatre angles droicts) ce que tou- || tesfois tu estimeras sans tresgrand mystere ne pouuoir ainsi estre.’ Hebben wij van deze beschouwingen omtrent de geheimzinnige eigenschappen en neigingen der getallen vroeger reeds meermalen voorbeelden ontmoet, onze schrijver eindigt met eene dergelijke peroratie, die in die dagen echter goede kans op algemeene bewondering aanbood. Hij zegt bladz. 89. ‘Mais encore à (sic) cestedicte raison 1521/484. cela en soy, à sçauoir || que si on adiouste touts ses superieurs nōbres ensemble comme pre- || miers, & semblablement ses inferiéurs nombres comme premiers, || on trouuera qu'ilz feront ces quarrez 9/16, dont les racines quarrées || ¾. sont les costez diametraux du premier nombre diametral 12. || Et adioustant iceuxdicts quarrez 9/16. ensemble, on les trouuera || faire 25. qui est le quarré de 5. premier nombre diametre. Et que || plus est si apres ainsi auoir rangé ces nombres 1521/484. 9/16. ¾. 25. on || adiouste les superieurs & inferieurs nombres de chascun apart soy || en- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 111]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
semble comme premiers, & ceux qui de telle addition seront || procréez encore ensemble comme premiers, continuant une telle || maniere d'adiouster, jusques à ce qu'il vienne par tout vn nombre || digite, on trouuera finalement des quatre nombres 7. 7. 7. 7. c'est || à dire 4. 4. 4. 4. 4. 4. 4. lesquels derechef ensemble adioustez, fe- || ront premierement 28. qui depuis l'vnité est le troisiesme en la || progression des nōbres parfaicts. Et en fin finale 1. qui est celluy par || lequel nous auons commencé ce probleme, & par lequel nous le || finirons. Rendant graces & louanges à l'Eternel, duquel toutes || choses procedent, & auquel toutes choses sont finalement || reuocquées, Par Jesus Christ son Filz vnic- || que nostre saulueur et redempteur || auec son sainct Esprit. || Amen. || Fin.’ || Brengt men de aangehaalde plaatsen met elkander in verband, dan ziet men, dat van der eycke eerst eene lijn construeert, waarvan de berekening aantoont, dat zij eene nauwere benadering geeft dan de verhouding van archimedes (zie blz. 73); maar daarna komt er hij er door zijne sophismen toe om aan te toonen, dat die verhouding noch grooter, noch kleiner kan wezen. 8. Voor dat wij afscheid nemen van dit zeldzame boekje, dat tot zooveel tegenspraak, en dientengevolge tot zoo gewichtige gevolgen en bespiegelingen aanleiding heeft gegeven, nog een paar opmerkingen. Onder aan bladz. 90 vindt men de ‘Errata’, 31 in getal, een bewijs dat er veel moeite is genomen voor het zuiver drukken van het werk. Op de volgende bladzijde (zonder pagineering) komt voor ‘Extraict dv Privilege. Messievrs les Estatz generaulx des Prouinces || vnies des Païs bas, Ont consenti & accordé à Simon du || Chesne de faire Imprimer esdictes prouinces, certain li- || ure Intitulé qvadratvre dv cercle, par tel || Imprimeur que bon luy semblera. Auec deffences à touts || aultres d'Imprimer ou faire Imprimer vendre ou distri- || buer ledict liure es Prouinces susdictes, soit en Latin, Fran- || çois, hault ou bas Allemand, sans le vouloir, congé ou || consentement dudict du Chesne, & ce pour le terme de || dix ans, à peine de confiscation des exemplaires & par- || dessus ce de cincquante Reaulx d'or, à employer le tiers || au prouffit de l'annonciateur, l'aultre tiers au proffit de || l'Officier, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 112]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
& le tiers restant au prouffit de la cause com- || mune. Faict à Delff, le xxjme de Feburier, 1584. || Par Ordonnance de Messieurs les || Estatz generaulx || M. d'Hennin. En daaronder staat in het hollandsch, zeker tot bevordering van het debiet, ‘Men vercooptse by Simon vander Eycke,’ een bewijs, dat dit zijn eigenlijke naam was, en de fransche of latijnsche vertaling daarvan daarentegen zijn naam in de geleerde wereld was, zooals toen dikwerf voorkwam. 9. Onder de tegenschriften, die er in het licht kwamen tegen deze quadratuur, komt vooral in aanmerking het ‘Kort Claar bewijsGa naar eind4) van ludolf van ceulen,’ waarover later nader. Hierop schreef van der eycke zijn ‘Claerder bevvijs’Ga naar eind5) in het jaar 1586. Hiertegen schrijft Ludolf van Ceulen weder zijn ‘Proefsteen en Claerder Wederleggingh’ in 1586Ga naar eind6): en uit dit boekje blijkt, dat het Claerder Bevvijs van vander Eycke door hem werd opgedragen aan ‘Schout, Burgemeesteren en Raadt der stadt Delft.’ In dit geschrift maakt hij nog wel melding van zijne oorspronkelijke verhouding 3 69/484 (zie bladzijde 24); maar hij vervangt deze door eene andere R.R. 5120-32, dat wil bij onze schrijfwijze zeggen √[√(5120)-32]. Zoo leest men op bladz. 3. ‘(Indien het bevvijs mach hieten segghe ick) ghenoech versekert sijnde (hoevvel syn proces, tot voorsz. dimentie dienstlic ende infalible schijnt, in der vvaerheydt om de extractie der Irrationale vvortelen die daer by gheschieden anders deceptible) de precijse proportie van de circumferentie des circkels tot sijnen diameter, tusschen dese termijnen 3 10/71 ende 3 10/70, van hem gheghenen, gheensins gheconstitueert te sijn. Maer de circumferencie haer precijse tot den diameter te houden als R.R. 320-8 tot 1.’ En evenzoo later op bladz. 27. ‘Waer dan oock finalicke door bekent wert, R.R. 5120-32, de precijse lengde van tvierendeel wt de circumferencie des voorghegheven Cirkels te zijnGa naar voetnoot*). Achtervolgende het welck voor- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 113]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
waer de proportie van den Diameter tot de circumferencie buyten de termijnen Archimedis wert kommen te vallen, ende meerder zijn dan van 3 1/7 tot 1.’ Hieruit ziet men dat van der eycke nu geheel op het dwaal-spoor is geraakt, en de verhouding van archimedes, als strijdig met deze tweede quadratuur, verwerpt; terwijl het juist dezelfde verhouding van archimedes was, die hem leidde bij zijne eerste quadratuur. Vandaar dan ook, dat hij hier in dit laatste boekje de oorspronkelijke quadratuur 1521:484 geheel op zijde schuift. Trouwens zijne tweede quadratuur schijnt hem bij het schrijven van zijn eerste boekje reeds bekend geweest te zijn. Immers de daar voorkomende R. 9000-R 16200000. komt met de waarde hiér R.R. 320-8 overeen, wanneer men aldaar slechts voor den straal des cirkels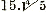 aanneemt. Beide waarden hebben den factor √{2(√5-1)}. aanneemt. Beide waarden hebben den factor √{2(√5-1)}.
‘Wanneer men beide waarden uitrekent, vindt men 1521:484 = 3.14256198, √(√5120-32) = 3.1446055. 10. Het is evenwel slechts de laatste waarde, die gewoonlijk als de quadratuur van simon van der eycke gegeven wordt: en hiervan is de oorzaak, dat men haar aantreft in het ‘Fundamentum Astronomicum’Ga naar eind7) van nicolaus raymarus ursus dithmarsus. Dit werk toch is vrij wat meer verbreid geworden dan de beide werkjes van simon van der eycke zelven. Deze arbeid behandelt eigenlijk eenige, een zevental, onderwerpen der sterrekunde, maar daarbij tevens eenige punten uit de meetkunde, die daarop betrekking hebben, de vervaardiging van sinustafels, de verdeeling van hoeken, de quadratuur des cirkels, en de driehoekmeting: hij is verdeeld in vijf hoofdstukken, waarvan het tweede handelt ‘de Extractione Canonis Sinuum’ en het derde ‘de doctrina triangulorum,’ de drie andere behandelen meer de toepassing der wiskunde op de sterrekunde. Deze schrijver had een vernuftig denkbeeld, waardoor hij de nakomelingschap zeer aan zich heeft verplicht: hij heeft toch de meeste der meetkundige figuren, die tusschen de tekst voorkomen, aan meer of minder bekende vrienden, tijdgenooten en geleerden, opgedragen; en daardoor eene niet onaardige bijdrage | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 114]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
geleverd voor de geschiedenis der wiskundige wetenschappen van die dagen. Meestal staat de figuur, of het daarbij behandelde onderwerp in eenig verband met den schrijver, wiens naarn daarnaast voorkomt: zoo is dit bij voorbeeld het geval met de figuur, toegewijd aan onzen simon van der eycke. Dit heeft nu plaats bij de volgende figuren.
terwijl de plaat is opgedragen aan ‘Principii Hassiae &c. Guilielmo. In het tweede hoofdstuk nu komt voor de verhandeling ‘de Quadratione Circuli.’ Hier begint hij, zoo als in dien tijd meer gebruikelijk was, met het geven van een overzicht zijner wijze van behandeling. Men vindt dit op de verso van bladzijde 9. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 115]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Daarop volgt, bladz. 10 recto, het meetkundig bewijs, maar zonder eenige berekening: men kan echter uit de figuur voor de verhouding tusschen de omtrek en achtmaal de straal, gemakkelijk afleiden het getal √(2{√8- 1}), zooals ons dit boven ook is voorgekomen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 116]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Niet alleen dat door het overnemen van van der eycke's quadratuur in dit grootere werk, die arbeid zeker meer bekend is geworden; maar ook heeft het middellijk verder gestrekt tot het onderwerp van een tegenschrift van adriaan van romen; en hierdoor weder zijn anders niet bekende bijzonderheden omtrent onzen ludolph van ceulen voor den dag gekomen, zooals ik hoop in een later nummer dezer Bouwstoffen mede te deelen. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||